湘教版(2024)七下第六章 综合与实践 学案
文档属性
| 名称 | 湘教版(2024)七下第六章 综合与实践 学案 |  | |
| 格式 | docx | ||
| 文件大小 | 769.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-22 17:38:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六章 收集、整理与描述数据
综合与实践——家乡变化情况的调查
学习目标与重难点
学习目标:
1.通过看美丽的家乡图片,让学生回忆自己家乡的一些变化,感受家乡的美.
2.通过调查家乡的变化,应用数学中的统计调查知识,感受统计调查在实际生活中的应用。
学习重点:家乡变化情况的调查制作.
学习难点:家乡变化情况的调查制作.
预习自测
一、单选题
1.2024年市有万名学生参加中考,为了了解这些考生的数学成绩,从中抽取200名考生的数学成绩进行统计分析,在这个问题中,下列说法:
①这万名考生的数学成绩是总体;
②每个考生是个体;
③200名考生是总体的一个样本;
④样本容量是200,
其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
2.为调查某中学学生对奥运会的了解程度,某课外活动小组进行了抽样调查,以下样本最具有代表性的是( )
A.九年级的全体学生 B.全校女生
C.全校每班学号尾号为5的学生 D.会打篮球的学生
3.若从甲、乙、丙、丁、戊五位老师中任选两位一起帮图书馆整理书籍,所需的时间如下表:如果选一个人单独去整理,花时间最少的是
合作方式 甲、乙 乙、丙 丙、丁 丁、戊 戊、甲
所需时间(h) 13 9 10 12 8
A.甲 B.戊 C.丁 D.丙
4.如图,七年一班学生参加社团活动,其中文学,科技,艺术三个社团的人数比为,若参加文学社团的学生有6人,则参加艺术社团的人数是( )
A.6人 B.7人 C.9人 D.14人
二、填空题
5.只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种调查方法叫做 .
抽样调查的几个组成部分:
要考察的全体对象称为 .
组成总体的每一个考察对象称为 .
被抽取的那些个体组成一个 .
样本中个体的数目称为 .
教学过程
一、创设情境、导入新课
看看美丽的家乡!
家乡有哪些变化呢,我们一起来探索吧。
二、合作交流、新知探究
探究:家乡变化情况的调查
教材第180页
说一说:
若需向外地客人介绍自己家乡近年的变化,可以从哪些方面进行介绍?
议一议:
若从经济方面的人均支出情况进行介绍,则可从食品、衣着、居住、生活用品及服务、交通通信、教育文化娱乐、医疗保健、其他用品及服务等方面进行调查吗?
与国家统计年鉴中“全国居民人均支出”的指标进行对比,看看你的调查要素是否符合国家统计要素.
想一想:
你认为只需调查一年的情况还是多调查几年的情况?可以调查家乡15年前的相应情况吗?如果要调查,会遇到哪些问题?有解决方案吗?
议一议
邀请本班 5~7 名同学组成调查小组,选择自己家附近的 2~3 个村或社区进行调查,如何选择才能保证调查结果具有代表性?
【强调】:收集数据常用的方法:
(1)民意调查:问卷调查、访问、投票……
(2)实地调查:现场观察……
(3)媒体调查:报纸、杂志、电视、互联网……
注意:1. 在收集数据的过程中,要根据实际情况选取合适的方法.
2. 选取收集数据的方法时,要掌握两个要点:一要简便易行;二要真实、全面.
做一做:
将调查得到的数据进行整理,并以合适的形式表示这些数据.
【强调】:整理收集的数据时,统计表的设计要合理;设计调查问卷时,不能存在选项中的内容有重叠现象、问题不容易回答或问题带有调查者的某种倾向等情况.
议一议:
与同学分析家乡变化的情况,思考还可从哪些角度介绍自己家乡的变化,并就如何加强哪些方面的建设可以使家乡发生更大变化提出建议.
由此,你经历了一个较为完整的统计过程,其流程如下:
做一做:
以 “家乡巨变” 为主题,制作一份宣传材料,展示给全校同学.
三、自主检测
一、填空题
1.指出下列调查是适合普查,还是适合抽样调查.
(1)调查全国中学生的环保意识: ;
(2)调查某市开发区合资企业的数量: .
二、解答题
2.某校为了解九年级学生对自己三年来所用的数学课本的看法,向120名同学进行问卷调查,并得到下表:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 48 45 24 3
(1)分别计算每一种意见的人数占调查人数的百分比;
(2)根据上述统计表中的数据分别绘制折线图和扇形图;
(3)说一说从(2)中绘制的图中读到的信息(写出一条即可).
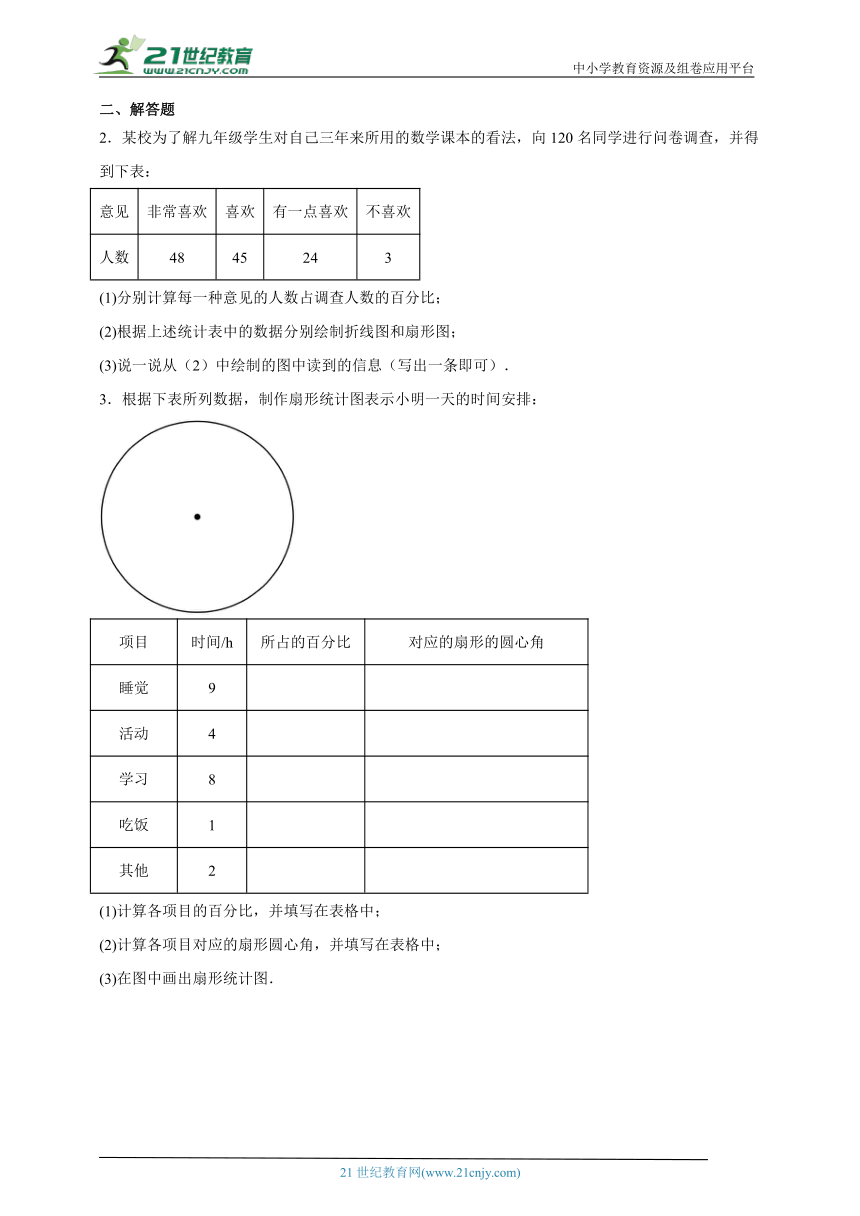
3.根据下表所列数据,制作扇形统计图表示小明一天的时间安排:
项目 时间/h 所占的百分比 对应的扇形的圆心角
睡觉 9
活动 4
学习 8
吃饭 1
其他 2
(1)计算各项目的百分比,并填写在表格中;
(2)计算各项目对应的扇形圆心角,并填写在表格中;
(3)在图中画出扇形统计图.
4.请指出下列抽样调查中的总体、个体、样本和样本容量
(1)为了解某所学校的学生参加课外体育活动的时间,调查了其中20名学生每天参加课外体育活动的时间;
(2)为了解某公园一年中平均每天进园的人数,对其中30天进园的人数进行了统计;
(3)为了解八年级学生的视力情况,学校从八年级随机抽取44名学生进行视力检查.
5.下列调查中,哪些适合做普查?哪些适合做抽样调查?
(1)了解你所在班级的同学对篮球运动的喜爱程度;
(2)了解《新闻联播》节目在青少年群体中的收视率;
(3)了解我校八年级学生平均每天完成家庭作业的时间;
(4)了解一批新能源汽车的电池质量.
四、知识点总结
答案
预习自测
1.C
【分析】本题考查总体、个体、样本、样本容量,理解总体、样本、样本容量的意义是正确解答的关键.
根据考查的对象是万名学生的中考数学成绩,利用总体、个体、样本、样本容量之间的关系进行判断即可.
【详解】解:这万名考生的数学成绩是总体,故①说法正确;
每个考生的数学成绩是个体,故②说法错误;
200名考生的数学成绩是总体的一个样本,故③说法错误;
样本容量是200故④说法正确;
所以,说法正确的有2个,
故选:C.
2.C
【分析】此题主要考查了抽样调查的可靠性,正确理解抽样调查的意义是解题关键.抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【详解】解:A、B、D中的进行的抽查,对抽查的对象划定了范围,不具备代表性,C抽查全校每班学号尾号为5的学生具有代表性;
故选C.
3.D
【分析】本题主要考查了实际问题的最值,解题时,利用了对比的方法进行解答.根据图中的数据通过两两对比进行分析解答.
【详解】解:根据甲、乙与乙、丙合作所需时间进行对比知,所需的时间是甲丙;
根据丙、丁与乙、丙合作所需时间进行对比知,所需的时间是丁乙;
根据丙、丁与丁、戊合作所需时间进行对比知,所需的时间是戊丙;
根据戊、甲与丁、戊合作所需时间进行对比知,所需的时间是丁甲;
根据甲、乙与戊、甲合作所需时间进行对比知,所需的时间是乙戊;
综上所述,所需时间的大小关系为:丁甲乙戊丙.
所以,花时间最少的是丙.
故选:D.
4.C
【分析】先求解总人数为人,再由总人数乘以参加艺术社团的人数的占比即可得到结论.
【详解】解:∵文学,科技,艺术三个社团的人数比为,参加文学社团的学生有6人,
∴总人数为:(人),
∴参加艺术社团的人数是为(人),
故选C
【点睛】本题考查的是扇形统计图,熟练的利用扇形图求解总量与某部分的数量是解本题的关键.
5. 抽样调查 总体 个体 样本 样本容量
自主检测
1. 抽样调查 普查
【分析】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查 无法进行全面调查 全面调查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.
【详解】解:(1)调查全国中学生的环保意识适合抽样调查,
故答案为:抽样调查;
(2)调查某市开发区合资企业的数量适合普查,
故答案为:普查.
2.(1)非常喜欢:;喜欢:;有一点喜欢:;不喜欢:
(2)见解析
(3)答案不唯一,见解析
【分析】本题考查了折线统计图和扇形统计图的绘制,读懂统计表的信息,求得每种情况所占百分比是解题的关键.
(1)根据题意利用每种意见的人数除以总人数即可求出答案;
(2)根据统计表中数据在图中找到相应的点,即可画出折线统计图,求得每种情况所占百分比即为相对应的圆心角,继而画出扇形统计图;
(3)根据折线图和扇形图,言之有理即可.
【详解】(1)解:非常喜欢:,
喜欢:,
有一点喜欢,
不喜欢;
(2)解:折线统计图如下:
非常喜欢所在圆心角度数为:,
喜欢所在圆心角度数为:,
有一点喜欢所在圆心角度数为:,
不喜欢所在圆心角度数为:,
绘制扇形统计图如下:
(3)解:九年级学生中“非常喜欢”自己三年来所用的数学课本的人数最多(言之有理即可).
3.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了作扇形统计图,求扇形统计图中各项的圆心角和百分比,解题的关键是数形结合熟练掌握扇形统计图的特点.
(1)用各项所用时间除以总时间求出百分比即可;
(2)用乘各项的百分比求出扇形圆心角即可;
(3)根据求出的百分比和扇形圆心角作出扇形统计图即可.
【详解】(1)解:睡觉所占的百分比为:;
活动所占的百分比为:;
学习所占的百分比为:;
吃饭所占的百分比为:;
其他所占的百分比为:.
(2)解:睡觉所对应的扇形圆心角:;
活动所对应的扇形圆心角:;
学习所对应的扇形圆心角:;
吃饭所对应的扇形圆心角:;
其他所对应的扇形圆心角:.
项目 时间/h 所占的百分比 对应的扇形的圆心角
睡觉 9
活动 4
学习 8
吃饭 1
其他 2
(3)解:画出扇形统计图,如图所示:
4.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了总体、个体、样本、样本容量的知识,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
(1)根据总体、个体、样本、样本容量的定义,进行判断即可;
(2)根据总体、个体、样本、样本容量的定义,进行判断即可;
(3)根据总体、个体、样本、样本容量的定义,进行判断即可.
【详解】(1)解:总体:该校学生参加课外体育活动的时间;
个体:每位学生参加课外体育活动的时间;
样本:20名学生每天参加课外体育活动的时间;
样本容量:20;
(2)解:总体:该公园一年中平均每天进园的人数;
个体:每天进园的人数;
样本:其中30天进园的人数;
样本容量:30;
(3)解:总体:八年级学生的视力情况;
个体:每个学生的视力情况;
样本:44名学生的视力情况;
样本容量:44.
5.(1)普查
(2)抽样调查
(3)普查
(4)抽样调查
【分析】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
(1)(2)(3)(4)根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答进行判断即可.
【详解】(1)解:了解你所在班级的同学对篮球运动的喜爱程度适合普查;
(2)解:了解《新闻联播》节目在青少年群体中的收视率适合抽样调查;
(3)解:了解我校八年级学生平均每天完成家庭作业的时间适合普查;
(4)解:了解一批新能源汽车的电池质量适合抽样调查.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 收集、整理与描述数据
综合与实践——家乡变化情况的调查
学习目标与重难点
学习目标:
1.通过看美丽的家乡图片,让学生回忆自己家乡的一些变化,感受家乡的美.
2.通过调查家乡的变化,应用数学中的统计调查知识,感受统计调查在实际生活中的应用。
学习重点:家乡变化情况的调查制作.
学习难点:家乡变化情况的调查制作.
预习自测
一、单选题
1.2024年市有万名学生参加中考,为了了解这些考生的数学成绩,从中抽取200名考生的数学成绩进行统计分析,在这个问题中,下列说法:
①这万名考生的数学成绩是总体;
②每个考生是个体;
③200名考生是总体的一个样本;
④样本容量是200,
其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
2.为调查某中学学生对奥运会的了解程度,某课外活动小组进行了抽样调查,以下样本最具有代表性的是( )
A.九年级的全体学生 B.全校女生
C.全校每班学号尾号为5的学生 D.会打篮球的学生
3.若从甲、乙、丙、丁、戊五位老师中任选两位一起帮图书馆整理书籍,所需的时间如下表:如果选一个人单独去整理,花时间最少的是
合作方式 甲、乙 乙、丙 丙、丁 丁、戊 戊、甲
所需时间(h) 13 9 10 12 8
A.甲 B.戊 C.丁 D.丙
4.如图,七年一班学生参加社团活动,其中文学,科技,艺术三个社团的人数比为,若参加文学社团的学生有6人,则参加艺术社团的人数是( )
A.6人 B.7人 C.9人 D.14人
二、填空题
5.只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种调查方法叫做 .
抽样调查的几个组成部分:
要考察的全体对象称为 .
组成总体的每一个考察对象称为 .
被抽取的那些个体组成一个 .
样本中个体的数目称为 .
教学过程
一、创设情境、导入新课
看看美丽的家乡!
家乡有哪些变化呢,我们一起来探索吧。
二、合作交流、新知探究
探究:家乡变化情况的调查
教材第180页
说一说:
若需向外地客人介绍自己家乡近年的变化,可以从哪些方面进行介绍?
议一议:
若从经济方面的人均支出情况进行介绍,则可从食品、衣着、居住、生活用品及服务、交通通信、教育文化娱乐、医疗保健、其他用品及服务等方面进行调查吗?
与国家统计年鉴中“全国居民人均支出”的指标进行对比,看看你的调查要素是否符合国家统计要素.
想一想:
你认为只需调查一年的情况还是多调查几年的情况?可以调查家乡15年前的相应情况吗?如果要调查,会遇到哪些问题?有解决方案吗?
议一议
邀请本班 5~7 名同学组成调查小组,选择自己家附近的 2~3 个村或社区进行调查,如何选择才能保证调查结果具有代表性?
【强调】:收集数据常用的方法:
(1)民意调查:问卷调查、访问、投票……
(2)实地调查:现场观察……
(3)媒体调查:报纸、杂志、电视、互联网……
注意:1. 在收集数据的过程中,要根据实际情况选取合适的方法.
2. 选取收集数据的方法时,要掌握两个要点:一要简便易行;二要真实、全面.
做一做:
将调查得到的数据进行整理,并以合适的形式表示这些数据.
【强调】:整理收集的数据时,统计表的设计要合理;设计调查问卷时,不能存在选项中的内容有重叠现象、问题不容易回答或问题带有调查者的某种倾向等情况.
议一议:
与同学分析家乡变化的情况,思考还可从哪些角度介绍自己家乡的变化,并就如何加强哪些方面的建设可以使家乡发生更大变化提出建议.
由此,你经历了一个较为完整的统计过程,其流程如下:
做一做:
以 “家乡巨变” 为主题,制作一份宣传材料,展示给全校同学.
三、自主检测
一、填空题
1.指出下列调查是适合普查,还是适合抽样调查.
(1)调查全国中学生的环保意识: ;
(2)调查某市开发区合资企业的数量: .
二、解答题
2.某校为了解九年级学生对自己三年来所用的数学课本的看法,向120名同学进行问卷调查,并得到下表:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 48 45 24 3
(1)分别计算每一种意见的人数占调查人数的百分比;
(2)根据上述统计表中的数据分别绘制折线图和扇形图;
(3)说一说从(2)中绘制的图中读到的信息(写出一条即可).
3.根据下表所列数据,制作扇形统计图表示小明一天的时间安排:
项目 时间/h 所占的百分比 对应的扇形的圆心角
睡觉 9
活动 4
学习 8
吃饭 1
其他 2
(1)计算各项目的百分比,并填写在表格中;
(2)计算各项目对应的扇形圆心角,并填写在表格中;
(3)在图中画出扇形统计图.
4.请指出下列抽样调查中的总体、个体、样本和样本容量
(1)为了解某所学校的学生参加课外体育活动的时间,调查了其中20名学生每天参加课外体育活动的时间;
(2)为了解某公园一年中平均每天进园的人数,对其中30天进园的人数进行了统计;
(3)为了解八年级学生的视力情况,学校从八年级随机抽取44名学生进行视力检查.
5.下列调查中,哪些适合做普查?哪些适合做抽样调查?
(1)了解你所在班级的同学对篮球运动的喜爱程度;
(2)了解《新闻联播》节目在青少年群体中的收视率;
(3)了解我校八年级学生平均每天完成家庭作业的时间;
(4)了解一批新能源汽车的电池质量.
四、知识点总结
答案
预习自测
1.C
【分析】本题考查总体、个体、样本、样本容量,理解总体、样本、样本容量的意义是正确解答的关键.
根据考查的对象是万名学生的中考数学成绩,利用总体、个体、样本、样本容量之间的关系进行判断即可.
【详解】解:这万名考生的数学成绩是总体,故①说法正确;
每个考生的数学成绩是个体,故②说法错误;
200名考生的数学成绩是总体的一个样本,故③说法错误;
样本容量是200故④说法正确;
所以,说法正确的有2个,
故选:C.
2.C
【分析】此题主要考查了抽样调查的可靠性,正确理解抽样调查的意义是解题关键.抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【详解】解:A、B、D中的进行的抽查,对抽查的对象划定了范围,不具备代表性,C抽查全校每班学号尾号为5的学生具有代表性;
故选C.
3.D
【分析】本题主要考查了实际问题的最值,解题时,利用了对比的方法进行解答.根据图中的数据通过两两对比进行分析解答.
【详解】解:根据甲、乙与乙、丙合作所需时间进行对比知,所需的时间是甲丙;
根据丙、丁与乙、丙合作所需时间进行对比知,所需的时间是丁乙;
根据丙、丁与丁、戊合作所需时间进行对比知,所需的时间是戊丙;
根据戊、甲与丁、戊合作所需时间进行对比知,所需的时间是丁甲;
根据甲、乙与戊、甲合作所需时间进行对比知,所需的时间是乙戊;
综上所述,所需时间的大小关系为:丁甲乙戊丙.
所以,花时间最少的是丙.
故选:D.
4.C
【分析】先求解总人数为人,再由总人数乘以参加艺术社团的人数的占比即可得到结论.
【详解】解:∵文学,科技,艺术三个社团的人数比为,参加文学社团的学生有6人,
∴总人数为:(人),
∴参加艺术社团的人数是为(人),
故选C
【点睛】本题考查的是扇形统计图,熟练的利用扇形图求解总量与某部分的数量是解本题的关键.
5. 抽样调查 总体 个体 样本 样本容量
自主检测
1. 抽样调查 普查
【分析】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查 无法进行全面调查 全面调查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.
【详解】解:(1)调查全国中学生的环保意识适合抽样调查,
故答案为:抽样调查;
(2)调查某市开发区合资企业的数量适合普查,
故答案为:普查.
2.(1)非常喜欢:;喜欢:;有一点喜欢:;不喜欢:
(2)见解析
(3)答案不唯一,见解析
【分析】本题考查了折线统计图和扇形统计图的绘制,读懂统计表的信息,求得每种情况所占百分比是解题的关键.
(1)根据题意利用每种意见的人数除以总人数即可求出答案;
(2)根据统计表中数据在图中找到相应的点,即可画出折线统计图,求得每种情况所占百分比即为相对应的圆心角,继而画出扇形统计图;
(3)根据折线图和扇形图,言之有理即可.
【详解】(1)解:非常喜欢:,
喜欢:,
有一点喜欢,
不喜欢;
(2)解:折线统计图如下:
非常喜欢所在圆心角度数为:,
喜欢所在圆心角度数为:,
有一点喜欢所在圆心角度数为:,
不喜欢所在圆心角度数为:,
绘制扇形统计图如下:
(3)解:九年级学生中“非常喜欢”自己三年来所用的数学课本的人数最多(言之有理即可).
3.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了作扇形统计图,求扇形统计图中各项的圆心角和百分比,解题的关键是数形结合熟练掌握扇形统计图的特点.
(1)用各项所用时间除以总时间求出百分比即可;
(2)用乘各项的百分比求出扇形圆心角即可;
(3)根据求出的百分比和扇形圆心角作出扇形统计图即可.
【详解】(1)解:睡觉所占的百分比为:;
活动所占的百分比为:;
学习所占的百分比为:;
吃饭所占的百分比为:;
其他所占的百分比为:.
(2)解:睡觉所对应的扇形圆心角:;
活动所对应的扇形圆心角:;
学习所对应的扇形圆心角:;
吃饭所对应的扇形圆心角:;
其他所对应的扇形圆心角:.
项目 时间/h 所占的百分比 对应的扇形的圆心角
睡觉 9
活动 4
学习 8
吃饭 1
其他 2
(3)解:画出扇形统计图,如图所示:
4.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了总体、个体、样本、样本容量的知识,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
(1)根据总体、个体、样本、样本容量的定义,进行判断即可;
(2)根据总体、个体、样本、样本容量的定义,进行判断即可;
(3)根据总体、个体、样本、样本容量的定义,进行判断即可.
【详解】(1)解:总体:该校学生参加课外体育活动的时间;
个体:每位学生参加课外体育活动的时间;
样本:20名学生每天参加课外体育活动的时间;
样本容量:20;
(2)解:总体:该公园一年中平均每天进园的人数;
个体:每天进园的人数;
样本:其中30天进园的人数;
样本容量:30;
(3)解:总体:八年级学生的视力情况;
个体:每个学生的视力情况;
样本:44名学生的视力情况;
样本容量:44.
5.(1)普查
(2)抽样调查
(3)普查
(4)抽样调查
【分析】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
(1)(2)(3)(4)根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答进行判断即可.
【详解】(1)解:了解你所在班级的同学对篮球运动的喜爱程度适合普查;
(2)解:了解《新闻联播》节目在青少年群体中的收视率适合抽样调查;
(3)解:了解我校八年级学生平均每天完成家庭作业的时间适合普查;
(4)解:了解一批新能源汽车的电池质量适合抽样调查.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
