新正弦定理
图片预览

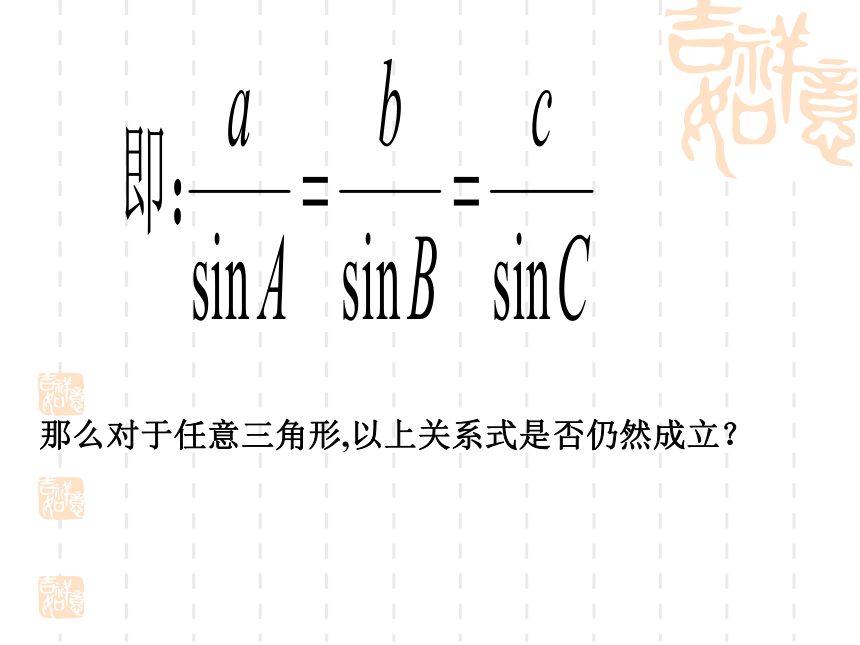



文档简介
课件12张PPT。数学必修51.1.1 正弦定理
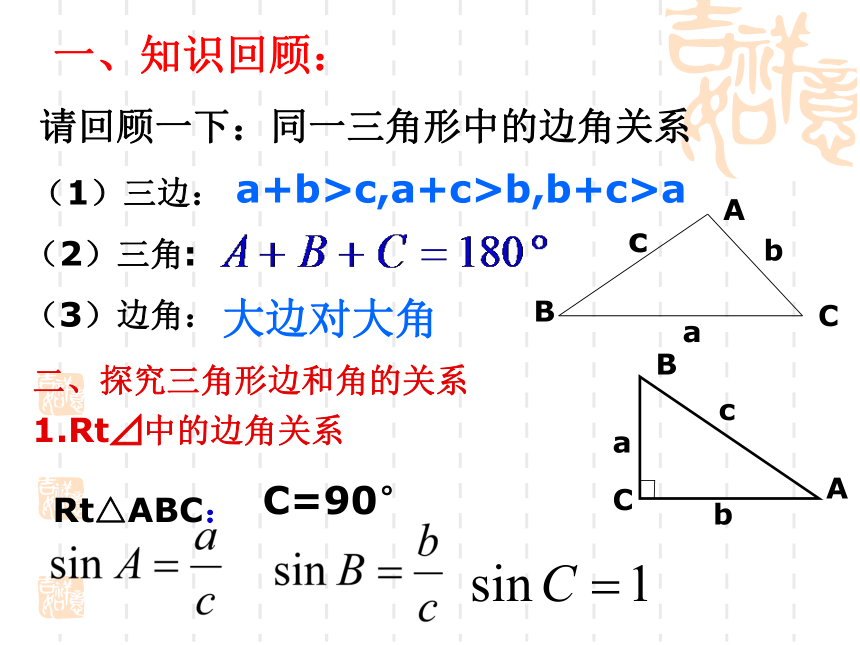
芦瑜利 高二142班请回顾一下:同一三角形中的边角关系一、知识回顾:a+b>c,a+c>b,b+c>a(1)三边:(2)三角:(3)边角:大边对大角二、探究三角形边和角的关系
1.Rt⊿中的边角关系
Rt△ABC:C=90°那么对于任意三角形,以上关系式是否仍然成立?所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有 2.若三角形是锐角三角形, 如图1,3.对于钝角三角形,以上等式还成立吗?等同学自己证明?三.新课讲解
新定义一:
(1)正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点:对称美 简洁美(3)方程的观点正弦定理实际上是已知其中三个,求另一个. 新 定义二:把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形。解三角形就是:由已知的边和角,求未知的边和角。例1.已知在ΔABC中,c=10,A=450,C=300,求a,b和B 解:∵c=10 A=450,C=300
∴B= 1800 -(A+C)=1050 由 = 得 a= = =10由 =
得 b= = = 20sin1050=20×
= 5 +5四.例题讲解:例2 已知a=16,b= , A=30° .解三角形
解:由正弦定理得所以B=60°,或B=120°C=90°C=30°当B=120°时五学生练习结束1、在 ,一定成立的等式是( ) 3、在△ABC中 已知a=18,B=60°,C=45°,求b= 2、已知c= 1,A=45°,B=30°,则 a=____,接下来有点难哦,加油!4、△ABC中,B=30°,c=150,b=50 ,则△ABC的形状是( )
5、已知c=2,A=120°,a= ,则B=____六、小结1.这节课我们主要学习了正弦定理,以及应用正弦定理解决的两类解三角形问题:
1)已知两角及一边求其他元素。
2)已知两边及一边对角求其他元素。
2.通过本节课学习,在研究数学问题时要掌握从特殊到一般、数形结合、分类讨论、化归转化的数学思想.再见衷心感谢各位老师的光临指导
芦瑜利 高二142班请回顾一下:同一三角形中的边角关系一、知识回顾:a+b>c,a+c>b,b+c>a(1)三边:(2)三角:(3)边角:大边对大角二、探究三角形边和角的关系
1.Rt⊿中的边角关系
Rt△ABC:C=90°那么对于任意三角形,以上关系式是否仍然成立?所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有 2.若三角形是锐角三角形, 如图1,3.对于钝角三角形,以上等式还成立吗?等同学自己证明?三.新课讲解
新定义一:
(1)正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点:对称美 简洁美(3)方程的观点正弦定理实际上是已知其中三个,求另一个. 新 定义二:把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形。解三角形就是:由已知的边和角,求未知的边和角。例1.已知在ΔABC中,c=10,A=450,C=300,求a,b和B 解:∵c=10 A=450,C=300
∴B= 1800 -(A+C)=1050 由 = 得 a= = =10由 =
得 b= = = 20sin1050=20×
= 5 +5四.例题讲解:例2 已知a=16,b= , A=30° .解三角形
解:由正弦定理得所以B=60°,或B=120°C=90°C=30°当B=120°时五学生练习结束1、在 ,一定成立的等式是( ) 3、在△ABC中 已知a=18,B=60°,C=45°,求b= 2、已知c= 1,A=45°,B=30°,则 a=____,接下来有点难哦,加油!4、△ABC中,B=30°,c=150,b=50 ,则△ABC的形状是( )
5、已知c=2,A=120°,a= ,则B=____六、小结1.这节课我们主要学习了正弦定理,以及应用正弦定理解决的两类解三角形问题:
1)已知两角及一边求其他元素。
2)已知两边及一边对角求其他元素。
2.通过本节课学习,在研究数学问题时要掌握从特殊到一般、数形结合、分类讨论、化归转化的数学思想.再见衷心感谢各位老师的光临指导
