10.1.1 全等三角形的判定(含答案)
文档属性
| 名称 | 10.1.1 全等三角形的判定(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 386.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-23 15:26:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
1 全等三角形
第1课时 全等三角形的判定
基础闯关
知识点一:全等三角形的判定方法
方法1:利用“SSS”判定三角形全等
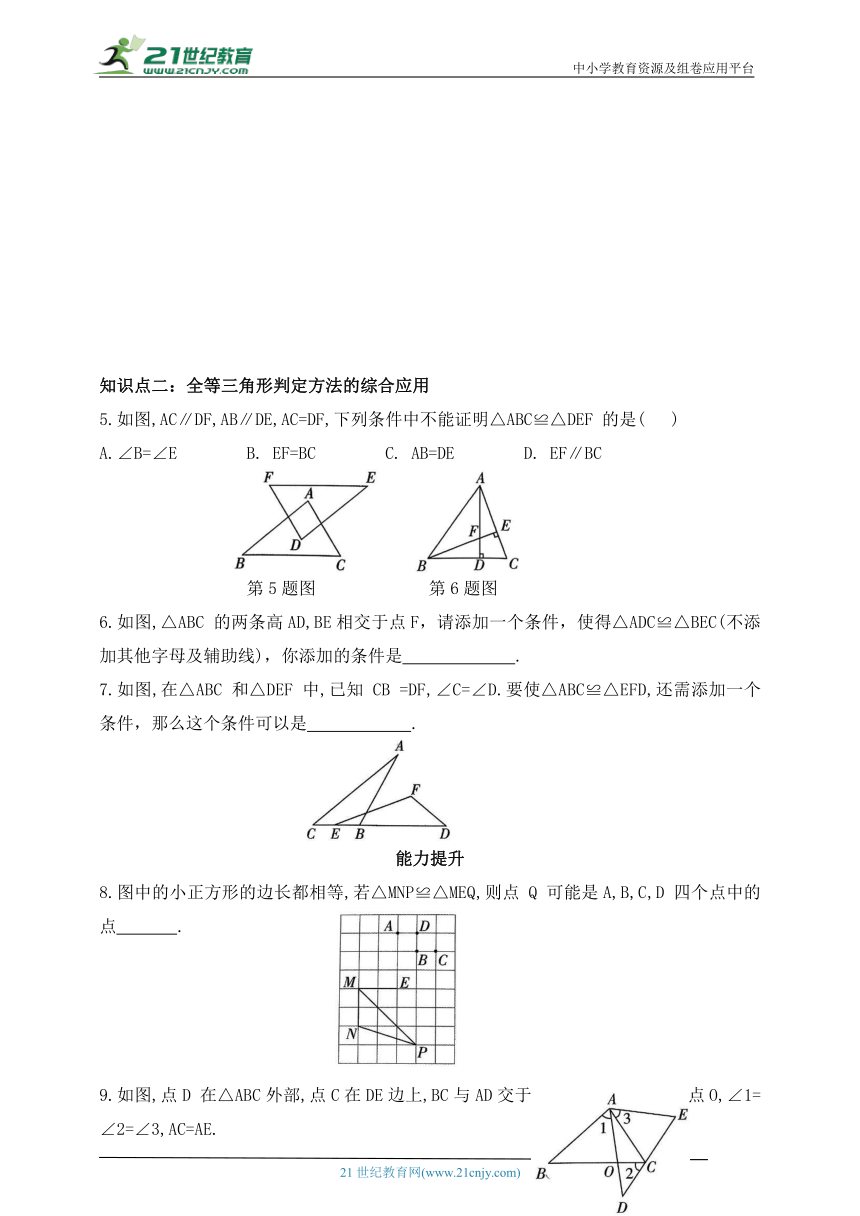
1.用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是( )
A. SSS B. SAS C. ASA D. AAS
方法2:利用“AAS”判定三角形全等
2.如图,BC=EF,根据已知条件能够直接判定△ABC≌△DEF 的依据是( )
A. AAS B. SAS C. ASA D. SSS
方法3:利用“SAS”判定三角形全等
3.如图,在△ABC 和△ADE 中,延长BC 交DE 于点F,BC=DE,AC=AE,∠ACF+∠AED=180°.求证:AB=AD.
方法 4:利用“ASA”判定三角形全等
4.如图,在四边形ABCD 中,AD∥BC,点 M 为对角线 AC 上一点,连接 BM,AC=BC,∠AMB=∠BCD.求证:△ADC≌△CMB.
知识点二:全等三角形判定方法的综合应用
5.如图,AC∥DF,AB∥DE,AC=DF,下列条件中不能证明△ABC≌△DEF 的是( )
A.∠B=∠E B. EF=BC C. AB=DE D. EF∥BC
第5题图 第6题图
6.如图,△ABC 的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是 .
7.如图,在△ABC 和△DEF 中,已知 CB =DF,∠C=∠D.要使△ABC≌△EFD,还需添加一个条件,那么这个条件可以是 .
能力提升
8.图中的小正方形的边长都相等,若△MNP≌△MEQ,则点 Q 可能是A,B,C,D 四个点中的点 .
9.如图,点D 在△ABC外部,点C在DE边上,BC与AD交于点O,∠1=∠2=∠3,AC=AE.
(1)求证:∠B=∠D.
(2)求证:△ABC≌△ADE.
10.如图,在△ABC中,点D在BC上,AD平分∠BAC,点E,F分别在AC,AB上,满足AE=BF,DE∥AB.
(1)求证:∠DAE=∠ADE.
(2)判断△BFD 与△EDF 是否全等,并说明理由.
11.长方形具有四个内角均为直角,两组对边分别平行且相等的特征.如图,把一张长方形纸片ABCD 折叠,使点 C 与点 A 重合,折痕为EF.
(1)如果∠DEF=120°,求∠BAF 的度数.
(2)判断△ABF 和△AGE 是否全等,请说明理由.
参考答案
1. A 2. A
3.证明:∵∠ACB +∠ACF =∠ACF+∠AED=180°,∴∠ACB = ∠AED.
在 △ABC 和 △ADE 中,,∴△ABC≌△ADBE(SAS),∴AB=AD.
4.证明:∵AD∥BC,∴∠DAC=∠MCB.
∵∠AMB =∠BCD,∠CBM+∠ACB=∠AMB,∠ACB+∠ACD=∠BCD,∴∠CBM=∠ACD.
在△ADC 和△CMB 中,∵∴△ADC≌△CMB(ASA).
5. B
6.示例:AC=BC
7.示例:AC=ED
8. D
9.证明:(1)∵∠1=∠2,∠AOB=∠COD,∴∠B=∠D.
(2)∵∠1=∠3,∴∠1+∠DAC=∠3+∠DAC,即∠BAC=∠DAE.
在△ABC 与△ADE 中,∵∴△ABC≌△ADE(AAS).
10.(1)证明:如图,∵AD 平分∠BAC,∴∠1=∠2.
∵DE∥AB,∴∠2=∠3,∴∠1=∠3,即∠DAE=∠ADE.
(2)解:△BFD 与△EDF 全等.理由:由(1)知,∠DAE=∠ADE,则AE=DE.
又∵AE=BF,∴BF=DE.
∵DE∥AB,∴∠BFD=∠EDF.
在△BFD 与△EDF中,∵∴△BFD≌△EDF(SAS).
11.解:(1)∵四边形ABCD 是长方形,∴AD∥BC,∴∠CFE
由折叠知,∠AFE=∠CFE=60°,∴∠AFB=180°-∠AFE-∠CFE=60°.
∵∠B=90°,∴∠BAF=90°-∠AFB=30°.
(2)△ABF≌△AGE.理由:由折叠知,AG=CD,∠G=∠D=90°,∠GAF=∠C=90°.
∵∠B=90°,∴∠B=∠G.
∵AB=CD,∴AB=AG.
∵∠BAD=90°,∠GAF=90°,∴∠BAF=∠BAD-∠EAF=∠GAF-∠EAF=∠GAE.
在△ABF 和△AGE 中, (ASA).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
1 全等三角形
第1课时 全等三角形的判定
基础闯关
知识点一:全等三角形的判定方法
方法1:利用“SSS”判定三角形全等
1.用直尺和圆规作一个角等于已知角的作图痕迹如图所示,则作图的依据是( )
A. SSS B. SAS C. ASA D. AAS
方法2:利用“AAS”判定三角形全等
2.如图,BC=EF,根据已知条件能够直接判定△ABC≌△DEF 的依据是( )
A. AAS B. SAS C. ASA D. SSS
方法3:利用“SAS”判定三角形全等
3.如图,在△ABC 和△ADE 中,延长BC 交DE 于点F,BC=DE,AC=AE,∠ACF+∠AED=180°.求证:AB=AD.
方法 4:利用“ASA”判定三角形全等
4.如图,在四边形ABCD 中,AD∥BC,点 M 为对角线 AC 上一点,连接 BM,AC=BC,∠AMB=∠BCD.求证:△ADC≌△CMB.
知识点二:全等三角形判定方法的综合应用
5.如图,AC∥DF,AB∥DE,AC=DF,下列条件中不能证明△ABC≌△DEF 的是( )
A.∠B=∠E B. EF=BC C. AB=DE D. EF∥BC
第5题图 第6题图
6.如图,△ABC 的两条高AD,BE相交于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是 .
7.如图,在△ABC 和△DEF 中,已知 CB =DF,∠C=∠D.要使△ABC≌△EFD,还需添加一个条件,那么这个条件可以是 .
能力提升
8.图中的小正方形的边长都相等,若△MNP≌△MEQ,则点 Q 可能是A,B,C,D 四个点中的点 .
9.如图,点D 在△ABC外部,点C在DE边上,BC与AD交于点O,∠1=∠2=∠3,AC=AE.
(1)求证:∠B=∠D.
(2)求证:△ABC≌△ADE.
10.如图,在△ABC中,点D在BC上,AD平分∠BAC,点E,F分别在AC,AB上,满足AE=BF,DE∥AB.
(1)求证:∠DAE=∠ADE.
(2)判断△BFD 与△EDF 是否全等,并说明理由.
11.长方形具有四个内角均为直角,两组对边分别平行且相等的特征.如图,把一张长方形纸片ABCD 折叠,使点 C 与点 A 重合,折痕为EF.
(1)如果∠DEF=120°,求∠BAF 的度数.
(2)判断△ABF 和△AGE 是否全等,请说明理由.
参考答案
1. A 2. A
3.证明:∵∠ACB +∠ACF =∠ACF+∠AED=180°,∴∠ACB = ∠AED.
在 △ABC 和 △ADE 中,,∴△ABC≌△ADBE(SAS),∴AB=AD.
4.证明:∵AD∥BC,∴∠DAC=∠MCB.
∵∠AMB =∠BCD,∠CBM+∠ACB=∠AMB,∠ACB+∠ACD=∠BCD,∴∠CBM=∠ACD.
在△ADC 和△CMB 中,∵∴△ADC≌△CMB(ASA).
5. B
6.示例:AC=BC
7.示例:AC=ED
8. D
9.证明:(1)∵∠1=∠2,∠AOB=∠COD,∴∠B=∠D.
(2)∵∠1=∠3,∴∠1+∠DAC=∠3+∠DAC,即∠BAC=∠DAE.
在△ABC 与△ADE 中,∵∴△ABC≌△ADE(AAS).
10.(1)证明:如图,∵AD 平分∠BAC,∴∠1=∠2.
∵DE∥AB,∴∠2=∠3,∴∠1=∠3,即∠DAE=∠ADE.
(2)解:△BFD 与△EDF 全等.理由:由(1)知,∠DAE=∠ADE,则AE=DE.
又∵AE=BF,∴BF=DE.
∵DE∥AB,∴∠BFD=∠EDF.
在△BFD 与△EDF中,∵∴△BFD≌△EDF(SAS).
11.解:(1)∵四边形ABCD 是长方形,∴AD∥BC,∴∠CFE
由折叠知,∠AFE=∠CFE=60°,∴∠AFB=180°-∠AFE-∠CFE=60°.
∵∠B=90°,∴∠BAF=90°-∠AFB=30°.
(2)△ABF≌△AGE.理由:由折叠知,AG=CD,∠G=∠D=90°,∠GAF=∠C=90°.
∵∠B=90°,∴∠B=∠G.
∵AB=CD,∴AB=AG.
∵∠BAD=90°,∠GAF=90°,∴∠BAF=∠BAD-∠EAF=∠GAF-∠EAF=∠GAE.
在△ABF 和△AGE 中, (ASA).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
