10.2.3 等边三角形（含答案）

中小学教育资源及组卷应用平台
第十章 三角形的有关证明
2 等腰三角形
第3课时 等边三角形
基础闯关
知识点一：等边三角形的性质
1.如图,AD 是等边三角形ABC 的中线,AE=AD,则∠EDC=( )
A.30° B.20° C.25° D.15°
第1题图 第2题图
2.如图,等边三角形ABC 中,AD⊥BC,垂足为点D,点E 在线段 AD 上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
3.如图,∠MON=90°,以点O 为圆心，任意长为半径画弧，分别交OM，ON 于点A，D，再以点 A 为圆心，AO 长为半径画弧,与弧AD 交于点B,连接OB,AB,AB 的延长线交ON 于点C.若OD=4,则CB 的长为( )
A.3 B.4 C.5 D.6
第3题图 第4题图
4.如图,已知△ABC 是等边三角形,点 B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E= °.
知识点二：等边三角形的判定
5.[应用意识]由于木质衣架没有柔性，在挂置衣服的时候不太方便操作.小敏设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可.如图①,衣架杆OA=OB=18cm.若衣架收拢时,∠AOB=60°,如图②,则此时A，B两点之间的距离是 cm.
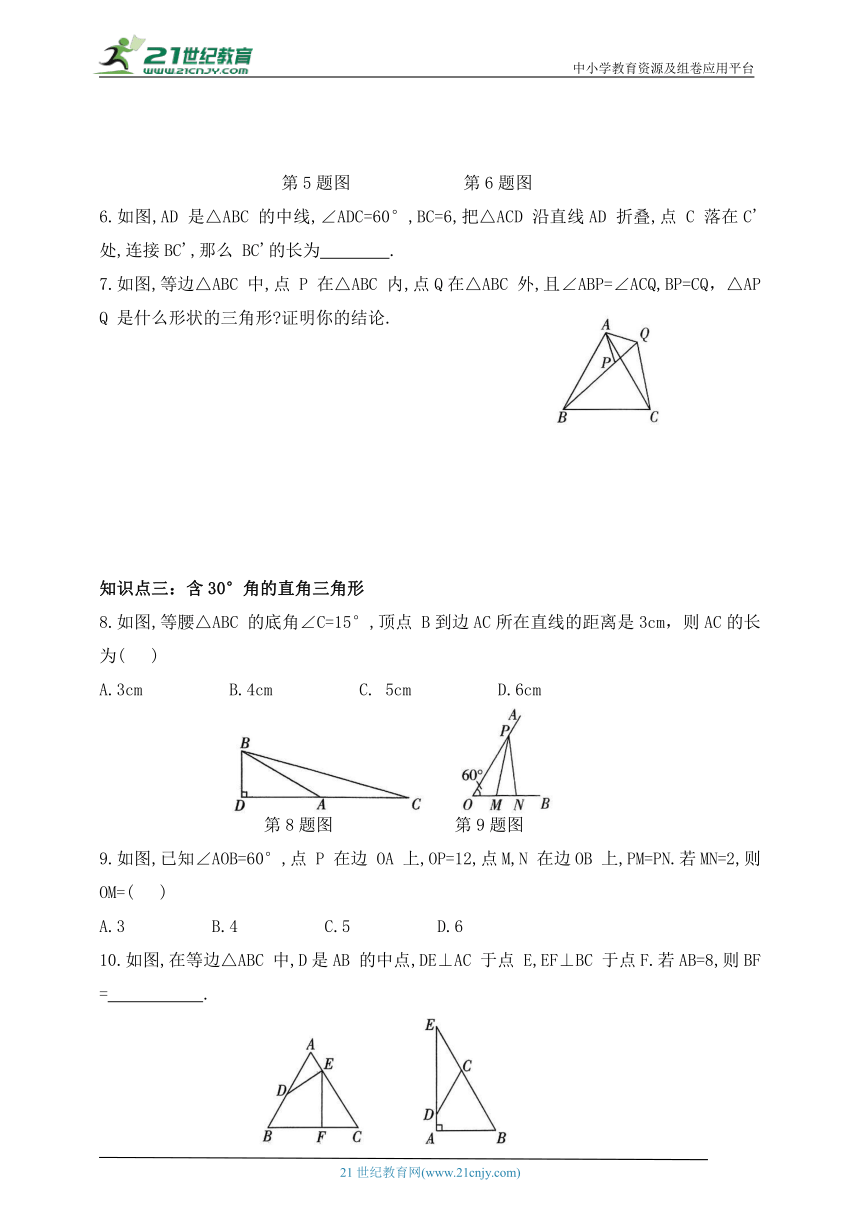
第5题图 第6题图
6.如图,AD 是△ABC 的中线,∠ADC=60°,BC=6,把△ACD 沿直线AD 折叠,点 C 落在C'处,连接BC',那么 BC'的长为 .
7.如图,等边△ABC 中,点 P 在△ABC 内,点Q在△ABC 外,且∠ABP=∠ACQ,BP=CQ，△APQ 是什么形状的三角形 证明你的结论.
知识点三：含30°角的直角三角形
8.如图,等腰△ABC 的底角∠C=15°,顶点 B到边AC所在直线的距离是3cm，则AC的长为( )
A.3cm B.4cm C. 5cm D.6cm
第8题图 第9题图
9.如图,已知∠AOB=60°,点 P 在边 OA 上,OP=12,点M,N 在边OB 上,PM=PN.若MN=2,则OM=( )
A.3 B.4 C.5 D.6
10.如图,在等边△ABC 中,D是AB 的中点,DE⊥AC 于点 E,EF⊥BC 于点F.若AB=8,则BF= .
第10题图 第11题图
11.如图,已知 Rt△ABE 中,∠A=90°,∠B=60°,BE=10,D 是线段AE 上的一动点,过点D 作CD交BE 于点C,并使得∠CDE=30°，则CD 长度的取值范围是 .
能力提升
素养提升微专题
【数学思想在等边三角形中的应用】
思想1：整体思想
12.三个等边三角形的摆放位置如图，若∠3=60°,则∠1+∠2的度数为( )
A.90° B.120° C.270° D.360°
思想2：分类讨论思想
13.在△ABC中,AB=AC,如果AB 边上的高等于AB 的一半，那么∠A 的度数是 .
14.如图，在等边三角形ABC中,D 为AC 边的中点,E为BC 边延长线上的一点，CE=CD,DM⊥BC于点M.下列结论正确的是 .(填序号)
①BM=3CM ②BM=EM ④DM=2CM
15.如图，D是等边三角形ABC 内一点,且 DB = DA,BP = AB,∠DBP=∠DAC.
(1)求证:∠ADB=∠PDC.
(2)求∠P 的度数.
16.如图，过等边△ABC 的顶点A,B,C 依次作AB,BC,AC 的垂线MG,MN,NG,三条垂线围成△MNG.若AM=2,求△MNG 的周长.
参考答案
1. D 2. A
3. B [解析]由作图可知:OA=OB=OD=4,OA=AB,
∴△ABO为等边三角形,∴∠OAC=∠ABO=∠AOB=60°.
∵∠MON=90°,∴∠BCO=∠BOC=30°,∴CB=OB=4.
4.15 5.18 6.3
7.解:△APQ是等边三角形.
证明:∵△ABC 是等边三角形,∴AB=AC.
在△ABP 与△ACQ 中,∵ ∴△ABP ≌△ACQ(SAS),
∴ AP = AQ,∠BAP =∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
8. D 9. C
10.5 [解析]∵在等边△ABC中,D是AB 的中点,AB=8,
∴AD=4,AC=BC=8,∠A=∠C=60°.
∵DE⊥AC于点E,EF⊥BC于点F,∴∠AED=∠CFE=90°,∠ADE
∴CF= CE=3,∴BF=8-3=5.
11.0＜CD≤5
12. B [解析]如图,∵图中是三个等边三角形,∠3=60°,
∵∠ABC+∠ACB+∠BAC=180°,∴60°+(120°-∠2)+(120°-∠1)=180°,
∴∠1+∠2=120°.
13.30°或150° [解析]分两种情况:
(1)如图①,∵AB=AC,
∵CD 为AB 边上的高,∴∠ADC=90°,∴∠A=30°.
(2)如图②,此时∠DAC=
综上,∠BAC 的度数为30°或150°.
14.①②③
15.(1)证明:∵△ABC 是等边三角形,∴AB=AC.
∵BP=AB,∴BP =AC.
又∵DB=DA,∠DBP =∠DAC,∴△BDP ≌△ADC (SAS),
∴ ∠ADC = ∠BDP,∴∠ADB=∠PDC.
(2)解:∵△ABC 是等边三角形,∴AB=AC,∠ACB=60°.
∵AC=BC,AD=BD,CD=CD,∴△ADC≌△BDC(SSS),∴∠ACD=∠BCD.
∵∠ACD+∠BCD=∠ACB=60°,∴∠BCD=∠ACD
由(1)知,△BDP≌△ADC,∴∠P =∠ACD
16.解:∵△ABC 为等边三角形,∴AB=AC,∠BAC=∠ABC= 60°.
∵AC⊥GN,BA⊥MG,CB⊥MN,∴∠ACG=∠BAM=∠CBM=90°,
∴∠CAG=90°-∠BAC=30°,∠ABM=90°-∠ABC=30°,∴△ABM≌△CAG(ASA),
∴MA=CG=2,即MG=AM+AG=CG+AG.
∵∠ABM=30°,∴∠M=90°-∠ABM=60°.
同理可得∠N=∠G=60°,∴△MNG 为等边三角形.
∵∠CAG=30°,∴AG=2CG=4.∵MG=CG+AG=6,∴△MNG 的周长=3MG=3×6=18.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)