第十章 三角形的有关证明 章末复习(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明 章末复习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 485.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-23 15:29:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
章末复习
考点整合
考点一:全等三角形的性质与判定
1.下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
2.如图,点 B,F,C,E 共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF 的是( )
A. AB=DE B.∠A=∠D C. AC=DF D. AC∥FD
第2题图 第3题图
3.如图,在正方形ABCD中,如果AF=BE,那么∠AOD 的度数是 .
4.在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
5.如图,点O 是线段AB 的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC.
(2)若∠ADO=35°,求∠DOC 的度数.
考点二:等腰(边)三角形的性质与判定
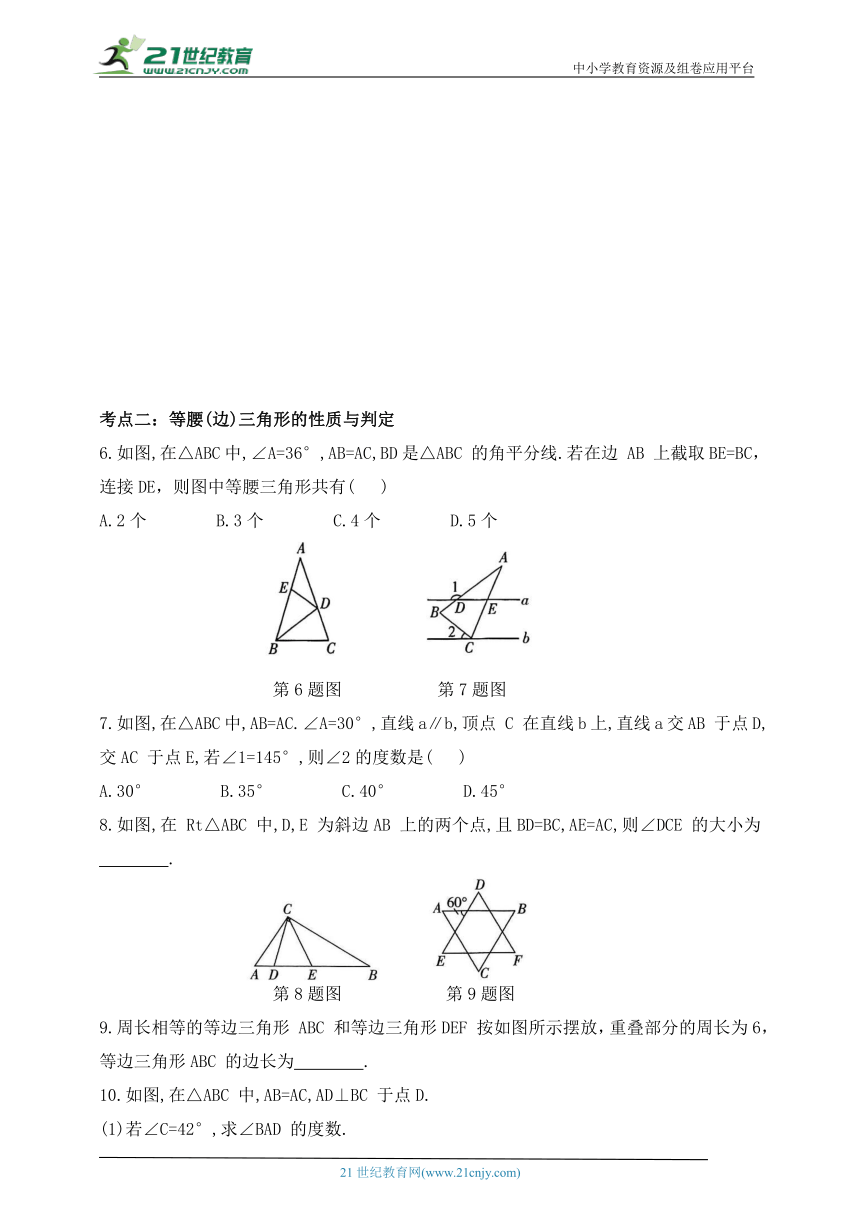
6.如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC 的角平分线.若在边 AB 上截取BE=BC,连接DE,则图中等腰三角形共有( )
A.2个 B.3个 C.4个 D.5个
第6题图 第7题图
7.如图,在△ABC中,AB=AC.∠A=30°,直线a∥b,顶点 C 在直线b上,直线a交AB 于点D,交AC 于点E,若∠1=145°,则∠2的度数是( )
A.30° B.35° C.40° D.45°
8.如图,在 Rt△ABC 中,D,E 为斜边AB 上的两个点,且BD=BC,AE=AC,则∠DCE 的大小为 .
第8题图 第9题图
9.周长相等的等边三角形 ABC 和等边三角形DEF 按如图所示摆放,重叠部分的周长为6,等边三角形ABC 的边长为 .
10.如图,在△ABC 中,AB=AC,AD⊥BC 于点D.
(1)若∠C=42°,求∠BAD 的度数.
(2)若点 E 在边AB 上,EF∥AC 交AD 的延长线于点F.求证:AE=FE.
11.如图,在△ABC 中,∠A=40°,点D,E 分别在边AB,AC 上,BD=BC=CE,连接CD,BE.
(1)若∠ABC=80°,求∠BDC,∠ABE 的度数.
(2)写出∠BEC 与∠BDC 之间的关系,并说明理由.
C
12.[推理能力]如图,在等边三角形ABC 中,点E 是边AC上一定点,点 D 是直线BC 上一动点,以DE 为边作等边三角形DEF,连接CF.
【问题解决】如图①,若点 D 在边 BC 上,求证:CE+CF=CD.
【类比探究】如图②,若点 D 在边BC 的延长线上,请探究线段CE,CF 与CD 之间存在怎样的数量关系,并说明理由.
考点三:直角三角形的性质与判定
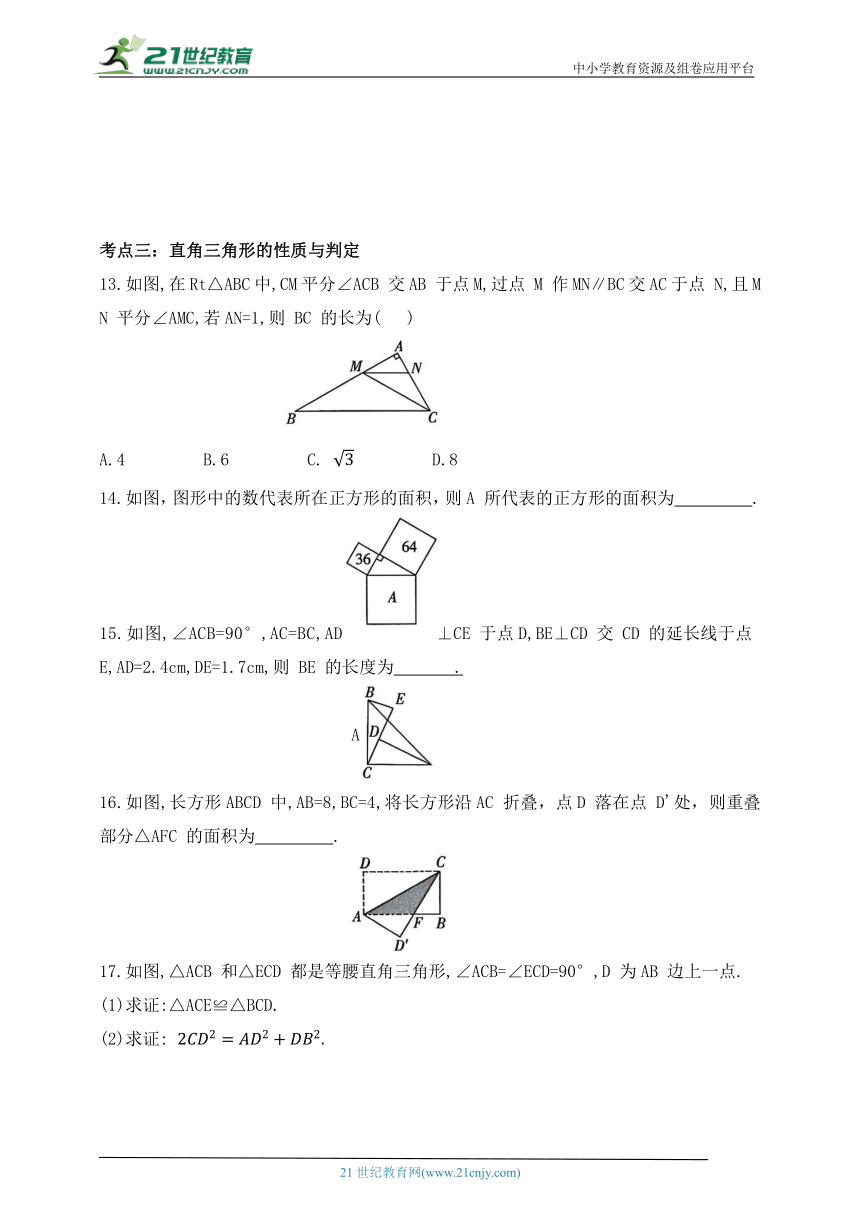
13.如图,在Rt△ABC中,CM平分∠ACB 交AB 于点M,过点 M 作MN∥BC交AC于点 N,且MN 平分∠AMC,若AN=1,则 BC 的长为( )
A.4 B.6 C. D.8
14.如图,图形中的数代表所在正方形的面积,则A 所代表的正方形的面积为 .
15.如图,∠ACB=90°,AC=BC,AD⊥CE 于点D,BE⊥CD 交 CD 的延长线于点 E,AD=2.4cm,DE=1.7cm,则 BE 的长度为 .
A
16.如图,长方形ABCD 中,AB=8,BC=4,将长方形沿AC 折叠,点D 落在点 D'处,则重叠部分△AFC 的面积为 .
17.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB=∠ECD=90°,D 为AB 边上一点.
(1)求证:△ACE≌△BCD.
(2)求证:
B
考点四:线段的垂直平分线的性质与判定
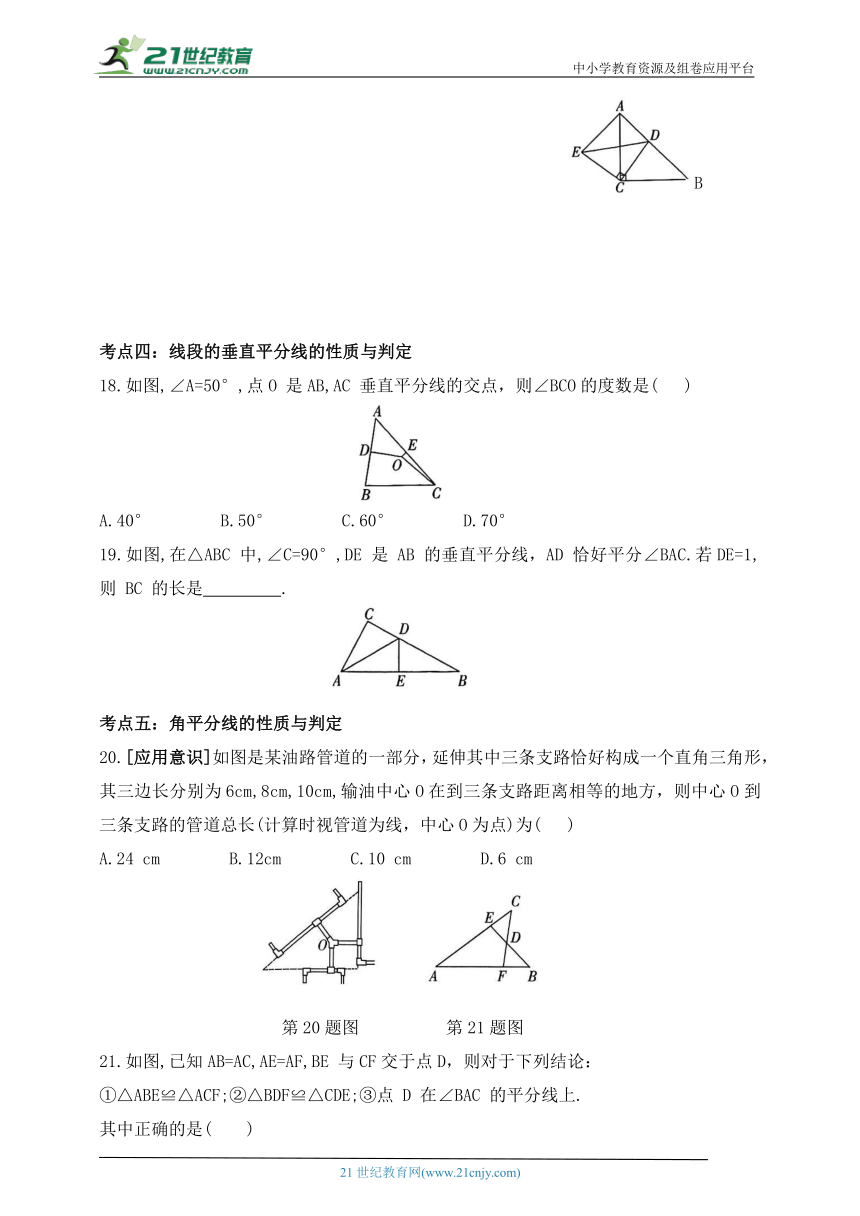
18.如图,∠A=50°,点O 是AB,AC 垂直平分线的交点,则∠BCO的度数是( )
A.40° B.50° C.60° D.70°
19.如图,在△ABC 中,∠C=90°,DE 是 AB 的垂直平分线,AD 恰好平分∠BAC.若DE=1,则 BC 的长是 .
考点五:角平分线的性质与判定
20.[应用意识]如图是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )
A.24 cm B.12cm C.10 cm D.6 cm
第20题图 第21题图
21.如图,已知AB=AC,AE=AF,BE 与CF交于点D,则对于下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点 D 在∠BAC 的平分线上.
其中正确的是( )
A.① B.② C.①和② D.①②③
22.如图,点 P 在∠MON 的平分线上,A,B 分别在∠MON 的边OM,ON 上,若OB=3,S△OPB=6,则线段 AP 的长不可能是( )
A.3 B.4 C.5 D.6
第22题图 第23题图
23.如图,在∠MON 中,以点 O 为圆心,任意长为半径作弧,交射线OM 于点A,交射线ON 于点B,再分别以点A,B 为圆心,OA 的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,连接AB,AC.若OA=5,AB=6,则点 B 到 AC 的距离为( )
A.5 B. C.4 D.
数学思想
思想一:整体思想
1.如图,∠B=∠C,∠1=∠3,则∠1 与∠2之间的关系是( )
C
A.∠1=2∠2 B.3∠1-∠2=180° C.∠1+3∠2=180° D.2∠1+∠2=180°
思想二:分类讨论思想
2.在△ABC 中,AB = AC,∠BAC=100°,点 D 在BC 边上,连接AD,若△ABD 为直角三角形,则∠ADC 的度数为 .
3.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC 中,∠A=80°,则它的特征值k 为 .
思想三:方程思想
4.在△ABC 中,已知 AB = AC,BD 平分∠ABC,交 AC 于点 D,若 BD = BC,求∠DBC 的度数.
参考答案
考点整合
1. B 2. C 3.90°
4.证明:∵∠BAE=∠DAC,∴∠BAE+∠CAE=∠DAC+∠CAE,∴∠CAB=∠EAD.
又∵AB=AD,AC=AE,∴△ABC≌△ADE(SAS),∴∠C=∠E.
5.(1)证明:∵点O 是线段AB 的中点,∴AO=BO.
∵OD∥BC,∴∠AOD = ∠OBC.
在 △AOD 与△OBC 中,∵,∴△AOD≌△OBC(SAS).
(2)解:∵△AOD≌△OBC,∴∠ADO=∠OCB =35°.
∵OD∥BC,∴∠DOC=∠OCB=35°.
6. D 7. C 8. 45° 9. 3
10.(1)解:∵AB=AC,AD⊥BC 于点 D,∴∠BAD=∠CAD,∠ADC = 90°.
又∵∠C= 42°, ∴∠BAD =
(2)证明:∵EF∥AC,∴∠F=∠CAD.
∵∠BAD=∠CAD,∴∠BAD=∠F,∴AE=FE.
11.解:(1)∵∠ABC=80°,BD=BC,∴∠BDC=∠BCD= ×(180°-80°)=50°.
∵∠A+∠ABC+∠ACB=180°,
,∴△BCE 是等边三角形,∴∠EBC=60°,∴∠ABE=∠ABC-∠EBC=20°.
(2)∠BEC+∠BDC=110°.理由:设∠BEC=α,∠BDC=β.
在△ABE 中,α=∠A+∠ABE=40°+∠ABE.
∵CE=BC,∴∠CBE=∠BEC=α,∴∠ABC=∠ABE+∠CBE=α-40°+α=2α-40°.
在△BDC 中,BD=BC,∴∠BDC=∠BCD=β,
∴∠BDC+∠BCD+∠DBC=2β+2α-40°=180°,
∴α+β=110°,∴∠BEC+∠BDC=110°.
12.【问题解决】证明:在CD 上截取CH=CE,连接EH,如图①所示.
∵△ABC 是等边三角形,∴∠ECH =60°,
∴△CEH 是等边三角形,∴EH=EC=CH,∠CEH=60°.
∵△DEF 是等边三角形,∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,∴∠DEH=∠FEC.
在△DEH 和△FEC 中, ∴△DEH≌△FEC(SAS),
∴DH=CF,∴CD=CH+DH=CE+CF,∴CE+CF=CD.
【类比探究】解:CF=CD+CE.理由如下:∵△ABC 是等边三角形,∴∠A=∠B=60°.过点 D 作DG∥AB,交AC的延长线于点G,如图②所示.
∵GD∥AB,∴∠GDC=∠B=60°,∠DGC=∠A=60°,∴∠GDC=∠DGC=60°,
∴△GCD 为等边三角形,∴DG=CD=CG.
∵△EDF 为等边三角形,∴ ED = DF,∠EDF =∠GDC = 60°,∴∠EDG = ∠FDC. 在 △EGD 和 △FCD 中,∵,∴△EGD≌△FCD(SAS),∴EG=FC,
∴FC=EG=CG+CE=CD+CE,即CF=CD+CE.
13. B 14.100 15.0.7cm
16.10 [解析]根据题意易证△AFD'≌△CFB,∴D'F=BF.设. ,则AF=8-x.
在 Rt△AFD'中,由勾股定理得( 解得x=3,
∴AF=AB-FB=
17.证明:(1)∵△ABC 和△ECD 都是等腰直角三角形,∴AC=BC,CE=CD.
∵∠DCE=∠ACB=90°,∴∠ACE+∠ACD=∠BCD+∠ACD,∴∠ACE=∠BCD.
在△ACE 和△BCD 中, △BCD(SAS).
(2)∵△ACB 是等腰直角三角形,∴∠B=∠BAC=45°.
∵△ACE≌△BCD,∴∠B=∠CAE=45°,∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD +AE =DE .
∵△ACE≌△BCD,∴AE=
又∵
18. A 19.3 20. D 21. D 22. A
23. B [解析]连接BC.由题意,得OC 为∠MON 的平分线.
∵OA=OB,OC平分∠AOB,∴OC⊥AB.
设OC 与AB交于点D,作BE⊥AC 于点E.
∵AB=6,OA=5,AC=OA,OC⊥AB,∴AC=5,∠ADC=90°,AD=3,∴CD=4.
在△ABC中,∵ 解得
数学思想
1. B 2.130°或90°
3. 或 [解析]①当∠A 为顶角时,等腰三角形的底角的度数为 ∴特征值 ②当∠A为底角时,顶角的度数为 ∴特征值k 综上所述,特征值k为 或
4.解:设∠C=2x.∵AB=AC,∴∠ABC=∠C=2x.
∵BD=BC,∴∠BDC =∠C = 2x.
∵BD 平分∠ABC,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
章末复习
考点整合
考点一:全等三角形的性质与判定
1.下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
2.如图,点 B,F,C,E 共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF 的是( )
A. AB=DE B.∠A=∠D C. AC=DF D. AC∥FD
第2题图 第3题图
3.如图,在正方形ABCD中,如果AF=BE,那么∠AOD 的度数是 .
4.在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
5.如图,点O 是线段AB 的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC.
(2)若∠ADO=35°,求∠DOC 的度数.
考点二:等腰(边)三角形的性质与判定
6.如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC 的角平分线.若在边 AB 上截取BE=BC,连接DE,则图中等腰三角形共有( )
A.2个 B.3个 C.4个 D.5个
第6题图 第7题图
7.如图,在△ABC中,AB=AC.∠A=30°,直线a∥b,顶点 C 在直线b上,直线a交AB 于点D,交AC 于点E,若∠1=145°,则∠2的度数是( )
A.30° B.35° C.40° D.45°
8.如图,在 Rt△ABC 中,D,E 为斜边AB 上的两个点,且BD=BC,AE=AC,则∠DCE 的大小为 .
第8题图 第9题图
9.周长相等的等边三角形 ABC 和等边三角形DEF 按如图所示摆放,重叠部分的周长为6,等边三角形ABC 的边长为 .
10.如图,在△ABC 中,AB=AC,AD⊥BC 于点D.
(1)若∠C=42°,求∠BAD 的度数.
(2)若点 E 在边AB 上,EF∥AC 交AD 的延长线于点F.求证:AE=FE.
11.如图,在△ABC 中,∠A=40°,点D,E 分别在边AB,AC 上,BD=BC=CE,连接CD,BE.
(1)若∠ABC=80°,求∠BDC,∠ABE 的度数.
(2)写出∠BEC 与∠BDC 之间的关系,并说明理由.
C
12.[推理能力]如图,在等边三角形ABC 中,点E 是边AC上一定点,点 D 是直线BC 上一动点,以DE 为边作等边三角形DEF,连接CF.
【问题解决】如图①,若点 D 在边 BC 上,求证:CE+CF=CD.
【类比探究】如图②,若点 D 在边BC 的延长线上,请探究线段CE,CF 与CD 之间存在怎样的数量关系,并说明理由.
考点三:直角三角形的性质与判定
13.如图,在Rt△ABC中,CM平分∠ACB 交AB 于点M,过点 M 作MN∥BC交AC于点 N,且MN 平分∠AMC,若AN=1,则 BC 的长为( )
A.4 B.6 C. D.8
14.如图,图形中的数代表所在正方形的面积,则A 所代表的正方形的面积为 .
15.如图,∠ACB=90°,AC=BC,AD⊥CE 于点D,BE⊥CD 交 CD 的延长线于点 E,AD=2.4cm,DE=1.7cm,则 BE 的长度为 .
A
16.如图,长方形ABCD 中,AB=8,BC=4,将长方形沿AC 折叠,点D 落在点 D'处,则重叠部分△AFC 的面积为 .
17.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB=∠ECD=90°,D 为AB 边上一点.
(1)求证:△ACE≌△BCD.
(2)求证:
B
考点四:线段的垂直平分线的性质与判定
18.如图,∠A=50°,点O 是AB,AC 垂直平分线的交点,则∠BCO的度数是( )
A.40° B.50° C.60° D.70°
19.如图,在△ABC 中,∠C=90°,DE 是 AB 的垂直平分线,AD 恰好平分∠BAC.若DE=1,则 BC 的长是 .
考点五:角平分线的性质与判定
20.[应用意识]如图是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )
A.24 cm B.12cm C.10 cm D.6 cm
第20题图 第21题图
21.如图,已知AB=AC,AE=AF,BE 与CF交于点D,则对于下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点 D 在∠BAC 的平分线上.
其中正确的是( )
A.① B.② C.①和② D.①②③
22.如图,点 P 在∠MON 的平分线上,A,B 分别在∠MON 的边OM,ON 上,若OB=3,S△OPB=6,则线段 AP 的长不可能是( )
A.3 B.4 C.5 D.6
第22题图 第23题图
23.如图,在∠MON 中,以点 O 为圆心,任意长为半径作弧,交射线OM 于点A,交射线ON 于点B,再分别以点A,B 为圆心,OA 的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,连接AB,AC.若OA=5,AB=6,则点 B 到 AC 的距离为( )
A.5 B. C.4 D.
数学思想
思想一:整体思想
1.如图,∠B=∠C,∠1=∠3,则∠1 与∠2之间的关系是( )
C
A.∠1=2∠2 B.3∠1-∠2=180° C.∠1+3∠2=180° D.2∠1+∠2=180°
思想二:分类讨论思想
2.在△ABC 中,AB = AC,∠BAC=100°,点 D 在BC 边上,连接AD,若△ABD 为直角三角形,则∠ADC 的度数为 .
3.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC 中,∠A=80°,则它的特征值k 为 .
思想三:方程思想
4.在△ABC 中,已知 AB = AC,BD 平分∠ABC,交 AC 于点 D,若 BD = BC,求∠DBC 的度数.
参考答案
考点整合
1. B 2. C 3.90°
4.证明:∵∠BAE=∠DAC,∴∠BAE+∠CAE=∠DAC+∠CAE,∴∠CAB=∠EAD.
又∵AB=AD,AC=AE,∴△ABC≌△ADE(SAS),∴∠C=∠E.
5.(1)证明:∵点O 是线段AB 的中点,∴AO=BO.
∵OD∥BC,∴∠AOD = ∠OBC.
在 △AOD 与△OBC 中,∵,∴△AOD≌△OBC(SAS).
(2)解:∵△AOD≌△OBC,∴∠ADO=∠OCB =35°.
∵OD∥BC,∴∠DOC=∠OCB=35°.
6. D 7. C 8. 45° 9. 3
10.(1)解:∵AB=AC,AD⊥BC 于点 D,∴∠BAD=∠CAD,∠ADC = 90°.
又∵∠C= 42°, ∴∠BAD =
(2)证明:∵EF∥AC,∴∠F=∠CAD.
∵∠BAD=∠CAD,∴∠BAD=∠F,∴AE=FE.
11.解:(1)∵∠ABC=80°,BD=BC,∴∠BDC=∠BCD= ×(180°-80°)=50°.
∵∠A+∠ABC+∠ACB=180°,
,∴△BCE 是等边三角形,∴∠EBC=60°,∴∠ABE=∠ABC-∠EBC=20°.
(2)∠BEC+∠BDC=110°.理由:设∠BEC=α,∠BDC=β.
在△ABE 中,α=∠A+∠ABE=40°+∠ABE.
∵CE=BC,∴∠CBE=∠BEC=α,∴∠ABC=∠ABE+∠CBE=α-40°+α=2α-40°.
在△BDC 中,BD=BC,∴∠BDC=∠BCD=β,
∴∠BDC+∠BCD+∠DBC=2β+2α-40°=180°,
∴α+β=110°,∴∠BEC+∠BDC=110°.
12.【问题解决】证明:在CD 上截取CH=CE,连接EH,如图①所示.
∵△ABC 是等边三角形,∴∠ECH =60°,
∴△CEH 是等边三角形,∴EH=EC=CH,∠CEH=60°.
∵△DEF 是等边三角形,∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,∴∠DEH=∠FEC.
在△DEH 和△FEC 中, ∴△DEH≌△FEC(SAS),
∴DH=CF,∴CD=CH+DH=CE+CF,∴CE+CF=CD.
【类比探究】解:CF=CD+CE.理由如下:∵△ABC 是等边三角形,∴∠A=∠B=60°.过点 D 作DG∥AB,交AC的延长线于点G,如图②所示.
∵GD∥AB,∴∠GDC=∠B=60°,∠DGC=∠A=60°,∴∠GDC=∠DGC=60°,
∴△GCD 为等边三角形,∴DG=CD=CG.
∵△EDF 为等边三角形,∴ ED = DF,∠EDF =∠GDC = 60°,∴∠EDG = ∠FDC. 在 △EGD 和 △FCD 中,∵,∴△EGD≌△FCD(SAS),∴EG=FC,
∴FC=EG=CG+CE=CD+CE,即CF=CD+CE.
13. B 14.100 15.0.7cm
16.10 [解析]根据题意易证△AFD'≌△CFB,∴D'F=BF.设. ,则AF=8-x.
在 Rt△AFD'中,由勾股定理得( 解得x=3,
∴AF=AB-FB=
17.证明:(1)∵△ABC 和△ECD 都是等腰直角三角形,∴AC=BC,CE=CD.
∵∠DCE=∠ACB=90°,∴∠ACE+∠ACD=∠BCD+∠ACD,∴∠ACE=∠BCD.
在△ACE 和△BCD 中, △BCD(SAS).
(2)∵△ACB 是等腰直角三角形,∴∠B=∠BAC=45°.
∵△ACE≌△BCD,∴∠B=∠CAE=45°,∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD +AE =DE .
∵△ACE≌△BCD,∴AE=
又∵
18. A 19.3 20. D 21. D 22. A
23. B [解析]连接BC.由题意,得OC 为∠MON 的平分线.
∵OA=OB,OC平分∠AOB,∴OC⊥AB.
设OC 与AB交于点D,作BE⊥AC 于点E.
∵AB=6,OA=5,AC=OA,OC⊥AB,∴AC=5,∠ADC=90°,AD=3,∴CD=4.
在△ABC中,∵ 解得
数学思想
1. B 2.130°或90°
3. 或 [解析]①当∠A 为顶角时,等腰三角形的底角的度数为 ∴特征值 ②当∠A为底角时,顶角的度数为 ∴特征值k 综上所述,特征值k为 或
4.解:设∠C=2x.∵AB=AC,∴∠ABC=∠C=2x.
∵BD=BC,∴∠BDC =∠C = 2x.
∵BD 平分∠ABC,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
