第十章 三角形的有关证明 专项训练 有关三角形证明的常见题型(二)(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明 专项训练 有关三角形证明的常见题型(二)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 544.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-23 15:28:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
专项训练 三角形的有关证明的常见题型(二)
一、双等腰(边)三角形中的全等模型
1.如图,△ABP 和△CDP 是两个等边三角形,△APD 是以AD 为斜边的等腰直角三角形,连接AC,BC,BD,下列结论:
① △APC≌△BPD;② △ABD≌△BCA;③点 P 在线段 BC 的中垂线上;④∠PBC=15°;⑤AD∥BC;⑥PC⊥AB.
其中正确结论的个数是( )
A.3 B.4 C.5 D.6
2.如图,等边△ABC中,点D,E,F分别在AB,AC,BC 上,且AD=CE=BF,连接 DE,DF,EF,CD 与 BE 交于点 H,下列结论:
①△ADE≌△BFD;②△BDE 与△CFD 的面积相等;③BE=CD;④∠EHC=60°.
其中正确的是( )
A.①②③④ B.①② C.②③④ D.③④
3.新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
(1)如图①,△ABC 和△ADE 互为“兄弟三角形”,点A 为重合的顶角顶点.求证:BD=CE.
(2)如图②,△ABC 和△ADE 互为“兄弟三角形”,点A 为重合的顶角顶点,点D,E均在△ABC 外,连接 BD,CE 交于点 M,连接AM.求证:MA 平分∠BME.
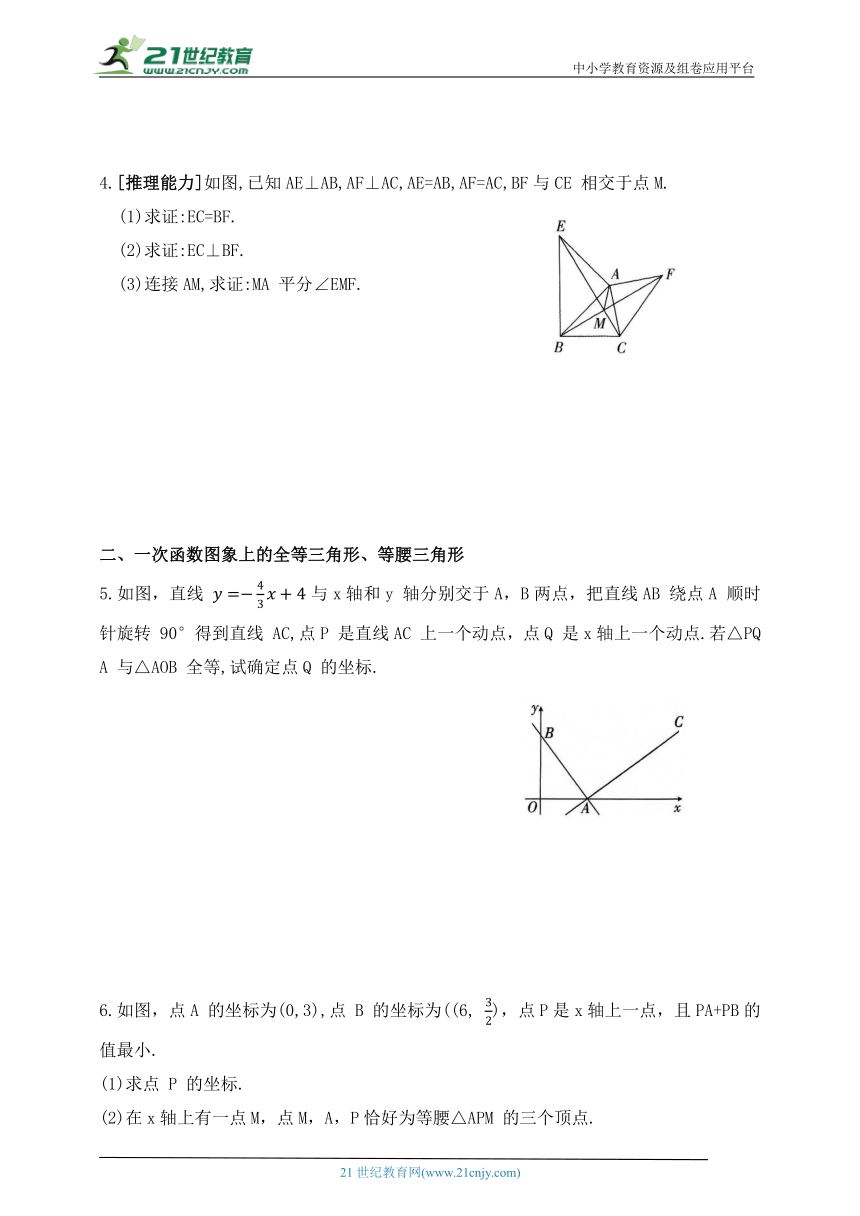
4.[推理能力]如图,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,BF与CE 相交于点M.
(1)求证:EC=BF.
(2)求证:EC⊥BF.
(3)连接AM,求证:MA 平分∠EMF.
二、一次函数图象上的全等三角形、等腰三角形
5.如图,直线 与x轴和y 轴分别交于A,B两点,把直线AB 绕点A 顺时针旋转 90°得到直线 AC,点P 是直线AC 上一个动点,点Q 是x轴上一个动点.若△PQA 与△AOB 全等,试确定点Q 的坐标.
6.如图,点A 的坐标为(0,3),点 B 的坐标为((6, ),点P是x轴上一点,且PA+PB的值最小.
(1)求点 P 的坐标.
(2)在x轴上有一点M,点M,A,P恰好为等腰△APM 的三个顶点.
a.若AP 为△APM 的腰,直接写出点 M 的坐标.
b.若PA 为△APM 的底边,求点 M 的坐标.
7.如图,一次函数 b的图象与坐标轴交于A,B两点,与正比例函数 交于点C(m,4),OA=6.
(1)求一次函数的表达式.
(2)求△BOC 的面积.
(3)在线段AB 上是否存在点 P,使△OAP 是以OA 为底的等腰三角形 若存在,请求出点 P 的坐标;若不存在,请说明理由.
三、三角形中的解题技巧
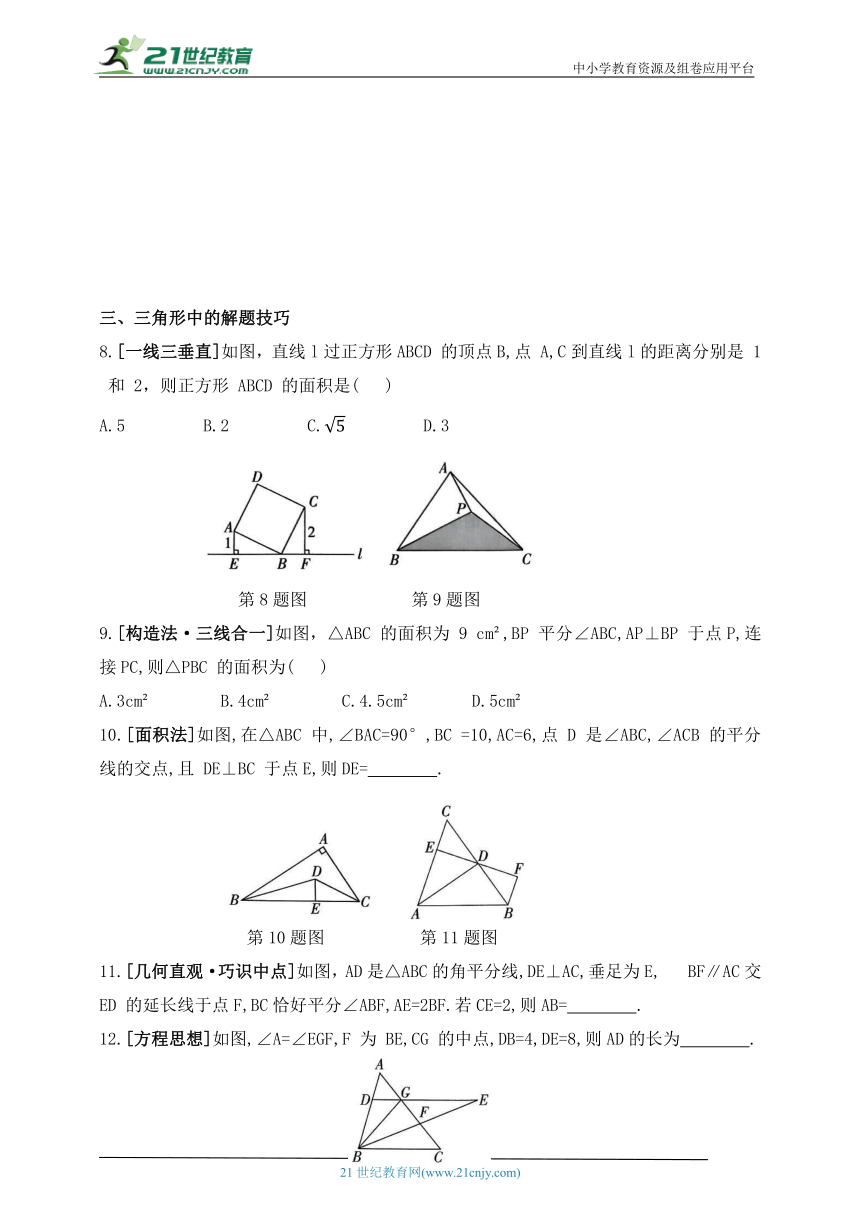
8.[一线三垂直]如图,直线l过正方形ABCD 的顶点B,点 A,C到直线l的距离分别是 1 和 2,则正方形 ABCD 的面积是( )
A.5 B.2 C. D.3
第8题图 第9题图
9.[构造法·三线合一]如图,△ABC 的面积为 9 cm ,BP 平分∠ABC,AP⊥BP 于点P,连接PC,则△PBC 的面积为( )
A.3cm B.4cm C.4.5cm D.5cm
10.[面积法]如图,在△ABC 中,∠BAC=90°,BC =10,AC=6,点 D 是∠ABC,∠ACB 的平分线的交点,且 DE⊥BC 于点E,则DE= .
第10题图 第11题图
11.[几何直观·巧识中点]如图,AD是△ABC的角平分线,DE⊥AC,垂足为E, BF∥AC交ED 的延长线于点F,BC恰好平分∠ABF,AE=2BF.若CE=2,则AB= .
12.[方程思想]如图,∠A=∠EGF,F 为 BE,CG 的中点,DB=4,DE=8,则AD的长为 .
13.[一线三等角]如图,点A,B在射线CA,CB 上,CA=CB.点 E,F 在射线CD上,∠BEC=∠CFA,∠BEC+∠BCA=180°.
(1)求证:△BCE≌△CAF.
(2)试判断线段 EF,BE,AF 的数量关系,并说明理由.
14.[方程思想]如图,在 Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点D以1cm/s的速度从点 A 出发,沿AC 移动到点C,同时点 E 以 3cm/s的速度从点 B 出发,沿BC 移动到点C,两点中有一个点到达终点,两个点都停止运动.直线 PQ 经过Rt△ABC 的点 C,过点 D,E 分别作 DM⊥PQ,EN⊥PQ,垂足分别为点M,N,请问:运动时间t等于多少秒时,CD=CE 说明此时△DCM≌△CEN.
15.[半角模型·截取法]如图 中两边AB,AC上有两点M,N,D为 外一点,且∠A=80°,∠BDC=
(1)猜想线段MN,BM,NC 之间的数量关系并证明.
(2)若. ,求△AMN 的周长.
16.[分类讨论]如图,点E 在等边 的边AB 所在直线上,以EC 为一边作等边 顶点 E,C,F顺时针排序.
(1)点 E 在线段 AB 上,连接 BF.求证:
(2)已知 当 是直角三角形时,求 BE 的长.
参考答案
1. C 2. A
3. 证明:(1)∵△ABC 和△ADE 互为“兄弟三角形”,∴∠BAC=∠DAE,AB=AC,AD=AE,∴∠BAC-∠DAC =∠DAE--∠DAC,即∠BAD =∠CAE.
在△BAD 和△CAE 中, △CAE(SAS),∴BD=CE.
(2)如图,过点 A 作AG⊥BM于点G,AH⊥EM 于点 H.∵△ABC 和△ADE 互为“兄弟三角形”,∴∠BAC=∠DAE,∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD =∠CAE.
在△BAD 和△CAE 中,∵,∴△BAD≌△CAE(SAS),∴∠ABG=∠ACH.
∵AG⊥BM,AH⊥EM,∴∠AGB=∠AHC=90°.又∵AB=AC,∴△ABG≌△ACH(AAS),∴AG=AH.∵AG⊥BM,AH⊥EM,∴MA 平分∠BME.
4.证明:(1)∵AE⊥AB,AF⊥AC,∴∠BAE=∠CAF=90°,∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF.
在△ABF 和△AEC 中, ∴△ABF≌△AEC(SAS),∴EC=BF.
(2)设AB与EC的交点为 D.∵△ABF≌△AEC,∴∠AEC=∠ABF.∵AE⊥AB,∴∠BAE=90°,∴∠AEC+∠ADE=90°.∵∠ADE=∠BDM,∴∠ABF+∠BDM=90°.在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,∴EC⊥BF.
(3)如图,作AP⊥CE 于点 P,AQ⊥BF 于点Q.∵△ABF≌△AEC,∴S△ABF=S△AEC,∴ BF·AQ= EC·AP.∵BF=EC,∴AQ=AP.∵AQ⊥BF,AP⊥CE,∴MA平分∠EMF.
5.解:在 中,令x=0,则y=4,令y=0,则0= 解得x=3,∴OA=3,OB=4,由勾股定理得AB=5.∵∠BAC= 90°,∴∠OAB +∠QAP = 90°。∵∠OAB +∠OBA = 90°,∴∠QAP =∠OBA. ①当∠AQP=90°时,如图甲所示.易得△AOB≌△PQA,∴AQ=OB=4,PQ=OA=3,∴Q (7,0),Q (-1,0).②当∠APQ=90°时,如图乙所示.易得△AOB≌△QPA,∴AQ=AB=5,∴Q (8,0),Q (-2,0).③当∠PAQ=90°时,这种情况不存在.综上所述,点Q 的坐标为(7,0),(8,0),(-1,0),(-2,0).
2.解:(1)如图①,作点C 与点A 关于x轴对称,连接BC 交x轴于点 P,此时PA+PB最小,∴点C的坐标为(0,-3).设直线 BC 的表达式为y=kx+b,则有,解得、直线BC的表达式为令y=0,∴点 P 的坐标为(4,0).
(2)a.在Rt△AOP 中,OA=3,OP=4,∴AP=5,∴AP 为△APM的腰,点 M 的坐标为(9,0)或(-1,0)或(-4,0). b.如图②,作AP 的垂直平分线交AP 于点 N,交x轴于点 M,则MA= MP. 设 OM=x,则 AM = PM = 4-x. 在Rt△AOM中,· ∴点M 的坐标为( , ).
7.解:(1)∵OA=6,∴点A 的坐标为(6,0).将C(m,4)代入y =-2x,∴m=-2,∴点C的坐标为(-2,4).∵一次函数 的图象过A(6,0),C(-2,4), 解得 ∴一次函数的表达式为 y =3,∴点 B 的坐标为(0,3),OB=3,∴△BOC 的面积
(3)存在.如图,作OA 的垂直平分线交x轴于点D,与直线AB的交点即为点 P,连接OP,. 即.xp= ∴点P的坐标为(3, ).
8. A [解析]∵四边形 ABCD 是正方形,∴∠ABC=90°,AB=BC,∴∠ABE+∠CBF=90°.又∵∠AEB=90°,∴ ∠BAE + ∠ABE = 90°, ∴ ∠BAE = ∠CBF. 又∵∠AEB=∠BFC,∴△AEB≌△BFC(AAS),∴BE= ,即正方形 ABCD的面积是5.
9. C [解析]如图,延长 AP 交 BC 于点 E.∵BP 平分∠ABC,∴∠ABP=∠EBP.
∵AP⊥BP,∴∠APB=∠EPB=90°.在△ABP 和△EBP 中,.
∴△ABP≌△EBP(ASA),∴AP =PE,∴S△ABP =
10.2 [解析]∵∠BAC=90°,BC=10,AC=6,∴AB= 过点 D 作DN⊥AB,DM⊥AC,垂足分别为 N,M,连接 DA.∵点 D 是∠ABC,∠ACB 的平分线的交点,且DE⊥BC于点E,∴DE=DN=DM.又∵S△ABC=S△ABD+S△ACD+S△BCD,∴AB·AC=DE×(AB+AC+BC),即8×6=DE×(8+6+10),解得DE=2.
11.6 [解析]∵BF∥AC,∴∠C=∠CBF.
∵BC 平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,∴AB=AC.
∵AD平分∠BAC,∴DC=BD.
在△CDE 与△BDF中,∵∴△CDE ≌△BDF(ASA),
∴DE=DF,CE=BF=2.
∵AE=2BF,∴AC=3BF,∴AB=3BF=6.
12.2 [解析]∵F为BE,CG的中点,∴GF=CF,EF=BF.又∵∠GFE=∠CFB,∴△GFE≌△CFB(SAS),∴GE=BC,∠EGF=∠C.∵∠A =∠EGF,∠AGD=∠EGF 角∴∠A=∠AGD=∠C,∴AD=DG,AB=BC.设AD=DG=x,∵DB=4,DE=8,∴BC=GE=DE-DG=8-3x,AB=4+x,∴4+x=8-x,解得x=2,∴AD=2.
13.(1)证明:∵∠BEC+∠BCA=180°,∴∠BEC+∠ECB+∠ACF = 180°.
∵∠CFA +∠ACF +∠FAC = 180°,∠BEC=∠CFA,∴∠BCE=∠CAF.
在△BCE与△CAF中,,
(2)解:AF+EF=BE.理由如下:
∵△BCE≌△CAF,∴AF=CE,CF=BE.∵CE+EF=CF,∴AF+EF=BE.
14.解:由题意得CD=6-t,CE=8-3t.
∵CD=CE,∴6-t=8-3t,∴t=1.
∵DM⊥PQ,EN⊥PQ,∴∠DMC=∠CNE=90°,∴∠DCM+∠CDM=∠DCM+∠NCE,
∴∠CDM=∠NCE.
又∵CD=CE,∴△DCM≌△CEN(AAS).
15.解:(1)猜想:MN=BM+NC,证明如下:延长AB,在AB的延长线上截取BE=NC,连接DE,如图所示.
在△ABC中,∠A=80°,∴∠ABC+∠ACB=180°-80°=100°.
在△BCD中,∠BDC=100°,∴∠DBC+∠DCB=180°-100°=80°,
∴∠ABC+∠ACB+∠DBC+∠DCB=180°,即∠ABD+∠ACD=180°.
∵∠DBE+∠ABD=180°,∴ ∠DBE = ∠ACD.
在 △DBE 和 △DCN 中,
DN,∠EDB=∠NDC.
∵∠BDC=100°,∠MDN=50°,∴∠BDM+∠NDC=∠BDC-∠MDN=50°,
∴∠MDE=∠BDM+∠EDB=∠BDM+∠NDC=50°,∴∠MDE= ∠MDN = 50°.
在 △MDE 和 △MDN 中,∵,∴△MDE≌△MDN(SAS),∴ME=MN.
∵ME=BM+BE=BM+NC,∴MN=BM+NC.
(2)由(1)可知MN=BM+NC,∴△AMN 的周长为AM+AN+MN=AM+AN+BM+NC=AB+AC.
∵AB=6,AC=7,∴AB+AC=13,∴△AMN 的周长为13.
16.(1)证明:∵△ABC和△ECF为等边三角形,
∴BC=AC,CE=CF,∠BAC=∠ACB=∠ECF=60°,∴∠ACE=∠BCF.
在△ACE 和△BCF 中,∵ ∴△ACE≌△BCF(SAS),∴∠CAE=∠CBF.
∵∠CAE=60°,∴∠FBC=60°,∴∠FBC=∠ACB,∴BF∥AC.
(2)解:①当点 E 在线段AB 上时,∠BFC=90°.
∵BC=AB=6,∠CBF=∠ACB=60°,∴∠BCF=30°.
∵∠ECF=60°,∴∠BCE=30°,∴∠BEC=90°,∴BE= BC=3.
②当点 E 在线段 AB 的延长线上时,∠BCF =90°.
∵∠ECF=60°,∴∠BCE=30°.
∵
综上所述,BE=3或6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
专项训练 三角形的有关证明的常见题型(二)
一、双等腰(边)三角形中的全等模型
1.如图,△ABP 和△CDP 是两个等边三角形,△APD 是以AD 为斜边的等腰直角三角形,连接AC,BC,BD,下列结论:
① △APC≌△BPD;② △ABD≌△BCA;③点 P 在线段 BC 的中垂线上;④∠PBC=15°;⑤AD∥BC;⑥PC⊥AB.
其中正确结论的个数是( )
A.3 B.4 C.5 D.6
2.如图,等边△ABC中,点D,E,F分别在AB,AC,BC 上,且AD=CE=BF,连接 DE,DF,EF,CD 与 BE 交于点 H,下列结论:
①△ADE≌△BFD;②△BDE 与△CFD 的面积相等;③BE=CD;④∠EHC=60°.
其中正确的是( )
A.①②③④ B.①② C.②③④ D.③④
3.新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
(1)如图①,△ABC 和△ADE 互为“兄弟三角形”,点A 为重合的顶角顶点.求证:BD=CE.
(2)如图②,△ABC 和△ADE 互为“兄弟三角形”,点A 为重合的顶角顶点,点D,E均在△ABC 外,连接 BD,CE 交于点 M,连接AM.求证:MA 平分∠BME.
4.[推理能力]如图,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,BF与CE 相交于点M.
(1)求证:EC=BF.
(2)求证:EC⊥BF.
(3)连接AM,求证:MA 平分∠EMF.
二、一次函数图象上的全等三角形、等腰三角形
5.如图,直线 与x轴和y 轴分别交于A,B两点,把直线AB 绕点A 顺时针旋转 90°得到直线 AC,点P 是直线AC 上一个动点,点Q 是x轴上一个动点.若△PQA 与△AOB 全等,试确定点Q 的坐标.
6.如图,点A 的坐标为(0,3),点 B 的坐标为((6, ),点P是x轴上一点,且PA+PB的值最小.
(1)求点 P 的坐标.
(2)在x轴上有一点M,点M,A,P恰好为等腰△APM 的三个顶点.
a.若AP 为△APM 的腰,直接写出点 M 的坐标.
b.若PA 为△APM 的底边,求点 M 的坐标.
7.如图,一次函数 b的图象与坐标轴交于A,B两点,与正比例函数 交于点C(m,4),OA=6.
(1)求一次函数的表达式.
(2)求△BOC 的面积.
(3)在线段AB 上是否存在点 P,使△OAP 是以OA 为底的等腰三角形 若存在,请求出点 P 的坐标;若不存在,请说明理由.
三、三角形中的解题技巧
8.[一线三垂直]如图,直线l过正方形ABCD 的顶点B,点 A,C到直线l的距离分别是 1 和 2,则正方形 ABCD 的面积是( )
A.5 B.2 C. D.3
第8题图 第9题图
9.[构造法·三线合一]如图,△ABC 的面积为 9 cm ,BP 平分∠ABC,AP⊥BP 于点P,连接PC,则△PBC 的面积为( )
A.3cm B.4cm C.4.5cm D.5cm
10.[面积法]如图,在△ABC 中,∠BAC=90°,BC =10,AC=6,点 D 是∠ABC,∠ACB 的平分线的交点,且 DE⊥BC 于点E,则DE= .
第10题图 第11题图
11.[几何直观·巧识中点]如图,AD是△ABC的角平分线,DE⊥AC,垂足为E, BF∥AC交ED 的延长线于点F,BC恰好平分∠ABF,AE=2BF.若CE=2,则AB= .
12.[方程思想]如图,∠A=∠EGF,F 为 BE,CG 的中点,DB=4,DE=8,则AD的长为 .
13.[一线三等角]如图,点A,B在射线CA,CB 上,CA=CB.点 E,F 在射线CD上,∠BEC=∠CFA,∠BEC+∠BCA=180°.
(1)求证:△BCE≌△CAF.
(2)试判断线段 EF,BE,AF 的数量关系,并说明理由.
14.[方程思想]如图,在 Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点D以1cm/s的速度从点 A 出发,沿AC 移动到点C,同时点 E 以 3cm/s的速度从点 B 出发,沿BC 移动到点C,两点中有一个点到达终点,两个点都停止运动.直线 PQ 经过Rt△ABC 的点 C,过点 D,E 分别作 DM⊥PQ,EN⊥PQ,垂足分别为点M,N,请问:运动时间t等于多少秒时,CD=CE 说明此时△DCM≌△CEN.
15.[半角模型·截取法]如图 中两边AB,AC上有两点M,N,D为 外一点,且∠A=80°,∠BDC=
(1)猜想线段MN,BM,NC 之间的数量关系并证明.
(2)若. ,求△AMN 的周长.
16.[分类讨论]如图,点E 在等边 的边AB 所在直线上,以EC 为一边作等边 顶点 E,C,F顺时针排序.
(1)点 E 在线段 AB 上,连接 BF.求证:
(2)已知 当 是直角三角形时,求 BE 的长.
参考答案
1. C 2. A
3. 证明:(1)∵△ABC 和△ADE 互为“兄弟三角形”,∴∠BAC=∠DAE,AB=AC,AD=AE,∴∠BAC-∠DAC =∠DAE--∠DAC,即∠BAD =∠CAE.
在△BAD 和△CAE 中, △CAE(SAS),∴BD=CE.
(2)如图,过点 A 作AG⊥BM于点G,AH⊥EM 于点 H.∵△ABC 和△ADE 互为“兄弟三角形”,∴∠BAC=∠DAE,∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD =∠CAE.
在△BAD 和△CAE 中,∵,∴△BAD≌△CAE(SAS),∴∠ABG=∠ACH.
∵AG⊥BM,AH⊥EM,∴∠AGB=∠AHC=90°.又∵AB=AC,∴△ABG≌△ACH(AAS),∴AG=AH.∵AG⊥BM,AH⊥EM,∴MA 平分∠BME.
4.证明:(1)∵AE⊥AB,AF⊥AC,∴∠BAE=∠CAF=90°,∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF.
在△ABF 和△AEC 中, ∴△ABF≌△AEC(SAS),∴EC=BF.
(2)设AB与EC的交点为 D.∵△ABF≌△AEC,∴∠AEC=∠ABF.∵AE⊥AB,∴∠BAE=90°,∴∠AEC+∠ADE=90°.∵∠ADE=∠BDM,∴∠ABF+∠BDM=90°.在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,∴EC⊥BF.
(3)如图,作AP⊥CE 于点 P,AQ⊥BF 于点Q.∵△ABF≌△AEC,∴S△ABF=S△AEC,∴ BF·AQ= EC·AP.∵BF=EC,∴AQ=AP.∵AQ⊥BF,AP⊥CE,∴MA平分∠EMF.
5.解:在 中,令x=0,则y=4,令y=0,则0= 解得x=3,∴OA=3,OB=4,由勾股定理得AB=5.∵∠BAC= 90°,∴∠OAB +∠QAP = 90°。∵∠OAB +∠OBA = 90°,∴∠QAP =∠OBA. ①当∠AQP=90°时,如图甲所示.易得△AOB≌△PQA,∴AQ=OB=4,PQ=OA=3,∴Q (7,0),Q (-1,0).②当∠APQ=90°时,如图乙所示.易得△AOB≌△QPA,∴AQ=AB=5,∴Q (8,0),Q (-2,0).③当∠PAQ=90°时,这种情况不存在.综上所述,点Q 的坐标为(7,0),(8,0),(-1,0),(-2,0).
2.解:(1)如图①,作点C 与点A 关于x轴对称,连接BC 交x轴于点 P,此时PA+PB最小,∴点C的坐标为(0,-3).设直线 BC 的表达式为y=kx+b,则有,解得、直线BC的表达式为令y=0,∴点 P 的坐标为(4,0).
(2)a.在Rt△AOP 中,OA=3,OP=4,∴AP=5,∴AP 为△APM的腰,点 M 的坐标为(9,0)或(-1,0)或(-4,0). b.如图②,作AP 的垂直平分线交AP 于点 N,交x轴于点 M,则MA= MP. 设 OM=x,则 AM = PM = 4-x. 在Rt△AOM中,· ∴点M 的坐标为( , ).
7.解:(1)∵OA=6,∴点A 的坐标为(6,0).将C(m,4)代入y =-2x,∴m=-2,∴点C的坐标为(-2,4).∵一次函数 的图象过A(6,0),C(-2,4), 解得 ∴一次函数的表达式为 y =3,∴点 B 的坐标为(0,3),OB=3,∴△BOC 的面积
(3)存在.如图,作OA 的垂直平分线交x轴于点D,与直线AB的交点即为点 P,连接OP,. 即.xp= ∴点P的坐标为(3, ).
8. A [解析]∵四边形 ABCD 是正方形,∴∠ABC=90°,AB=BC,∴∠ABE+∠CBF=90°.又∵∠AEB=90°,∴ ∠BAE + ∠ABE = 90°, ∴ ∠BAE = ∠CBF. 又∵∠AEB=∠BFC,∴△AEB≌△BFC(AAS),∴BE= ,即正方形 ABCD的面积是5.
9. C [解析]如图,延长 AP 交 BC 于点 E.∵BP 平分∠ABC,∴∠ABP=∠EBP.
∵AP⊥BP,∴∠APB=∠EPB=90°.在△ABP 和△EBP 中,.
∴△ABP≌△EBP(ASA),∴AP =PE,∴S△ABP =
10.2 [解析]∵∠BAC=90°,BC=10,AC=6,∴AB= 过点 D 作DN⊥AB,DM⊥AC,垂足分别为 N,M,连接 DA.∵点 D 是∠ABC,∠ACB 的平分线的交点,且DE⊥BC于点E,∴DE=DN=DM.又∵S△ABC=S△ABD+S△ACD+S△BCD,∴AB·AC=DE×(AB+AC+BC),即8×6=DE×(8+6+10),解得DE=2.
11.6 [解析]∵BF∥AC,∴∠C=∠CBF.
∵BC 平分∠ABF,∴∠ABC=∠CBF,∴∠C=∠ABC,∴AB=AC.
∵AD平分∠BAC,∴DC=BD.
在△CDE 与△BDF中,∵∴△CDE ≌△BDF(ASA),
∴DE=DF,CE=BF=2.
∵AE=2BF,∴AC=3BF,∴AB=3BF=6.
12.2 [解析]∵F为BE,CG的中点,∴GF=CF,EF=BF.又∵∠GFE=∠CFB,∴△GFE≌△CFB(SAS),∴GE=BC,∠EGF=∠C.∵∠A =∠EGF,∠AGD=∠EGF 角∴∠A=∠AGD=∠C,∴AD=DG,AB=BC.设AD=DG=x,∵DB=4,DE=8,∴BC=GE=DE-DG=8-3x,AB=4+x,∴4+x=8-x,解得x=2,∴AD=2.
13.(1)证明:∵∠BEC+∠BCA=180°,∴∠BEC+∠ECB+∠ACF = 180°.
∵∠CFA +∠ACF +∠FAC = 180°,∠BEC=∠CFA,∴∠BCE=∠CAF.
在△BCE与△CAF中,,
(2)解:AF+EF=BE.理由如下:
∵△BCE≌△CAF,∴AF=CE,CF=BE.∵CE+EF=CF,∴AF+EF=BE.
14.解:由题意得CD=6-t,CE=8-3t.
∵CD=CE,∴6-t=8-3t,∴t=1.
∵DM⊥PQ,EN⊥PQ,∴∠DMC=∠CNE=90°,∴∠DCM+∠CDM=∠DCM+∠NCE,
∴∠CDM=∠NCE.
又∵CD=CE,∴△DCM≌△CEN(AAS).
15.解:(1)猜想:MN=BM+NC,证明如下:延长AB,在AB的延长线上截取BE=NC,连接DE,如图所示.
在△ABC中,∠A=80°,∴∠ABC+∠ACB=180°-80°=100°.
在△BCD中,∠BDC=100°,∴∠DBC+∠DCB=180°-100°=80°,
∴∠ABC+∠ACB+∠DBC+∠DCB=180°,即∠ABD+∠ACD=180°.
∵∠DBE+∠ABD=180°,∴ ∠DBE = ∠ACD.
在 △DBE 和 △DCN 中,
DN,∠EDB=∠NDC.
∵∠BDC=100°,∠MDN=50°,∴∠BDM+∠NDC=∠BDC-∠MDN=50°,
∴∠MDE=∠BDM+∠EDB=∠BDM+∠NDC=50°,∴∠MDE= ∠MDN = 50°.
在 △MDE 和 △MDN 中,∵,∴△MDE≌△MDN(SAS),∴ME=MN.
∵ME=BM+BE=BM+NC,∴MN=BM+NC.
(2)由(1)可知MN=BM+NC,∴△AMN 的周长为AM+AN+MN=AM+AN+BM+NC=AB+AC.
∵AB=6,AC=7,∴AB+AC=13,∴△AMN 的周长为13.
16.(1)证明:∵△ABC和△ECF为等边三角形,
∴BC=AC,CE=CF,∠BAC=∠ACB=∠ECF=60°,∴∠ACE=∠BCF.
在△ACE 和△BCF 中,∵ ∴△ACE≌△BCF(SAS),∴∠CAE=∠CBF.
∵∠CAE=60°,∴∠FBC=60°,∴∠FBC=∠ACB,∴BF∥AC.
(2)解:①当点 E 在线段AB 上时,∠BFC=90°.
∵BC=AB=6,∠CBF=∠ACB=60°,∴∠BCF=30°.
∵∠ECF=60°,∴∠BCE=30°,∴∠BEC=90°,∴BE= BC=3.
②当点 E 在线段 AB 的延长线上时,∠BCF =90°.
∵∠ECF=60°,∴∠BCE=30°.
∵
综上所述,BE=3或6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
