第十章 三角形的有关证明 专项训练 有关三角形证明的常见题型(一)(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明 专项训练 有关三角形证明的常见题型(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 468.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
专项训练 有关三角形证明的常见题型(一)
一、角平分线与线段垂直平分线的综合应用
1.如图,△AOB 的外角∠CAB,∠DBA 的平分线AP,BP 相交于点P,PE⊥OC 于点 E,PF⊥OD 于点 F.下列结论:①PE=PF;②点 P 在∠COD 的平分线上; ,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.如图,在△ABC 中,AD 是∠BAC的平分线,AD 的垂直平分线交AB于点 E,交CB 的延长线于 点 F,连接DE,AF.
(1)判断DE 与AC 的位置关系,并说明你所得的结论.
(2)求证:∠C=∠EAF.
3.如图,已知△ABC 中,AD 是∠BAC 的平分线,DE⊥AB 于点 E,DF⊥AC 于点 F,连接EF 交AD 于点G.
(1)求证:AD 垂直平分EF.
(2)若AB+AC=10,DE=3,求△ABC 的面积.
二、等腰三角形与全等三角形的综合应用
4.如图,点A 是x轴上一个定点,点B从原点O 出发沿y 轴的正方向移动,以线段OB 为边在 y 轴右侧作等边三角形,以线段AB 为边在AB 上方作等边三角形,连接CD,随点 B 的移动,下列说法错误的是( )
A.△BOA≌△BDC
B.∠ODC=150°
C.直线CD 与x轴所夹的锐角恒为60°
D.随点 B 的移动,线段CD 的值逐渐增大
5.如图,已知 △ABC≌△ADE,∠ABC =∠ADE=90°,BC与DE 交于点F.
(1)求∠ACB+∠DAE 的度数.
(2)连接AF,在不添加辅助线的情况下,请直接写出图中所有全等三角形.(不包括已知全等三角形)
6.在△ABC中,AB=AC,点 E,D分别是AB,AC 上一点,连接CE,BD,且BD=BC.
(1)如图①,当CE⊥AB,∠CBD=50°时,求∠BCE 的度数.
(2)如图②,取 CE 的中点F,连接 BF,若∠CBD=∠ABF.求证:AC=2BF.
三、轴对称——最短路线问题
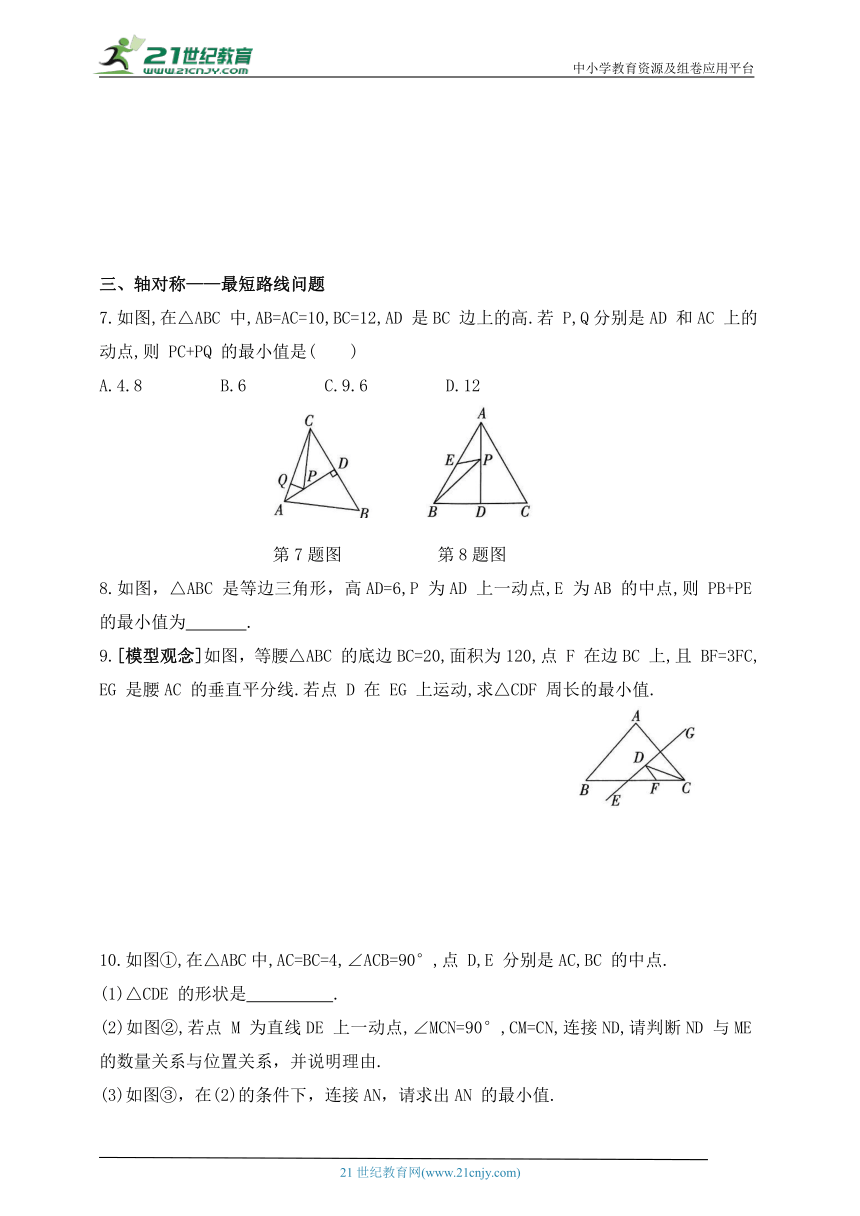
7.如图,在△ABC 中,AB=AC=10,BC=12,AD 是BC 边上的高.若 P,Q分别是AD 和AC 上的动点,则 PC+PQ 的最小值是( )
A.4.8 B.6 C.9.6 D.12
第7题图 第8题图
8.如图,△ABC 是等边三角形,高AD=6,P 为AD 上一动点,E 为AB 的中点,则 PB+PE 的最小值为 .
9.[模型观念]如图,等腰△ABC 的底边BC=20,面积为120,点 F 在边BC 上,且 BF=3FC,EG 是腰AC 的垂直平分线.若点 D 在 EG 上运动,求△CDF 周长的最小值.
10.如图①,在△ABC中,AC=BC=4,∠ACB=90°,点 D,E 分别是AC,BC 的中点.
(1)△CDE 的形状是 .
(2)如图②,若点 M 为直线DE 上一动点,∠MCN=90°,CM=CN,连接ND,请判断ND 与ME 的数量关系与位置关系,并说明理由.
(3)如图③,在(2)的条件下,连接AN,请求出AN 的最小值.
参考答案
1. C [解析]①如图,作 PH⊥AB 于点 H.
∵AP 是∠CAB的平分线,∴∠PAE=∠PAH.
在△PEA 和△PHA 中,,∴△PEA≌△PHA(AAS).∴PE=PH.
∵BP平分∠ABD,且PH⊥BA,PF⊥BD,∴PF=PH,∴PE=PF,∴①正确.②由①可知PE=PF.∵PE⊥OC 于点 E,PF⊥OD 于点 F,∴点 P 在∠COD的平分线上,∴②正确.③∵∠O+∠OEP+∠EPF+∠OFP=360°,∠OEP+∠OFP=90°+90°=180°,∴∠O+ ∠EPF=180°,即∠O+∠EPA+∠HPA+∠HPB+∠FPB = 180°. 由①知△PEA≌△PHA,∴∠EPA=∠HPA,同理可得∠FPB=∠HPB,∴∠O+2(∠HPA+∠HPB)=180°,即∠O+2∠APB=180°, ③错误.
2.(1)解:DE∥AC,理由:∵AD 是∠BAC 的平分线,∴∠CAD=∠BAD.
∵EF 垂直平分AD,∴AE=DE,∴∠BAD=∠EDA,∴∠CAD=∠EDA,∴DE∥AC.
(2)证明:∵EF垂直平分AD,∴EA=ED,FA=FD.
在△AEF 和△DEF 中, (SSS),∴∠EAF=∠EDF.
∵DE∥AC,∴∠C=∠EDF,∴∠C=∠EAF.
3.(1)证明:∵DE⊥AB,DF⊥AC,∴∠DEA=∠DFA=90°.
∵AD 是∠BAC 的平分线,∴∠EAD=∠FAD.
在△AED 和△AFD 中,∵,∴△AED≌△AFD(AAS),∴AE=AF.
∵AD 是∠BAC 的平分线,∴AG⊥EF,EG=FG,∴AD 垂直平分EF.
(2)解:∵AD是∠BAC的平分线,DE⊥AB 于点 E,DF⊥AC 于点 F,∴DE=DF.
∵DE=3,∴DF=3.
∵AB+AC=10,∴△ABC的面积 AC)·DE=15.
4. D [解析]∵△OBD 和△ABC 都是等边三角形,∴∠ABC=∠OBD=∠ODB=∠BOD=60°,BO=BD,BC=AB,∴∠OBD-∠DBA=∠ABC-∠DBA,∴∠ABO=∠CBD,∴△BOA≌△BDC(SAS).故 A 不符合题意.∵△BOA≌△BDC,∴∠BDC=∠BOA=90°,∴∠ODC 故 B不符合题意.如图,延长CD 交x轴于点E.∵∠ODC=150°,∴∠ODE=180°-∠ODC=30°.∵∠BOA =90°,∠BOD =60°,∴∠DOA=∠BOA-∠BOD=30°,∴∠DEA=∠DOA+∠ODE=60°,∴直线CD 与x轴所夹的锐角恒为60°.故C不符合题意.∵△BOA≌△BDC,∴CD=OA.∵点A 是x轴上一个定点,∴OA 的值是一个定值,∴随点 B的移动,线段CD 的值不变.故D符合题意.
5.解:(1)∵△ABC≌△ADE,∴∠CAB=∠EAD.
在△ACB中,∠ABC=90°,∴∠ACB+∠CAB=90°,∴∠ACB+∠DAE=90°.
(2)△ADC≌△ABE,△ACF≌△AEF,△CDF≌△EBF,△ADF≌△ABF.
6.(1)解:设∠ABD=α.
∵∠CBD=50°,∴∠ABC=∠CBD+∠ABD=50°+α.
∵AB=AC,∴∠ACB=∠ABC=50°+α.
又∵BD=BC,∴∠BDC=∠ACB=50°+α.
在△BCD中,∠CBD+∠BDC+∠ACB=180°,∴50°+50°+α+50°+α=180°,
∴α=15°,∴∠ABC=50°+α=65°.
∵CE⊥AB,∴∠BCE+∠ABC=90°,∴∠BCE=90°-
(2)证明:延长BF到点G,使FG=BF,连接CG,如图.
∵F 为CE 的中点,∴CF=EF.
在△CFG 和△EFB 中,∵∴△CFG≌△EFB(SAS),∴∠G=∠ABF,
∴AB∥CG,∴∠ABC+∠BCG=180°.
∵AB=AC,∴∠ACB=∠ABC.
∵BD=BC,∴∠BDC=∠ACB,∴∠ABC = ∠BDC,∴ ∠BDC +∠BCG = 180°.
又∵∠BDC+∠BDA=180°,∴∠BCG=∠BDA.
∵∠CBD=∠ABF,∴∠CBG+∠DBF=∠ABD+∠DBF,即∠CBG = ∠ABD.
在△BCG和△BDA 中,∵,∴△BCG≌△BDA(ASA),∴BG=AB.
∵BG=BF+FG=2BF,AB=AC,∴AC=2BF.
7. C [解析]如图,连接BP.∵AB=AC,AD 是BC边上的高,∴AD 垂直平分BC,. ∴当点B,P,Q在同一条直线上,且BQ⊥AC时,PC+PQ的值最小.∴ - =9.6,∴PC+PQ的最小值是9.6.
8.6 [解析]∵△ABC为等边三角形,AD 为高,∴B,C 两点关于直线AD 对称.如图,连接CE,则CE与AD的交点即为使PB+PE 是最小值的点P',即PB+PE 的最小值为 ∵E为AB 的中点,∴CE⊥AB,即CE 为△ABC的高线,∴CE=AD=6,∴PB+PE 的最小值为6.
9.解:如图,作AH⊥BC 于点H,连接AD.∵EG 垂直平分线段AC,∴DA=DC,∴DF+DC=AD+DF,∴当A,D,F共线时,DF+DC的值最小,最小值就是线段AF 的长.∵ BC·AH=120,∴AH=12.∵AB=AC,AH⊥BC,∴BH=CH=10.∵BF=3FC,∴CF=FH=5,∴AF= C的最小值为13,∴△CDF 周长的最小值为13+5=18.
10.解:(1)等腰直角三角形
(2)ND=ME,ND⊥ME.
理由:∵∠DCE=∠MCN,∴∠NCD=∠MCE.∵CD=CE,CN=CM, ∴△DCN≌△ECM(SAS),∴ND =ME,∠CEM=∠CDN,∴∠NDM=∠CDE+∠DEC=90°,∴ND⊥ME. (3)如图,连接BM,作 BH⊥DE 于点 H.与(2)同理得,△ACN≌△BCM(SAS),∴AN = BM,∴AN 的最小值为BH. ∴AN 的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
专项训练 有关三角形证明的常见题型(一)
一、角平分线与线段垂直平分线的综合应用
1.如图,△AOB 的外角∠CAB,∠DBA 的平分线AP,BP 相交于点P,PE⊥OC 于点 E,PF⊥OD 于点 F.下列结论:①PE=PF;②点 P 在∠COD 的平分线上; ,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.如图,在△ABC 中,AD 是∠BAC的平分线,AD 的垂直平分线交AB于点 E,交CB 的延长线于 点 F,连接DE,AF.
(1)判断DE 与AC 的位置关系,并说明你所得的结论.
(2)求证:∠C=∠EAF.
3.如图,已知△ABC 中,AD 是∠BAC 的平分线,DE⊥AB 于点 E,DF⊥AC 于点 F,连接EF 交AD 于点G.
(1)求证:AD 垂直平分EF.
(2)若AB+AC=10,DE=3,求△ABC 的面积.
二、等腰三角形与全等三角形的综合应用
4.如图,点A 是x轴上一个定点,点B从原点O 出发沿y 轴的正方向移动,以线段OB 为边在 y 轴右侧作等边三角形,以线段AB 为边在AB 上方作等边三角形,连接CD,随点 B 的移动,下列说法错误的是( )
A.△BOA≌△BDC
B.∠ODC=150°
C.直线CD 与x轴所夹的锐角恒为60°
D.随点 B 的移动,线段CD 的值逐渐增大
5.如图,已知 △ABC≌△ADE,∠ABC =∠ADE=90°,BC与DE 交于点F.
(1)求∠ACB+∠DAE 的度数.
(2)连接AF,在不添加辅助线的情况下,请直接写出图中所有全等三角形.(不包括已知全等三角形)
6.在△ABC中,AB=AC,点 E,D分别是AB,AC 上一点,连接CE,BD,且BD=BC.
(1)如图①,当CE⊥AB,∠CBD=50°时,求∠BCE 的度数.
(2)如图②,取 CE 的中点F,连接 BF,若∠CBD=∠ABF.求证:AC=2BF.
三、轴对称——最短路线问题
7.如图,在△ABC 中,AB=AC=10,BC=12,AD 是BC 边上的高.若 P,Q分别是AD 和AC 上的动点,则 PC+PQ 的最小值是( )
A.4.8 B.6 C.9.6 D.12
第7题图 第8题图
8.如图,△ABC 是等边三角形,高AD=6,P 为AD 上一动点,E 为AB 的中点,则 PB+PE 的最小值为 .
9.[模型观念]如图,等腰△ABC 的底边BC=20,面积为120,点 F 在边BC 上,且 BF=3FC,EG 是腰AC 的垂直平分线.若点 D 在 EG 上运动,求△CDF 周长的最小值.
10.如图①,在△ABC中,AC=BC=4,∠ACB=90°,点 D,E 分别是AC,BC 的中点.
(1)△CDE 的形状是 .
(2)如图②,若点 M 为直线DE 上一动点,∠MCN=90°,CM=CN,连接ND,请判断ND 与ME 的数量关系与位置关系,并说明理由.
(3)如图③,在(2)的条件下,连接AN,请求出AN 的最小值.
参考答案
1. C [解析]①如图,作 PH⊥AB 于点 H.
∵AP 是∠CAB的平分线,∴∠PAE=∠PAH.
在△PEA 和△PHA 中,,∴△PEA≌△PHA(AAS).∴PE=PH.
∵BP平分∠ABD,且PH⊥BA,PF⊥BD,∴PF=PH,∴PE=PF,∴①正确.②由①可知PE=PF.∵PE⊥OC 于点 E,PF⊥OD 于点 F,∴点 P 在∠COD的平分线上,∴②正确.③∵∠O+∠OEP+∠EPF+∠OFP=360°,∠OEP+∠OFP=90°+90°=180°,∴∠O+ ∠EPF=180°,即∠O+∠EPA+∠HPA+∠HPB+∠FPB = 180°. 由①知△PEA≌△PHA,∴∠EPA=∠HPA,同理可得∠FPB=∠HPB,∴∠O+2(∠HPA+∠HPB)=180°,即∠O+2∠APB=180°, ③错误.
2.(1)解:DE∥AC,理由:∵AD 是∠BAC 的平分线,∴∠CAD=∠BAD.
∵EF 垂直平分AD,∴AE=DE,∴∠BAD=∠EDA,∴∠CAD=∠EDA,∴DE∥AC.
(2)证明:∵EF垂直平分AD,∴EA=ED,FA=FD.
在△AEF 和△DEF 中, (SSS),∴∠EAF=∠EDF.
∵DE∥AC,∴∠C=∠EDF,∴∠C=∠EAF.
3.(1)证明:∵DE⊥AB,DF⊥AC,∴∠DEA=∠DFA=90°.
∵AD 是∠BAC 的平分线,∴∠EAD=∠FAD.
在△AED 和△AFD 中,∵,∴△AED≌△AFD(AAS),∴AE=AF.
∵AD 是∠BAC 的平分线,∴AG⊥EF,EG=FG,∴AD 垂直平分EF.
(2)解:∵AD是∠BAC的平分线,DE⊥AB 于点 E,DF⊥AC 于点 F,∴DE=DF.
∵DE=3,∴DF=3.
∵AB+AC=10,∴△ABC的面积 AC)·DE=15.
4. D [解析]∵△OBD 和△ABC 都是等边三角形,∴∠ABC=∠OBD=∠ODB=∠BOD=60°,BO=BD,BC=AB,∴∠OBD-∠DBA=∠ABC-∠DBA,∴∠ABO=∠CBD,∴△BOA≌△BDC(SAS).故 A 不符合题意.∵△BOA≌△BDC,∴∠BDC=∠BOA=90°,∴∠ODC 故 B不符合题意.如图,延长CD 交x轴于点E.∵∠ODC=150°,∴∠ODE=180°-∠ODC=30°.∵∠BOA =90°,∠BOD =60°,∴∠DOA=∠BOA-∠BOD=30°,∴∠DEA=∠DOA+∠ODE=60°,∴直线CD 与x轴所夹的锐角恒为60°.故C不符合题意.∵△BOA≌△BDC,∴CD=OA.∵点A 是x轴上一个定点,∴OA 的值是一个定值,∴随点 B的移动,线段CD 的值不变.故D符合题意.
5.解:(1)∵△ABC≌△ADE,∴∠CAB=∠EAD.
在△ACB中,∠ABC=90°,∴∠ACB+∠CAB=90°,∴∠ACB+∠DAE=90°.
(2)△ADC≌△ABE,△ACF≌△AEF,△CDF≌△EBF,△ADF≌△ABF.
6.(1)解:设∠ABD=α.
∵∠CBD=50°,∴∠ABC=∠CBD+∠ABD=50°+α.
∵AB=AC,∴∠ACB=∠ABC=50°+α.
又∵BD=BC,∴∠BDC=∠ACB=50°+α.
在△BCD中,∠CBD+∠BDC+∠ACB=180°,∴50°+50°+α+50°+α=180°,
∴α=15°,∴∠ABC=50°+α=65°.
∵CE⊥AB,∴∠BCE+∠ABC=90°,∴∠BCE=90°-
(2)证明:延长BF到点G,使FG=BF,连接CG,如图.
∵F 为CE 的中点,∴CF=EF.
在△CFG 和△EFB 中,∵∴△CFG≌△EFB(SAS),∴∠G=∠ABF,
∴AB∥CG,∴∠ABC+∠BCG=180°.
∵AB=AC,∴∠ACB=∠ABC.
∵BD=BC,∴∠BDC=∠ACB,∴∠ABC = ∠BDC,∴ ∠BDC +∠BCG = 180°.
又∵∠BDC+∠BDA=180°,∴∠BCG=∠BDA.
∵∠CBD=∠ABF,∴∠CBG+∠DBF=∠ABD+∠DBF,即∠CBG = ∠ABD.
在△BCG和△BDA 中,∵,∴△BCG≌△BDA(ASA),∴BG=AB.
∵BG=BF+FG=2BF,AB=AC,∴AC=2BF.
7. C [解析]如图,连接BP.∵AB=AC,AD 是BC边上的高,∴AD 垂直平分BC,. ∴当点B,P,Q在同一条直线上,且BQ⊥AC时,PC+PQ的值最小.∴ - =9.6,∴PC+PQ的最小值是9.6.
8.6 [解析]∵△ABC为等边三角形,AD 为高,∴B,C 两点关于直线AD 对称.如图,连接CE,则CE与AD的交点即为使PB+PE 是最小值的点P',即PB+PE 的最小值为 ∵E为AB 的中点,∴CE⊥AB,即CE 为△ABC的高线,∴CE=AD=6,∴PB+PE 的最小值为6.
9.解:如图,作AH⊥BC 于点H,连接AD.∵EG 垂直平分线段AC,∴DA=DC,∴DF+DC=AD+DF,∴当A,D,F共线时,DF+DC的值最小,最小值就是线段AF 的长.∵ BC·AH=120,∴AH=12.∵AB=AC,AH⊥BC,∴BH=CH=10.∵BF=3FC,∴CF=FH=5,∴AF= C的最小值为13,∴△CDF 周长的最小值为13+5=18.
10.解:(1)等腰直角三角形
(2)ND=ME,ND⊥ME.
理由:∵∠DCE=∠MCN,∴∠NCD=∠MCE.∵CD=CE,CN=CM, ∴△DCN≌△ECM(SAS),∴ND =ME,∠CEM=∠CDN,∴∠NDM=∠CDE+∠DEC=90°,∴ND⊥ME. (3)如图,连接BM,作 BH⊥DE 于点 H.与(2)同理得,△ACN≌△BCM(SAS),∴AN = BM,∴AN 的最小值为BH. ∴AN 的最小值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
