第十章 三角形的有关证明 检测题(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明 检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 452.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-23 19:08:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
五四制鲁教版数学七年级下册
第十章检测题
时间:90分钟 满分:150分
一、选择题(每题4分,共40分)
1.下列定理中逆定理不正确的是( )
A.角平分线上的点到这个角的两边的距离相等
B.在一个三角形中,如果两边相等,那么它们所对的角也相等
C.同位角相等,两直线平行
D.全等三角形的对应角相等
2.如图,点D,E 分别在线段AB,AC上,CD与BE 相交于O点,已知 AB=AC,现添加以下的哪个条件可以判定△ABE≌△ACD ( )
A.∠B=∠C B. AD=BD C. BO=CO D. BE=CD
第2题图 第3题图
3.两个同样大小的直角三角板按如图所示摆放,其中两条一样长的直角边交于点 M,另一直角边 BE,CD 分别落在 的边AP 和AQ 上,且. 连接AM,则在说明AM为 的平分线的过程中,理由正确的是( )
A. SAS B. SSA C. HL D. SSS
4.如图,已知OC平分 若 则CD等于( )
A.3cm B.4cm C.1.5cm D.2cm
第4题图 第5题图
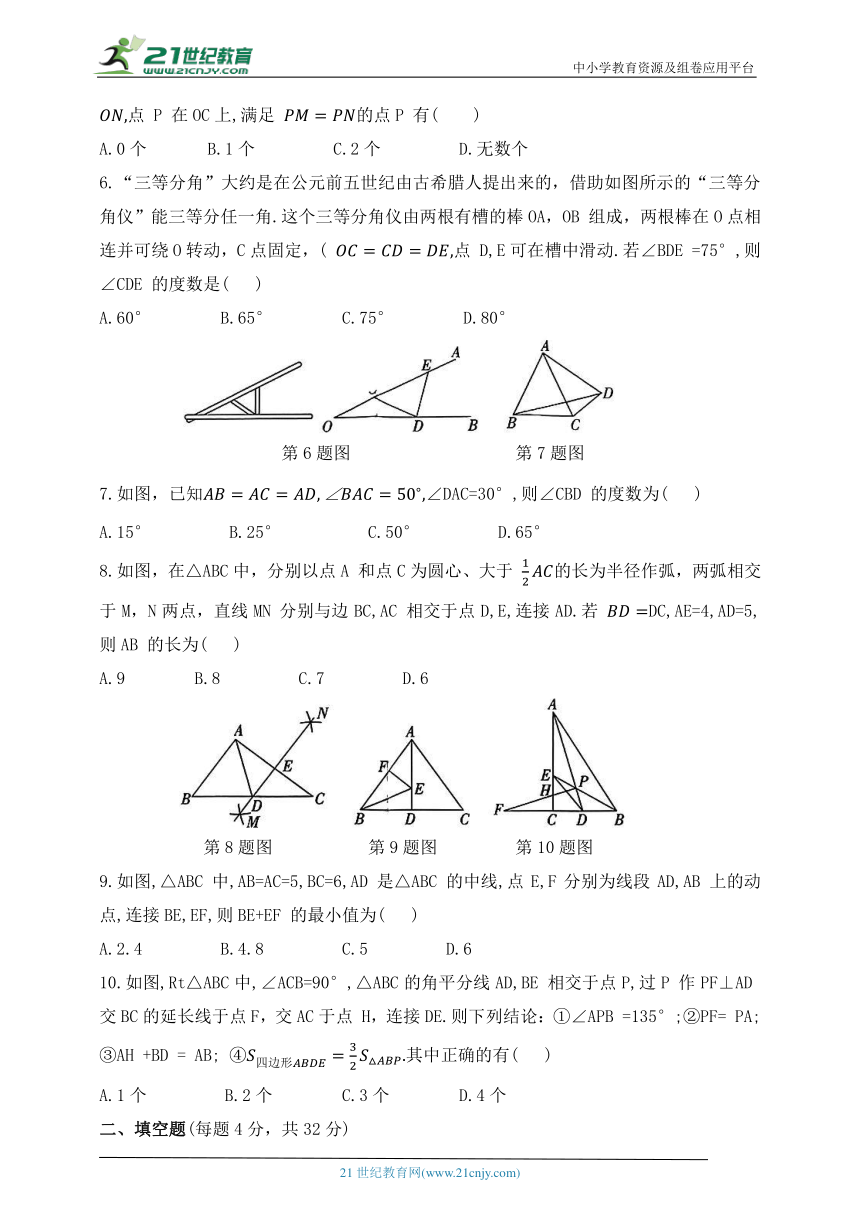
5.如图,射线OC 为 的平分线,点M,N 分别是边OA,OB 上的两个定点,且 点 P 在OC上,满足 的点P 有( )
A.0个 B.1个 C.2个 D.无数个
6.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB 组成,两根棒在O点相连并可绕O转动,C点固定,( 点 D,E可在槽中滑动.若∠BDE =75°,则∠CDE 的度数是( )
A.60° B.65° C.75° D.80°
第6题图 第7题图
7.如图,已知∠DAC=30°,则∠CBD 的度数为( )
A.15° B.25° C.50° D.65°
8.如图,在△ABC中,分别以点A 和点C为圆心、大于 的长为半径作弧,两弧相交于M,N两点,直线MN 分别与边BC,AC 相交于点D,E,连接AD.若 DC,AE=4,AD=5,则AB 的长为( )
A.9 B.8 C.7 D.6
第8题图 第9题图 第10题图
9.如图,△ABC 中,AB=AC=5,BC=6,AD 是△ABC 的中线,点E,F分别为线段AD,AB 上的动点,连接BE,EF,则BE+EF 的最小值为( )
A.2.4 B.4.8 C.5 D.6
10.如图,Rt△ABC中,∠ACB=90°,△ABC的角平分线AD,BE 相交于点P,过P 作PF⊥AD 交BC的延长线于点F,交AC于点 H,连接DE.则下列结论:①∠APB =135°;②PF= PA;③AH +BD = AB; 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题4分,共32分)
11.小曹同学复习时将几种三角形的关系整理如图所示,请帮他在括号内填上一个适当的条件: .
12.如图,△ABC 中,AB=AC,点 D,E 都在边BC上,∠BAD=∠CAE.若BD=9,则CE 的长为 .
第12题图 第13题图 第14题图
13.如图,在△ABC 中,∠C=90°,∠ABC=60°,BD 平分∠ABC.若AD=6,则
14.如图所示的“弦图”是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.若直角三角形的斜边长为13,一条直角边长为12,则小正方形ABCD的面积为 .
15.如图所示,AD 是△ABC 的中线,∠ADC=45°.把△ADC沿直线AD 折叠,点C 落在点C'的位置上,连接BC',如果BC=4,那么.
16.我们规定:等腰三角形的顶角与一个底角度数的比值称为等腰三角形的“特征值”,记作k.若 则该等腰三角形的顶角为 度.
17.如图,在四边形ABEF 中,AB=4,EF=6,点C是BE上一点,连接AC,CF,若AC=CF,∠B=∠E=∠ACF,则BE 的长为 .
18.如图,在△ABC中,点D 是AB上一点,CD平分∠ACB,∠A=2∠ADC,BD=6,AC=4,则BC 的长为 .
三、解答题(共78分)
19.(10分)如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:BD=CE.
20.(12分)如图,△ABC 中,AB=AC,点E,F在边BC上,BE=CF,点D 在AF 的延长线上,AD=AC.
(1)求证:△ABE≌△ACF.
(2)若∠BAE=30°,则∠ADC= °.
21.(12分)如图,AD 为△ABC 的角平分线,DE⊥AB 于点E,DF⊥AC 于点F,连接EF 交AD 于点O.
(1)求证:AD 垂直平分EF.
(2)若∠BAC=60°,写出DO与AD 之间的数量关系,并证明.
22.(14分)如图,在. 中, 所对的边分别为a,b,c.
(1)若 请直接写出 与 的和与 的大小关系.
(2)求证: 的内角和等干
(3)若求证: 是直角三角形.
23.(14分)如图,等边 的边长为4cm,点M 从点B 出发沿BC运动,同时,点 N 从点A出发沿线段CA 的延长线运动,点M,N的速度均为 点M 到达点C时,两点停止运动.作 于点D,连接MN 交AB 于点E.设点M,N 的运动时间为 ts.
(1)当 为等腰三角形时,求t的值.
(2)线段DE 的长度是否为定值 若是,请求出其长度;若不是,请说明理由.
24.(16分)【问题背景】(1)如图①,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点 D,E,易证DE,BD,CE 三条线段的数量关系为DE= .
【拓展延伸】(2)如图②,将(1)中的条件改为在△ABC 中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请求出DE,BD,CE 三条线段的数量关系,并证明.
【实际应用】(3)如图③,在△ACB 中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点 A 的坐标为(-6,3),请写出点 B 的坐标.
参考答案
1. D 2. A 3. C 4. A 5. B
6. D [解析]∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC,∴∠DCE=∠O+∠ODC=2∠ODC.∵∠O+∠OED= 3∠ODC =∠BDE = 75°, ∴∠ODC = 25°. 105°-∠ODC=80°.
7. A 8. D 9. B
10. C [解析]∵在△ABC 中,∠ACB=90°,∴∠BAC+∠ABC=90°.又∵AD,BE 分别平分∠BAC,∠ABC, 135°,故①正确.又∵PF⊥AD,∠BPD=180°-∠APB 又∵∠ABP=∠FBP,BP=BP,∴△ABP≌△FBP(ASA),∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.在△APH 和△FPD 中,∵∠APH=∠FPD=90°,∠PAH=∠BAP=∠DFP,PA=PF,∴△APH≌△FPD(ASA),∴AH=FD.又∵AB=FB,∴AB=FD+BD=AH+BD,故③正确.连接 HD,如图.∵△ABP≌△FBP,△APH≌△FPD,∴S△APB=S△FPB,S△APH=S△FPD,PH=PD.∵∠HPD=90°,∴∠HDP=∠DHP=45°= ∠BPD, ∴ HD ∥EP,∴ S△EPH = S△EPD. 故④不正确.∴正确的有①②③,共3个.
11.∠B=60°(答案不唯一) 12.9 13.3 14.49 15. 16.36
17.10 18.10
19.证明:∵AB⊥AC,AD⊥AE,∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,∴∠CAE=∠BAD.又∵AB=AC,∠ABD=∠ACE,∴△ABD≌△ACE(ASA),∴BD=CE.
20.(1)证明:∵AB=AC,∴∠B=∠ACF.
在△ABE 和△ACF中,,
(2)75
21.(1)证明:∵AD 为△ABC的角平分线,DE⊥AB 于点E,DF⊥AC于点F,
∴DE=DF,∠AED=90°,∠AFD=90°,∴∠DEF=∠DFE,∴∠AEF=∠AFE.
在△AOE和△AOF 中,∵(AAS),
∴OE =OF,∠AOE =∠AOF.
∵∠AOE +∠AOF=180°,∴∠AOE=∠AOF=90°,∴AO⊥EF,∴AD 垂直平分 EF.
(2)解: AD = 4OD. 证明:∵∠BAC=60°,AD 为△ABC 的角平分线,∴∠EAO=30°.又∵∠AED=90°,∴△AED 是直角三角形,∴AD=2DE.∵∠AED=90°,∴∠ADE=60°.∵∠EOD=90°,∴∠DEO=30°,∴在直角三角形 DOE 中DE=2OD,∴AD=4OD.
22.(1)解:∠A+∠B<∠C.
(2)证明:如图,过点 B 作MN∥AC. ∵MN∥AC,∴∠MBA =∠A,∠NBC=∠C.∵∠MBA+∠ABC+∠NBC=180°,∴∠A+∠ABC+∠C=180°, 即△ABC的内角和等于180°.
(3)证明:是直角三角形.
23.解:(1)由题意,得AN=BM=t.∵等边△ABC 的边长为4,∴∠C=∠BAC=60°,CM=4-t,CN=4+t.当△AEN 为等腰三角形时,AN=AE=t.∵∠EAN=180°-60°=120°,∴∠ENA=30°.∴∠CMN=180°-30°-60°=90°.∴CN=2CM,即4+t=2(4-t),解得
(2)线段DE 的长度为定值.理由如下:如图,过点 M 作MF∥AC交AB 于点F,∴∠ANE=∠FME,∠BFM=∠BAC=60°.∵∠B=60°,∴△BFM 为等边三角形,∴FM=BM=AN.∵MD⊥AB,∴BD=DF= BF.
在△EFM 和△EAN 中,
即线段DE 的长度为2cm.
24.解:(1)BD+CE (2)DE=BD+CE.
证明:在△ABD中,∠ABD=180°-∠ADB-∠BAD.
又∵∠CAE=180°-∠BAC-∠BAD,∠BDA=∠BAC,∴∠ABD=∠CAE.
在△ABD和△CAE中,∵∴△ABD≌△CAE(AAS),
∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.
(3)作AE⊥x轴于点E,BF⊥x轴于点 F.
∵点C 的坐标为(-2,0),点 A 的坐标为(-6,3),∴AE=3,OE=6,OC=2.
由(1)知,△AEC≌△CFB,∴CF=AE=3,BF=CE=OE-OC=4,
∴OF=CF-OC=1,∴点B 的坐标为(1,4).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
五四制鲁教版数学七年级下册
第十章检测题
时间:90分钟 满分:150分
一、选择题(每题4分,共40分)
1.下列定理中逆定理不正确的是( )
A.角平分线上的点到这个角的两边的距离相等
B.在一个三角形中,如果两边相等,那么它们所对的角也相等
C.同位角相等,两直线平行
D.全等三角形的对应角相等
2.如图,点D,E 分别在线段AB,AC上,CD与BE 相交于O点,已知 AB=AC,现添加以下的哪个条件可以判定△ABE≌△ACD ( )
A.∠B=∠C B. AD=BD C. BO=CO D. BE=CD
第2题图 第3题图
3.两个同样大小的直角三角板按如图所示摆放,其中两条一样长的直角边交于点 M,另一直角边 BE,CD 分别落在 的边AP 和AQ 上,且. 连接AM,则在说明AM为 的平分线的过程中,理由正确的是( )
A. SAS B. SSA C. HL D. SSS
4.如图,已知OC平分 若 则CD等于( )
A.3cm B.4cm C.1.5cm D.2cm
第4题图 第5题图
5.如图,射线OC 为 的平分线,点M,N 分别是边OA,OB 上的两个定点,且 点 P 在OC上,满足 的点P 有( )
A.0个 B.1个 C.2个 D.无数个
6.“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB 组成,两根棒在O点相连并可绕O转动,C点固定,( 点 D,E可在槽中滑动.若∠BDE =75°,则∠CDE 的度数是( )
A.60° B.65° C.75° D.80°
第6题图 第7题图
7.如图,已知∠DAC=30°,则∠CBD 的度数为( )
A.15° B.25° C.50° D.65°
8.如图,在△ABC中,分别以点A 和点C为圆心、大于 的长为半径作弧,两弧相交于M,N两点,直线MN 分别与边BC,AC 相交于点D,E,连接AD.若 DC,AE=4,AD=5,则AB 的长为( )
A.9 B.8 C.7 D.6
第8题图 第9题图 第10题图
9.如图,△ABC 中,AB=AC=5,BC=6,AD 是△ABC 的中线,点E,F分别为线段AD,AB 上的动点,连接BE,EF,则BE+EF 的最小值为( )
A.2.4 B.4.8 C.5 D.6
10.如图,Rt△ABC中,∠ACB=90°,△ABC的角平分线AD,BE 相交于点P,过P 作PF⊥AD 交BC的延长线于点F,交AC于点 H,连接DE.则下列结论:①∠APB =135°;②PF= PA;③AH +BD = AB; 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题4分,共32分)
11.小曹同学复习时将几种三角形的关系整理如图所示,请帮他在括号内填上一个适当的条件: .
12.如图,△ABC 中,AB=AC,点 D,E 都在边BC上,∠BAD=∠CAE.若BD=9,则CE 的长为 .
第12题图 第13题图 第14题图
13.如图,在△ABC 中,∠C=90°,∠ABC=60°,BD 平分∠ABC.若AD=6,则
14.如图所示的“弦图”是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.若直角三角形的斜边长为13,一条直角边长为12,则小正方形ABCD的面积为 .
15.如图所示,AD 是△ABC 的中线,∠ADC=45°.把△ADC沿直线AD 折叠,点C 落在点C'的位置上,连接BC',如果BC=4,那么.
16.我们规定:等腰三角形的顶角与一个底角度数的比值称为等腰三角形的“特征值”,记作k.若 则该等腰三角形的顶角为 度.
17.如图,在四边形ABEF 中,AB=4,EF=6,点C是BE上一点,连接AC,CF,若AC=CF,∠B=∠E=∠ACF,则BE 的长为 .
18.如图,在△ABC中,点D 是AB上一点,CD平分∠ACB,∠A=2∠ADC,BD=6,AC=4,则BC 的长为 .
三、解答题(共78分)
19.(10分)如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:BD=CE.
20.(12分)如图,△ABC 中,AB=AC,点E,F在边BC上,BE=CF,点D 在AF 的延长线上,AD=AC.
(1)求证:△ABE≌△ACF.
(2)若∠BAE=30°,则∠ADC= °.
21.(12分)如图,AD 为△ABC 的角平分线,DE⊥AB 于点E,DF⊥AC 于点F,连接EF 交AD 于点O.
(1)求证:AD 垂直平分EF.
(2)若∠BAC=60°,写出DO与AD 之间的数量关系,并证明.
22.(14分)如图,在. 中, 所对的边分别为a,b,c.
(1)若 请直接写出 与 的和与 的大小关系.
(2)求证: 的内角和等干
(3)若求证: 是直角三角形.
23.(14分)如图,等边 的边长为4cm,点M 从点B 出发沿BC运动,同时,点 N 从点A出发沿线段CA 的延长线运动,点M,N的速度均为 点M 到达点C时,两点停止运动.作 于点D,连接MN 交AB 于点E.设点M,N 的运动时间为 ts.
(1)当 为等腰三角形时,求t的值.
(2)线段DE 的长度是否为定值 若是,请求出其长度;若不是,请说明理由.
24.(16分)【问题背景】(1)如图①,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点 D,E,易证DE,BD,CE 三条线段的数量关系为DE= .
【拓展延伸】(2)如图②,将(1)中的条件改为在△ABC 中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请求出DE,BD,CE 三条线段的数量关系,并证明.
【实际应用】(3)如图③,在△ACB 中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点 A 的坐标为(-6,3),请写出点 B 的坐标.
参考答案
1. D 2. A 3. C 4. A 5. B
6. D [解析]∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC,∴∠DCE=∠O+∠ODC=2∠ODC.∵∠O+∠OED= 3∠ODC =∠BDE = 75°, ∴∠ODC = 25°. 105°-∠ODC=80°.
7. A 8. D 9. B
10. C [解析]∵在△ABC 中,∠ACB=90°,∴∠BAC+∠ABC=90°.又∵AD,BE 分别平分∠BAC,∠ABC, 135°,故①正确.又∵PF⊥AD,∠BPD=180°-∠APB 又∵∠ABP=∠FBP,BP=BP,∴△ABP≌△FBP(ASA),∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.在△APH 和△FPD 中,∵∠APH=∠FPD=90°,∠PAH=∠BAP=∠DFP,PA=PF,∴△APH≌△FPD(ASA),∴AH=FD.又∵AB=FB,∴AB=FD+BD=AH+BD,故③正确.连接 HD,如图.∵△ABP≌△FBP,△APH≌△FPD,∴S△APB=S△FPB,S△APH=S△FPD,PH=PD.∵∠HPD=90°,∴∠HDP=∠DHP=45°= ∠BPD, ∴ HD ∥EP,∴ S△EPH = S△EPD. 故④不正确.∴正确的有①②③,共3个.
11.∠B=60°(答案不唯一) 12.9 13.3 14.49 15. 16.36
17.10 18.10
19.证明:∵AB⊥AC,AD⊥AE,∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,∴∠CAE=∠BAD.又∵AB=AC,∠ABD=∠ACE,∴△ABD≌△ACE(ASA),∴BD=CE.
20.(1)证明:∵AB=AC,∴∠B=∠ACF.
在△ABE 和△ACF中,,
(2)75
21.(1)证明:∵AD 为△ABC的角平分线,DE⊥AB 于点E,DF⊥AC于点F,
∴DE=DF,∠AED=90°,∠AFD=90°,∴∠DEF=∠DFE,∴∠AEF=∠AFE.
在△AOE和△AOF 中,∵(AAS),
∴OE =OF,∠AOE =∠AOF.
∵∠AOE +∠AOF=180°,∴∠AOE=∠AOF=90°,∴AO⊥EF,∴AD 垂直平分 EF.
(2)解: AD = 4OD. 证明:∵∠BAC=60°,AD 为△ABC 的角平分线,∴∠EAO=30°.又∵∠AED=90°,∴△AED 是直角三角形,∴AD=2DE.∵∠AED=90°,∴∠ADE=60°.∵∠EOD=90°,∴∠DEO=30°,∴在直角三角形 DOE 中DE=2OD,∴AD=4OD.
22.(1)解:∠A+∠B<∠C.
(2)证明:如图,过点 B 作MN∥AC. ∵MN∥AC,∴∠MBA =∠A,∠NBC=∠C.∵∠MBA+∠ABC+∠NBC=180°,∴∠A+∠ABC+∠C=180°, 即△ABC的内角和等于180°.
(3)证明:是直角三角形.
23.解:(1)由题意,得AN=BM=t.∵等边△ABC 的边长为4,∴∠C=∠BAC=60°,CM=4-t,CN=4+t.当△AEN 为等腰三角形时,AN=AE=t.∵∠EAN=180°-60°=120°,∴∠ENA=30°.∴∠CMN=180°-30°-60°=90°.∴CN=2CM,即4+t=2(4-t),解得
(2)线段DE 的长度为定值.理由如下:如图,过点 M 作MF∥AC交AB 于点F,∴∠ANE=∠FME,∠BFM=∠BAC=60°.∵∠B=60°,∴△BFM 为等边三角形,∴FM=BM=AN.∵MD⊥AB,∴BD=DF= BF.
在△EFM 和△EAN 中,
即线段DE 的长度为2cm.
24.解:(1)BD+CE (2)DE=BD+CE.
证明:在△ABD中,∠ABD=180°-∠ADB-∠BAD.
又∵∠CAE=180°-∠BAC-∠BAD,∠BDA=∠BAC,∴∠ABD=∠CAE.
在△ABD和△CAE中,∵∴△ABD≌△CAE(AAS),
∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.
(3)作AE⊥x轴于点E,BF⊥x轴于点 F.
∵点C 的坐标为(-2,0),点 A 的坐标为(-6,3),∴AE=3,OE=6,OC=2.
由(1)知,△AEC≌△CFB,∴CF=AE=3,BF=CE=OE-OC=4,
∴OF=CF-OC=1,∴点B 的坐标为(1,4).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
