青岛版七年级下13.3.1圆的初步认识课件(共23张PPT)
文档属性
| 名称 | 青岛版七年级下13.3.1圆的初步认识课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 288.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-18 10:36:19 | ||
图片预览






文档简介
课件23张PPT。第一课时
圆的基本概念泰山出版社数学学科七年级
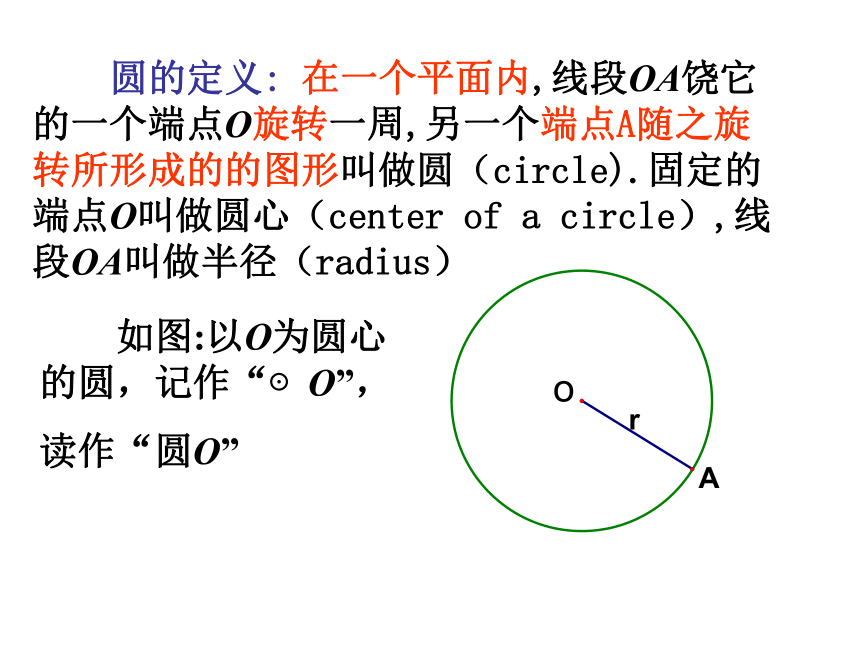
下学期多媒体教学课件 §13.3 圆的初步认识正三角形、正方形、正六边形1.用同一种正多边形能密铺地面的有哪几种? 2.用同一种多边形能密铺地面的只有有哪几种? 三角形、四边形、正六边形两种正多边形的能密铺的有哪几种?3461284三种正多边形的能密铺的有哪几种?346124612圆是生活中常见的图形,许多物体都给我们以圆的形象让大风车转起来大风车.gsp 圆的定义: 在一个平面内,线段OA饶它的一个端点O旋转一周,另一个端点A随之旋转所形成的的图形叫做圆(circle).固定的端点O叫做圆心(center of a circle),线段OA叫做半径(radius) 如图:以O为圆心的圆,记作“⊙O”,
读作“圆O”由圆的定义可知:
(1) 圆上的各点到定点(圆心O)的距离等于定长(半径的长r );
(2)到定点的距离等于定长的点都在圆上因此,圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.请你用集合的语言描述下面的两个概念:
(1)圆的内部是 点的集合.
(2)圆的外部是 点的集合.知识点二:点与圆的位置关系实验与探究: 画一个半径是5厘米的⊙O ,在⊙O上任取A、B两点,连接OA与OB,
(1)你知道OA与OB的长分别是多少吗?
(2)如果OC=5厘米,你能说出点C的位置吗?
(3)如果OM=7厘米,ON=3厘米,你能说出M、N两点与圆的位置关系吗?
(4)想一想平面上的点与圆有几种位置关系?OAB5厘米让你来总结:
点与圆的三种位置关系:
(1)点在圆上(2)点在圆内
(3)点在圆外OAB5厘米让你来总结:
点与圆的三种位置关系:
(1)点在圆上
(2)点在圆内
(3)点在圆外跟踪练习1:作业精编第73页的
第1——5题.点A是圆上的点OA是圆的半径 连接圆上任意两点的线段叫做弦 经过圆心的弦叫做直径如图中的BD如图中的线段BC、BD圆上任意两点间的部分叫做圆弧,简称弧.直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心的弦叫做直径(如直径AC).⌒COBA小于半圆的弧叫做劣弧.如AB大于半圆的弧叫做优弧(用三个点表示)如BCA弧的分类: (1)优弧(大于半圆的弧)
(2)半圆弧(等于半圆的弧)
(3)劣弧(小于半圆的弧)︵︵跟踪练习2:作业精编第73页的
第6——9题.实验与探究 分别观察图(1)与图(2),你发现图(1)中的两枚硬币所确定的两个圆有什么特点(也可以自己取两枚相同硬币来观察)?图(2)中的几个圆有什么共同点和不同点?能够重合的圆叫做等圆圆心相同、半径不等的圆叫做同心圆问题5 知识运用:有两个同心圆,大圆半径
为 ,小圆半径为 ,求圆环的面积。 因为圆环的面积是大圆面积与小圆面积的差,
所以,圆环的面积为
跟踪练习3:作业精编第73页的
第10——11题. 1.连接圆上任意两点的线段叫做弦第一组:区别弦和弧的定义:2.圆上任意两点间的部分叫做圆弧,简称弧.第二组:区别等圆和同心圆的定义:①能够重合的圆叫做等圆圆心相同、半径不等的圆叫做同心圆等圆:②半径相等的圆叫做等圆③直径相等的圆叫做等圆同心圆:圆心相同、半径相等的圆叫做同圆第三组:等弧定义:在同圆或等圆中,能够互相重合的弧叫做等弧 。例1:弧长相等的弧叫等弧。例2:长度相等的两条弧叫等弧。××一点P到圆上各点的最大距离为8cm,最小距离为2cm,则圆的半径是___________分析:分两种情况讨论这节课你学会了什么?知识点二:点与圆的位置关系知识点三:圆中的弦和弧知识点四:等圆和同心圆知识点一:圆的有关概念
圆的基本概念泰山出版社数学学科七年级
下学期多媒体教学课件 §13.3 圆的初步认识正三角形、正方形、正六边形1.用同一种正多边形能密铺地面的有哪几种? 2.用同一种多边形能密铺地面的只有有哪几种? 三角形、四边形、正六边形两种正多边形的能密铺的有哪几种?3461284三种正多边形的能密铺的有哪几种?346124612圆是生活中常见的图形,许多物体都给我们以圆的形象让大风车转起来大风车.gsp 圆的定义: 在一个平面内,线段OA饶它的一个端点O旋转一周,另一个端点A随之旋转所形成的的图形叫做圆(circle).固定的端点O叫做圆心(center of a circle),线段OA叫做半径(radius) 如图:以O为圆心的圆,记作“⊙O”,
读作“圆O”由圆的定义可知:
(1) 圆上的各点到定点(圆心O)的距离等于定长(半径的长r );
(2)到定点的距离等于定长的点都在圆上因此,圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.请你用集合的语言描述下面的两个概念:
(1)圆的内部是 点的集合.
(2)圆的外部是 点的集合.知识点二:点与圆的位置关系实验与探究: 画一个半径是5厘米的⊙O ,在⊙O上任取A、B两点,连接OA与OB,
(1)你知道OA与OB的长分别是多少吗?
(2)如果OC=5厘米,你能说出点C的位置吗?
(3)如果OM=7厘米,ON=3厘米,你能说出M、N两点与圆的位置关系吗?
(4)想一想平面上的点与圆有几种位置关系?OAB5厘米让你来总结:
点与圆的三种位置关系:
(1)点在圆上(2)点在圆内
(3)点在圆外OAB5厘米让你来总结:
点与圆的三种位置关系:
(1)点在圆上
(2)点在圆内
(3)点在圆外跟踪练习1:作业精编第73页的
第1——5题.点A是圆上的点OA是圆的半径 连接圆上任意两点的线段叫做弦 经过圆心的弦叫做直径如图中的BD如图中的线段BC、BD圆上任意两点间的部分叫做圆弧,简称弧.直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心的弦叫做直径(如直径AC).⌒COBA小于半圆的弧叫做劣弧.如AB大于半圆的弧叫做优弧(用三个点表示)如BCA弧的分类: (1)优弧(大于半圆的弧)
(2)半圆弧(等于半圆的弧)
(3)劣弧(小于半圆的弧)︵︵跟踪练习2:作业精编第73页的
第6——9题.实验与探究 分别观察图(1)与图(2),你发现图(1)中的两枚硬币所确定的两个圆有什么特点(也可以自己取两枚相同硬币来观察)?图(2)中的几个圆有什么共同点和不同点?能够重合的圆叫做等圆圆心相同、半径不等的圆叫做同心圆问题5 知识运用:有两个同心圆,大圆半径
为 ,小圆半径为 ,求圆环的面积。 因为圆环的面积是大圆面积与小圆面积的差,
所以,圆环的面积为
跟踪练习3:作业精编第73页的
第10——11题. 1.连接圆上任意两点的线段叫做弦第一组:区别弦和弧的定义:2.圆上任意两点间的部分叫做圆弧,简称弧.第二组:区别等圆和同心圆的定义:①能够重合的圆叫做等圆圆心相同、半径不等的圆叫做同心圆等圆:②半径相等的圆叫做等圆③直径相等的圆叫做等圆同心圆:圆心相同、半径相等的圆叫做同圆第三组:等弧定义:在同圆或等圆中,能够互相重合的弧叫做等弧 。例1:弧长相等的弧叫等弧。例2:长度相等的两条弧叫等弧。××一点P到圆上各点的最大距离为8cm,最小距离为2cm,则圆的半径是___________分析:分两种情况讨论这节课你学会了什么?知识点二:点与圆的位置关系知识点三:圆中的弦和弧知识点四:等圆和同心圆知识点一:圆的有关概念
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
