第三章图形的平移与旋转单元试卷(含答案)北师大版数学八下
文档属性
| 名称 | 第三章图形的平移与旋转单元试卷(含答案)北师大版数学八下 |  | |
| 格式 | docx | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 15:44:54 | ||
图片预览

文档简介
第三章图形的平移与旋转 单元试卷北师大版数学八下
学校:___________姓名:___________班级:___________
一、单选题
1.下列哪个图形是由图平移得到的是( )
A. B.
C. D.
2.将长度为3㎝的线段向下平移2㎝,则平移后的线段长度是( )
A.3㎝ B.2㎝ C.5㎝ D.1㎝
3.在平面直角坐标系中,将点向下平移2个单位长度得到点Q,若点Q在x轴上,则点P的坐标为( )
A. B. C. D.
4.如图(1)中,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图(1)作为“基本图形”绕着A点经过逆时针旋转得到图(2).两次旋转的角度分别为( )
A.45°,90° B.90°,45° C.60°,30° D.30°,60°
5.如图,在直角坐标系中,线段是将绕着点逆时针旋转一定角度后得到的的一部分,则点的对应点的坐标是( )
A.(-2,3) B.(-3,2) C.(-2,4) D.(-3,3)
6.如图是一块长方形的场地,长,宽,从、两处入口的中路宽都为,两小路汇合处路宽为,其余部分种植草坪,则草坪面积为( )
A.m2 B.m2 C.m2 D.m2
7.如图,在△ABC中,∠BAC=45°,AC=8,动点E从点A出发沿射线AB运动,连接CE,将CE绕点C顺时针旋转45°得到CF,连接AF,则△AFC的面积变化情况是( ).
A.先变大再变小 B.先变小再变大 C.逐渐变大 D.不变
8.如图,在等边中,,点在上,且,是上一动点,连接,将线段绕点逆时针旋转得到线段,若使点恰好落在上,则线段的长是( )
A.4 B.5 C.6 D.8
9.如图,点是等边三角形内一点,,,,则与的面积之和为( )
A. B. C. D.
10.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2026,则n的值为( )
A.407 B.406 C.405 D.404
二、填空题
11.如图是一个旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的度数至少为 °.
12.将点先向右平移2个单位,再向上平移3个单位后,则平移后点的坐标是 .
13.如图,边长为2的等边的边在x轴上,将绕原点O逆时针旋转得到三角形,则点的坐标为 .
14.如图,将绕着点逆时针旋转后得到,若,,则的度数为 .
15.如图,小正方形方格的边长都是1,点A、B、C、D、O都是小正方形的顶点.若COD是由AOB绕点O按顺时针方向旋转一次得到的,则至少需要旋转 °.
16.如图,是绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是 .
17.如图,在ABC中,AB=AC=6,∠B=30°,边BC上一个动点M从B运动到C,连AM,将射线AM绕M顺顺时针转30°交AC于N,则N的路径长 .
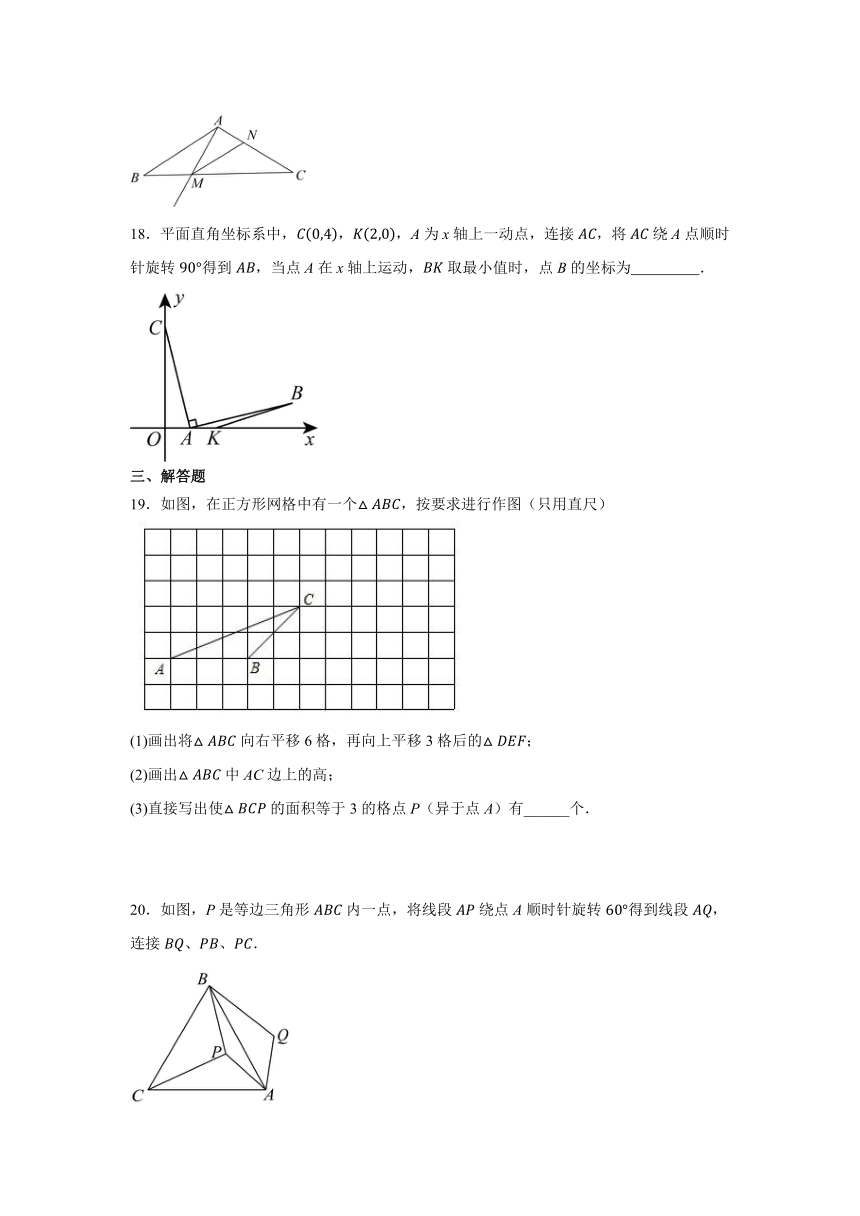
18.平面直角坐标系中,,,A为x轴上一动点,连接,将绕A点顺时针旋转得到,当点A在x轴上运动,取最小值时,点B的坐标为 .
三、解答题
19.如图,在正方形网格中有一个,按要求进行作图(只用直尺)
(1)画出将向右平移6格,再向上平移3格后的;
(2)画出中AC边上的高;
(3)直接写出使的面积等于3的格点P(异于点A)有______个.
20.如图,P是等边三角形内一点,将线段绕点A顺时针旋转得到线段,连接、、.
(1)求证:;
(2)若,,.求的面积.
21.如图(1),点D在等边三角形的边上,将绕点A旋转,使得旋转后点B的对应点为点C.
(1)在图(1)中画出旋转后的图形.
(2)小明是这样做的:如图(2),过点C画的平行线l,在l上取,连接,则即为旋转后的图形.你能说说小明这样做的道理吗?
22.如图1,在△ABC中,∠BAC=90°,AB=AC,点D在边AC上,CD⊥DE,且CD=DE,连接BE,取BE的中点F,连接DF.
(1)请直接写出∠ADF的度数及线段AD与DF的数量关系;
(2)将图1中的△CDE绕点C按逆时针旋转,
①如图2,(1)中∠ADF的度数及线段AD与DF的数量关系是否仍然成立?请说明理由;
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.
参考答案
1.C
2.A
3.C
4.A
5.A
6.B
7.D
8.C
9.C
10.D
11.60
12.(0,6).
13.
14.
15.90
16.60°.
17.9
18.
19.(1)解:作出△ABC的三个顶点向右平移6格,再向上平移3格后的对应点D、E、F,然后顺次连接这三个点,即为所求,如图所示:
(2)过点B作出垂直AC的直线,交AC于点H,则BH即为所求,如图所示:
(3)因为,所以过点A作BC的平行线,此平行线所过的格点,与B、C组成的三角形面积与△ABC的面积相等,即为3,符合要求;在BC右侧,作BC的平行线,且到BC的距离与A到BC的距离相等时,此平行线所过的格点,符合要求,如图所示:
根据图可知,符合要求的点共有14个.
20.(1)证明:是等边三角形,
,
由旋转可知,
,
,
在和中,
,
∴,
;
(2)解:如图,连接,
,
是等边三角形,则,
,
,
,,
,
,
∴,
,
∴,
作垂直于,交的延长线于,则,
∴,
∴.
21.(1)如图,为所作;
;
(2)∵为等边三角形,
∴,,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
∴即为旋转后的图形.
22.(1)解:∠ADF=45°,AD=DF,理由如下:
延长DF交AB于H,连接AF,
∵∠EDC=∠BAC=90°,
∴DE∥AB,
∴∠ABF=∠FED,
∵F是BE中点,
∴BF=EF,
又∠BFH=∠DFE,
∴△DEF≌△HBF,
∴BH=DE,HF=FD,
∵DE=CD,AB=AC,
∴BH=CD,AH=AD,
∴△ADH为等腰直角三角形,
∴∠ADF=45°,
又HF=FD,
∴AF⊥DH,
∴∠FAD=∠ADF=45°,
即△ADF为等腰直角三角形,
∴AD=DF;
(2)解:①结论仍然成立,∠ADF=45°,AD=DF,理由如下:
过B作DE的平行线交DF延长线于H,连接AH、AF,如图所示,
则∠FED=∠FBH,∠FHB=∠EFD,
∵F是BE中点,
∴BF=EF,
∴△DEF≌△HBF,
∴BH=DE,HF=FD,
∵DE=CD,
∴BH=CD,
延长ED交BC于M,
∵BH∥EM,∠EDC=90°,
∴∠HBC+∠DCB=∠DMC+∠DCB=90°,
又∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠HBA+∠DCB=45°,
∵∠ACD+∠DCB=45°,
∴∠HBA=∠ACD,
∴△ACD≌△ABH,
∴AD=AH,∠BAH=∠CAD,
∴∠CAD+∠DAB=∠BAH+∠DAB=90°,
即∠HAD=90°,
∴∠ADH=45°,
∵HF=DF,
∴AF⊥DF,即△ADF为等腰直角三角形,
∴AD=DF.
②由①知,S△ADF=DF2=AD2,
由旋转知,当A、C、D共线时,且D在A、C之间时,AD取最小值为3-1=2,
当A、C、D共线时,且C在A、D之间时,AD取最大值为3+1=4,
∴1≤S△ADF≤4.
学校:___________姓名:___________班级:___________
一、单选题
1.下列哪个图形是由图平移得到的是( )
A. B.
C. D.
2.将长度为3㎝的线段向下平移2㎝,则平移后的线段长度是( )
A.3㎝ B.2㎝ C.5㎝ D.1㎝
3.在平面直角坐标系中,将点向下平移2个单位长度得到点Q,若点Q在x轴上,则点P的坐标为( )
A. B. C. D.
4.如图(1)中,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图(1)作为“基本图形”绕着A点经过逆时针旋转得到图(2).两次旋转的角度分别为( )
A.45°,90° B.90°,45° C.60°,30° D.30°,60°
5.如图,在直角坐标系中,线段是将绕着点逆时针旋转一定角度后得到的的一部分,则点的对应点的坐标是( )
A.(-2,3) B.(-3,2) C.(-2,4) D.(-3,3)
6.如图是一块长方形的场地,长,宽,从、两处入口的中路宽都为,两小路汇合处路宽为,其余部分种植草坪,则草坪面积为( )
A.m2 B.m2 C.m2 D.m2
7.如图,在△ABC中,∠BAC=45°,AC=8,动点E从点A出发沿射线AB运动,连接CE,将CE绕点C顺时针旋转45°得到CF,连接AF,则△AFC的面积变化情况是( ).
A.先变大再变小 B.先变小再变大 C.逐渐变大 D.不变
8.如图,在等边中,,点在上,且,是上一动点,连接,将线段绕点逆时针旋转得到线段,若使点恰好落在上,则线段的长是( )
A.4 B.5 C.6 D.8
9.如图,点是等边三角形内一点,,,,则与的面积之和为( )
A. B. C. D.
10.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2026,则n的值为( )
A.407 B.406 C.405 D.404
二、填空题
11.如图是一个旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的度数至少为 °.
12.将点先向右平移2个单位,再向上平移3个单位后,则平移后点的坐标是 .
13.如图,边长为2的等边的边在x轴上,将绕原点O逆时针旋转得到三角形,则点的坐标为 .
14.如图,将绕着点逆时针旋转后得到,若,,则的度数为 .
15.如图,小正方形方格的边长都是1,点A、B、C、D、O都是小正方形的顶点.若COD是由AOB绕点O按顺时针方向旋转一次得到的,则至少需要旋转 °.
16.如图,是绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是 .
17.如图,在ABC中,AB=AC=6,∠B=30°,边BC上一个动点M从B运动到C,连AM,将射线AM绕M顺顺时针转30°交AC于N,则N的路径长 .
18.平面直角坐标系中,,,A为x轴上一动点,连接,将绕A点顺时针旋转得到,当点A在x轴上运动,取最小值时,点B的坐标为 .
三、解答题
19.如图,在正方形网格中有一个,按要求进行作图(只用直尺)
(1)画出将向右平移6格,再向上平移3格后的;
(2)画出中AC边上的高;
(3)直接写出使的面积等于3的格点P(异于点A)有______个.
20.如图,P是等边三角形内一点,将线段绕点A顺时针旋转得到线段,连接、、.
(1)求证:;
(2)若,,.求的面积.
21.如图(1),点D在等边三角形的边上,将绕点A旋转,使得旋转后点B的对应点为点C.
(1)在图(1)中画出旋转后的图形.
(2)小明是这样做的:如图(2),过点C画的平行线l,在l上取,连接,则即为旋转后的图形.你能说说小明这样做的道理吗?
22.如图1,在△ABC中,∠BAC=90°,AB=AC,点D在边AC上,CD⊥DE,且CD=DE,连接BE,取BE的中点F,连接DF.
(1)请直接写出∠ADF的度数及线段AD与DF的数量关系;
(2)将图1中的△CDE绕点C按逆时针旋转,
①如图2,(1)中∠ADF的度数及线段AD与DF的数量关系是否仍然成立?请说明理由;
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.
参考答案
1.C
2.A
3.C
4.A
5.A
6.B
7.D
8.C
9.C
10.D
11.60
12.(0,6).
13.
14.
15.90
16.60°.
17.9
18.
19.(1)解:作出△ABC的三个顶点向右平移6格,再向上平移3格后的对应点D、E、F,然后顺次连接这三个点,即为所求,如图所示:
(2)过点B作出垂直AC的直线,交AC于点H,则BH即为所求,如图所示:
(3)因为,所以过点A作BC的平行线,此平行线所过的格点,与B、C组成的三角形面积与△ABC的面积相等,即为3,符合要求;在BC右侧,作BC的平行线,且到BC的距离与A到BC的距离相等时,此平行线所过的格点,符合要求,如图所示:
根据图可知,符合要求的点共有14个.
20.(1)证明:是等边三角形,
,
由旋转可知,
,
,
在和中,
,
∴,
;
(2)解:如图,连接,
,
是等边三角形,则,
,
,
,,
,
,
∴,
,
∴,
作垂直于,交的延长线于,则,
∴,
∴.
21.(1)如图,为所作;
;
(2)∵为等边三角形,
∴,,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
∴即为旋转后的图形.
22.(1)解:∠ADF=45°,AD=DF,理由如下:
延长DF交AB于H,连接AF,
∵∠EDC=∠BAC=90°,
∴DE∥AB,
∴∠ABF=∠FED,
∵F是BE中点,
∴BF=EF,
又∠BFH=∠DFE,
∴△DEF≌△HBF,
∴BH=DE,HF=FD,
∵DE=CD,AB=AC,
∴BH=CD,AH=AD,
∴△ADH为等腰直角三角形,
∴∠ADF=45°,
又HF=FD,
∴AF⊥DH,
∴∠FAD=∠ADF=45°,
即△ADF为等腰直角三角形,
∴AD=DF;
(2)解:①结论仍然成立,∠ADF=45°,AD=DF,理由如下:
过B作DE的平行线交DF延长线于H,连接AH、AF,如图所示,
则∠FED=∠FBH,∠FHB=∠EFD,
∵F是BE中点,
∴BF=EF,
∴△DEF≌△HBF,
∴BH=DE,HF=FD,
∵DE=CD,
∴BH=CD,
延长ED交BC于M,
∵BH∥EM,∠EDC=90°,
∴∠HBC+∠DCB=∠DMC+∠DCB=90°,
又∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠HBA+∠DCB=45°,
∵∠ACD+∠DCB=45°,
∴∠HBA=∠ACD,
∴△ACD≌△ABH,
∴AD=AH,∠BAH=∠CAD,
∴∠CAD+∠DAB=∠BAH+∠DAB=90°,
即∠HAD=90°,
∴∠ADH=45°,
∵HF=DF,
∴AF⊥DF,即△ADF为等腰直角三角形,
∴AD=DF.
②由①知,S△ADF=DF2=AD2,
由旋转知,当A、C、D共线时,且D在A、C之间时,AD取最小值为3-1=2,
当A、C、D共线时,且C在A、D之间时,AD取最大值为3+1=4,
∴1≤S△ADF≤4.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
