2024-2025学年北师大版四年级数学下册第二单元认识三角形和四边形(情境题自测卷)(含解析)
文档属性
| 名称 | 2024-2025学年北师大版四年级数学下册第二单元认识三角形和四边形(情境题自测卷)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-23 00:00:00 | ||
图片预览




文档简介
/ 让教学更有效 精品试卷 | 数学学科
2024-2025学年北师大版四年级数学下册(情境题自测卷)
第二单元认识三角形和四边形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面方框内每组中的三个事物之间有相同的关系,那么下面选项中具有类似关系的一组是( )。
①水果,苹果,青苹果②动物,鸡,母鸡③交通工具,汽车,小轿车
A.四边形,长方形,梯形 B.四边形,三角形,平行四边形
C.四边形,平行四边形,长方形 D.四边形,正方形,梯形
2.小敏不小心将一块玻璃打碎成了如图的4块。为了能在商店配到一块与原来相同的平行四边形玻璃,他只带了两块碎玻璃,其编号应该是( )。
A.①和② B.②和③ C.③和④ D.②和④
3.下图是最负盛名的跪射俑,是保存最完整和唯一一尊未经人工修复的兵马俑,它的上体笔直挺立,下部是右膝、右足尖及左足抵地,三个支点形成三角形。这样设计的好处是( )。
A.高度更低 B.更节省材料 C.三角形具有稳定性 D.四边形具有稳定性
4.相机三脚架的结构设计(如图)是利用了三角形的( )。
A.稳定性 B.不稳定性 C.易变性
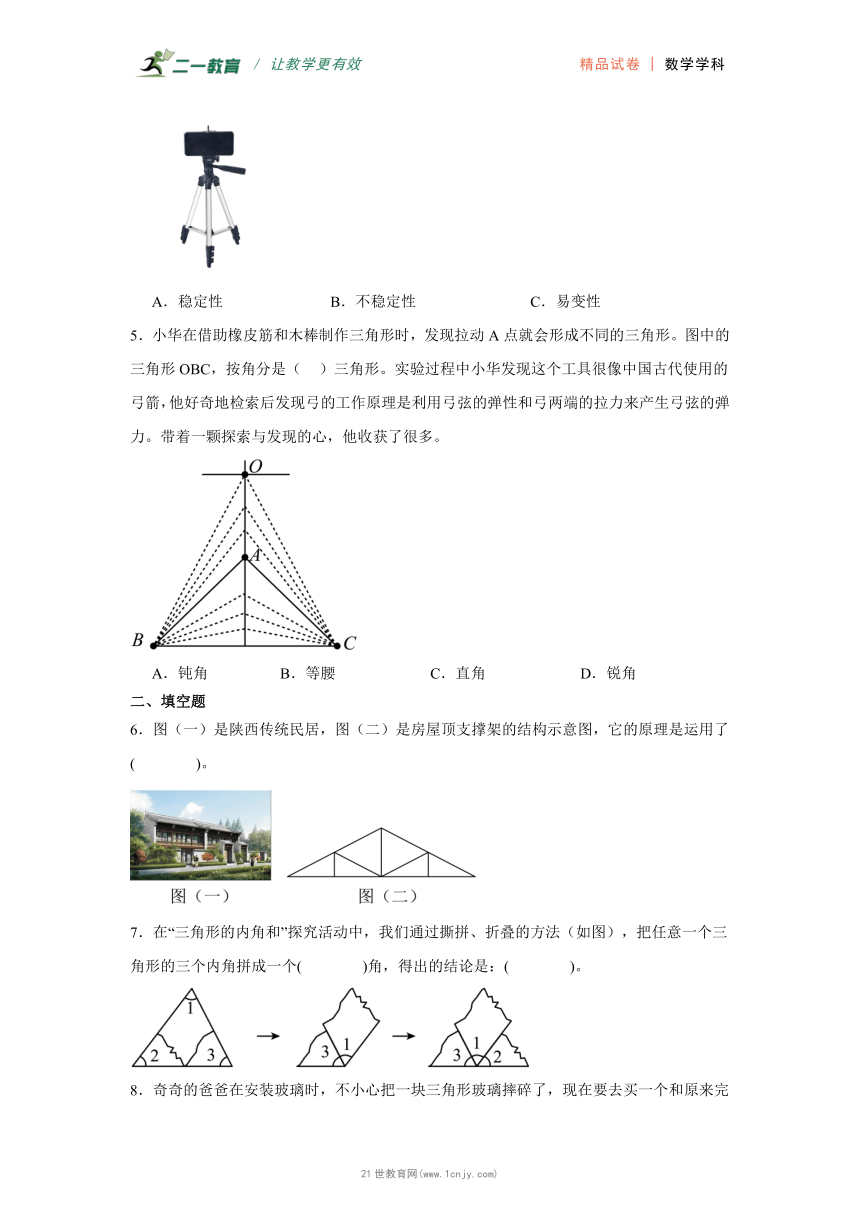
5.小华在借助橡皮筋和木棒制作三角形时,发现拉动A点就会形成不同的三角形。图中的三角形OBC,按角分是( )三角形。实验过程中小华发现这个工具很像中国古代使用的弓箭,他好奇地检索后发现弓的工作原理是利用弓弦的弹性和弓两端的拉力来产生弓弦的弹力。带着一颗探索与发现的心,他收获了很多。
A.钝角 B.等腰 C.直角 D.锐角
二、填空题
6.图(一)是陕西传统民居,图(二)是房屋顶支撑架的结构示意图,它的原理是运用了( )。
7.在“三角形的内角和”探究活动中,我们通过撕拼、折叠的方法(如图),把任意一个三角形的三个内角拼成一个( )角,得出的结论是:( )。
8.奇奇的爸爸在安装玻璃时,不小心把一块三角形玻璃摔碎了,现在要去买一个和原来完全相同的玻璃,只需要带图中第( )部分去就可以。
9.我们在研究三角形的内角和时,可以通过把三角形的三个内角对折去发现规律。按要求完成下题。
(1)请在图2中填出对应的角。
(2)对折之后,发现三角形的三个内角正好可以拼成一个 ,所以三角形的内角和是 。
10.张爷爷准备用一根14分米长的木条做一个等腰三角形风筝架子(边长都是整分米数),他可以有( )种做法。21*cnjy*com
11.生活中常见的伸缩门是应用了平行四边形的( )性,斜拉桥的外观设计则是应用了三角形的( )性。
12.三角形的内角和是多少度?
分析与解答:
(1)拿出你剪下来的三角形,把3个角剪下来,再把这3个角拼在一起,你发现了什么?
我们把3个角拼在一起,发现这3个角组成了一个( )角,所以,这个三角形的内角和是( )。
(2)拿出你剪下来的三角形,再按下面的方法折一折,你发现了什么?
我们把∠1、∠2、∠3按上图折,发现这3个角组成了一个( )角,所以,这个三角形的内角和是( )。
13.用同样长的小棒摆一摆,完成下表。
(1)3根小棒能否摆成一个三角形?它是什么三角形?
(2)4根小棒能否摆成一个三角形?5根、6根呢?
小棒根数 3 4 5 6
能摆成三角形吗
是什么三角形
14.如图所示,金字塔是古代埃及帝王的陵墓,它的样子像我国汉字中的“金”字。金字塔的基底是一个正方形,四个侧面都是等腰三角形,每个等腰三角形的顶角约是52°,它的底角大约是( )°。
15.图形的性质在生活中的应用非常广泛,手机支架是利用了三角形具有( )的性质;自动升降机是利用了( )容易变形的性质。
16.2009年成都崇州金鸡风筝扎制技术入选省级非物质文化遗产代表性项目。某同学准备用一根长16分米的竹条做一个等腰三角形的风筝架(边长是整分米数),一共有( )种不同的做法。
17.“儿童散学归来早,忙趁东风放纸鸢。”风筝是中国古代劳动人民发明的。在深圳风筝节上,有一个等腰三角形的风筝,其中两条边分别长1.8米和2米,这个等腰三角形风筝的周长是( )米或( )米。
三、解答题
18.儿童散学归来早,忙趁东风放纸鸢。”春天是放风筝的好时节,五一假期间爸爸给力力做了一个等腰三角形的风筝,这个等腰三角形风筝的底边长3厘米,一条腰长6厘米,这个等腰三角形周长是多少厘米?
19.周日,小夕一家外出散步,路上碰到了一些问题,请你帮助他们解决。
(1)小夕的爸爸身高1.82米,体重75千克,腿长约92厘米。小夕说她爸爸走一步可以迈2米。对于这种说法,你相信吗?请你从数学角度出发,写出结论,并解释理由。
(2)路上,他们路过文具店,小夕想买一面彩旗,彩旗的形状是等腰三角形。其中一个角是,想一想另外两个角分别是多少度?请列出所有的情况。
20.同学们正在进行“剪小棒摆三角形”的探索活动。一根长12厘米的小棒,如果先从4厘米处剪了一刀,作为三角形的一条边。要想摆成一个三角形,接下来可以从哪里剪开得到另两条边(边长都为整厘米)?请你先在图中用“|”标出剪的位置,再把思考过程写出来。图中每个“”都一样长。
21.淘气想给他的小狗做一个房子,房顶的框架要做成等腰三角形,现在已经有了两根分别长5分米的木料,做这个三角形框架的两腰。
(1)下面长度的木料中,________能做这个三角形框架的第三条边。
①12分米 ②10分米 ③9分米 ④4分米
(2)要使组成的三角形框架宽一些,选用哪一根木料?要使组成的三角形框架高一些。选用哪一根木料?(试着画出草图)
22.资料卡:
蚂蚁们的神奇旅行
红蚂蚁在A点处,以每小时20米的速度向正南方向爬行,经过2小时,它爬到了C点;黑蚂蚁以每小时40米的速度,从B点向正南方向爬行1小时后它爬到了D点。在下图中帮蚂蚁们完成这次旅行后,你将会有神奇的发现。
请根据以上材料中的信息并结合本单元所学知识解答下列各题。
考点1:平行与垂直
(1)红蚂蚁在A点处,以每小时20米的速度向正南方向爬行,经过2小时,它爬到了哪里?用C点标出它的位置。
(2)黑蚂蚁以每小时40米的速度,从B点向正南方向爬行1小时后它爬到哪里?用D点标出它的位置。
(3)黑蚂蚁爬到D点后又向正西方向爬行了1小时30分,爬到C点了吗,写出你的理由。
(4)黑蚂蚁一共爬行了多少米?
(5)用红色笔画一画红蚂蚁和黑蚂蚁爬行的路线,它们所爬行的每条路线和直线AB各是什么关系?
(6)如果AC垂直于AB,BD垂直于AB,那么AC、BD两条直线( )。
A.相交 B.互相平行 C.互相垂直
(7)如果同一平面内的两条直线和同一条直线平行,这两条直线( )。
A.互相垂直 B.互相平行 C.不一定是平行线
(8)过点P作AB的垂线段,垂足为O。
(9)连接PA、PB、PO、这三条线段中最短的是( )。
(10)过点P分别作AD的垂线段,垂足为M。
(11)A、B、C、D四个点组成了什么图形?说说你的理由。
考点2:平行四边形和梯形的认识
(12)以AB为底,以PO为高,画出一个平行四边形,这样的平行四边形最多可以画( )个。
(13)请画一个与平行四边形等高的梯形,并标出它的上底、下底和腰。
(14)在画成的梯形中画一条线段,把其分成一个平行四边形和一个梯形。
(15)这个单元我们学习了长方形、正方形、平行四边形和梯形,它们都属于四边形,相互之间联系又有区别,请你选择一个符合的条件,把序号写在括号里。
A.对边相等 B.两组对边互相平行 C.邻边相等
D.只有一组对边互相平行 E.邻边互相垂直 F.上底和下底相等
《2024-2025学年北师大版四年级数学下册第二单元认识三角形和四边形(情境题自测卷)》参考答案
1.C
【分析】由题意可知,方框内每组中的三个事物之间的共同点就是前者和后者之间都有包含关系,前者都包含了后者。据此选择。21教育网
【详解】A.长方形属于四边形,四边形包含了长方形,但梯形不属于长方形,所以长方形没有包含梯形。不符合题意。www-2-1-cnjy-com
B.三角形不属于四边形,前者没有包含后者。不符合题意。
C.平行四边形属于四边形,前者包含后者,长方形属于特殊的平行四边形,前者包含后者。符合题意。
D.正方形属于四边形,前者包含后者,但梯形不属于正方形,前者没有包含后者。不符合题意。
故答案为:C
2.D
【分析】平行四边形对边平行且相等,对角相等,根据平行四边形的定义和判定方法直接解答。
【详解】只有②和④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点。
故答案为:D
3.C
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造。据此选择即可。
【详解】这样设计的好处是三角形具有稳定性。
故答案为:C
4.A
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点,生活中很多物品的设计都利用这一特性设计的,据此作答。
【详解】根据解析可知,相机三脚架做成了三角形,利用了三角形的稳定性特点。
故答案为:A
5.D
【分析】大于0°小于90°的叫做锐角,等于90°的叫做直角,大于90°小于180°的叫做钝角。根据三角形的分类,按角分:分为锐角三角形,直角三角形和钝角三角形;3个角都是锐角的三角形是锐角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形;根据图示,三角形ABC是一个等腰直角三角形,顶角A为直角,等腰三角形的两个底角相等,又根据三角形内角和等于180°,(180°-90°)÷2=45°即∠B=∠C=45°,小华拉动A点到O点,顶角A变小,角B和角C度数变大,且三角形OBC的3个角均小于90°,所以三角形OBC,按角分是锐角三角形。
【详解】由分析可得,小华在借助橡皮筋和木棒制作三角形时,发现拉动A点就会形成不同的三角形。图中的三角形OBC,按角分是锐角三角形。
故答案为:D
6.三角形具有稳定性
【分析】三角形稳定性是指三角形三边长度一定时,它的形状,大小就不变了,生活中常运用三角形稳定性解决实际问题。
【详解】房屋顶支撑架的结构是三角形,它的原理是运用了三角形具有稳定性。
7. 平 任意一个三角形的内角和都是
【分析】在探究三角形的内角和时,我们可以把三角形的三个角剪下来,拼成一个平角,说明三角形的内角和是180度。
【详解】根据分析可知,把任意一个三角形的三个内角拼成一个平角,得出的结论是:任意一个三角形的内角和都是。
8.③
【分析】根据三角形的特性,只要确定三角形的一条边和两个角,就能确定这个三角形的形状,据此作答。
【详解】第①部分仅保留了原三角形的一个角和部分边,所以不能确定原来三角形的形状;
第②部分仅保留了原三角形的部分边,所以不能确定原来三角形的形状;
第③部分保留了原三角形的两个角还保留了其中一个边,所以可以确定原来三角形的形状。
因此,只需要带图中第③部分去就可以。
9.(1)见详解
(2)平角,180°
【分析】(1)根据对折三角形的过程及对称的特点,对折后三个角与原方向是相反的,即∠1顶点向下,∠2顶点向左,∠3顶点向右,据此在图2中填出对应的角即可;
(2)根据对折后的图,发现三角形的三个内角正好在一条直线上,即拼成了一个平角,平角度数是180°,所以三角形的内角和是180°。据此解答。21·世纪*教育网
【详解】(1)
(2)对折之后,发现三角形的三个内角正好可以拼成一个平角,所以三角形的内角和是180°。
10.3
【分析】张爷爷准备用一根14分米长的木条做一个等腰三角形风筝架子,即14分米是三角形的周长。14分米可分为的数字种类有:1,1,12;2,2,10;3,3,8;4,4,6;5,5,4;6,6,2。再根据三角形的任意两边之和大于第三边进行选择即可。
【详解】(14-2)÷2
=12÷2
=6(分米)
(14-4)÷2
=10÷2
=5(分米)
(14-6)÷2
=8÷2
=4(分米)
(14-8)÷2
=6÷2
=3(分米)
(14-10)÷2
=4÷2
=2(分米)
(14-12)÷2
=2÷2
=1(分米)
1+1<12;2+2<10;3+3<8;4+4>6;4+5>5;6+2>6
根据三角形三边关系可知:符合题意的是4,4,6;5,5,4;6,6,2。总共有3种做法。
【点睛】明确三角形的任意两边之和大于第三边是解题的关键。
11. 不稳定 稳定
【分析】平行四边形容易变形,也就是具有不稳定性;三角形具有稳定性,不容易变形。据此解答。
【详解】由分析可知:生活中常见的伸缩门是应用了平行四边形的不稳定性,斜拉桥的外观设计则是应用了三角形的稳定性。21*cnjy*com
12.(1) 平 180°
(2) 平 180°
【分析】(1)将这3个内角拼在一起,可以拼成一个平角,平角是180°的角,所以三角形的内角和是180°。
(2)同样道理,将∠1、∠2、∠3这3个角拼在一起,也可以拼成一个平角,能得出三角形的内角和是180°。
【详解】(1)我们把3个角拼在一起,发现这3个角组成了一个平角,所以,这个三角形的内角和是180°。
(2)我们把∠1、∠2、∠3按上图折,发现这3个角组成了一个平角,所以,这个三角形的内角和是180°。【版权所有:21教育】
【点睛】本题考查三角形内角和的定理,需熟练掌握。
13.见详解
【分析】三角形按边来分,分为普通三角形、等腰三角形和等边三角形。有两条边相等的三角形叫作等腰三角形,三条边都相等的三角形叫作等边三角形。
(1)三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)。经过尝试发现,3根同样长的小棒可以拼成一个等边三角形。
(2)尝试用4根小棒、5根小棒、6根小棒去摆成三角形,然后判断其是否能摆成三角形即可。
【详解】
(1)
故3根小棒能摆成一个等边三角形。
(2)
由图可知,4根小棒不能摆成一个三角形。
由图可知,5根小棒可以摆成一个等腰三角形。
由图可知,6根小棒可以摆成一个等边三角形。
小棒根数 3 4 5 6
能摆成三角形吗 能 不能 能 能
是什么三角形 等边三角形 ———— 等腰三角形 等边三角形
14.64
【分析】等腰三角形两个底角的度数相同,三角形内角和为180°,用180°-52°再除以2即可求出它的底角大约是多少度。21·cn·jy·com
【详解】(180°-52°)÷2
=128°÷2
=64°
每个等腰三角形的顶角约是52°,它的底角大约是64°。
15. 稳定 平行四边形
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,三角形具有稳定性,不容易变形,平行四边形不稳定,容易变形。据此解答即可。
【详解】图形的性质在生活中的应用非常广泛,手机支架是利用了三角形具有稳定的性质;自动升降机是利用了平行四边形容易变形的性质。【来源:21·世纪·教育·网】
16.3
【分析】等腰三角形周长为16分米,它的两条边为腰一样长,把16分成两个相等的数和第三个数的和为16,必须是整分米数,则第三边用偶数试,再根据三角形三边关系:两边之和大于第三边,两边之差小于第三边判断符合围成三角形的方法。
【详解】一边为2分米,腰为(16-2)÷2=7(分米),7+2>7,7-2<7符合;
一边为4分米,腰为(16-4)÷2=6(分米),6+4>6,6-4<6符合;
一边为6分米,腰为(16-6)÷2=5(分米),5+5>6,6-5<5符合;
一边为8分米,腰为(16-8)÷2=4(分米),4+4=8,不符合;
一边为10分米,腰为(16-10)÷2=3(分米),3+3<10,不符合;
一边为12分米,腰为(16-12)÷2=2(分米),2+2<12,不符合;
一边为14分米,腰为(16-14)÷2=1(分米),1+1<14,不符合;
可选用三边长为:
7分米,7分米,2分米;
6分米,6分米,4分米;
5分米,5分米,6分米;
一共有3种不同的做法。
17. 5.6 5.8
【分析】等腰三角形有两条边长相等,根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,先判断三条边的长度,相加即为周长,据此填空即可。
【详解】当腰为1.8米时:1.8+2=3.8(米),3.8米>1.8米,2-1.8=0.2(米),0.2米<1.8米,能构成三角形,1.8+1.8+2=3.6+2=5.6(米);【出处:21教育名师】
当腰是2米时:1.8+2=3.8(米),3.8米>2米,2-1.8=0.2(米),0.2米<2米,能构成三角形,1.8+2+2=3.8+2=5.8(米)。
这个等腰三角形风筝的周长是5.6米或5.8米。
18.15厘米
【分析】等腰三角形的两条腰的长度相等。由题意得,等腰三角形风筝的底边长3厘米,一条腰长6厘米,那么另一条腰也长6厘米,直接把这三条边的长度加起来即可算出这个等腰三角形的周长。
【详解】3+6+6
=9+6
=15(厘米)
答:这个等腰三角形周长是15厘米。
19.(1)不相信;理由见详解;(2)、或、。
【分析】(1)依据三角形的任意两边之和大于第三边,腿长约92厘米,走一步两腿和地面形成一个三角形,两腿的长度和要大于一步的距离,先求出92与92的和,再根据1米=100厘米,将2米的单位化为厘米是200厘米,最后与前面所得的和比较即可。
(2)已知给出了一个内角是,没有明确是顶角还是底角,所以要进行分类讨论根据三角形的内角和是180°,当顶角是70°时,先求出180°减70°的差,因为等腰三角形两个底角相等,再用这个差即可求出底角的度数;当底角是70°时,用180°减70°,再减70°,即可求出顶角的度数。
【详解】(1)不相信。
92(厘米)
2米厘米
184厘米厘米
答:不符合三角形的任意两边之和大于第三边,所以小夕说她爸爸走一步能迈2米这种说法不可信。
(2)分情况讨论:
①若等腰三角形的顶角为时;
(180°-70°)÷2
=110°÷2
=55°
②若等腰三角形的底角为时;
180°-70°-70°
=110°-70°
=40°
答:这个等腰三角形另外两个角分别是、或、。
20.见详解
【分析】根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,先从4厘米处剪了一刀,则有一条边长是4厘米,另外两条边长之和为12-4=8(厘米),8>4,所以只需要另外两条边长之差小于4厘米即可摆成三角形,据此解答即可。
【详解】12-4=8(厘米)
当另外两条边长为1厘米和7厘米时:7-1=6(厘米),6>4,不能围成三角形;
2厘米和6厘米:6-2=4(厘米),不能围成三角形;
3厘米和5厘米:5-3=2(厘米),2<4,可以围成三角形。
4+3=7(厘米),4+5=9(厘米)
答:可以从7厘米或9厘米处剪开得到另两条边。
如图:或
21.(1)③和④;(2)见详解
【分析】(1)三角形任意两边之和大于第三边,任意两边之差小于第三边,据此即可解答。
(2)根据等腰三角形的特点可知,要使组成的三角形框架宽一些,底边就要选长一些的木料,要使组成的三角形框架高一些,底边就要选短一些的木料,据此画图即可。
【详解】(1)5+5=10(分米)
5-5=0(分米)
0分米<第三条边<10分米
下面长度的木料中,③和④能做这个三角形框架的第三条边。
(2)要使组成的三角形框架宽一些,选用9分米的木料;要使组成的三角形框架高一些,选用4分米的木料,如下图。www.21-cn-jy.com
【点睛】本题主要考查学生对三角形三边间关系和三角形特点的掌握。
22.(1)见详解;
(2)见详解;
(3)爬到了;因为黑蚂蚁向正西爬了60米,即向左爬了6格,刚好到C点。
(4)100米;
(5)AC垂直AB;DB垂直AB;DC平行AB;
(6)B;
(7)B;
(8)见详解;
(9)PO;
(10)见详解;
(11)长方形;由四条边围成,两组对边互相平行且相等,四个角都是直角的四边形是长方形;
(12)图见详解;无数;
(13)见详解;
(14)见详解;
(15)见详解;
【分析】由图可知,每格边长代表10米。
(1)根据路程=时间×速度,用20乘2求出红蚂蚁爬行的路程。用路程除以10得到红蚂蚁向正南爬的格数,即红蚂蚁向下爬了几格,据此解答。21cnjy.com
(2)根据路程=时间×速度,用40乘1求出黑蚂蚁爬行的路程。用路程除以10得到黑蚂蚁向正南爬的格数,即黑蚂蚁向下爬了几格,据此解答。2-1-c-n-j-y
(3)根据路程=时间×速度,先求出1小时黑蚂蚁爬(40×1)米,再求出30分钟爬(40÷2)米,求出黑蚂蚁1小时30分钟一共爬行的路程。用路程除以10得到黑蚂蚁向正西爬的格数,即黑蚂蚁向左爬了几格,跟C点位置相比较,据此解答。【来源:21cnj*y.co*m】
(4)将(2)、(3)小问求出的路程相加,得到黑蚂蚁一共爬行的路程,据此解答。
(5)平行:是指在同一个平面内永远不会相交的两条直线
垂直:是指形成直角的两条直线。据此解答。
(6)在同一平面内,当不相交也不重合的两条直线都与第三条直线互相垂直,这两条直线互相平行。据此解答。21教育名师原创作品
(7)在同一平面内,当不重合且不相交的两条直线都与第三条直线互相平行,这两条直线也互相平行。据此解答。
(8)过P点作垂线的方法:先把三角尺的一条直角边与AB重合;沿着直线移动三角尺,使P点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号,垂足为O点。据此解答。
(9)点到直线的距离,垂线段最短。据此解答。
(10)过P点作垂线的方法:先把三角尺的一条直角边与AD重合;沿着直线移动三角尺,使P点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号,垂足为M点。据此解答。
(11)长方形:由四条边围成,两组对边互相平行且相等,四个角都是直角的四边形。据此解答。
(12)只要过点P画线段AB的平行线段,且长度与线段AB相等,可以画无数个平行四边形。据此解答。
(13)根据梯形的定义解答,注意作图后要标上底和高。据此解答。
(14)从梯形的上底向下底画一条与梯形的腰平行的线段即可。据此解答。
(15)平行四边形:两组对边分别平行的四边形;
梯形:只有一组对边平行的四边形;
长方形:四个角都是直角的平行四边形;
正方形:四条边都相等的长方形;据此解答。
【详解】(1)20×2=40(米) 40÷10=4(格)
红蚂蚁向下爬行4格
如图:
(2)40×1=40(米) 40÷10=4(格)
黑蚂蚁向下爬行4格
如图:
(3)40×1=40(米) 40÷2=20(米)
40+20=60(米) 60÷10=6(格)
如图:
爬到了;因为黑蚂蚁向正西爬了60米,即向左爬了6格,刚好到C点。
(4)40+60=100(米)
(5)AC垂直AB;DB垂直AB;DC平行AB;
(6)在同一平面内,几步相交也不重合的两条直线都与第三条直线互相垂直,这两条直线互相平行。
故答案为:B
(7)在同一平面内,当不重合且不相交的两条直线都与第三条直线互相平行,这两条直线也互相平行。
故答案为:B
(8)如图:
(9)点到直线的距离,垂线段最短。PO垂直AB
连接PA、PB、PO、这三条线段中最短的是( PO )。
(10)如图:
(11)长方形;由四条边围成,两组对边互相平行且相等,四个角都是直角的四边形是长方形;
(12)以AB为底,以PO为高,画出一个平行四边形,这样的平行四边形最多可以画( 无数 )个。
如图:(画法不唯一)
(13)如图:画法不唯一)
(14)如图:(画法不唯一)
(15)这个单元我们学习了长方形、正方形、平行四边形和梯形,它们都属于四边形,相互之间联系又有区别,请你选择一个符合的条件,把序号写在括号里。
A.对边相等 B.两组对边互相平行 C.邻边相等21世纪教育网版权所有
D.只有一组对边互相平行 E.邻边互相垂直 F.上底和下底相等
【点睛】本题考查的是平行垂直、长方形、正方形、平行四边形和梯形的定义以及它们的特征,解答本题的关键是牢固掌握定义,以及平行四边形和梯形高的画法,本题培养学生记忆能力和解决问题的能力。2·1·c·n·j·y
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
2024-2025学年北师大版四年级数学下册(情境题自测卷)
第二单元认识三角形和四边形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面方框内每组中的三个事物之间有相同的关系,那么下面选项中具有类似关系的一组是( )。
①水果,苹果,青苹果②动物,鸡,母鸡③交通工具,汽车,小轿车
A.四边形,长方形,梯形 B.四边形,三角形,平行四边形
C.四边形,平行四边形,长方形 D.四边形,正方形,梯形
2.小敏不小心将一块玻璃打碎成了如图的4块。为了能在商店配到一块与原来相同的平行四边形玻璃,他只带了两块碎玻璃,其编号应该是( )。
A.①和② B.②和③ C.③和④ D.②和④
3.下图是最负盛名的跪射俑,是保存最完整和唯一一尊未经人工修复的兵马俑,它的上体笔直挺立,下部是右膝、右足尖及左足抵地,三个支点形成三角形。这样设计的好处是( )。
A.高度更低 B.更节省材料 C.三角形具有稳定性 D.四边形具有稳定性
4.相机三脚架的结构设计(如图)是利用了三角形的( )。
A.稳定性 B.不稳定性 C.易变性
5.小华在借助橡皮筋和木棒制作三角形时,发现拉动A点就会形成不同的三角形。图中的三角形OBC,按角分是( )三角形。实验过程中小华发现这个工具很像中国古代使用的弓箭,他好奇地检索后发现弓的工作原理是利用弓弦的弹性和弓两端的拉力来产生弓弦的弹力。带着一颗探索与发现的心,他收获了很多。
A.钝角 B.等腰 C.直角 D.锐角
二、填空题
6.图(一)是陕西传统民居,图(二)是房屋顶支撑架的结构示意图,它的原理是运用了( )。
7.在“三角形的内角和”探究活动中,我们通过撕拼、折叠的方法(如图),把任意一个三角形的三个内角拼成一个( )角,得出的结论是:( )。
8.奇奇的爸爸在安装玻璃时,不小心把一块三角形玻璃摔碎了,现在要去买一个和原来完全相同的玻璃,只需要带图中第( )部分去就可以。
9.我们在研究三角形的内角和时,可以通过把三角形的三个内角对折去发现规律。按要求完成下题。
(1)请在图2中填出对应的角。
(2)对折之后,发现三角形的三个内角正好可以拼成一个 ,所以三角形的内角和是 。
10.张爷爷准备用一根14分米长的木条做一个等腰三角形风筝架子(边长都是整分米数),他可以有( )种做法。21*cnjy*com
11.生活中常见的伸缩门是应用了平行四边形的( )性,斜拉桥的外观设计则是应用了三角形的( )性。
12.三角形的内角和是多少度?
分析与解答:
(1)拿出你剪下来的三角形,把3个角剪下来,再把这3个角拼在一起,你发现了什么?
我们把3个角拼在一起,发现这3个角组成了一个( )角,所以,这个三角形的内角和是( )。
(2)拿出你剪下来的三角形,再按下面的方法折一折,你发现了什么?
我们把∠1、∠2、∠3按上图折,发现这3个角组成了一个( )角,所以,这个三角形的内角和是( )。
13.用同样长的小棒摆一摆,完成下表。
(1)3根小棒能否摆成一个三角形?它是什么三角形?
(2)4根小棒能否摆成一个三角形?5根、6根呢?
小棒根数 3 4 5 6
能摆成三角形吗
是什么三角形
14.如图所示,金字塔是古代埃及帝王的陵墓,它的样子像我国汉字中的“金”字。金字塔的基底是一个正方形,四个侧面都是等腰三角形,每个等腰三角形的顶角约是52°,它的底角大约是( )°。
15.图形的性质在生活中的应用非常广泛,手机支架是利用了三角形具有( )的性质;自动升降机是利用了( )容易变形的性质。
16.2009年成都崇州金鸡风筝扎制技术入选省级非物质文化遗产代表性项目。某同学准备用一根长16分米的竹条做一个等腰三角形的风筝架(边长是整分米数),一共有( )种不同的做法。
17.“儿童散学归来早,忙趁东风放纸鸢。”风筝是中国古代劳动人民发明的。在深圳风筝节上,有一个等腰三角形的风筝,其中两条边分别长1.8米和2米,这个等腰三角形风筝的周长是( )米或( )米。
三、解答题
18.儿童散学归来早,忙趁东风放纸鸢。”春天是放风筝的好时节,五一假期间爸爸给力力做了一个等腰三角形的风筝,这个等腰三角形风筝的底边长3厘米,一条腰长6厘米,这个等腰三角形周长是多少厘米?
19.周日,小夕一家外出散步,路上碰到了一些问题,请你帮助他们解决。
(1)小夕的爸爸身高1.82米,体重75千克,腿长约92厘米。小夕说她爸爸走一步可以迈2米。对于这种说法,你相信吗?请你从数学角度出发,写出结论,并解释理由。
(2)路上,他们路过文具店,小夕想买一面彩旗,彩旗的形状是等腰三角形。其中一个角是,想一想另外两个角分别是多少度?请列出所有的情况。
20.同学们正在进行“剪小棒摆三角形”的探索活动。一根长12厘米的小棒,如果先从4厘米处剪了一刀,作为三角形的一条边。要想摆成一个三角形,接下来可以从哪里剪开得到另两条边(边长都为整厘米)?请你先在图中用“|”标出剪的位置,再把思考过程写出来。图中每个“”都一样长。
21.淘气想给他的小狗做一个房子,房顶的框架要做成等腰三角形,现在已经有了两根分别长5分米的木料,做这个三角形框架的两腰。
(1)下面长度的木料中,________能做这个三角形框架的第三条边。
①12分米 ②10分米 ③9分米 ④4分米
(2)要使组成的三角形框架宽一些,选用哪一根木料?要使组成的三角形框架高一些。选用哪一根木料?(试着画出草图)
22.资料卡:
蚂蚁们的神奇旅行
红蚂蚁在A点处,以每小时20米的速度向正南方向爬行,经过2小时,它爬到了C点;黑蚂蚁以每小时40米的速度,从B点向正南方向爬行1小时后它爬到了D点。在下图中帮蚂蚁们完成这次旅行后,你将会有神奇的发现。
请根据以上材料中的信息并结合本单元所学知识解答下列各题。
考点1:平行与垂直
(1)红蚂蚁在A点处,以每小时20米的速度向正南方向爬行,经过2小时,它爬到了哪里?用C点标出它的位置。
(2)黑蚂蚁以每小时40米的速度,从B点向正南方向爬行1小时后它爬到哪里?用D点标出它的位置。
(3)黑蚂蚁爬到D点后又向正西方向爬行了1小时30分,爬到C点了吗,写出你的理由。
(4)黑蚂蚁一共爬行了多少米?
(5)用红色笔画一画红蚂蚁和黑蚂蚁爬行的路线,它们所爬行的每条路线和直线AB各是什么关系?
(6)如果AC垂直于AB,BD垂直于AB,那么AC、BD两条直线( )。
A.相交 B.互相平行 C.互相垂直
(7)如果同一平面内的两条直线和同一条直线平行,这两条直线( )。
A.互相垂直 B.互相平行 C.不一定是平行线
(8)过点P作AB的垂线段,垂足为O。
(9)连接PA、PB、PO、这三条线段中最短的是( )。
(10)过点P分别作AD的垂线段,垂足为M。
(11)A、B、C、D四个点组成了什么图形?说说你的理由。
考点2:平行四边形和梯形的认识
(12)以AB为底,以PO为高,画出一个平行四边形,这样的平行四边形最多可以画( )个。
(13)请画一个与平行四边形等高的梯形,并标出它的上底、下底和腰。
(14)在画成的梯形中画一条线段,把其分成一个平行四边形和一个梯形。
(15)这个单元我们学习了长方形、正方形、平行四边形和梯形,它们都属于四边形,相互之间联系又有区别,请你选择一个符合的条件,把序号写在括号里。
A.对边相等 B.两组对边互相平行 C.邻边相等
D.只有一组对边互相平行 E.邻边互相垂直 F.上底和下底相等
《2024-2025学年北师大版四年级数学下册第二单元认识三角形和四边形(情境题自测卷)》参考答案
1.C
【分析】由题意可知,方框内每组中的三个事物之间的共同点就是前者和后者之间都有包含关系,前者都包含了后者。据此选择。21教育网
【详解】A.长方形属于四边形,四边形包含了长方形,但梯形不属于长方形,所以长方形没有包含梯形。不符合题意。www-2-1-cnjy-com
B.三角形不属于四边形,前者没有包含后者。不符合题意。
C.平行四边形属于四边形,前者包含后者,长方形属于特殊的平行四边形,前者包含后者。符合题意。
D.正方形属于四边形,前者包含后者,但梯形不属于正方形,前者没有包含后者。不符合题意。
故答案为:C
2.D
【分析】平行四边形对边平行且相等,对角相等,根据平行四边形的定义和判定方法直接解答。
【详解】只有②和④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点。
故答案为:D
3.C
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造。据此选择即可。
【详解】这样设计的好处是三角形具有稳定性。
故答案为:C
4.A
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点,生活中很多物品的设计都利用这一特性设计的,据此作答。
【详解】根据解析可知,相机三脚架做成了三角形,利用了三角形的稳定性特点。
故答案为:A
5.D
【分析】大于0°小于90°的叫做锐角,等于90°的叫做直角,大于90°小于180°的叫做钝角。根据三角形的分类,按角分:分为锐角三角形,直角三角形和钝角三角形;3个角都是锐角的三角形是锐角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形;根据图示,三角形ABC是一个等腰直角三角形,顶角A为直角,等腰三角形的两个底角相等,又根据三角形内角和等于180°,(180°-90°)÷2=45°即∠B=∠C=45°,小华拉动A点到O点,顶角A变小,角B和角C度数变大,且三角形OBC的3个角均小于90°,所以三角形OBC,按角分是锐角三角形。
【详解】由分析可得,小华在借助橡皮筋和木棒制作三角形时,发现拉动A点就会形成不同的三角形。图中的三角形OBC,按角分是锐角三角形。
故答案为:D
6.三角形具有稳定性
【分析】三角形稳定性是指三角形三边长度一定时,它的形状,大小就不变了,生活中常运用三角形稳定性解决实际问题。
【详解】房屋顶支撑架的结构是三角形,它的原理是运用了三角形具有稳定性。
7. 平 任意一个三角形的内角和都是
【分析】在探究三角形的内角和时,我们可以把三角形的三个角剪下来,拼成一个平角,说明三角形的内角和是180度。
【详解】根据分析可知,把任意一个三角形的三个内角拼成一个平角,得出的结论是:任意一个三角形的内角和都是。
8.③
【分析】根据三角形的特性,只要确定三角形的一条边和两个角,就能确定这个三角形的形状,据此作答。
【详解】第①部分仅保留了原三角形的一个角和部分边,所以不能确定原来三角形的形状;
第②部分仅保留了原三角形的部分边,所以不能确定原来三角形的形状;
第③部分保留了原三角形的两个角还保留了其中一个边,所以可以确定原来三角形的形状。
因此,只需要带图中第③部分去就可以。
9.(1)见详解
(2)平角,180°
【分析】(1)根据对折三角形的过程及对称的特点,对折后三个角与原方向是相反的,即∠1顶点向下,∠2顶点向左,∠3顶点向右,据此在图2中填出对应的角即可;
(2)根据对折后的图,发现三角形的三个内角正好在一条直线上,即拼成了一个平角,平角度数是180°,所以三角形的内角和是180°。据此解答。21·世纪*教育网
【详解】(1)
(2)对折之后,发现三角形的三个内角正好可以拼成一个平角,所以三角形的内角和是180°。
10.3
【分析】张爷爷准备用一根14分米长的木条做一个等腰三角形风筝架子,即14分米是三角形的周长。14分米可分为的数字种类有:1,1,12;2,2,10;3,3,8;4,4,6;5,5,4;6,6,2。再根据三角形的任意两边之和大于第三边进行选择即可。
【详解】(14-2)÷2
=12÷2
=6(分米)
(14-4)÷2
=10÷2
=5(分米)
(14-6)÷2
=8÷2
=4(分米)
(14-8)÷2
=6÷2
=3(分米)
(14-10)÷2
=4÷2
=2(分米)
(14-12)÷2
=2÷2
=1(分米)
1+1<12;2+2<10;3+3<8;4+4>6;4+5>5;6+2>6
根据三角形三边关系可知:符合题意的是4,4,6;5,5,4;6,6,2。总共有3种做法。
【点睛】明确三角形的任意两边之和大于第三边是解题的关键。
11. 不稳定 稳定
【分析】平行四边形容易变形,也就是具有不稳定性;三角形具有稳定性,不容易变形。据此解答。
【详解】由分析可知:生活中常见的伸缩门是应用了平行四边形的不稳定性,斜拉桥的外观设计则是应用了三角形的稳定性。21*cnjy*com
12.(1) 平 180°
(2) 平 180°
【分析】(1)将这3个内角拼在一起,可以拼成一个平角,平角是180°的角,所以三角形的内角和是180°。
(2)同样道理,将∠1、∠2、∠3这3个角拼在一起,也可以拼成一个平角,能得出三角形的内角和是180°。
【详解】(1)我们把3个角拼在一起,发现这3个角组成了一个平角,所以,这个三角形的内角和是180°。
(2)我们把∠1、∠2、∠3按上图折,发现这3个角组成了一个平角,所以,这个三角形的内角和是180°。【版权所有:21教育】
【点睛】本题考查三角形内角和的定理,需熟练掌握。
13.见详解
【分析】三角形按边来分,分为普通三角形、等腰三角形和等边三角形。有两条边相等的三角形叫作等腰三角形,三条边都相等的三角形叫作等边三角形。
(1)三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)。经过尝试发现,3根同样长的小棒可以拼成一个等边三角形。
(2)尝试用4根小棒、5根小棒、6根小棒去摆成三角形,然后判断其是否能摆成三角形即可。
【详解】
(1)
故3根小棒能摆成一个等边三角形。
(2)
由图可知,4根小棒不能摆成一个三角形。
由图可知,5根小棒可以摆成一个等腰三角形。
由图可知,6根小棒可以摆成一个等边三角形。
小棒根数 3 4 5 6
能摆成三角形吗 能 不能 能 能
是什么三角形 等边三角形 ———— 等腰三角形 等边三角形
14.64
【分析】等腰三角形两个底角的度数相同,三角形内角和为180°,用180°-52°再除以2即可求出它的底角大约是多少度。21·cn·jy·com
【详解】(180°-52°)÷2
=128°÷2
=64°
每个等腰三角形的顶角约是52°,它的底角大约是64°。
15. 稳定 平行四边形
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,三角形具有稳定性,不容易变形,平行四边形不稳定,容易变形。据此解答即可。
【详解】图形的性质在生活中的应用非常广泛,手机支架是利用了三角形具有稳定的性质;自动升降机是利用了平行四边形容易变形的性质。【来源:21·世纪·教育·网】
16.3
【分析】等腰三角形周长为16分米,它的两条边为腰一样长,把16分成两个相等的数和第三个数的和为16,必须是整分米数,则第三边用偶数试,再根据三角形三边关系:两边之和大于第三边,两边之差小于第三边判断符合围成三角形的方法。
【详解】一边为2分米,腰为(16-2)÷2=7(分米),7+2>7,7-2<7符合;
一边为4分米,腰为(16-4)÷2=6(分米),6+4>6,6-4<6符合;
一边为6分米,腰为(16-6)÷2=5(分米),5+5>6,6-5<5符合;
一边为8分米,腰为(16-8)÷2=4(分米),4+4=8,不符合;
一边为10分米,腰为(16-10)÷2=3(分米),3+3<10,不符合;
一边为12分米,腰为(16-12)÷2=2(分米),2+2<12,不符合;
一边为14分米,腰为(16-14)÷2=1(分米),1+1<14,不符合;
可选用三边长为:
7分米,7分米,2分米;
6分米,6分米,4分米;
5分米,5分米,6分米;
一共有3种不同的做法。
17. 5.6 5.8
【分析】等腰三角形有两条边长相等,根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,先判断三条边的长度,相加即为周长,据此填空即可。
【详解】当腰为1.8米时:1.8+2=3.8(米),3.8米>1.8米,2-1.8=0.2(米),0.2米<1.8米,能构成三角形,1.8+1.8+2=3.6+2=5.6(米);【出处:21教育名师】
当腰是2米时:1.8+2=3.8(米),3.8米>2米,2-1.8=0.2(米),0.2米<2米,能构成三角形,1.8+2+2=3.8+2=5.8(米)。
这个等腰三角形风筝的周长是5.6米或5.8米。
18.15厘米
【分析】等腰三角形的两条腰的长度相等。由题意得,等腰三角形风筝的底边长3厘米,一条腰长6厘米,那么另一条腰也长6厘米,直接把这三条边的长度加起来即可算出这个等腰三角形的周长。
【详解】3+6+6
=9+6
=15(厘米)
答:这个等腰三角形周长是15厘米。
19.(1)不相信;理由见详解;(2)、或、。
【分析】(1)依据三角形的任意两边之和大于第三边,腿长约92厘米,走一步两腿和地面形成一个三角形,两腿的长度和要大于一步的距离,先求出92与92的和,再根据1米=100厘米,将2米的单位化为厘米是200厘米,最后与前面所得的和比较即可。
(2)已知给出了一个内角是,没有明确是顶角还是底角,所以要进行分类讨论根据三角形的内角和是180°,当顶角是70°时,先求出180°减70°的差,因为等腰三角形两个底角相等,再用这个差即可求出底角的度数;当底角是70°时,用180°减70°,再减70°,即可求出顶角的度数。
【详解】(1)不相信。
92(厘米)
2米厘米
184厘米厘米
答:不符合三角形的任意两边之和大于第三边,所以小夕说她爸爸走一步能迈2米这种说法不可信。
(2)分情况讨论:
①若等腰三角形的顶角为时;
(180°-70°)÷2
=110°÷2
=55°
②若等腰三角形的底角为时;
180°-70°-70°
=110°-70°
=40°
答:这个等腰三角形另外两个角分别是、或、。
20.见详解
【分析】根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,先从4厘米处剪了一刀,则有一条边长是4厘米,另外两条边长之和为12-4=8(厘米),8>4,所以只需要另外两条边长之差小于4厘米即可摆成三角形,据此解答即可。
【详解】12-4=8(厘米)
当另外两条边长为1厘米和7厘米时:7-1=6(厘米),6>4,不能围成三角形;
2厘米和6厘米:6-2=4(厘米),不能围成三角形;
3厘米和5厘米:5-3=2(厘米),2<4,可以围成三角形。
4+3=7(厘米),4+5=9(厘米)
答:可以从7厘米或9厘米处剪开得到另两条边。
如图:或
21.(1)③和④;(2)见详解
【分析】(1)三角形任意两边之和大于第三边,任意两边之差小于第三边,据此即可解答。
(2)根据等腰三角形的特点可知,要使组成的三角形框架宽一些,底边就要选长一些的木料,要使组成的三角形框架高一些,底边就要选短一些的木料,据此画图即可。
【详解】(1)5+5=10(分米)
5-5=0(分米)
0分米<第三条边<10分米
下面长度的木料中,③和④能做这个三角形框架的第三条边。
(2)要使组成的三角形框架宽一些,选用9分米的木料;要使组成的三角形框架高一些,选用4分米的木料,如下图。www.21-cn-jy.com
【点睛】本题主要考查学生对三角形三边间关系和三角形特点的掌握。
22.(1)见详解;
(2)见详解;
(3)爬到了;因为黑蚂蚁向正西爬了60米,即向左爬了6格,刚好到C点。
(4)100米;
(5)AC垂直AB;DB垂直AB;DC平行AB;
(6)B;
(7)B;
(8)见详解;
(9)PO;
(10)见详解;
(11)长方形;由四条边围成,两组对边互相平行且相等,四个角都是直角的四边形是长方形;
(12)图见详解;无数;
(13)见详解;
(14)见详解;
(15)见详解;
【分析】由图可知,每格边长代表10米。
(1)根据路程=时间×速度,用20乘2求出红蚂蚁爬行的路程。用路程除以10得到红蚂蚁向正南爬的格数,即红蚂蚁向下爬了几格,据此解答。21cnjy.com
(2)根据路程=时间×速度,用40乘1求出黑蚂蚁爬行的路程。用路程除以10得到黑蚂蚁向正南爬的格数,即黑蚂蚁向下爬了几格,据此解答。2-1-c-n-j-y
(3)根据路程=时间×速度,先求出1小时黑蚂蚁爬(40×1)米,再求出30分钟爬(40÷2)米,求出黑蚂蚁1小时30分钟一共爬行的路程。用路程除以10得到黑蚂蚁向正西爬的格数,即黑蚂蚁向左爬了几格,跟C点位置相比较,据此解答。【来源:21cnj*y.co*m】
(4)将(2)、(3)小问求出的路程相加,得到黑蚂蚁一共爬行的路程,据此解答。
(5)平行:是指在同一个平面内永远不会相交的两条直线
垂直:是指形成直角的两条直线。据此解答。
(6)在同一平面内,当不相交也不重合的两条直线都与第三条直线互相垂直,这两条直线互相平行。据此解答。21教育名师原创作品
(7)在同一平面内,当不重合且不相交的两条直线都与第三条直线互相平行,这两条直线也互相平行。据此解答。
(8)过P点作垂线的方法:先把三角尺的一条直角边与AB重合;沿着直线移动三角尺,使P点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号,垂足为O点。据此解答。
(9)点到直线的距离,垂线段最短。据此解答。
(10)过P点作垂线的方法:先把三角尺的一条直角边与AD重合;沿着直线移动三角尺,使P点在三角尺的另一条直角边上。再沿三角尺的另一条直角边画一条直线,并画上垂直符号,垂足为M点。据此解答。
(11)长方形:由四条边围成,两组对边互相平行且相等,四个角都是直角的四边形。据此解答。
(12)只要过点P画线段AB的平行线段,且长度与线段AB相等,可以画无数个平行四边形。据此解答。
(13)根据梯形的定义解答,注意作图后要标上底和高。据此解答。
(14)从梯形的上底向下底画一条与梯形的腰平行的线段即可。据此解答。
(15)平行四边形:两组对边分别平行的四边形;
梯形:只有一组对边平行的四边形;
长方形:四个角都是直角的平行四边形;
正方形:四条边都相等的长方形;据此解答。
【详解】(1)20×2=40(米) 40÷10=4(格)
红蚂蚁向下爬行4格
如图:
(2)40×1=40(米) 40÷10=4(格)
黑蚂蚁向下爬行4格
如图:
(3)40×1=40(米) 40÷2=20(米)
40+20=60(米) 60÷10=6(格)
如图:
爬到了;因为黑蚂蚁向正西爬了60米,即向左爬了6格,刚好到C点。
(4)40+60=100(米)
(5)AC垂直AB;DB垂直AB;DC平行AB;
(6)在同一平面内,几步相交也不重合的两条直线都与第三条直线互相垂直,这两条直线互相平行。
故答案为:B
(7)在同一平面内,当不重合且不相交的两条直线都与第三条直线互相平行,这两条直线也互相平行。
故答案为:B
(8)如图:
(9)点到直线的距离,垂线段最短。PO垂直AB
连接PA、PB、PO、这三条线段中最短的是( PO )。
(10)如图:
(11)长方形;由四条边围成,两组对边互相平行且相等,四个角都是直角的四边形是长方形;
(12)以AB为底,以PO为高,画出一个平行四边形,这样的平行四边形最多可以画( 无数 )个。
如图:(画法不唯一)
(13)如图:画法不唯一)
(14)如图:(画法不唯一)
(15)这个单元我们学习了长方形、正方形、平行四边形和梯形,它们都属于四边形,相互之间联系又有区别,请你选择一个符合的条件,把序号写在括号里。
A.对边相等 B.两组对边互相平行 C.邻边相等21世纪教育网版权所有
D.只有一组对边互相平行 E.邻边互相垂直 F.上底和下底相等
【点睛】本题考查的是平行垂直、长方形、正方形、平行四边形和梯形的定义以及它们的特征,解答本题的关键是牢固掌握定义,以及平行四边形和梯形高的画法,本题培养学生记忆能力和解决问题的能力。2·1·c·n·j·y
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
