2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题(含解析) | 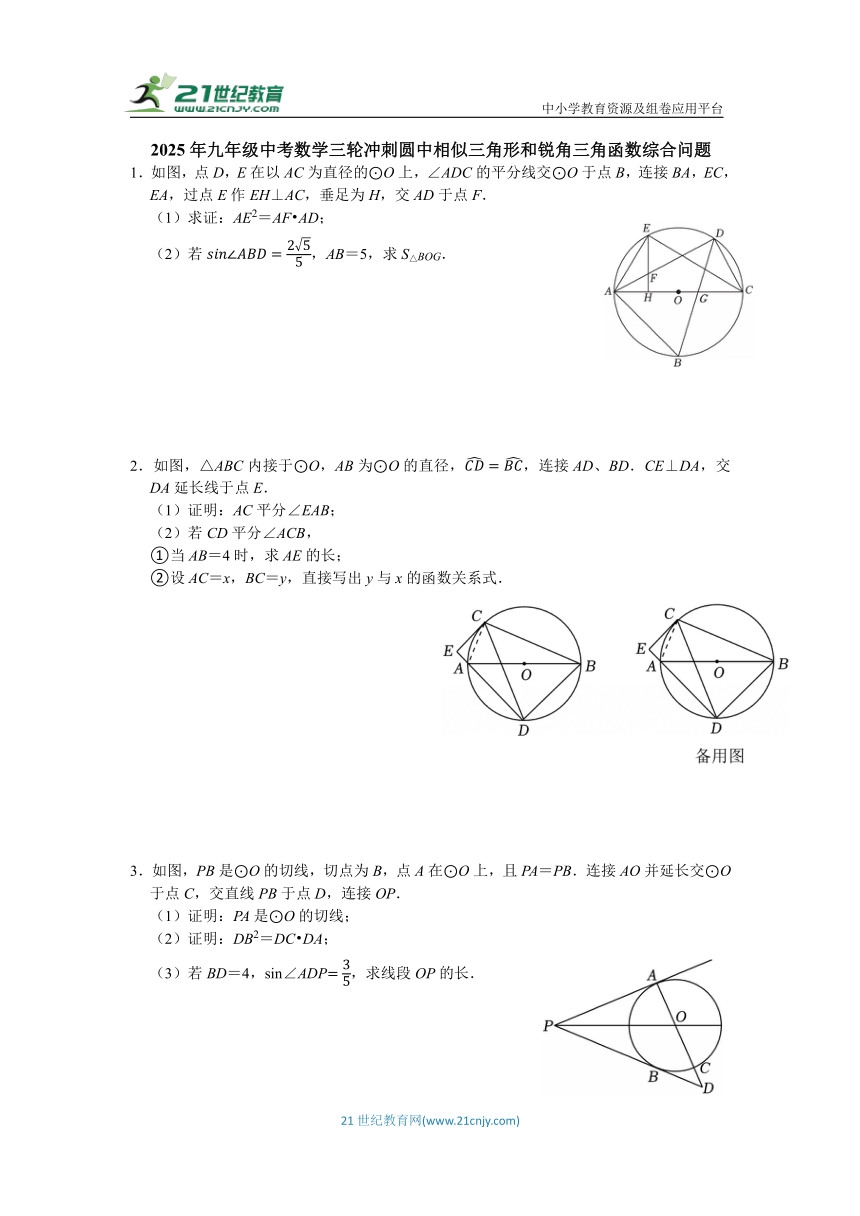 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 05:54:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题
1.如图,点D,E在以AC为直径的⊙O上,∠ADC的平分线交⊙O于点B,连接BA,EC,EA,过点E作EH⊥AC,垂足为H,交AD于点F.
(1)求证:AE2=AF AD;
(2)若,AB=5,求S△BOG.
2.如图,△ABC内接于⊙O,AB为⊙O的直径,,连接AD、BD.CE⊥DA,交DA延长线于点E.
(1)证明:AC平分∠EAB;
(2)若CD平分∠ACB,
①当AB=4时,求AE的长;
②设AC=x,BC=y,直接写出y与x的函数关系式.
3.如图,PB是⊙O的切线,切点为B,点A在⊙O上,且PA=PB.连接AO并延长交⊙O于点C,交直线PB于点D,连接OP.
(1)证明:PA是⊙O的切线;
(2)证明:DB2=DC DA;
(3)若BD=4,sin∠ADP,求线段OP的长.
4.如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F,CD=24,求⊙O的半径;
(3)请问的值为定值吗?若是,请写出计算过程,若不是,请说明理由.
5.如图,在△ABC中,∠C=90°,O为边AB上的一点,以O为圆心,OB为半径的圆与AC切于点E,与AB交于另一点D.
(1)求证:BE平分∠ABC;
(2)若BO=4,BE=6,求CE的长;
(3)在(2)的条件下,直接写出cosA的值.
6.已知,如图,线段AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH EA;
(3)若⊙O的半径为5,sinA,求BH的长.
7.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.AF=1,EF=2,
(1)求证:EF是⊙O切线;
(2)求sin∠F;
(3)求BD的值.
8.如图,△ADP是直角三角形,∠PAD=90°,以AD为直径作⊙O,与PD相交于点B,连接AB.
(1)尺规作图:在劣弧BD上取点C,使得弧AB=弧BC,连接AC,交BD于点E;
(2)在(1)的条件下,求证:△ABE∽△DBA;
(3)在(2)的条件下,连接CD,若E为BD的中点,求tan∠ADC的值.
9.如图,AB是⊙O的直径,C为⊙O上一点,连接AC,BC,延长AB至点D,使得∠DCB=∠CAB,点E为的中点,连接CE交AB于点F,连接BE.
(1)求证:DC为⊙O的切线;
(2)求证:△ACF∽△ECB;
(3)若,则直接写出CF CE= .
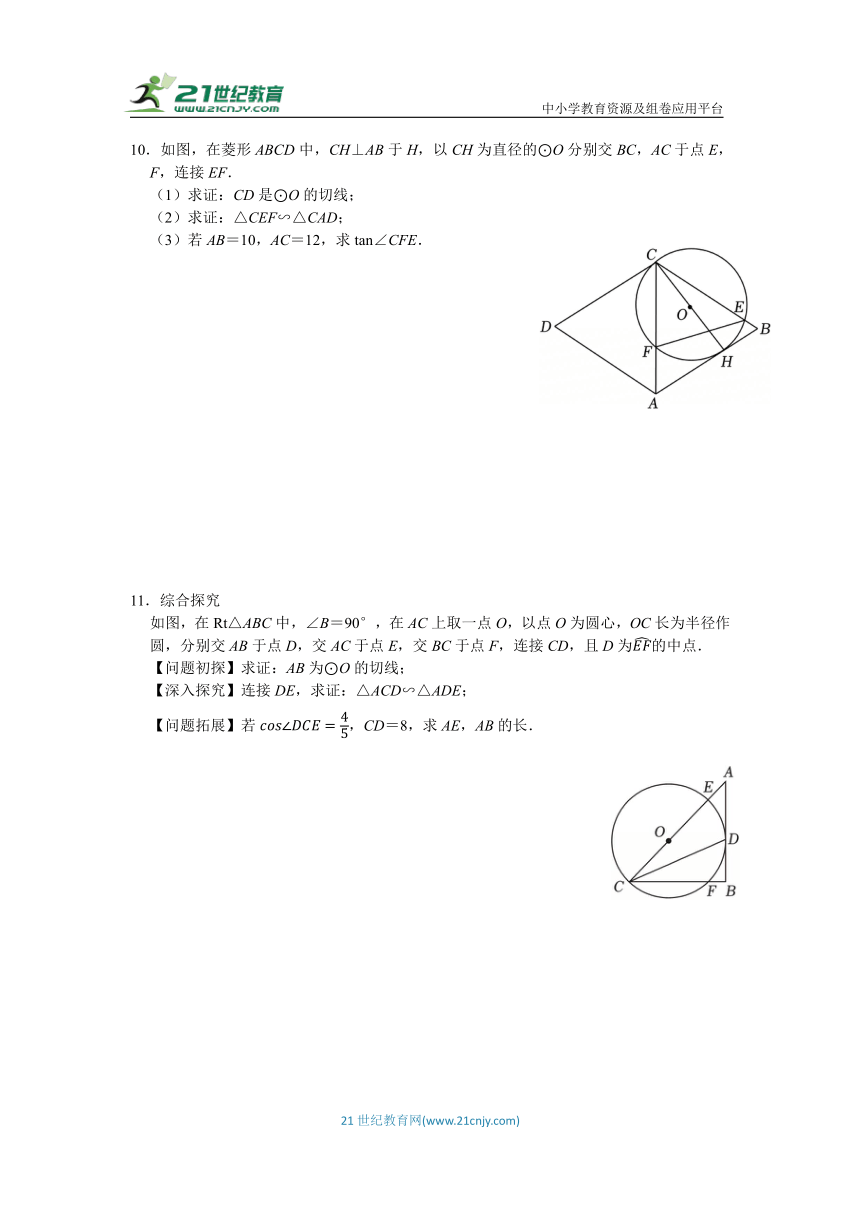
10.如图,在菱形ABCD中,CH⊥AB于H,以CH为直径的⊙O分别交BC,AC于点E,F,连接EF.
(1)求证:CD是⊙O的切线;
(2)求证:△CEF∽△CAD;
(3)若AB=10,AC=12,求tan∠CFE.
11.综合探究
如图,在Rt△ABC中,∠B=90°,在AC上取一点O,以点O为圆心,OC长为半径作圆,分别交AB于点D,交AC于点E,交BC于点F,连接CD,且D为的中点.
【问题初探】求证:AB为⊙O的切线;
【深入探究】连接DE,求证:△ACD∽△ADE;
【问题拓展】若,CD=8,求AE,AB的长.
12.如图1,AC为 ABCD的对角线,△ABC的外接圆⊙O交CD于点E,连接BE.
(1)求证:∠BAC=∠ABE;
(2)如图2,当AB=AC时,连接OA、OB,延长AO交BE于点G,求证△GOB∽△GBA;
(3)如图3,在(2)的条件下,记AC、BE的交点为点F,连接AE、OF.当时,求sin∠EAG的值.
13.如图1,⊙O经过平行四边形ABCD的A,C两点,且分别交AB,BC于E,F两点,其中EF=5,AC=12.
(1)求的值;
(2)如图2,若tan∠BAC tan∠ACB=1.
①求证:平行四边形ABCD为矩形;
②求⊙O的半径.
、
1.【解答】(1)证明:点D,E在以AC为直径的⊙O上,EH⊥AC,垂足为H,如图1,连接ED,
∴∠EAH+∠AEH=90°,∠AEC=90°,
∴∠EAH+∠ACE=90°,
∴∠ACE=∠AEH,
∴∠ADE=∠AEH,
又∵∠EAF=∠DAE,
∴△EAF∽△DAE,
∴,
∴AE2=AF AD;
(2)解:点D,E在以AC为直径的⊙O上,∠ADC的平分线交⊙O于点B,如图2,连接OB,过点G作GK⊥AD,垂足为K,过点G作GM⊥CD,垂足为M,
∴∠ADC=90°,∠AOB=2∠ADB=90°,GK=GM,
在等腰直角△AOB中,AB=5,
∴,
∴,
∵,∠ABD=∠ACD,
∴,
∴,则,
∵,,
∴,
∴,即,
∴,
∴,
∴.
2.【解答】(1)证明:∵,
∴∠CDB=∠CBD,
∵∠CAE=∠DBC,∠CAB=∠CDB,
∴∠CAE=∠CAB,
∴AC平分∠EAB;
(2)解:①过C作CH⊥AB于H,
∵AC平分∠EAB,DE⊥CE,
∴CE=CH,
∵AC=AC,
∴Rt△AEC≌Rt△AHC(HL),
∴AE=AH,
设AE=AH=x,
∵AB=4,
∴BH=4﹣x,
∵AB为⊙O的直径,
∴∠ACB=ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴,
∴AD=BDAB=2,
∴DE=AD+AE=2x,
∵∠E=∠BHC=90°,∠CDE=∠ABC,CB=CD,
∴△DEC≌△BHC(AAS),
∴DE=BH,
∴2x=4﹣x,
∴x=2,
∴AE=2;
②如图,
∵AB为⊙O的直径,
∴∠ACB=ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
过A作AM⊥CD于M,过B作BN⊥CD于N,
∴△ACM,△BCN是等腰直角三角形,
∵AC=x,BC=y,
∴AM=CMx,CN=BNy,
∵∠AMD=∠ADB=∠BND=90°,
∴∠ADM+∠BDN=∠ADM+∠DAM=90°,
∴∠DAM=∠BDN,
∵AD=BD,
∴△ADM≌△DBN(AAS),
∴DN=AMx,
∴CD=CN+DNyx=y,
∴y=()x.
3.【解答】(1)证明:如图1,连接OB,
∵PB是⊙O的切线,
∴∠PBO=90°,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(SSS),
∴∠PAO=∠PBO=90°,
∴OA⊥PA,
又∵点A在⊙O上,
∴PA是⊙O的切线;
(2)证明:如图2,连接BA、BC,
∵PB是⊙O的切线,
∴∠DBC=∠DAB,
又∵∠D=∠D,
∴△DBC∽△DAB,
∴,
∴DB2=DC DA;
(3)解:在Rt△OBD中,sin∠ADP,设OB=3x,OD=5x,
∴BD=4x,
∵BD=4,
∴x=1,
∴OB=3x=3,OD=5x=5,
在Rt△PAD中,sin∠ADP,
∴PB=6,
在Rt△POB中,OP.
4.【解答】(1)证明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°,
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,即∠OBF=90°,
∴OB⊥FB,
∵AB是⊙O的弦,
∴点B在⊙O上,
∴BF是⊙O的切线;
(2)解:∵AC∥BF,
∴∠ACF=∠F
∵CD=24,OA⊥CD,
∴CECD=12,
∵tan∠F,
∴tan∠ACF,
即,
解得AE=9,
连接OC,如图1所示:
设圆的半径为r,则OE=r﹣9,
在Rt△OCE中,CE2+OE2=OC2,
即122+(r﹣9)2=r2,
解得:r=12.5;
(3)解:是定值;理由如下:
连接BD,如图2所示:
∵∠DBG=∠ACF,∠ACF=∠F,
∴∠DBG=∠F,
∵∠DGB=∠FGB,
∴△BDG∽△FBG,
∴,
即GB2=DG GF,
∴.
5.【解答】(1)证明:连接OE,则:OE=OB,
∴∠OEB=∠OBE,
∵,以O为圆心,OB为半径的圆与AC切于点E,
∴OE⊥AC,
∴∠OEA=90°=∠C,
∴OE∥BC,
∴∠CBE=∠OEB,
∴∠CBE=∠OBE,
∴BE平分∠ABC;
(2)解:连接DE,过点E作EF⊥BD,
∵BD为直径,
∴∠BED=90°,
∵OB=4,
∴BD=8,
∴,
∵∠BED=90°,EF⊥BD,
∴,即:,
∴,
∵BE平分∠ABC,∠C=90°,EF⊥BD,
∴;
(3)∵OE∥BC,
∴,
∴,
∵OE⊥AC,
∴∠AEO=90°,
∴.
6.【解答】(1)证明:如图1中,
∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图2所示:
∵OF⊥BC,
∴,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴,
∴CE2=EH EA;
(3)解:连接BE,如图3所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE,
∴AB=10,BE=AB sin∠BAE=106,
∴EA8,
∵,
∴BE=CE=6,
∵CE2=EH EA,
∴EH,
∴在Rt△BEH中,BH.
7.【解答】(1)证明:连接OE,
∵BE是∠ABC的平分线,
∴∠ABC=∠ABE,
∵∠AOE=2∠ABE,
∴∠AOE=∠ABC,
∴OE∥BC,
∵AB是⊙O直径,
∴∠ACB=90°,
∴OE⊥AC,
∵EF∥AC,
∴OE⊥EF,
∵OE是半径,
∴EF是⊙O的切线;
(2)解:∵EF∥AC,
∴∠FEA=∠EAC,
∵∠EAC=∠EBC,
又∵∠ABE=∠CBE,
∴∠FEA=∠ABE,
又∵∠F=∠F,
∴△EFA∽△BFE,
∴,
∴EF2=AF BF
∵AF=1,EF=2,
∴FB=4,则AB=3,
∴OE=OA=1.5,则OF=2.5,
∵OE⊥EF,
∴;
(3)解:∵△EFA∽△BFE,
∴,
设AE=k,BE=2k,
∵∠AEB=90°,
∴AE2+BE2=AB2,即k2+4k2=32,
∴,
∴,
∴,
∴,
∵EF∥AC,
∴∠CAB=∠F,
∴,
∴,
在Rt△CBD中,设DC=x,,
∴DC2+BC2=BD2,即,
∴,
∴BD.
8.【解答】(1)解:如图,
(2)证明:∵,
∴∠ADB=∠EAB,
又∵∠ABD=∠EBA,
∴△ABE∽△DBA;
(3)解:设BE=DE=a,则BD=2a,
∵△ABE∽△DBA,
∴,
即,
故ABa,
在Rt△ABE中,AEa,
∵∠BAE=∠CDE,∠AEB=∠DEC,
∴△ABE∽△DCE,
∴,
即,
故CD,CE,
∴AC=AE+ECa;
∵AD是⊙O的直径,
∴∠ACD=90°,
在Rt△ACD中,tan2.
9.【解答】(1)证明,连接OC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OCA+∠OCB=90°.
∵OA=OC,
∴∠A=∠OCA,
∴∠A+∠OCB=90°
∵∠DCB=∠CAB,
∴∠OCB+∠DCB=90°,
∴∠OCD=90°,
∴OC⊥CD,
∵OC为⊙O的半径,
∴DC为⊙O的切线;
(2)证明:∵点E为的中点,
∴∠ACF=∠BCE.
∵∠A=∠E,
∴△ACF∽△ECB;
(3)解:∵∠A=∠E,
∴tanA=tan∠CEB,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴tanA,
设BC=a,则AC=2a,
∴ABa.
∴OC=OBABa.
∵∠D=∠D,∠DCB=∠CAB,
∴△DCB∽△DAC,
∴,
∵CD=4,
∴BD=2,
∴OD=OB+BDa+2.
∵OC⊥CD,
∴OC2+CD2=OD2,
∴,
∴a,
∴BC,AC.
由(2)知:△ACF∽△ECB,
∴,
∴CF CE=BC AC.
故答案为:.
10.【解答】(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠DCH=∠CHB,
∵CH⊥AB,
∴∠DCH=∠CHB=90°,即DC⊥CO,
又∵C是⊙O的半径的外端点,
∴CD是⊙O的切线.
(2)证明:连接FH,如图所示,
∵,
∴∠CEF=∠CHF,
∵CH为⊙O直径,
∴∠CFH=90°,∠CHF+∠FCH=90°,
∵CH⊥AB,
则∠CHA=90°,
∴∠CAH+∠FCH=90°,
∴∠CAH=∠CHF=∠CEF,
又∵AB∥CD,BC∥AD,
∴∠DCA=∠CAH,∠CAD=∠ACB,
∴∠DCA=∠CEF,∠CAD=∠FCE,
∴△CEF∽△CAD.
(3)解:连接BD交AC于点G,如图,
∵四边形ABCD是菱形,
∴AC⊥BD,,,AB=BC=10,
∴,
∴DB=2BG=16,
∴菱形ABCD的面积,
∴,
∴,
在Rt△CHB中,,
∵第(2)问已证∠CAH=∠CHF=∠CEF,
又∵∠FCE=∠BCA,
∴△CFE∽△CBA,
∴∠CFE=∠CBA,
∴.
11.【解答】【问题初探】证明:连接OD,如图,
∵D为的中点,
∴,
∴∠1=∠2.
∵OC=OD,
∴∠1=∠3.
∴∠2=∠3.
∴OD∥CB.
∴∠ADO=∠ABC=90°.
∴OD⊥AB.
∵OD为⊙O的半径,
∴AB为⊙O的切线.
【深入探究】证明:连接DE,如图,
∵CE 为⊙O的直径,
∴∠CDE=90°.
∴∠3+∠5=90°.
由(1)得:∠ADO=90°,
∴∠4+∠5=90°.
∴∠3=∠4.
∵∠1=∠3,
∴∠4=∠1.
又∵∠A=∠A,
∴△ACD∽△ADE.
【问题拓展】解:在Rt△CDE中,
∵.
∴CE=10.
∴OC=OE=5.
∴.
由(2)得△ACD∽△ADE,
∴.
设AE=3x,则AD=4x,AO=AE+OE=3x+5,
在Rt△AOD中,
∵AD2+OD2=AO2,
即:(4x)2+52=(3x+5)2,
解得:x=0(不合题意,舍去)或.
∴,
.
又∵∠1=∠2,
∴,
即:,
∴.
∴.
∴AE的长为,AB的长为.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠BEC,
∵弧BC=弧BC,
∴∠BAC=∠BEC,
∴∠BAC=∠ABE;
(2)证明:∵AB=AC,AO经过圆心,
∴∠BAG=∠CAG,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠BAC=∠ABE,
∴∠OAB=∠OBA=∠OBG,
又∠BGO=∠AGB,
∴△GOB∽△GBA;
(3)解:延长AO交BC于点H,
∵∠ABE=∠ACE=∠BEC,
∴EF=FC,
∵,
设EF=CF=7a,
则FG=9a,GE=16a,
∴BG=CG12a,
∵,
∴,
∵∠GCF=∠ECF,即CF是∠ECG的平分线,
∴点F到∠ECG两边的距离相等,
∴,
∴,
∵AB∥CD,
∴△CEF∽△ABF,
∴,
即,
∴AB=28a,
由(2)可知:OB是∠ABG的平分线,同理,
即,
∴,
设⊙O的半径为R,
∵BG2=GO GA,
∴(12a)2,
解得:,
即,
设OH=x,
在Rt△ABH和Rt△OBH中,(28a)2﹣(R+x)2=R2﹣x2,
整理得:,
即,
∵∠CAE=∠CBE,∠CAG=∠OBG,
∴∠EAG=∠OBH,
∴.
13.【解答】(1)解:∵四边形AEFC内接于⊙O,
∴∠EFC+∠EAC=180°,
∵∠EFC+∠EFB=180°,
∴∠EFB=∠EAC,
∵∠B=∠B,
∴△BEF∽△BCA,
∴,
∵AC=12,EF=5,
∴,
∵S四边形AEFC=S△BCA﹣S△BEF,
∴,
∵,
∴.
(2)①证明:如图,过点B作BM⊥AC于点M,
则,,
∵tan∠BAC tan∠ACB=1,
∴,
∴,
∵∠BMA=∠CMB=90°,
∴△BMA∽△CMB,
∴∠ABM=∠BCM,
∵∠BCM+∠CBM=90°,
∴∠CBM+∠ABM=90°,
∴∠ABC=90°,
∵四边形ABCD为平行四边形,
∴四边形ABCD为矩形.
②解:如图,连接CO并延长交⊙O于点P,连接AP,AF,
∵四边形AFCP内接于⊙O,
∴∠AFC+∠APC=180°,
∵∠AFC+∠AFB=180°,
∴∠APC=∠AFB,
∵CP为⊙O直径,∠B=90°,
∴∠CAP=∠ABF=90°,
∴△CAP∽△ABF,
∴∠EAF=∠ACP,
连接EO,FO和AO,
∵,,
∴∠EOF=2∠EAF,∠AOP=2∠ACP,
∴∠EOF=∠AOP,
∴AP=EF=5,
∵∠CAP=90°,
∴,
∴,
∴⊙O的半径为.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题
1.如图,点D,E在以AC为直径的⊙O上,∠ADC的平分线交⊙O于点B,连接BA,EC,EA,过点E作EH⊥AC,垂足为H,交AD于点F.
(1)求证:AE2=AF AD;
(2)若,AB=5,求S△BOG.
2.如图,△ABC内接于⊙O,AB为⊙O的直径,,连接AD、BD.CE⊥DA,交DA延长线于点E.
(1)证明:AC平分∠EAB;
(2)若CD平分∠ACB,
①当AB=4时,求AE的长;
②设AC=x,BC=y,直接写出y与x的函数关系式.
3.如图,PB是⊙O的切线,切点为B,点A在⊙O上,且PA=PB.连接AO并延长交⊙O于点C,交直线PB于点D,连接OP.
(1)证明:PA是⊙O的切线;
(2)证明:DB2=DC DA;
(3)若BD=4,sin∠ADP,求线段OP的长.
4.如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F,CD=24,求⊙O的半径;
(3)请问的值为定值吗?若是,请写出计算过程,若不是,请说明理由.
5.如图,在△ABC中,∠C=90°,O为边AB上的一点,以O为圆心,OB为半径的圆与AC切于点E,与AB交于另一点D.
(1)求证:BE平分∠ABC;
(2)若BO=4,BE=6,求CE的长;
(3)在(2)的条件下,直接写出cosA的值.
6.已知,如图,线段AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH EA;
(3)若⊙O的半径为5,sinA,求BH的长.
7.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.AF=1,EF=2,
(1)求证:EF是⊙O切线;
(2)求sin∠F;
(3)求BD的值.
8.如图,△ADP是直角三角形,∠PAD=90°,以AD为直径作⊙O,与PD相交于点B,连接AB.
(1)尺规作图:在劣弧BD上取点C,使得弧AB=弧BC,连接AC,交BD于点E;
(2)在(1)的条件下,求证:△ABE∽△DBA;
(3)在(2)的条件下,连接CD,若E为BD的中点,求tan∠ADC的值.
9.如图,AB是⊙O的直径,C为⊙O上一点,连接AC,BC,延长AB至点D,使得∠DCB=∠CAB,点E为的中点,连接CE交AB于点F,连接BE.
(1)求证:DC为⊙O的切线;
(2)求证:△ACF∽△ECB;
(3)若,则直接写出CF CE= .
10.如图,在菱形ABCD中,CH⊥AB于H,以CH为直径的⊙O分别交BC,AC于点E,F,连接EF.
(1)求证:CD是⊙O的切线;
(2)求证:△CEF∽△CAD;
(3)若AB=10,AC=12,求tan∠CFE.
11.综合探究
如图,在Rt△ABC中,∠B=90°,在AC上取一点O,以点O为圆心,OC长为半径作圆,分别交AB于点D,交AC于点E,交BC于点F,连接CD,且D为的中点.
【问题初探】求证:AB为⊙O的切线;
【深入探究】连接DE,求证:△ACD∽△ADE;
【问题拓展】若,CD=8,求AE,AB的长.
12.如图1,AC为 ABCD的对角线,△ABC的外接圆⊙O交CD于点E,连接BE.
(1)求证:∠BAC=∠ABE;
(2)如图2,当AB=AC时,连接OA、OB,延长AO交BE于点G,求证△GOB∽△GBA;
(3)如图3,在(2)的条件下,记AC、BE的交点为点F,连接AE、OF.当时,求sin∠EAG的值.
13.如图1,⊙O经过平行四边形ABCD的A,C两点,且分别交AB,BC于E,F两点,其中EF=5,AC=12.
(1)求的值;
(2)如图2,若tan∠BAC tan∠ACB=1.
①求证:平行四边形ABCD为矩形;
②求⊙O的半径.
、
1.【解答】(1)证明:点D,E在以AC为直径的⊙O上,EH⊥AC,垂足为H,如图1,连接ED,
∴∠EAH+∠AEH=90°,∠AEC=90°,
∴∠EAH+∠ACE=90°,
∴∠ACE=∠AEH,
∴∠ADE=∠AEH,
又∵∠EAF=∠DAE,
∴△EAF∽△DAE,
∴,
∴AE2=AF AD;
(2)解:点D,E在以AC为直径的⊙O上,∠ADC的平分线交⊙O于点B,如图2,连接OB,过点G作GK⊥AD,垂足为K,过点G作GM⊥CD,垂足为M,
∴∠ADC=90°,∠AOB=2∠ADB=90°,GK=GM,
在等腰直角△AOB中,AB=5,
∴,
∴,
∵,∠ABD=∠ACD,
∴,
∴,则,
∵,,
∴,
∴,即,
∴,
∴,
∴.
2.【解答】(1)证明:∵,
∴∠CDB=∠CBD,
∵∠CAE=∠DBC,∠CAB=∠CDB,
∴∠CAE=∠CAB,
∴AC平分∠EAB;
(2)解:①过C作CH⊥AB于H,
∵AC平分∠EAB,DE⊥CE,
∴CE=CH,
∵AC=AC,
∴Rt△AEC≌Rt△AHC(HL),
∴AE=AH,
设AE=AH=x,
∵AB=4,
∴BH=4﹣x,
∵AB为⊙O的直径,
∴∠ACB=ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴,
∴AD=BDAB=2,
∴DE=AD+AE=2x,
∵∠E=∠BHC=90°,∠CDE=∠ABC,CB=CD,
∴△DEC≌△BHC(AAS),
∴DE=BH,
∴2x=4﹣x,
∴x=2,
∴AE=2;
②如图,
∵AB为⊙O的直径,
∴∠ACB=ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
过A作AM⊥CD于M,过B作BN⊥CD于N,
∴△ACM,△BCN是等腰直角三角形,
∵AC=x,BC=y,
∴AM=CMx,CN=BNy,
∵∠AMD=∠ADB=∠BND=90°,
∴∠ADM+∠BDN=∠ADM+∠DAM=90°,
∴∠DAM=∠BDN,
∵AD=BD,
∴△ADM≌△DBN(AAS),
∴DN=AMx,
∴CD=CN+DNyx=y,
∴y=()x.
3.【解答】(1)证明:如图1,连接OB,
∵PB是⊙O的切线,
∴∠PBO=90°,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(SSS),
∴∠PAO=∠PBO=90°,
∴OA⊥PA,
又∵点A在⊙O上,
∴PA是⊙O的切线;
(2)证明:如图2,连接BA、BC,
∵PB是⊙O的切线,
∴∠DBC=∠DAB,
又∵∠D=∠D,
∴△DBC∽△DAB,
∴,
∴DB2=DC DA;
(3)解:在Rt△OBD中,sin∠ADP,设OB=3x,OD=5x,
∴BD=4x,
∵BD=4,
∴x=1,
∴OB=3x=3,OD=5x=5,
在Rt△PAD中,sin∠ADP,
∴PB=6,
在Rt△POB中,OP.
4.【解答】(1)证明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°,
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,即∠OBF=90°,
∴OB⊥FB,
∵AB是⊙O的弦,
∴点B在⊙O上,
∴BF是⊙O的切线;
(2)解:∵AC∥BF,
∴∠ACF=∠F
∵CD=24,OA⊥CD,
∴CECD=12,
∵tan∠F,
∴tan∠ACF,
即,
解得AE=9,
连接OC,如图1所示:
设圆的半径为r,则OE=r﹣9,
在Rt△OCE中,CE2+OE2=OC2,
即122+(r﹣9)2=r2,
解得:r=12.5;
(3)解:是定值;理由如下:
连接BD,如图2所示:
∵∠DBG=∠ACF,∠ACF=∠F,
∴∠DBG=∠F,
∵∠DGB=∠FGB,
∴△BDG∽△FBG,
∴,
即GB2=DG GF,
∴.
5.【解答】(1)证明:连接OE,则:OE=OB,
∴∠OEB=∠OBE,
∵,以O为圆心,OB为半径的圆与AC切于点E,
∴OE⊥AC,
∴∠OEA=90°=∠C,
∴OE∥BC,
∴∠CBE=∠OEB,
∴∠CBE=∠OBE,
∴BE平分∠ABC;
(2)解:连接DE,过点E作EF⊥BD,
∵BD为直径,
∴∠BED=90°,
∵OB=4,
∴BD=8,
∴,
∵∠BED=90°,EF⊥BD,
∴,即:,
∴,
∵BE平分∠ABC,∠C=90°,EF⊥BD,
∴;
(3)∵OE∥BC,
∴,
∴,
∵OE⊥AC,
∴∠AEO=90°,
∴.
6.【解答】(1)证明:如图1中,
∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
(2)证明:连接AC,如图2所示:
∵OF⊥BC,
∴,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴,
∴CE2=EH EA;
(3)解:连接BE,如图3所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE,
∴AB=10,BE=AB sin∠BAE=106,
∴EA8,
∵,
∴BE=CE=6,
∵CE2=EH EA,
∴EH,
∴在Rt△BEH中,BH.
7.【解答】(1)证明:连接OE,
∵BE是∠ABC的平分线,
∴∠ABC=∠ABE,
∵∠AOE=2∠ABE,
∴∠AOE=∠ABC,
∴OE∥BC,
∵AB是⊙O直径,
∴∠ACB=90°,
∴OE⊥AC,
∵EF∥AC,
∴OE⊥EF,
∵OE是半径,
∴EF是⊙O的切线;
(2)解:∵EF∥AC,
∴∠FEA=∠EAC,
∵∠EAC=∠EBC,
又∵∠ABE=∠CBE,
∴∠FEA=∠ABE,
又∵∠F=∠F,
∴△EFA∽△BFE,
∴,
∴EF2=AF BF
∵AF=1,EF=2,
∴FB=4,则AB=3,
∴OE=OA=1.5,则OF=2.5,
∵OE⊥EF,
∴;
(3)解:∵△EFA∽△BFE,
∴,
设AE=k,BE=2k,
∵∠AEB=90°,
∴AE2+BE2=AB2,即k2+4k2=32,
∴,
∴,
∴,
∴,
∵EF∥AC,
∴∠CAB=∠F,
∴,
∴,
在Rt△CBD中,设DC=x,,
∴DC2+BC2=BD2,即,
∴,
∴BD.
8.【解答】(1)解:如图,
(2)证明:∵,
∴∠ADB=∠EAB,
又∵∠ABD=∠EBA,
∴△ABE∽△DBA;
(3)解:设BE=DE=a,则BD=2a,
∵△ABE∽△DBA,
∴,
即,
故ABa,
在Rt△ABE中,AEa,
∵∠BAE=∠CDE,∠AEB=∠DEC,
∴△ABE∽△DCE,
∴,
即,
故CD,CE,
∴AC=AE+ECa;
∵AD是⊙O的直径,
∴∠ACD=90°,
在Rt△ACD中,tan2.
9.【解答】(1)证明,连接OC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OCA+∠OCB=90°.
∵OA=OC,
∴∠A=∠OCA,
∴∠A+∠OCB=90°
∵∠DCB=∠CAB,
∴∠OCB+∠DCB=90°,
∴∠OCD=90°,
∴OC⊥CD,
∵OC为⊙O的半径,
∴DC为⊙O的切线;
(2)证明:∵点E为的中点,
∴∠ACF=∠BCE.
∵∠A=∠E,
∴△ACF∽△ECB;
(3)解:∵∠A=∠E,
∴tanA=tan∠CEB,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴tanA,
设BC=a,则AC=2a,
∴ABa.
∴OC=OBABa.
∵∠D=∠D,∠DCB=∠CAB,
∴△DCB∽△DAC,
∴,
∵CD=4,
∴BD=2,
∴OD=OB+BDa+2.
∵OC⊥CD,
∴OC2+CD2=OD2,
∴,
∴a,
∴BC,AC.
由(2)知:△ACF∽△ECB,
∴,
∴CF CE=BC AC.
故答案为:.
10.【解答】(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠DCH=∠CHB,
∵CH⊥AB,
∴∠DCH=∠CHB=90°,即DC⊥CO,
又∵C是⊙O的半径的外端点,
∴CD是⊙O的切线.
(2)证明:连接FH,如图所示,
∵,
∴∠CEF=∠CHF,
∵CH为⊙O直径,
∴∠CFH=90°,∠CHF+∠FCH=90°,
∵CH⊥AB,
则∠CHA=90°,
∴∠CAH+∠FCH=90°,
∴∠CAH=∠CHF=∠CEF,
又∵AB∥CD,BC∥AD,
∴∠DCA=∠CAH,∠CAD=∠ACB,
∴∠DCA=∠CEF,∠CAD=∠FCE,
∴△CEF∽△CAD.
(3)解:连接BD交AC于点G,如图,
∵四边形ABCD是菱形,
∴AC⊥BD,,,AB=BC=10,
∴,
∴DB=2BG=16,
∴菱形ABCD的面积,
∴,
∴,
在Rt△CHB中,,
∵第(2)问已证∠CAH=∠CHF=∠CEF,
又∵∠FCE=∠BCA,
∴△CFE∽△CBA,
∴∠CFE=∠CBA,
∴.
11.【解答】【问题初探】证明:连接OD,如图,
∵D为的中点,
∴,
∴∠1=∠2.
∵OC=OD,
∴∠1=∠3.
∴∠2=∠3.
∴OD∥CB.
∴∠ADO=∠ABC=90°.
∴OD⊥AB.
∵OD为⊙O的半径,
∴AB为⊙O的切线.
【深入探究】证明:连接DE,如图,
∵CE 为⊙O的直径,
∴∠CDE=90°.
∴∠3+∠5=90°.
由(1)得:∠ADO=90°,
∴∠4+∠5=90°.
∴∠3=∠4.
∵∠1=∠3,
∴∠4=∠1.
又∵∠A=∠A,
∴△ACD∽△ADE.
【问题拓展】解:在Rt△CDE中,
∵.
∴CE=10.
∴OC=OE=5.
∴.
由(2)得△ACD∽△ADE,
∴.
设AE=3x,则AD=4x,AO=AE+OE=3x+5,
在Rt△AOD中,
∵AD2+OD2=AO2,
即:(4x)2+52=(3x+5)2,
解得:x=0(不合题意,舍去)或.
∴,
.
又∵∠1=∠2,
∴,
即:,
∴.
∴.
∴AE的长为,AB的长为.
12.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠BEC,
∵弧BC=弧BC,
∴∠BAC=∠BEC,
∴∠BAC=∠ABE;
(2)证明:∵AB=AC,AO经过圆心,
∴∠BAG=∠CAG,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠BAC=∠ABE,
∴∠OAB=∠OBA=∠OBG,
又∠BGO=∠AGB,
∴△GOB∽△GBA;
(3)解:延长AO交BC于点H,
∵∠ABE=∠ACE=∠BEC,
∴EF=FC,
∵,
设EF=CF=7a,
则FG=9a,GE=16a,
∴BG=CG12a,
∵,
∴,
∵∠GCF=∠ECF,即CF是∠ECG的平分线,
∴点F到∠ECG两边的距离相等,
∴,
∴,
∵AB∥CD,
∴△CEF∽△ABF,
∴,
即,
∴AB=28a,
由(2)可知:OB是∠ABG的平分线,同理,
即,
∴,
设⊙O的半径为R,
∵BG2=GO GA,
∴(12a)2,
解得:,
即,
设OH=x,
在Rt△ABH和Rt△OBH中,(28a)2﹣(R+x)2=R2﹣x2,
整理得:,
即,
∵∠CAE=∠CBE,∠CAG=∠OBG,
∴∠EAG=∠OBH,
∴.
13.【解答】(1)解:∵四边形AEFC内接于⊙O,
∴∠EFC+∠EAC=180°,
∵∠EFC+∠EFB=180°,
∴∠EFB=∠EAC,
∵∠B=∠B,
∴△BEF∽△BCA,
∴,
∵AC=12,EF=5,
∴,
∵S四边形AEFC=S△BCA﹣S△BEF,
∴,
∵,
∴.
(2)①证明:如图,过点B作BM⊥AC于点M,
则,,
∵tan∠BAC tan∠ACB=1,
∴,
∴,
∵∠BMA=∠CMB=90°,
∴△BMA∽△CMB,
∴∠ABM=∠BCM,
∵∠BCM+∠CBM=90°,
∴∠CBM+∠ABM=90°,
∴∠ABC=90°,
∵四边形ABCD为平行四边形,
∴四边形ABCD为矩形.
②解:如图,连接CO并延长交⊙O于点P,连接AP,AF,
∵四边形AFCP内接于⊙O,
∴∠AFC+∠APC=180°,
∵∠AFC+∠AFB=180°,
∴∠APC=∠AFB,
∵CP为⊙O直径,∠B=90°,
∴∠CAP=∠ABF=90°,
∴△CAP∽△ABF,
∴∠EAF=∠ACP,
连接EO,FO和AO,
∵,,
∴∠EOF=2∠EAF,∠AOP=2∠ACP,
∴∠EOF=∠AOP,
∴AP=EF=5,
∵∠CAP=90°,
∴,
∴,
∴⊙O的半径为.
21世纪教育网(www.21cnjy.com)
同课章节目录
