2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 05:53:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题练习
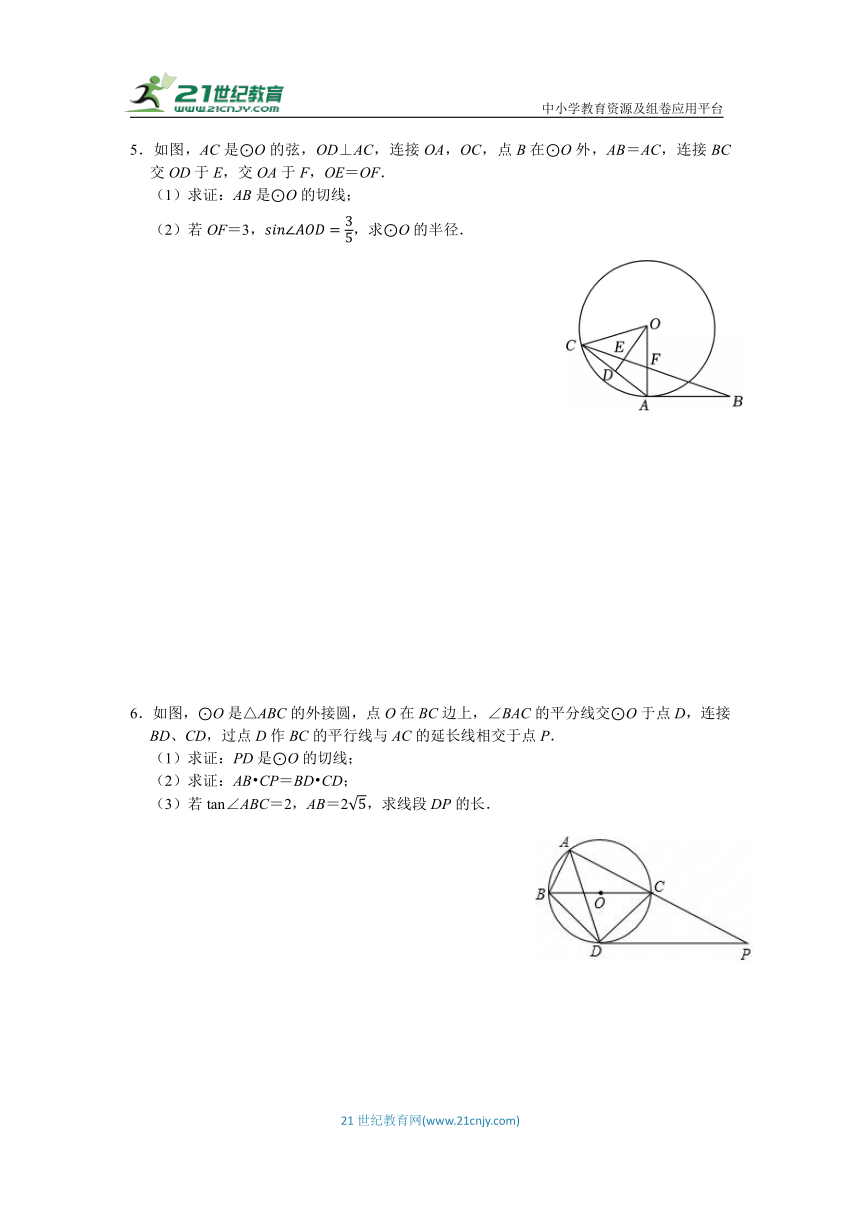
1.如图,AB是⊙O的直径,点C是⊙O上的一点,点D为弧AB的中点,过点D作AB的平行线交CB的延长线于点E.
(1)如图1,求证:△ADC∽△DEC;
(2)若⊙O的半径为3,求CA CE的最大值;
(3)如图2,连接AE,设tan∠ABC=x,tan∠AEC=y,①求y关于x的函数解析式;②若,求y的值.
2.如图,⊙O上有A,B,C三点,AC是直径,点D是的中点,连接CD交AB于点E,点F在AB延长线上且FC=FE.
(1)证明:∠BCE=∠ACE;
(2)求证:CF是⊙O的切线;
(3)若,BE=2,求DE EC的值.
3.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)求证:CD2=CA CB;
(3)若CD=4,CB=8,求tan∠CDA的值.
4.如图,AB是半圆O的直径,AB=10.C是弧AB上一点,连接AC,BC,∠ACB的平分线交AB于点P,过点P分别作PE⊥AC,PF⊥BC,垂足分别为E、F.
(1)求证:四边形CEPF是正方形;
(2)当sinA时,求CP的长;
(3)设AP的长为x,图中阴影部分的面积为y,求y与x之间的函数关系式,并写出y的最大值.
5.如图,AC是⊙O的弦,OD⊥AC,连接OA,OC,点B在⊙O外,AB=AC,连接BC交OD于E,交OA于F,OE=OF.
(1)求证:AB是⊙O的切线;
(2)若OF=3,,求⊙O的半径.
6.如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:AB CP=BD CD;
(3)若tan∠ABC=2,AB=2,求线段DP的长.
7.如图1,在⊙O中,直径AB=10,D是AB上的动点,过点D作EF⊥AB交⊙O于点E,F连接BE,取BE的中点H,连接FH交AB于点M,并延长FH交⊙O于点C,连接CB.
(1)当点D与圆心O重合时,如图2所示,求FM FC的值.
(2)在点D的运动过程中,的值是否为定值?若是,请求出定值;若不是,请说明理由.
(3)连接OH,DH,当△ODH是等腰三角形时,求tanC的值.
8.已知在Rt△ABC中,∠ACB=90°,BC=6,AC=8,以边AC为直径作⊙O,与AB边交于点D,点M为边BC的中点,连接DM.
(1)求证:DM是⊙O的切线;
(2)点P为直线BC上任意一动点,连接AP交⊙O于点Q,连接CQ.
①当tan∠BAP时,求BP的长;
②求的最大值.
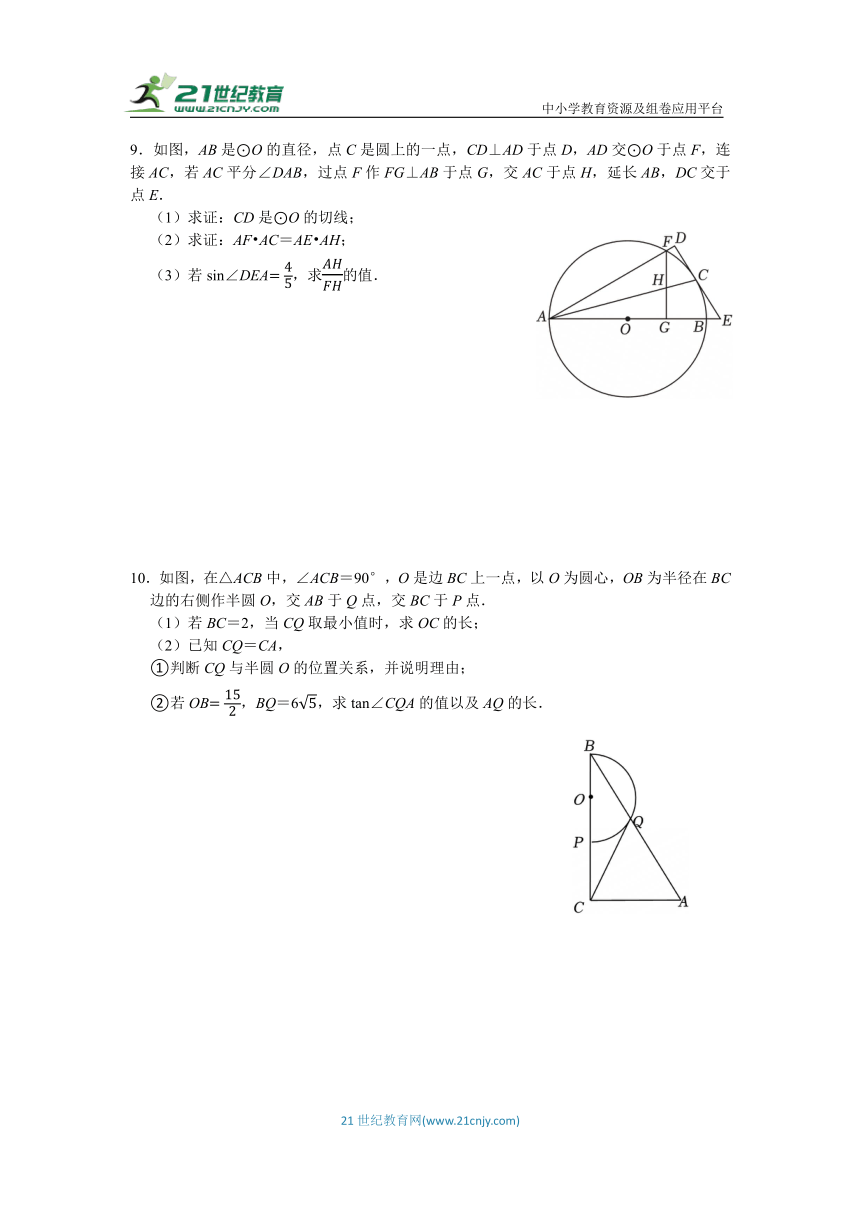
9.如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G,交AC于点H,延长AB,DC交于点E.
(1)求证:CD是⊙O的切线;
(2)求证:AF AC=AE AH;
(3)若sin∠DEA,求的值.
10.如图,在△ACB中,∠ACB=90°,O是边BC上一点,以O为圆心,OB为半径在BC边的右侧作半圆O,交AB于Q点,交BC于P点.
(1)若BC=2,当CQ取最小值时,求OC的长;
(2)已知CQ=CA,
①判断CQ与半圆O的位置关系,并说明理由;
②若OB,BQ=6,求tan∠CQA的值以及AQ的长.
11.如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F
(1)求证:ED是⊙O的切线;
(2)求证:△CFP∽△CPD;
(3)如果CF=1,CP=2,sinA,求O到DC的距离.
12.如图,已知△ABP中,C是BP边上的一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD于点F,延长CF交AB于点G,若AG AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求sin∠ACE的值.
13.如图,四边形ABDC内接于⊙O,AD是⊙O的直径,延长CD,AB交于点E,连接BC交AD于点M,过点B作BF⊥CE,垂足为点F,已知∠BDF=∠ACB.
(1)求证:BF为⊙O的切线;
(2)若OA=4,sin∠ACB,求BC的值;
(3)若CD=DF,则的值是多少?
14.如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相交于点M,连接DM,求证:DM=DC;
(3)若,求证:AM=CE.
15.如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H.
(1)求证:CD是⊙O的切线;
(2)求sin∠FHG的值;
(3)若GH=4,HB=2,求⊙O的直径.
16.如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H.
(1)求证:CD是⊙O的切线;
(2)延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;
(3)在(2)的条件下,求的值.
17.如图,四边形ABCD是⊙O的内接四边形,D是的中点,过点D作BC延长线的垂线,垂足为E,AB为⊙O的直径.
(1)求证:DE是⊙O的切线;
(2)求证:AD2=AB CE;
(3)若BC=6,tan∠A=2,求⊙O的半径.
18.如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC,AK,求BF的长.
19.如图,在Rt△ABC中,AF是⊙O的直径,BC交AF的延长线于点F.过点D的切线交BC于点B,连接OB交⊙O于点M,使∠DBO=∠CBO,BM=1.
(1)求证:BC是⊙O的切线;
(2)若CF=2,sinC,试求cos∠DBO的值.
(3)连接AD,分别延长AC,BD交于点N.当△ABC为等腰直角三角形时是否存在△CBN∽△DAN?若存在,请直接写出它们面积的相似比;若不存在,请你用反证法尝试证明.
参考答案
1.【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEC,
∵∠ADC=∠ABC,
∴∠ADC=∠DEC,
∵点D为弧AB的中点,
∴,
∴∠ACD=∠DCE,
∴△ADC∽△DEC;
(2)解:∵△ADC∽△DEC,
∴,
即CD2=CA CE,
又∵⊙O的半径为3,
∴CA CE=CD2≤62=36.
即CA CE的最大值为36;
(3)解:①∵△ADC∽△DEC,
∴,
∴y=tan∠AEC()2,
过点D作DF⊥CE,不妨设EF=a,
∵∠CED=∠CBA,∠DCE=45°,
∴CF=DF=ax,
∴CDax,
∴y=()2=()2;
②∵,
∴,
∴:8:3,
即x:y=8:3,
将yx代入y得,
x,
解得,x1=3,x2,
当x=3时,y,
当x时,y,
∴y或.
2.【解答】(1)证明:∵点D是的中点,
∴,
∴∠BCE=∠ACE;
(2)证明:∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠BEC+∠BCE=90°,
∵FC=FE,
∴∠FCE=∠FEC,
由(1)可知∠BCE=∠ACE,
∴∠FCE+∠ACE=90°,
∴∠OCF=90°,
∵OC是⊙O的半径,
∴CF是⊙O的切线;
(3)解:在Rt△FBC中,BE=2,sinF,
∴,
设BC=4x,CF=5x,
∵BC2+BF2=CF2,
∴(4x)2+(5x﹣2)2=(5x)2,
∴x=1或x(舍去),
∴BC=4,CF=5,BF=3,
∵∠CBF=∠ACF=90°,∠F=∠F,
∴△FBC∽△FCA,
∴,
∴,
∴CA,
∵sinF,
∴,
∴AF,
∴AE=AF﹣EF,
连接DA,
∵∠DAE=∠BCE,∠AED=∠CEB,
∴△AED∽△CEB,
∴,
∴AE BE=DE CE,
∴DE CE.
3.【解答】(1)证明:如图,连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
∴∠CDO=90°,
∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)证明:∵CD是⊙O的切线,
∴∠CDO=90°,
∴∠CDA+∠ADO=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DBA+∠DAB=90°,
又∵OA=OD,
∴∠DAB=∠ODA,
∴∠CDA=∠DBA,
又∵∠DCA=∠BCD,
∴△CAD∽△CDB,
∴,
∴CD2=CA CB;
(3)∵∠CDA=∠DBA,
在Rt△ABD中,tan∠CDA,
又∵,
∵CD=4,CB=8,
∴tan∠CDA.
4.【解答】(1)证明:∵∠ACB=90°,PE⊥AC,PF⊥BC,
∴四边形PECF是矩形,
∵CP平分∠ACB,PE⊥AC,PF⊥BC,
∴PE=PF,
∴四边形CEPF是正方形;
(2)解:∵sinA,AB=10,
∴,
∴BC=8,
∴AC6,
∴tanA,
设PE=CE=m,则AE=6﹣m,
∴tanA,
∴m,
∴PCPE;
(3)解:∵四边形CEPF是正方形,
∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,
∴将△APE绕点P顺时针旋转90°,得到△A′PF,PA′=PA,如图所示:
则A′、F、B三点共线,∠APE=∠A′PF,
∴∠A′PF+∠BPF=90°,即∠A′PB=90°,
∴S△PAE+S△PBF=S△PA′BPA′ PBx(10﹣x),
∴y与x之间的函数关系式为y5x,
∵y5x,
∴x=5时,y有最大值为.
5.【解答】(1)证明:∵OD⊥AC,
∴∠DCE+∠DEC=90°,
∵AC=AB,
∴∠ACB=∠B,
∵OE=OF,
∴∠OEF=∠OFE,
∵∠DEC=∠OEF,∠AFB=∠OFE,
∴∠DEC=∠AFB,
∴∠AFB+∠B=90°,
∴∠OAB=90°,
∵OA是⊙O的半径,
∴AB是⊙O的切线;
(2)解:∵OD⊥AC,
∴AD=CD,
Rt△ADF中,tanB,
在Rt△AOD中,
sin∠AOD,tan∠ACB,
设AD=3x,OA=5x,
∴OD4x,
∵OE=OF=3,
∴DE=4x﹣3,AF=5x﹣3,
∴AC=2AD=6x,
∴AB=6x,
∵∠ACB=∠B,
∴tan∠ACB=tanB,
∴,
∴,
解得x=1,
∴OA=5x=5,
∴⊙O的半径为5.
6.【解答】(1)证明:如图1,连接OD.
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴,
∴∠BOD=∠COD=90°,
∵BC∥PD,
∴∠ODP=∠BOD=90°,
∴OD⊥PD,
∴PD是⊙O的切线.
(2)证明:∵BC∥PD,
∴∠PDC=∠BCD.
∵∠BCD=∠BAD,
∴∠BAD=∠PDC,
∵∠ABD+∠ACD=180°,∠ACD+∠PCD=180°,
∴∠ABD=∠PCD,
∴△BAD∽△CDP,
∴,
∴AB CP=BD CD;
(3)解:∵BC是⊙O的直径,
∴∠BAC=90°,
∵tan∠ABC=2,,
∴2,
∴,
∴,
∴OD=5,
如图2,连接OD,过点C作CG⊥DP,垂足为G,则四边形ODGC为正方形,
∴DG=CG=OD=5,
∵BC∥PD,
∴∠CPG=∠ACB,
∴tan∠CPG=tan∠ACB,
∴,即,
解得,GP=10,
∴DP=DG+PG=5+10=15.
7.【解答】解:(1)连接CE,
∵AB=10,
∴OF=OE=5,
∵EF是直径,
∴∠ECF=90°,
∵∠MFO=∠EFC,∠MOF=∠ECF=90°,
∴△MOF∽△ECF,
∴,
∴FM CF=EF OF=50;
(2)是定值,理由如下:
过点H作HN⊥EF,垂足为点N,
∵EF⊥AB,
∴DE=DF,
设DE=DF=2x,
∵点H是BE中点,
∴,
∵HN⊥EF,EF⊥AB,
∴HN∥AB,
∴,
∴EN=DN,
∴DNDE=x,
∴FN=DF+DN=3x,
∵HN∥AB,
∴△FMD∽△FHN,
∴,
∴;
(3)若点D在点O的左侧,此时有OD=OH,连接OE,
∵点H是BE的中点,
∴OH⊥BE,
∵∠EDO=∠EHO,OD=OH,EO=EO,
∴Rt△DOE≌△HOE(HL),
∴DE=EH,
在Rt△BDE中,
∵点H是BE的中点,
∴DH=EH=BH,
∴DE=DH=EH,
∴△DHE是等边三角形,
∴∠BEF=60°,
∵,
∴∠C=∠BEF=60°,
∴tanC;
若点D在点O的右侧,此时有OD=DH,
∵点H是BE中点,
∴OH⊥BE,
∴∠OHB=90°,
∴∠HOB+∠OBH=90°,∠OHD+∠DHB=90°,
∵OD=DH,
∴∠HOB=∠OHD,
∴∠OBH=∠DHB,
∴DH=BD,
在Rt△BDE中,
∵点H是BE的中点,
∴DH=BH=EH,
∴DH=BD=BH,
∴△BDH是等边三角形,
∴∠DBE=60°,
∴∠BEF=30°,
∵,
∴∠C=∠BEF=30°,
∴tanC;
综上所述,当△ODH是等腰三角形时,tanC或.
8.【解答】(1)证明:如图,连接OD,CD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠BDC=180°﹣∠ADC=90°,
∵点M为边BC的中点,
∴MC=MD,
∴∠MDC=∠MCD,
∵OC=OD,
∴∠ODC=∠OCD,
∵∠ACB=90°,即∠MCD+∠OCD=90°,
∴∠MDC+ODC=∠MCD+∠OCD=90°,
即∠ODM=90°,
∴DM⊥OD,
∵OD是⊙O的半径,
∴DM是⊙O的切线;
(2)①当点P在线段BC上时,如图,过点P作PT⊥AB于点T,
在Rt△ABC中,AB10,
设PT=x,
∵tan∠BAP,
∴,
∴AT=3PT=3x,
∴BT=AB﹣AT=10﹣3x,
∵tan∠ABC,
∴,
解得:x,
∴PT,
∵sin∠ABC,即,
∴BP;
当点P在CB的延长线上时,如图,过点B作BK⊥AP于点K,
∵tan∠BAP,
∴,
设BK=a,则AK=3a,
在Rt△ABK中,AK2+BK2=AB2,
即(3a)2+a2=102,
解得:a1,a2(舍去),
∴AK=3,BK,
∵S△ABPAP BKBP AC,
∴,
设BP=m,则APm,
在Rt△ACP中,AC2+CP2=AP2,
即82+(m+6)2=(m)2,
解得:m1,m2(舍去),
∴BP;
综上所述,BP的长为或;
②设CP=n,则AP,
如图,∵AC是⊙O的直径,
∴CQ⊥AP,
∵CQ AP=AC CP,
∴CQ,
∴,
∵n>0,
∴(n﹣8)2≥0,
∴64+n2≥16n,
∴,
∴的最大值为.
9.【解答】(1)证明:连接OC,
∵AC平分∠DAB,
∴∠DAC=∠EAC,
∵∠OCA=∠EAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵CD⊥AD,
∴OC⊥AD,
∵OC是半径,
∴CD是⊙O的切线;
(2)证明:∵AC平分∠DAB,
∴∠DAC=∠EAC,
又∵CD⊥AD,FG⊥AB,
∴∠AGF=∠D=90°,
∴∠AFG+∠DAG=90°,∠E+∠DAE=90°,
∴∠AFG=∠DEA,
∴△AHF∽△ACE,
∴,
即AF AC=AE AH;
(3)过H作HM⊥AD,如图:
由(2)知∠AFG=∠DEA,
∴sin∠DEAsin∠AFG,
设AG=4x,AF=5x,则FG=3x,
∵AC平分∠DAB,
∴MH=GH,AG=AM=4x,
∴MF=x,
设GH=MH=a,
∴tan∠AFG,
∴,
∴ax,
∴FH=3xxx,
AH,
∴.
10.【解答】解:(1)当CQ取最小值时,CQ⊥AB,此时P点与C点重合,O是BC的中点,
∵BC=2,
∴OC=1;
(2)①CQ与半圆O相切,
理由如下:连接OQ,
∵OB=OQ,
∴∠B=∠OQB,
∵CQ=CA,
∴∠CQA=∠A,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠OQB+∠CQA=90°,
∴∠OQC=180°﹣(∠OQB+∠CQA)=90°,
∴OQ⊥QC,
又∵OQ是圆的半径,
∴CQ与半圆O相切;
②如图,连接PQ,过C作CD⊥AB于D,
由题意得,BP=2OB=15,BQ,
∵BP是直径,
∴∠BQP=90°,
∴PQ,
∵∠PQA+∠A+∠PCA+∠CPQ=360°,
∴∠A+∠CPQ=180°,
∵∠CPQ+∠BPQ=180°,
∴∠A=∠BPQ,
∵CQ=CA,
∴∠A=∠CQA,
∴tan∠CQA=tan∠BPQ,
∵CQ=CA,
∴QD=DA,
设QD=a,
∵tan∠CQA2,
∴CD=2a,
∵∠PQB=∠CDB=90°,
∴PQ∥CD,
∴∠BPQ=∠BCD,
∴tan∠BCD=tan∠BPQ=2,
∴BD=4a,
∴BQ=3a,
∴a,
∴AQ.
11.【解答】(1)证明:连接OD.
∵BC为直径,
∴△BDC为直角三角形.
在Rt△ADB中,E为AB中点,
∴BE=DE,
∴∠EBD=∠EDB.
又∵OB=OD,∴∠OBD=∠ODB,
∵∠OBD+∠ABD=90°,∴∠ODB+∠EDB=90°.
∴ED是⊙O的切线.
(2)证明:∵PF⊥BC,
∴∠FPC=90°﹣∠BCP(直角三角形的两个锐角互余).
∵∠PDC=90°﹣∠PDB(直径所对的圆周角是直角),∠PDB=∠BCP(同弧所对的圆周角相等),
∴∠FPC=∠PDC(等量代换).
又∵∠PCF是公共角,
∴△PCF∽△DCP.
(3)解:过点O作OM⊥CD于点M,
∵△PCF∽△DCP,
∴PC2=CF CD(相似三角形的对应边成比例).
∵CF=1,CP=2,
∴CD=4.
可知sin∠DBC=sinA=sin∠MOC,
∴,即,
∴直径BC=5,
∴,
∴MC=2,
∴MO,
∴O到DC的距离为.
12.【解答】(1)证明:连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠ADC=90°.
∵∠PAC=∠PBA,∠ADC=∠PBA,
∴∠PAC=∠ADC,
∴∠CAD+∠PAC=90°,
∴PA⊥OA,而AD是⊙O的直径,
∴PA是⊙O的切线;
(2)解:由(1)知,PA⊥AD,
∵CF⊥AD,
∴CF//PA,
∴∠GCA=∠PAC.
∵∠PAC=∠PBA,
∴∠GCA=∠PBA.
又∵∠CAG=∠BAC,
∴△CAG∽△BAC,
∴,
即AC2=AG AB.
∵AG AB=12,
∴;
(3)解:∵AF:FD=1:2,
设AF=x,FD=2x,则AD=AF+FD=3x.
在Rt△ACD 中,
∵CF⊥AD,
∴∠AFC=∠ACD=90°.
又∵∠CAF=∠DAC,
∴△CAF∽△DAC,
∴,
∴AC2=AF AD,
即3x2=12,
解得x=2,
∴AF=2,FD=4,AD=6.
在Rt△AFG 中,
∵AF=2,GF=1,
∴.
由(2)知,AG AB=12,
∴.
连接BD,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴.
∵∠ACE=∠ACB=∠ADB,
∴.
13.【解答】(1)证明:连接OB.
∵四边形ABDC内接于⊙O,
∴∠BDC+∠BAC=180°,
∵∠BDF+∠BDC=180°,
∴∠BAC=∠BDF,
∵∠BDF=∠ACB.
∴∠BAC=∠ACB,
∴AB=CB,
∵AC⊥CE,
∴∠ACE=90°,
∴∠E+∠EAC=90°,∠BCE+∠ACB=90°,
∴∠E=∠BCE,
∴EB=CB,
∴AB=BE,
∴OB是△ADE的中位线.
∴OB∥CE,
∵BF⊥CE,
∴BF⊥OB,
∴BF为⊙O的切线;
(2)解:∵AD是直径,
∴∠ABD=90°,
∵∠ADB=∠ACB,
∴sin∠ACB=sin∠ADB,
∵AD=2OA=8,
∴AB=6,
∴BC=AB=6;
(3)解:设CD=DF=a,
由(2)知BE=BC.
又∵BF⊥CE,
∴CF=EF=2a
∴DE=3a,
由(1)可知,OB是△ADE的中位线,
∴OB∥DE且OBDE,
∴△BOM∽△CDM.
∴,
∴.
14.【解答】证明:(1)如图所示,连接OD,
∵AB=AC,OB=OD,
∴∠C=∠B=∠ODB,
∵DE⊥AC,即∠DEC=90°,
∴∠C+∠CDE=90°,
∴∠ODB+∠CDE=90°,
∴∠ODE=90°,
∴OD⊥OE,
又∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)如图所示,连接OM,
∵OA=OM,
∴∠OAM=∠OMA,
∵OD⊥DE,AC⊥DE,
∴AC∥OD,
∴∠BOD=∠OAM=∠DOM=∠OMA,∠ODM=∠DMC,∠C=∠ODB,
∵OB=OD=OM,
∴△OBD≌△OMD(SAS),
∴∠ODB=∠ODM=∠DMC,
∴∠DMC=∠C,
∴DM=DC;
(3)∵AB是直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=CD,
在Rt△ABD中,,
∴可设,
∴,
∵∠CDE+∠C=90°=∠BAD+∠B,∠B=∠C,
∴∠CDE=∠BAD,
∴sin∠CDE=sin∠BAD,
在Rt△CDE中,,
∵DM=DC,DE⊥CM,
∴,
∴,
∴AM=CE.
15.【解答】(1)证明:连接OF.
∵OA=OF,
∴∠OAF=∠OFA,
∵,
∴∠CAF=∠FAB,
∴∠CAF=∠AFO,
∴OF∥AC,
∵AC⊥CD,
∴OF⊥CD,
∵OF是半径,
∴CD是⊙O的切线.
(2)解:∵AB是直径,
∴∠AFB=90°,
∵OF⊥CD,
∴∠OFD=∠AFB=90°,
∴∠AFO=∠DFB,
∵∠OAF=∠OFA,
∴∠DFB=∠OAF,
∵GD平分∠ADF,
∴∠ADG=∠FDG,
∵∠FGH=∠OAF+∠ADG,∠FHG=∠DFB+∠FDG,
∴∠FGH=∠FHG=45°,
∴sin∠FHG;
(3)解:过点H作HM⊥DF于点M,HN⊥AD于点N.
∵HD平分∠ADF,
∴HM=HN,
∵,
∵△FGH是等腰直角三角形,GH=4,
∴FH=FG=4,
∴2,
设DB=k,DF=2k,
∵∠FDB=∠ADF,∠DFB=∠DAF,
∴△DFB∽△DAF,
∴DF2=DB DA,
∴AD=4k,
∵GD平分∠ADF,
∴∠FDH=∠ADG,
∴△FDH∽△ADG,
∴,
∴AG=8,
∵∠AFB=90°,AF=12,FB=6,
∴AB6,
∴⊙O的直径为6.
解法二:由(2)可知sin∠FHG,
∴FH=FG=4,
∴FB=FH+HB=4+2=6,2,
∵DG是∠FDA的角平分线,
可证2,
∵△DAF∽△DFB,
∴,
∴AF=12,
∵∠AFB=90°,AF=12,FB=6,
∴AB6.
解法三:可以作GP⊥AF交AD于点P,再证△DFG≌△DGP,△AGP∽△AFB可以求出AF的长,用勾股定理求出直径AB的长.
16.【解答】(1)证明:如图1,连接OC,
∵OA=OC,
∴∠CAO=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠ACO,
∴AD∥OC,
∵CD⊥AD,
∴OC⊥CD,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)解:∵AE=4BE,OA=OB,
设BE=x,则AB=3x,
∴OC=OB=1.5x,
∵AD∥OC,
∴∠COE=∠DAB,
∴cos∠DAB=cos∠COE;
(3)解:由(2)知:OE=2.5x,OC=1.5x,
∴EC2x,
∵FG⊥AB,
∴∠AGF=90°,
∴∠AFG+∠FAG=90°,
∵∠COE+∠E=90°,∠COE=∠DAB,
∴∠E=∠AFH,
∵∠FAH=∠CAE,
∴△AHF∽△ACE,
∴.
17.【解答】(1)证明:连接OD,BD,如图,
∵DE⊥BE,
∴∠EDB+∠EBD=90°.
∵D是的中点,
∴∠EBD=∠ABD.
∵OD=OB,
∴∠ABD=∠ODB.
∴∠ODB=∠EBD.
∴∠ODB+∠EDB=90°.
即OD⊥DE.
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∵四边形ABCD为⊙O的内接四边形,
∴∠ECD=∠A.
∵DE⊥BE,
∴∠DEC=90°.
∴∠ADB=∠DEC.
∴△ABD∽△CDE.
∴.
∵D是的中点,
∴.
∴AD=CD
∴.
∴AD2=AB CE;
(3)解:∵∠ECD=∠A,tan∠A=2,
∴tan∠ECD.
∴DE=2CE.
∵△ABD∽△CDE,
∴∠EDC=∠ABD=∠EBD.
∵∠E=∠E,
∴△EDC∽△EBD.
∴.
∴ED2=EC EB.
∵BC=6,
∴4EC2=EC(EC+6).
∵EC≠0
∴EC=2,DE=4.
∴BD2=DE2+BE2=64+16=80.
∵CD2=DE2+CE2=16+4=20,
∴AD2=20.
∵AD2=AB CE,
∴AB10.
∴OA=5.
∴⊙O的半径为5.
18.【解答】解:(1)如图,连接OG.
∵EG=EK,
∴∠KGE=∠GKE=∠AKH,
又OA=OG,
∴∠OGA=∠OAG,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
∴∠KGE+∠OGA=90°,
∴EF是⊙O的切线.
(2)①∵AC∥EF,
∴∠E=∠C,
又∠C=∠AGD,
∴∠E=∠AGD,
又∠DKG=∠GKE,
∴△KGD∽△KEG;
②连接OG,
∵,AK,
设cosC,
∴CH=4k,AC=5k,则AH=3k,
∵KE=GE,AC∥EF,
∴CK=AC=5k,
∴HK=CK﹣CH=k.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即,
解得k=1,
∴CH=4,AC=5,则AH=3,
设⊙O半径为R,在Rt△OCH中,OC=R,OH=R﹣3k,CH=4k,
由勾股定理得:OH2+CH2=OC2,即(R﹣3)2+42=R2,
∴,
在Rt△OGF中,,
∴,
∴.
19.【解答】(1)证明:方法一:
连接OD,过点O作OE⊥BC于点E,如图,
∵BD为⊙O的切线,
∴OD⊥BD,
∴∠ODB=90°.
∵OE⊥BC,
∴∠OEB=90°.
∴∠ODB=∠OEB.
在△ODB和△OEB中,
,
∴△ODB≌△OEB(AAS),
∴OD=OE.
即OE为⊙O的半径,
∴BC是⊙O的切线;
方法二:
连接OD,过点O作OE⊥BC于点E,如图,
∵BD为⊙O的切线,
∴OD⊥BD,
∵∠DBO=∠CBO,OE⊥BC,
∴OD=OE.
即OE为⊙O的半径,
∴BC是⊙O的切线;
(2)解:在Rt△OEC中,
∴sinC,
∵sinC,
∴,
设OE=2k,则OC=5k,
∵OF=OE=2k,
∴CF=OC﹣OF=3k=2,
∴k.
∴OE=2k,
∴OM=OE.
∴OB=OM+MB=1.
∴BE.
∴cos∠EBO.
∵∠DBO=∠CBO,
∴cos∠DBO=cos∠CBO;
(3)解:当△ABC为等腰直角三角形时,不存在△CBN∽△DAN,理由:
用反证法:
假设△CBN∽△DAN,如图,
∵△ABC为等腰直角三角形,
∴∠C=∠BAC=45°,
∵CBN∽△DAN,
∴∠ADN=∠C=45°.
∵BD为⊙O的切线,
∴OD⊥BD,
∴∠ODN=90°,
∴∠ODA=90°﹣∠ADN=45°.
∵OD=OA,
∴∠OAD=∠ODA=45°,
∴∠AOD=90°,
∴OD⊥AC,
∵OD⊥BN,
∴AC∥BD,
这与BD与AC相交于点N矛盾,
∴假设不成立,
∴当△ABC为等腰直角三角形时,不存在△CBN∽△DAN.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺圆中相似三角形和锐角三角函数综合问题练习
1.如图,AB是⊙O的直径,点C是⊙O上的一点,点D为弧AB的中点,过点D作AB的平行线交CB的延长线于点E.
(1)如图1,求证:△ADC∽△DEC;
(2)若⊙O的半径为3,求CA CE的最大值;
(3)如图2,连接AE,设tan∠ABC=x,tan∠AEC=y,①求y关于x的函数解析式;②若,求y的值.
2.如图,⊙O上有A,B,C三点,AC是直径,点D是的中点,连接CD交AB于点E,点F在AB延长线上且FC=FE.
(1)证明:∠BCE=∠ACE;
(2)求证:CF是⊙O的切线;
(3)若,BE=2,求DE EC的值.
3.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)求证:CD2=CA CB;
(3)若CD=4,CB=8,求tan∠CDA的值.
4.如图,AB是半圆O的直径,AB=10.C是弧AB上一点,连接AC,BC,∠ACB的平分线交AB于点P,过点P分别作PE⊥AC,PF⊥BC,垂足分别为E、F.
(1)求证:四边形CEPF是正方形;
(2)当sinA时,求CP的长;
(3)设AP的长为x,图中阴影部分的面积为y,求y与x之间的函数关系式,并写出y的最大值.
5.如图,AC是⊙O的弦,OD⊥AC,连接OA,OC,点B在⊙O外,AB=AC,连接BC交OD于E,交OA于F,OE=OF.
(1)求证:AB是⊙O的切线;
(2)若OF=3,,求⊙O的半径.
6.如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:AB CP=BD CD;
(3)若tan∠ABC=2,AB=2,求线段DP的长.
7.如图1,在⊙O中,直径AB=10,D是AB上的动点,过点D作EF⊥AB交⊙O于点E,F连接BE,取BE的中点H,连接FH交AB于点M,并延长FH交⊙O于点C,连接CB.
(1)当点D与圆心O重合时,如图2所示,求FM FC的值.
(2)在点D的运动过程中,的值是否为定值?若是,请求出定值;若不是,请说明理由.
(3)连接OH,DH,当△ODH是等腰三角形时,求tanC的值.
8.已知在Rt△ABC中,∠ACB=90°,BC=6,AC=8,以边AC为直径作⊙O,与AB边交于点D,点M为边BC的中点,连接DM.
(1)求证:DM是⊙O的切线;
(2)点P为直线BC上任意一动点,连接AP交⊙O于点Q,连接CQ.
①当tan∠BAP时,求BP的长;
②求的最大值.
9.如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G,交AC于点H,延长AB,DC交于点E.
(1)求证:CD是⊙O的切线;
(2)求证:AF AC=AE AH;
(3)若sin∠DEA,求的值.
10.如图,在△ACB中,∠ACB=90°,O是边BC上一点,以O为圆心,OB为半径在BC边的右侧作半圆O,交AB于Q点,交BC于P点.
(1)若BC=2,当CQ取最小值时,求OC的长;
(2)已知CQ=CA,
①判断CQ与半圆O的位置关系,并说明理由;
②若OB,BQ=6,求tan∠CQA的值以及AQ的长.
11.如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F
(1)求证:ED是⊙O的切线;
(2)求证:△CFP∽△CPD;
(3)如果CF=1,CP=2,sinA,求O到DC的距离.
12.如图,已知△ABP中,C是BP边上的一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD于点F,延长CF交AB于点G,若AG AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求sin∠ACE的值.
13.如图,四边形ABDC内接于⊙O,AD是⊙O的直径,延长CD,AB交于点E,连接BC交AD于点M,过点B作BF⊥CE,垂足为点F,已知∠BDF=∠ACB.
(1)求证:BF为⊙O的切线;
(2)若OA=4,sin∠ACB,求BC的值;
(3)若CD=DF,则的值是多少?
14.如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相交于点M,连接DM,求证:DM=DC;
(3)若,求证:AM=CE.
15.如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H.
(1)求证:CD是⊙O的切线;
(2)求sin∠FHG的值;
(3)若GH=4,HB=2,求⊙O的直径.
16.如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H.
(1)求证:CD是⊙O的切线;
(2)延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;
(3)在(2)的条件下,求的值.
17.如图,四边形ABCD是⊙O的内接四边形,D是的中点,过点D作BC延长线的垂线,垂足为E,AB为⊙O的直径.
(1)求证:DE是⊙O的切线;
(2)求证:AD2=AB CE;
(3)若BC=6,tan∠A=2,求⊙O的半径.
18.如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC,AK,求BF的长.
19.如图,在Rt△ABC中,AF是⊙O的直径,BC交AF的延长线于点F.过点D的切线交BC于点B,连接OB交⊙O于点M,使∠DBO=∠CBO,BM=1.
(1)求证:BC是⊙O的切线;
(2)若CF=2,sinC,试求cos∠DBO的值.
(3)连接AD,分别延长AC,BD交于点N.当△ABC为等腰直角三角形时是否存在△CBN∽△DAN?若存在,请直接写出它们面积的相似比;若不存在,请你用反证法尝试证明.
参考答案
1.【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEC,
∵∠ADC=∠ABC,
∴∠ADC=∠DEC,
∵点D为弧AB的中点,
∴,
∴∠ACD=∠DCE,
∴△ADC∽△DEC;
(2)解:∵△ADC∽△DEC,
∴,
即CD2=CA CE,
又∵⊙O的半径为3,
∴CA CE=CD2≤62=36.
即CA CE的最大值为36;
(3)解:①∵△ADC∽△DEC,
∴,
∴y=tan∠AEC()2,
过点D作DF⊥CE,不妨设EF=a,
∵∠CED=∠CBA,∠DCE=45°,
∴CF=DF=ax,
∴CDax,
∴y=()2=()2;
②∵,
∴,
∴:8:3,
即x:y=8:3,
将yx代入y得,
x,
解得,x1=3,x2,
当x=3时,y,
当x时,y,
∴y或.
2.【解答】(1)证明:∵点D是的中点,
∴,
∴∠BCE=∠ACE;
(2)证明:∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠BEC+∠BCE=90°,
∵FC=FE,
∴∠FCE=∠FEC,
由(1)可知∠BCE=∠ACE,
∴∠FCE+∠ACE=90°,
∴∠OCF=90°,
∵OC是⊙O的半径,
∴CF是⊙O的切线;
(3)解:在Rt△FBC中,BE=2,sinF,
∴,
设BC=4x,CF=5x,
∵BC2+BF2=CF2,
∴(4x)2+(5x﹣2)2=(5x)2,
∴x=1或x(舍去),
∴BC=4,CF=5,BF=3,
∵∠CBF=∠ACF=90°,∠F=∠F,
∴△FBC∽△FCA,
∴,
∴,
∴CA,
∵sinF,
∴,
∴AF,
∴AE=AF﹣EF,
连接DA,
∵∠DAE=∠BCE,∠AED=∠CEB,
∴△AED∽△CEB,
∴,
∴AE BE=DE CE,
∴DE CE.
3.【解答】(1)证明:如图,连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
∴∠CDO=90°,
∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)证明:∵CD是⊙O的切线,
∴∠CDO=90°,
∴∠CDA+∠ADO=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DBA+∠DAB=90°,
又∵OA=OD,
∴∠DAB=∠ODA,
∴∠CDA=∠DBA,
又∵∠DCA=∠BCD,
∴△CAD∽△CDB,
∴,
∴CD2=CA CB;
(3)∵∠CDA=∠DBA,
在Rt△ABD中,tan∠CDA,
又∵,
∵CD=4,CB=8,
∴tan∠CDA.
4.【解答】(1)证明:∵∠ACB=90°,PE⊥AC,PF⊥BC,
∴四边形PECF是矩形,
∵CP平分∠ACB,PE⊥AC,PF⊥BC,
∴PE=PF,
∴四边形CEPF是正方形;
(2)解:∵sinA,AB=10,
∴,
∴BC=8,
∴AC6,
∴tanA,
设PE=CE=m,则AE=6﹣m,
∴tanA,
∴m,
∴PCPE;
(3)解:∵四边形CEPF是正方形,
∴PE=PF,∠APE+∠BPF=90°,∠PEA=∠PFB=90°,
∴将△APE绕点P顺时针旋转90°,得到△A′PF,PA′=PA,如图所示:
则A′、F、B三点共线,∠APE=∠A′PF,
∴∠A′PF+∠BPF=90°,即∠A′PB=90°,
∴S△PAE+S△PBF=S△PA′BPA′ PBx(10﹣x),
∴y与x之间的函数关系式为y5x,
∵y5x,
∴x=5时,y有最大值为.
5.【解答】(1)证明:∵OD⊥AC,
∴∠DCE+∠DEC=90°,
∵AC=AB,
∴∠ACB=∠B,
∵OE=OF,
∴∠OEF=∠OFE,
∵∠DEC=∠OEF,∠AFB=∠OFE,
∴∠DEC=∠AFB,
∴∠AFB+∠B=90°,
∴∠OAB=90°,
∵OA是⊙O的半径,
∴AB是⊙O的切线;
(2)解:∵OD⊥AC,
∴AD=CD,
Rt△ADF中,tanB,
在Rt△AOD中,
sin∠AOD,tan∠ACB,
设AD=3x,OA=5x,
∴OD4x,
∵OE=OF=3,
∴DE=4x﹣3,AF=5x﹣3,
∴AC=2AD=6x,
∴AB=6x,
∵∠ACB=∠B,
∴tan∠ACB=tanB,
∴,
∴,
解得x=1,
∴OA=5x=5,
∴⊙O的半径为5.
6.【解答】(1)证明:如图1,连接OD.
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴,
∴∠BOD=∠COD=90°,
∵BC∥PD,
∴∠ODP=∠BOD=90°,
∴OD⊥PD,
∴PD是⊙O的切线.
(2)证明:∵BC∥PD,
∴∠PDC=∠BCD.
∵∠BCD=∠BAD,
∴∠BAD=∠PDC,
∵∠ABD+∠ACD=180°,∠ACD+∠PCD=180°,
∴∠ABD=∠PCD,
∴△BAD∽△CDP,
∴,
∴AB CP=BD CD;
(3)解:∵BC是⊙O的直径,
∴∠BAC=90°,
∵tan∠ABC=2,,
∴2,
∴,
∴,
∴OD=5,
如图2,连接OD,过点C作CG⊥DP,垂足为G,则四边形ODGC为正方形,
∴DG=CG=OD=5,
∵BC∥PD,
∴∠CPG=∠ACB,
∴tan∠CPG=tan∠ACB,
∴,即,
解得,GP=10,
∴DP=DG+PG=5+10=15.
7.【解答】解:(1)连接CE,
∵AB=10,
∴OF=OE=5,
∵EF是直径,
∴∠ECF=90°,
∵∠MFO=∠EFC,∠MOF=∠ECF=90°,
∴△MOF∽△ECF,
∴,
∴FM CF=EF OF=50;
(2)是定值,理由如下:
过点H作HN⊥EF,垂足为点N,
∵EF⊥AB,
∴DE=DF,
设DE=DF=2x,
∵点H是BE中点,
∴,
∵HN⊥EF,EF⊥AB,
∴HN∥AB,
∴,
∴EN=DN,
∴DNDE=x,
∴FN=DF+DN=3x,
∵HN∥AB,
∴△FMD∽△FHN,
∴,
∴;
(3)若点D在点O的左侧,此时有OD=OH,连接OE,
∵点H是BE的中点,
∴OH⊥BE,
∵∠EDO=∠EHO,OD=OH,EO=EO,
∴Rt△DOE≌△HOE(HL),
∴DE=EH,
在Rt△BDE中,
∵点H是BE的中点,
∴DH=EH=BH,
∴DE=DH=EH,
∴△DHE是等边三角形,
∴∠BEF=60°,
∵,
∴∠C=∠BEF=60°,
∴tanC;
若点D在点O的右侧,此时有OD=DH,
∵点H是BE中点,
∴OH⊥BE,
∴∠OHB=90°,
∴∠HOB+∠OBH=90°,∠OHD+∠DHB=90°,
∵OD=DH,
∴∠HOB=∠OHD,
∴∠OBH=∠DHB,
∴DH=BD,
在Rt△BDE中,
∵点H是BE的中点,
∴DH=BH=EH,
∴DH=BD=BH,
∴△BDH是等边三角形,
∴∠DBE=60°,
∴∠BEF=30°,
∵,
∴∠C=∠BEF=30°,
∴tanC;
综上所述,当△ODH是等腰三角形时,tanC或.
8.【解答】(1)证明:如图,连接OD,CD,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠BDC=180°﹣∠ADC=90°,
∵点M为边BC的中点,
∴MC=MD,
∴∠MDC=∠MCD,
∵OC=OD,
∴∠ODC=∠OCD,
∵∠ACB=90°,即∠MCD+∠OCD=90°,
∴∠MDC+ODC=∠MCD+∠OCD=90°,
即∠ODM=90°,
∴DM⊥OD,
∵OD是⊙O的半径,
∴DM是⊙O的切线;
(2)①当点P在线段BC上时,如图,过点P作PT⊥AB于点T,
在Rt△ABC中,AB10,
设PT=x,
∵tan∠BAP,
∴,
∴AT=3PT=3x,
∴BT=AB﹣AT=10﹣3x,
∵tan∠ABC,
∴,
解得:x,
∴PT,
∵sin∠ABC,即,
∴BP;
当点P在CB的延长线上时,如图,过点B作BK⊥AP于点K,
∵tan∠BAP,
∴,
设BK=a,则AK=3a,
在Rt△ABK中,AK2+BK2=AB2,
即(3a)2+a2=102,
解得:a1,a2(舍去),
∴AK=3,BK,
∵S△ABPAP BKBP AC,
∴,
设BP=m,则APm,
在Rt△ACP中,AC2+CP2=AP2,
即82+(m+6)2=(m)2,
解得:m1,m2(舍去),
∴BP;
综上所述,BP的长为或;
②设CP=n,则AP,
如图,∵AC是⊙O的直径,
∴CQ⊥AP,
∵CQ AP=AC CP,
∴CQ,
∴,
∵n>0,
∴(n﹣8)2≥0,
∴64+n2≥16n,
∴,
∴的最大值为.
9.【解答】(1)证明:连接OC,
∵AC平分∠DAB,
∴∠DAC=∠EAC,
∵∠OCA=∠EAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵CD⊥AD,
∴OC⊥AD,
∵OC是半径,
∴CD是⊙O的切线;
(2)证明:∵AC平分∠DAB,
∴∠DAC=∠EAC,
又∵CD⊥AD,FG⊥AB,
∴∠AGF=∠D=90°,
∴∠AFG+∠DAG=90°,∠E+∠DAE=90°,
∴∠AFG=∠DEA,
∴△AHF∽△ACE,
∴,
即AF AC=AE AH;
(3)过H作HM⊥AD,如图:
由(2)知∠AFG=∠DEA,
∴sin∠DEAsin∠AFG,
设AG=4x,AF=5x,则FG=3x,
∵AC平分∠DAB,
∴MH=GH,AG=AM=4x,
∴MF=x,
设GH=MH=a,
∴tan∠AFG,
∴,
∴ax,
∴FH=3xxx,
AH,
∴.
10.【解答】解:(1)当CQ取最小值时,CQ⊥AB,此时P点与C点重合,O是BC的中点,
∵BC=2,
∴OC=1;
(2)①CQ与半圆O相切,
理由如下:连接OQ,
∵OB=OQ,
∴∠B=∠OQB,
∵CQ=CA,
∴∠CQA=∠A,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠OQB+∠CQA=90°,
∴∠OQC=180°﹣(∠OQB+∠CQA)=90°,
∴OQ⊥QC,
又∵OQ是圆的半径,
∴CQ与半圆O相切;
②如图,连接PQ,过C作CD⊥AB于D,
由题意得,BP=2OB=15,BQ,
∵BP是直径,
∴∠BQP=90°,
∴PQ,
∵∠PQA+∠A+∠PCA+∠CPQ=360°,
∴∠A+∠CPQ=180°,
∵∠CPQ+∠BPQ=180°,
∴∠A=∠BPQ,
∵CQ=CA,
∴∠A=∠CQA,
∴tan∠CQA=tan∠BPQ,
∵CQ=CA,
∴QD=DA,
设QD=a,
∵tan∠CQA2,
∴CD=2a,
∵∠PQB=∠CDB=90°,
∴PQ∥CD,
∴∠BPQ=∠BCD,
∴tan∠BCD=tan∠BPQ=2,
∴BD=4a,
∴BQ=3a,
∴a,
∴AQ.
11.【解答】(1)证明:连接OD.
∵BC为直径,
∴△BDC为直角三角形.
在Rt△ADB中,E为AB中点,
∴BE=DE,
∴∠EBD=∠EDB.
又∵OB=OD,∴∠OBD=∠ODB,
∵∠OBD+∠ABD=90°,∴∠ODB+∠EDB=90°.
∴ED是⊙O的切线.
(2)证明:∵PF⊥BC,
∴∠FPC=90°﹣∠BCP(直角三角形的两个锐角互余).
∵∠PDC=90°﹣∠PDB(直径所对的圆周角是直角),∠PDB=∠BCP(同弧所对的圆周角相等),
∴∠FPC=∠PDC(等量代换).
又∵∠PCF是公共角,
∴△PCF∽△DCP.
(3)解:过点O作OM⊥CD于点M,
∵△PCF∽△DCP,
∴PC2=CF CD(相似三角形的对应边成比例).
∵CF=1,CP=2,
∴CD=4.
可知sin∠DBC=sinA=sin∠MOC,
∴,即,
∴直径BC=5,
∴,
∴MC=2,
∴MO,
∴O到DC的距离为.
12.【解答】(1)证明:连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠ADC=90°.
∵∠PAC=∠PBA,∠ADC=∠PBA,
∴∠PAC=∠ADC,
∴∠CAD+∠PAC=90°,
∴PA⊥OA,而AD是⊙O的直径,
∴PA是⊙O的切线;
(2)解:由(1)知,PA⊥AD,
∵CF⊥AD,
∴CF//PA,
∴∠GCA=∠PAC.
∵∠PAC=∠PBA,
∴∠GCA=∠PBA.
又∵∠CAG=∠BAC,
∴△CAG∽△BAC,
∴,
即AC2=AG AB.
∵AG AB=12,
∴;
(3)解:∵AF:FD=1:2,
设AF=x,FD=2x,则AD=AF+FD=3x.
在Rt△ACD 中,
∵CF⊥AD,
∴∠AFC=∠ACD=90°.
又∵∠CAF=∠DAC,
∴△CAF∽△DAC,
∴,
∴AC2=AF AD,
即3x2=12,
解得x=2,
∴AF=2,FD=4,AD=6.
在Rt△AFG 中,
∵AF=2,GF=1,
∴.
由(2)知,AG AB=12,
∴.
连接BD,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴.
∵∠ACE=∠ACB=∠ADB,
∴.
13.【解答】(1)证明:连接OB.
∵四边形ABDC内接于⊙O,
∴∠BDC+∠BAC=180°,
∵∠BDF+∠BDC=180°,
∴∠BAC=∠BDF,
∵∠BDF=∠ACB.
∴∠BAC=∠ACB,
∴AB=CB,
∵AC⊥CE,
∴∠ACE=90°,
∴∠E+∠EAC=90°,∠BCE+∠ACB=90°,
∴∠E=∠BCE,
∴EB=CB,
∴AB=BE,
∴OB是△ADE的中位线.
∴OB∥CE,
∵BF⊥CE,
∴BF⊥OB,
∴BF为⊙O的切线;
(2)解:∵AD是直径,
∴∠ABD=90°,
∵∠ADB=∠ACB,
∴sin∠ACB=sin∠ADB,
∵AD=2OA=8,
∴AB=6,
∴BC=AB=6;
(3)解:设CD=DF=a,
由(2)知BE=BC.
又∵BF⊥CE,
∴CF=EF=2a
∴DE=3a,
由(1)可知,OB是△ADE的中位线,
∴OB∥DE且OBDE,
∴△BOM∽△CDM.
∴,
∴.
14.【解答】证明:(1)如图所示,连接OD,
∵AB=AC,OB=OD,
∴∠C=∠B=∠ODB,
∵DE⊥AC,即∠DEC=90°,
∴∠C+∠CDE=90°,
∴∠ODB+∠CDE=90°,
∴∠ODE=90°,
∴OD⊥OE,
又∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)如图所示,连接OM,
∵OA=OM,
∴∠OAM=∠OMA,
∵OD⊥DE,AC⊥DE,
∴AC∥OD,
∴∠BOD=∠OAM=∠DOM=∠OMA,∠ODM=∠DMC,∠C=∠ODB,
∵OB=OD=OM,
∴△OBD≌△OMD(SAS),
∴∠ODB=∠ODM=∠DMC,
∴∠DMC=∠C,
∴DM=DC;
(3)∵AB是直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=CD,
在Rt△ABD中,,
∴可设,
∴,
∵∠CDE+∠C=90°=∠BAD+∠B,∠B=∠C,
∴∠CDE=∠BAD,
∴sin∠CDE=sin∠BAD,
在Rt△CDE中,,
∵DM=DC,DE⊥CM,
∴,
∴,
∴AM=CE.
15.【解答】(1)证明:连接OF.
∵OA=OF,
∴∠OAF=∠OFA,
∵,
∴∠CAF=∠FAB,
∴∠CAF=∠AFO,
∴OF∥AC,
∵AC⊥CD,
∴OF⊥CD,
∵OF是半径,
∴CD是⊙O的切线.
(2)解:∵AB是直径,
∴∠AFB=90°,
∵OF⊥CD,
∴∠OFD=∠AFB=90°,
∴∠AFO=∠DFB,
∵∠OAF=∠OFA,
∴∠DFB=∠OAF,
∵GD平分∠ADF,
∴∠ADG=∠FDG,
∵∠FGH=∠OAF+∠ADG,∠FHG=∠DFB+∠FDG,
∴∠FGH=∠FHG=45°,
∴sin∠FHG;
(3)解:过点H作HM⊥DF于点M,HN⊥AD于点N.
∵HD平分∠ADF,
∴HM=HN,
∵,
∵△FGH是等腰直角三角形,GH=4,
∴FH=FG=4,
∴2,
设DB=k,DF=2k,
∵∠FDB=∠ADF,∠DFB=∠DAF,
∴△DFB∽△DAF,
∴DF2=DB DA,
∴AD=4k,
∵GD平分∠ADF,
∴∠FDH=∠ADG,
∴△FDH∽△ADG,
∴,
∴AG=8,
∵∠AFB=90°,AF=12,FB=6,
∴AB6,
∴⊙O的直径为6.
解法二:由(2)可知sin∠FHG,
∴FH=FG=4,
∴FB=FH+HB=4+2=6,2,
∵DG是∠FDA的角平分线,
可证2,
∵△DAF∽△DFB,
∴,
∴AF=12,
∵∠AFB=90°,AF=12,FB=6,
∴AB6.
解法三:可以作GP⊥AF交AD于点P,再证△DFG≌△DGP,△AGP∽△AFB可以求出AF的长,用勾股定理求出直径AB的长.
16.【解答】(1)证明:如图1,连接OC,
∵OA=OC,
∴∠CAO=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠ACO,
∴AD∥OC,
∵CD⊥AD,
∴OC⊥CD,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)解:∵AE=4BE,OA=OB,
设BE=x,则AB=3x,
∴OC=OB=1.5x,
∵AD∥OC,
∴∠COE=∠DAB,
∴cos∠DAB=cos∠COE;
(3)解:由(2)知:OE=2.5x,OC=1.5x,
∴EC2x,
∵FG⊥AB,
∴∠AGF=90°,
∴∠AFG+∠FAG=90°,
∵∠COE+∠E=90°,∠COE=∠DAB,
∴∠E=∠AFH,
∵∠FAH=∠CAE,
∴△AHF∽△ACE,
∴.
17.【解答】(1)证明:连接OD,BD,如图,
∵DE⊥BE,
∴∠EDB+∠EBD=90°.
∵D是的中点,
∴∠EBD=∠ABD.
∵OD=OB,
∴∠ABD=∠ODB.
∴∠ODB=∠EBD.
∴∠ODB+∠EDB=90°.
即OD⊥DE.
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∵四边形ABCD为⊙O的内接四边形,
∴∠ECD=∠A.
∵DE⊥BE,
∴∠DEC=90°.
∴∠ADB=∠DEC.
∴△ABD∽△CDE.
∴.
∵D是的中点,
∴.
∴AD=CD
∴.
∴AD2=AB CE;
(3)解:∵∠ECD=∠A,tan∠A=2,
∴tan∠ECD.
∴DE=2CE.
∵△ABD∽△CDE,
∴∠EDC=∠ABD=∠EBD.
∵∠E=∠E,
∴△EDC∽△EBD.
∴.
∴ED2=EC EB.
∵BC=6,
∴4EC2=EC(EC+6).
∵EC≠0
∴EC=2,DE=4.
∴BD2=DE2+BE2=64+16=80.
∵CD2=DE2+CE2=16+4=20,
∴AD2=20.
∵AD2=AB CE,
∴AB10.
∴OA=5.
∴⊙O的半径为5.
18.【解答】解:(1)如图,连接OG.
∵EG=EK,
∴∠KGE=∠GKE=∠AKH,
又OA=OG,
∴∠OGA=∠OAG,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
∴∠KGE+∠OGA=90°,
∴EF是⊙O的切线.
(2)①∵AC∥EF,
∴∠E=∠C,
又∠C=∠AGD,
∴∠E=∠AGD,
又∠DKG=∠GKE,
∴△KGD∽△KEG;
②连接OG,
∵,AK,
设cosC,
∴CH=4k,AC=5k,则AH=3k,
∵KE=GE,AC∥EF,
∴CK=AC=5k,
∴HK=CK﹣CH=k.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即,
解得k=1,
∴CH=4,AC=5,则AH=3,
设⊙O半径为R,在Rt△OCH中,OC=R,OH=R﹣3k,CH=4k,
由勾股定理得:OH2+CH2=OC2,即(R﹣3)2+42=R2,
∴,
在Rt△OGF中,,
∴,
∴.
19.【解答】(1)证明:方法一:
连接OD,过点O作OE⊥BC于点E,如图,
∵BD为⊙O的切线,
∴OD⊥BD,
∴∠ODB=90°.
∵OE⊥BC,
∴∠OEB=90°.
∴∠ODB=∠OEB.
在△ODB和△OEB中,
,
∴△ODB≌△OEB(AAS),
∴OD=OE.
即OE为⊙O的半径,
∴BC是⊙O的切线;
方法二:
连接OD,过点O作OE⊥BC于点E,如图,
∵BD为⊙O的切线,
∴OD⊥BD,
∵∠DBO=∠CBO,OE⊥BC,
∴OD=OE.
即OE为⊙O的半径,
∴BC是⊙O的切线;
(2)解:在Rt△OEC中,
∴sinC,
∵sinC,
∴,
设OE=2k,则OC=5k,
∵OF=OE=2k,
∴CF=OC﹣OF=3k=2,
∴k.
∴OE=2k,
∴OM=OE.
∴OB=OM+MB=1.
∴BE.
∴cos∠EBO.
∵∠DBO=∠CBO,
∴cos∠DBO=cos∠CBO;
(3)解:当△ABC为等腰直角三角形时,不存在△CBN∽△DAN,理由:
用反证法:
假设△CBN∽△DAN,如图,
∵△ABC为等腰直角三角形,
∴∠C=∠BAC=45°,
∵CBN∽△DAN,
∴∠ADN=∠C=45°.
∵BD为⊙O的切线,
∴OD⊥BD,
∴∠ODN=90°,
∴∠ODA=90°﹣∠ADN=45°.
∵OD=OA,
∴∠OAD=∠ODA=45°,
∴∠AOD=90°,
∴OD⊥AC,
∵OD⊥BN,
∴AC∥BD,
这与BD与AC相交于点N矛盾,
∴假设不成立,
∴当△ABC为等腰直角三角形时,不存在△CBN∽△DAN.
21世纪教育网(www.21cnjy.com)
同课章节目录
