人教版八年级数学下册 17.1 勾股定理 同步练习(含解析)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 19:31:53 | ||
图片预览


文档简介
17.1 勾股定理
一、单选题
1.如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是( )
A.(5,0) B.(8,0) C.(0,5) D.(0,8)
2.如图,海中有一小岛A,在B点测得小岛A在北偏东30°方向上,渔船从B点出发由西向东航行10到达C点,在C点测得小岛A恰好在正北方向上,此时渔船与小岛A的距离为( )
A. B. C.20 D.
3.如图,在中,,点在边上,且平分的周长,则的长是( )
A. B. C. D.
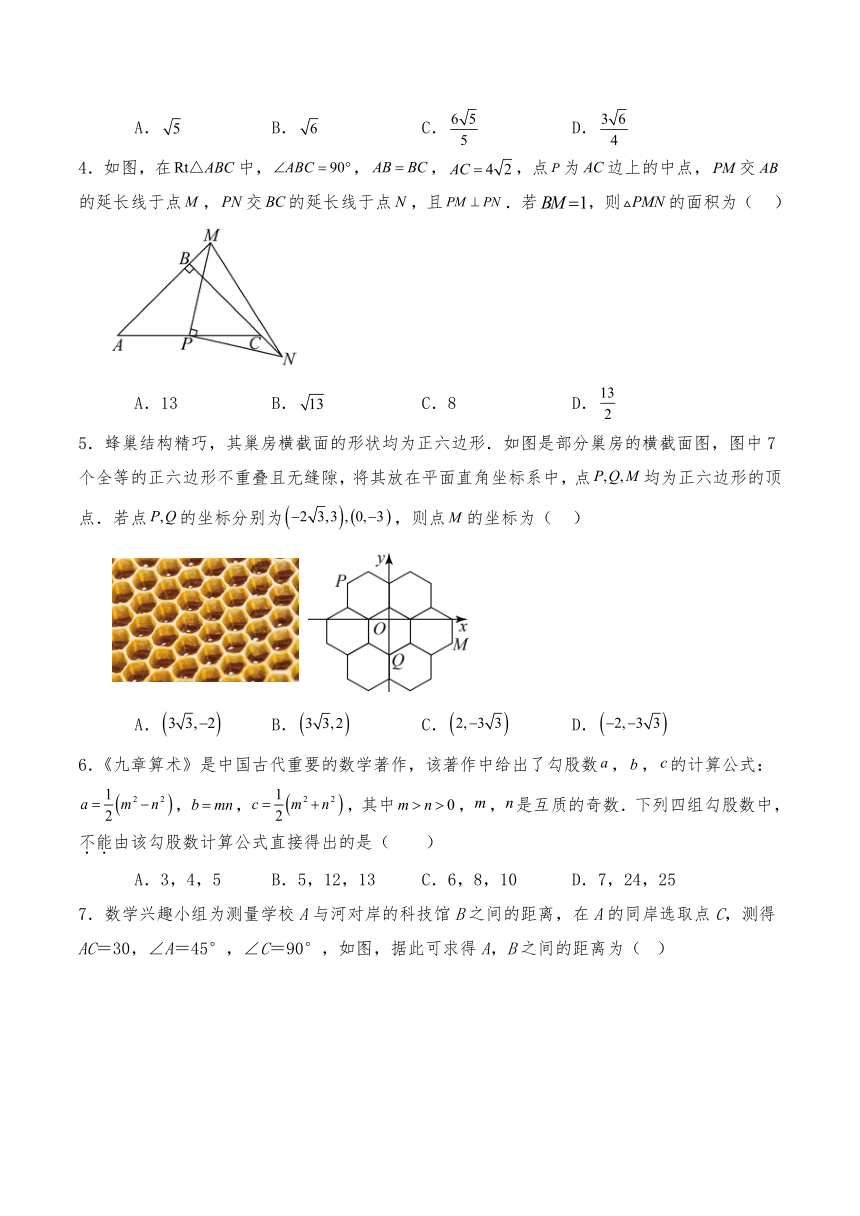
4.如图,在中,,,,点为边上的中点,交的延长线于点,交的延长线于点,且.若,则的面积为( )
A.13 B. C.8 D.
5.蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为,则点的坐标为( )
A. B. C. D.
6.《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数,,的计算公式:,,,其中,,是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )
A.3,4,5 B.5,12,13 C.6,8,10 D.7,24,25
7.数学兴趣小组为测量学校A与河对岸的科技馆B之间的距离,在A的同岸选取点C,测得AC=30,∠A=45°,∠C=90°,如图,据此可求得A,B之间的距离为( )
A.20 B.60 C.30 D.30
8.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
9.如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若,,则点到的距离为( )
A. B. C.1 D.2
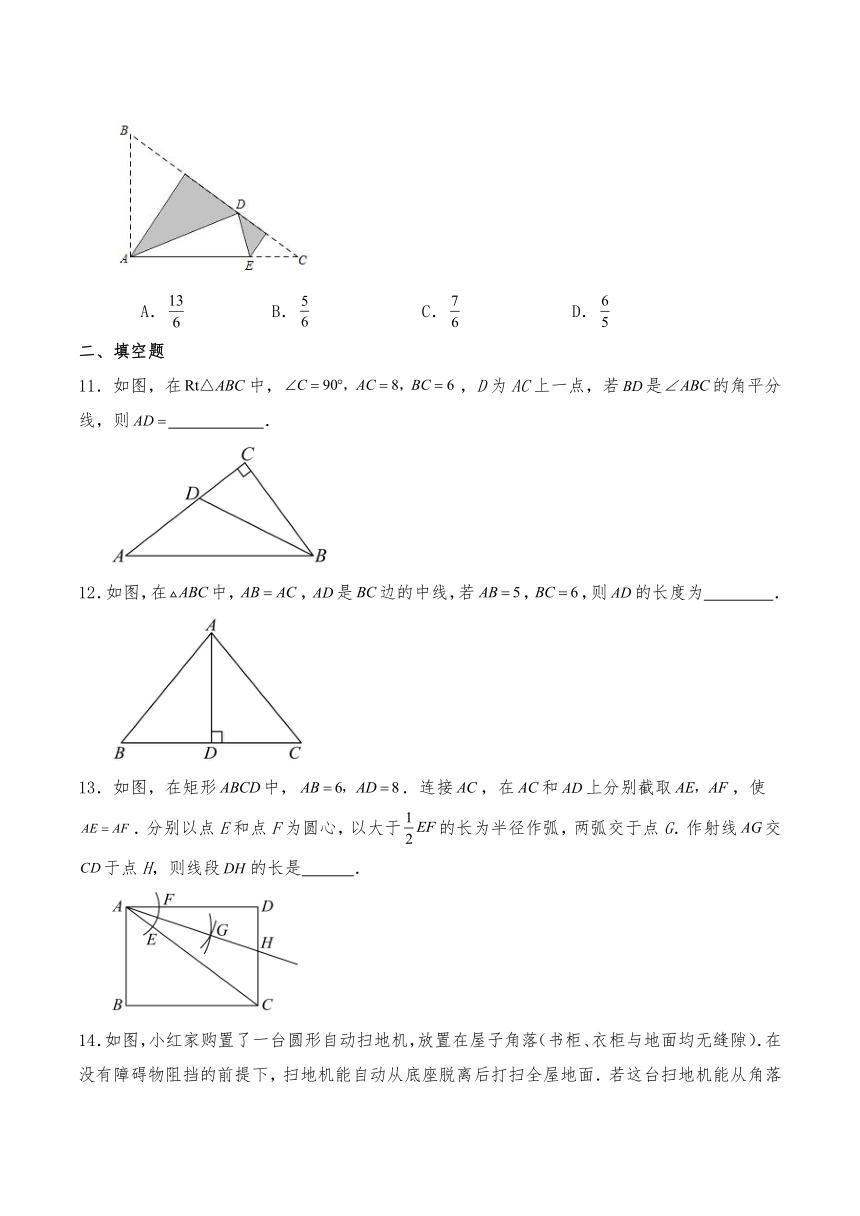
10.如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A. B. C. D.
二、填空题
11.如图,在中,,D为AC上一点,若是的角平分线,则 .
12.如图,在中,,是边的中线,若,,则的长度为 .
13.如图,在矩形中,.连接,在和上分别截取,使.分别以点E和点F为圆心,以大于的长为半径作弧,两弧交于点G.作射线交于点H,则线段的长是 .
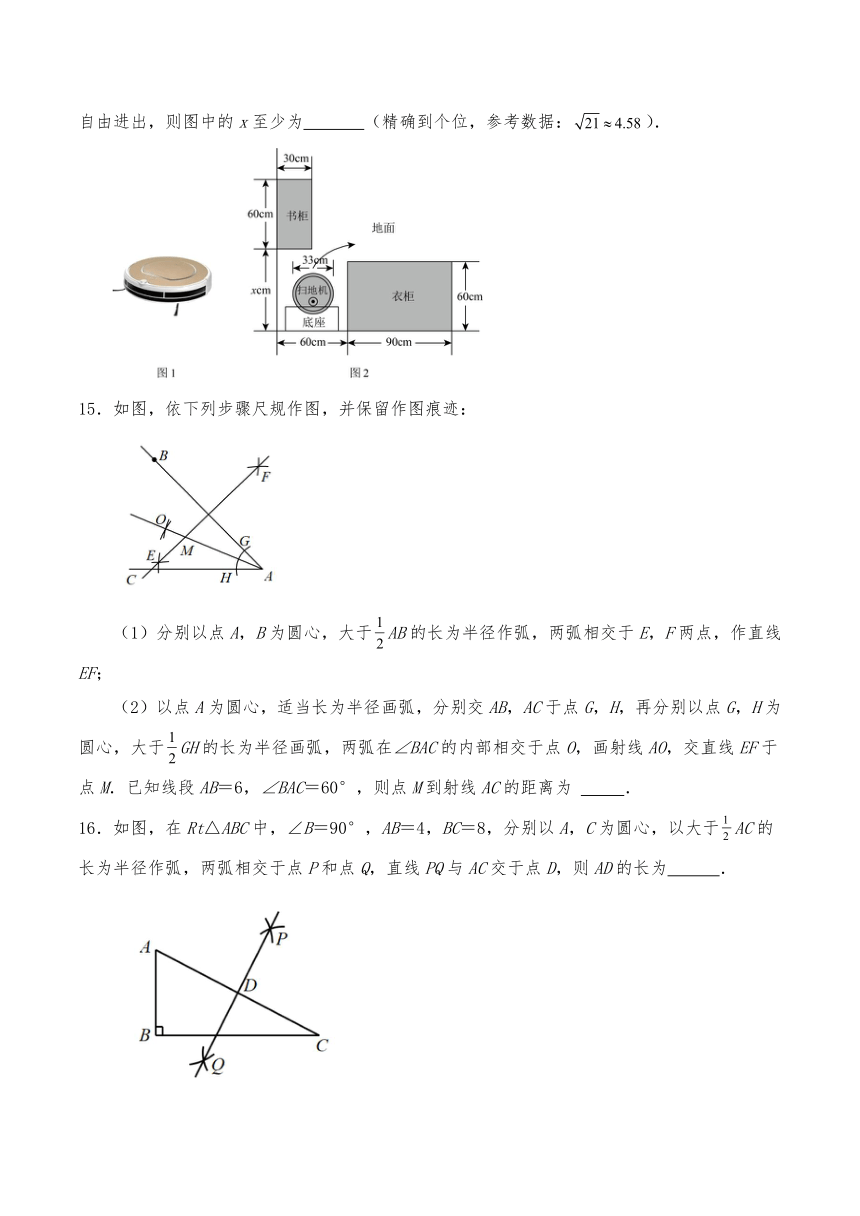
14.如图,小红家购置了一台圆形自动扫地机,放置在屋子角落(书柜、衣柜与地面均无缝隙).在没有障碍物阻挡的前提下,扫地机能自动从底座脱离后打扫全屋地面.若这台扫地机能从角落自由进出,则图中的x至少为 (精确到个位,参考数据:).
15.如图,依下列步骤尺规作图,并保留作图痕迹:
(1)分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于E,F两点,作直线EF;
(2)以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为 .
16.如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .
17.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
18.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
三、解答题
19.如图,方格纸中每个小正方形的边长均为个单位长度,线段和线段的端点均在小正方形的顶点上.
(1)在方格纸中画出,且为钝角(点在小正方形的顶点上);
(2)在方格纸中将线段向下平移个单位长度,再向右平移个单位长度后得到线段(点的对应点是点,点的对应点是点),连接,请直接写出线段的长.
20.如图,,,,垂足分别为,.
(1)求证:;
(2)若,,求的长.
21.如图是“弦图”的示意图,“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,它标志着中国古代的数学成就.它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,每个直角三角形的两条直角边分别为a、b,斜边为c.请你运用此图形证明勾股定理:a2+b2=c2.
22.如图,在中,,,是边上的一点,以为直角边作等腰,其中,连接.
(1)求证:;
(2)若时,求的长.
23.某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线,点A、B分别在、上,斜坡AB的长为18米,过点B作于点C,且线段AC的长为米.
(1)求该斜坡的坡高BC;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚为60°,过点M作于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
答案:
一、单选题
1.B
解:∴AO=3,BO=4,
∴AB=AB′=5,故OB′=8,
∴点B′的坐标是(8,0).
故选:B.
2.D
【分析】连接,此题易得,得,再利用勾股定理计算即可.
解:连接,
由已知得:,,,
∴,
在中,,
∴(),
故选:D
3.C
【分析】如图所示,过点B作于E,利用勾股定理求出,进而利用等面积法求出,则可求出,再由平分的周长,求出,进而得到,则由勾股定理得.
解:如图所示,过点B作于E,
∵在中,,
∴,
∵,
∴,
∴,
∵平分的周长,
∴,即,
又∵,
∴,
∴,
∴,
故选C.
4.D
【分析】依据题意,连接,然后先证明,从而,又由等腰可得,从而在中可以求得,又,从而可得的值,进而可以得解.
解:如图,连接.
在中,,
,点为边上的中点,
,,,.
.
,,
,.
.
又,,
.
,.
在中,.
在中,.
又在中,,
.
.
.
故选:D.
5.A
【分析】连接,设正六边形的边长为a,由正六边形的性质及点P的坐标可求得a的值,即可求得点M的坐标.
解:连接,如图,设正六边形的边长为a,
∵,
∴,
∵,
∴,
∴,
∴,,
∵点P的坐标为,
∴,
即;
∴,,
∴点M的坐标为.
故选:A.
6.C
【分析】首先证明出,得到a,b是直角三角形的直角边然后由,,是互质的奇数逐项求解即可.
解:∵,
∴.
∵,
∴.
∴a,b是直角三角形的直角边,
∵,是互质的奇数,
∴A.,
∴当,时,,,,
∴3,4,5能由该勾股数计算公式直接得出;
B.,
∴当,时,,,,
∴5,12,13能由该勾股数计算公式直接得出;
C.,,
∵,是互质的奇数,
∴6,8,10不能由该勾股数计算公式直接得出;
D.,
∴当,时,,,,
∴7,24,25能由该勾股数计算公式直接得出.
故选:C.
7.C
【分析】根据等腰直角三角形的性质,利用勾股定理计算即可求解.
解:在Rt△ABC中,∠C=90°,∠A=45°,AC=30,
∴∠B=∠A=45°,
∴BC=AC=30,
∴AB=,
故选:C
8.B
【分析】根据图形分析可得小正方形的边长为两条直角边长的差,据此即可求解.
解:图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是.
故选B.
9.B
【分析】根据题意求得,进而求得,进而等面积法即可求解.
解:在中,
,,
,
,
设到的距离为,
,
,
故选B.
10.A
【分析】根据题意可得AD = AB = 2, ∠B = ∠ADB, CE= DE, ∠C=∠CDE,可得∠ADE = 90°,继而设AE=x,则CE=DE=3-x,根据勾股定理即可求解.
解:∵沿过点A的直线将纸片折叠,使点B落在边BC上的点D处,
∴AD = AB = 2, ∠B = ∠ADB,
∵折叠纸片,使点C与点D重合,
∴CE= DE, ∠C=∠CDE,
∵∠BAC = 90°,
∴∠B+ ∠C= 90°,
∴∠ADB + ∠CDE = 90°,
∴∠ADE = 90°,
∴AD2 + DE2 = AE2,
设AE=x,则CE=DE=3-x,
∴22+(3-x)2 =x2,
解得
即AE=
故选A
二、填空题
11.5
【分析】首先证明,,设,在中,利用勾股定理构建方程即可解决问题.
解:如图,过点D作的垂线,垂足为P,
在中,∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
∴,,
设,
在中,∵,,
∴,
∴,
∴.
故答案为:5.
12.4
【分析】根据等腰三角形的性质和勾股定理求解即可.
解:∵在中,,是边的中线,
∴,,
在中,,,
∴,
故答案为:4.
13.
【分析】过H作于Q,再根据角平分线的性质和勾股定理列方程求解.
解:设,
过H作于Q,
在矩形中,,
∴,
由作图得:平分,
∴,
∵,,
∴,
∴,
∴,
在中,有,
即:,
解得:,
故答案为:.
14.
【分析】先建立直角三角形,利用勾股定理解决实际问题.
解:如图过点A、B分别作墙的垂线,交于点C,
则,,
在中,,
即
∵这台扫地机能从角落自由进出,
∴这台扫地机的直径不小于长,
即最小时为,
解得:(舍),,
∴图中的x至少为,
故答案为:.
15.
【分析】根据线段的垂直平分线和角平分线的作法可知:EF是线段AB的垂直平分线,AO是∠AOB的平分线,利用线段的垂直平分线的性质和角平分线的性质的求解即可.
解:如图所示:
根据题意可知:EF是线段AB的垂直平分线,AO是∠BAC的平分线,
∵AB=6,∠BAC=60°,
∴∠BAO=∠CAO=∠BAC=30°,AD=AB=3,
∴AM=2MD,
在Rt△ADM中,,
即,
∴MD=,
∵AM是∠AOB的平分线,MD⊥AB,
∴点M到射线AC的距离为.
故答案为:.
16.
【分析】利用勾股定理求出AC,再利用线段的垂直平分线的性质求出AD.
解:在Rt△ABC中,∠B=90°,AB=4,BC=8,
∴AC===4,
由作图可知,PQ垂直平分线段AC,
∴AD=DC=AC=2,
故答案为:2.
17.m2+1
【分析】2m为偶数,设其股是a,则弦为a+2,根据勾股定理列方程即可得到结论.
解:∵2m为偶数,
∴设其股是a,则弦为a+2,
根据勾股定理得,(2m)2+a2=(a+2)2,
解得a=m2-1,
∴弦长为m2+1,
故答案为:m2+1.
18.127
【分析】由已知图形观察规律,即可得到第六代勾股树中正方形的个数.
解:∵第一代勾股树中正方形有1+2=3(个),
第二代勾股树中正方形有1+2+22=7(个),
第三代勾股树中正方形有1+2+22+23=15(个),
......
∴第六代勾股树中正方形有1+2+22+23+24+25+26=127(个),
故答案为:127.
三、解答题
19.
(1)解:如图所示,即为所求;
(2)解:如图所示,,即为所求;
.
20.
解:(1)证明:,,
,
在和中,
,
;
(2)解:,
,
在中,,
,
.
21.
解:由题意得大正方形面积,小正方形面积,
4个小直角三角形的面积,
∵大正方形的面积=小正方形的面积+4个直角三角形的面积,
∴.
22.
解:(1)证明:∵ ADE是等腰直角三角形,
,
,
,
在与中
;
,
(2)在中,,,
,
,
,
,
,
∴∠ADC=∠ACD,
,
.
23.
解:(1)在Rt△ABC中,;
(2)∵,
∴,
∴,
∵在Rt△ABC中,,
∴
∴,
∴,∴.
综上所述,长度增加了2米.
一、单选题
1.如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是( )
A.(5,0) B.(8,0) C.(0,5) D.(0,8)
2.如图,海中有一小岛A,在B点测得小岛A在北偏东30°方向上,渔船从B点出发由西向东航行10到达C点,在C点测得小岛A恰好在正北方向上,此时渔船与小岛A的距离为( )
A. B. C.20 D.
3.如图,在中,,点在边上,且平分的周长,则的长是( )
A. B. C. D.
4.如图,在中,,,,点为边上的中点,交的延长线于点,交的延长线于点,且.若,则的面积为( )
A.13 B. C.8 D.
5.蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为,则点的坐标为( )
A. B. C. D.
6.《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数,,的计算公式:,,,其中,,是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )
A.3,4,5 B.5,12,13 C.6,8,10 D.7,24,25
7.数学兴趣小组为测量学校A与河对岸的科技馆B之间的距离,在A的同岸选取点C,测得AC=30,∠A=45°,∠C=90°,如图,据此可求得A,B之间的距离为( )
A.20 B.60 C.30 D.30
8.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )
A.4 B.8 C.12 D.16
9.如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若,,则点到的距离为( )
A. B. C.1 D.2
10.如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A. B. C. D.
二、填空题
11.如图,在中,,D为AC上一点,若是的角平分线,则 .
12.如图,在中,,是边的中线,若,,则的长度为 .
13.如图,在矩形中,.连接,在和上分别截取,使.分别以点E和点F为圆心,以大于的长为半径作弧,两弧交于点G.作射线交于点H,则线段的长是 .
14.如图,小红家购置了一台圆形自动扫地机,放置在屋子角落(书柜、衣柜与地面均无缝隙).在没有障碍物阻挡的前提下,扫地机能自动从底座脱离后打扫全屋地面.若这台扫地机能从角落自由进出,则图中的x至少为 (精确到个位,参考数据:).
15.如图,依下列步骤尺规作图,并保留作图痕迹:
(1)分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于E,F两点,作直线EF;
(2)以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为 .
16.如图,在Rt△ABC中,∠B=90°,AB=4,BC=8,分别以A,C为圆心,以大于AC的长为半径作弧,两弧相交于点P和点Q,直线PQ与AC交于点D,则AD的长为 .
17.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
18.“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
三、解答题
19.如图,方格纸中每个小正方形的边长均为个单位长度,线段和线段的端点均在小正方形的顶点上.
(1)在方格纸中画出,且为钝角(点在小正方形的顶点上);
(2)在方格纸中将线段向下平移个单位长度,再向右平移个单位长度后得到线段(点的对应点是点,点的对应点是点),连接,请直接写出线段的长.
20.如图,,,,垂足分别为,.
(1)求证:;
(2)若,,求的长.
21.如图是“弦图”的示意图,“弦图”最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的,它标志着中国古代的数学成就.它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形,每个直角三角形的两条直角边分别为a、b,斜边为c.请你运用此图形证明勾股定理:a2+b2=c2.
22.如图,在中,,,是边上的一点,以为直角边作等腰,其中,连接.
(1)求证:;
(2)若时,求的长.
23.某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线,点A、B分别在、上,斜坡AB的长为18米,过点B作于点C,且线段AC的长为米.
(1)求该斜坡的坡高BC;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚为60°,过点M作于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
答案:
一、单选题
1.B
解:∴AO=3,BO=4,
∴AB=AB′=5,故OB′=8,
∴点B′的坐标是(8,0).
故选:B.
2.D
【分析】连接,此题易得,得,再利用勾股定理计算即可.
解:连接,
由已知得:,,,
∴,
在中,,
∴(),
故选:D
3.C
【分析】如图所示,过点B作于E,利用勾股定理求出,进而利用等面积法求出,则可求出,再由平分的周长,求出,进而得到,则由勾股定理得.
解:如图所示,过点B作于E,
∵在中,,
∴,
∵,
∴,
∴,
∵平分的周长,
∴,即,
又∵,
∴,
∴,
∴,
故选C.
4.D
【分析】依据题意,连接,然后先证明,从而,又由等腰可得,从而在中可以求得,又,从而可得的值,进而可以得解.
解:如图,连接.
在中,,
,点为边上的中点,
,,,.
.
,,
,.
.
又,,
.
,.
在中,.
在中,.
又在中,,
.
.
.
故选:D.
5.A
【分析】连接,设正六边形的边长为a,由正六边形的性质及点P的坐标可求得a的值,即可求得点M的坐标.
解:连接,如图,设正六边形的边长为a,
∵,
∴,
∵,
∴,
∴,
∴,,
∵点P的坐标为,
∴,
即;
∴,,
∴点M的坐标为.
故选:A.
6.C
【分析】首先证明出,得到a,b是直角三角形的直角边然后由,,是互质的奇数逐项求解即可.
解:∵,
∴.
∵,
∴.
∴a,b是直角三角形的直角边,
∵,是互质的奇数,
∴A.,
∴当,时,,,,
∴3,4,5能由该勾股数计算公式直接得出;
B.,
∴当,时,,,,
∴5,12,13能由该勾股数计算公式直接得出;
C.,,
∵,是互质的奇数,
∴6,8,10不能由该勾股数计算公式直接得出;
D.,
∴当,时,,,,
∴7,24,25能由该勾股数计算公式直接得出.
故选:C.
7.C
【分析】根据等腰直角三角形的性质,利用勾股定理计算即可求解.
解:在Rt△ABC中,∠C=90°,∠A=45°,AC=30,
∴∠B=∠A=45°,
∴BC=AC=30,
∴AB=,
故选:C
8.B
【分析】根据图形分析可得小正方形的边长为两条直角边长的差,据此即可求解.
解:图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是.
故选B.
9.B
【分析】根据题意求得,进而求得,进而等面积法即可求解.
解:在中,
,,
,
,
设到的距离为,
,
,
故选B.
10.A
【分析】根据题意可得AD = AB = 2, ∠B = ∠ADB, CE= DE, ∠C=∠CDE,可得∠ADE = 90°,继而设AE=x,则CE=DE=3-x,根据勾股定理即可求解.
解:∵沿过点A的直线将纸片折叠,使点B落在边BC上的点D处,
∴AD = AB = 2, ∠B = ∠ADB,
∵折叠纸片,使点C与点D重合,
∴CE= DE, ∠C=∠CDE,
∵∠BAC = 90°,
∴∠B+ ∠C= 90°,
∴∠ADB + ∠CDE = 90°,
∴∠ADE = 90°,
∴AD2 + DE2 = AE2,
设AE=x,则CE=DE=3-x,
∴22+(3-x)2 =x2,
解得
即AE=
故选A
二、填空题
11.5
【分析】首先证明,,设,在中,利用勾股定理构建方程即可解决问题.
解:如图,过点D作的垂线,垂足为P,
在中,∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
∴,,
设,
在中,∵,,
∴,
∴,
∴.
故答案为:5.
12.4
【分析】根据等腰三角形的性质和勾股定理求解即可.
解:∵在中,,是边的中线,
∴,,
在中,,,
∴,
故答案为:4.
13.
【分析】过H作于Q,再根据角平分线的性质和勾股定理列方程求解.
解:设,
过H作于Q,
在矩形中,,
∴,
由作图得:平分,
∴,
∵,,
∴,
∴,
∴,
在中,有,
即:,
解得:,
故答案为:.
14.
【分析】先建立直角三角形,利用勾股定理解决实际问题.
解:如图过点A、B分别作墙的垂线,交于点C,
则,,
在中,,
即
∵这台扫地机能从角落自由进出,
∴这台扫地机的直径不小于长,
即最小时为,
解得:(舍),,
∴图中的x至少为,
故答案为:.
15.
【分析】根据线段的垂直平分线和角平分线的作法可知:EF是线段AB的垂直平分线,AO是∠AOB的平分线,利用线段的垂直平分线的性质和角平分线的性质的求解即可.
解:如图所示:
根据题意可知:EF是线段AB的垂直平分线,AO是∠BAC的平分线,
∵AB=6,∠BAC=60°,
∴∠BAO=∠CAO=∠BAC=30°,AD=AB=3,
∴AM=2MD,
在Rt△ADM中,,
即,
∴MD=,
∵AM是∠AOB的平分线,MD⊥AB,
∴点M到射线AC的距离为.
故答案为:.
16.
【分析】利用勾股定理求出AC,再利用线段的垂直平分线的性质求出AD.
解:在Rt△ABC中,∠B=90°,AB=4,BC=8,
∴AC===4,
由作图可知,PQ垂直平分线段AC,
∴AD=DC=AC=2,
故答案为:2.
17.m2+1
【分析】2m为偶数,设其股是a,则弦为a+2,根据勾股定理列方程即可得到结论.
解:∵2m为偶数,
∴设其股是a,则弦为a+2,
根据勾股定理得,(2m)2+a2=(a+2)2,
解得a=m2-1,
∴弦长为m2+1,
故答案为:m2+1.
18.127
【分析】由已知图形观察规律,即可得到第六代勾股树中正方形的个数.
解:∵第一代勾股树中正方形有1+2=3(个),
第二代勾股树中正方形有1+2+22=7(个),
第三代勾股树中正方形有1+2+22+23=15(个),
......
∴第六代勾股树中正方形有1+2+22+23+24+25+26=127(个),
故答案为:127.
三、解答题
19.
(1)解:如图所示,即为所求;
(2)解:如图所示,,即为所求;
.
20.
解:(1)证明:,,
,
在和中,
,
;
(2)解:,
,
在中,,
,
.
21.
解:由题意得大正方形面积,小正方形面积,
4个小直角三角形的面积,
∵大正方形的面积=小正方形的面积+4个直角三角形的面积,
∴.
22.
解:(1)证明:∵ ADE是等腰直角三角形,
,
,
,
在与中
;
,
(2)在中,,,
,
,
,
,
,
∴∠ADC=∠ACD,
,
.
23.
解:(1)在Rt△ABC中,;
(2)∵,
∴,
∴,
∵在Rt△ABC中,,
∴
∴,
∴,∴.
综上所述,长度增加了2米.
