8.3 实数及其简单运算 课件(共14张PPT)
文档属性
| 名称 | 8.3 实数及其简单运算 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 19:12:31 | ||
图片预览






文档简介
(共14张PPT)
第八章 实数
8.3 实数及其简单的运算(第一课时)
认清目标,扬帆起航
1、理解无理数和实数的概念,会对实数进行分类,发展抽象能力).
2.了解实数与数轴上点的一一对应关系,体会实数的连续性,发展几何直观.
3.类比有理数学习实数,进一步体会数系扩充思想.
重点:引人无理数,把数系扩充到实数.
难点:理解无理数的特征.
在前面的学习中,我们通过引人一类新的数——负数,使数的范围扩充到有理数,本章我们认识了像 这样的无限不循环小数,它们是有理数吗?如果不是,我们将再次扩充数的范围.
一、复习引入,提出问题
一、复习引入,提出问题
下列各数是有理数吗 你能将这些数写成小数的形式吗 你有什么发现
追问:反过来,你能把0.5,0.72,0.3转化为分数吗?
有理数都可以写成有限小数或无限循环小数;
反过来,任何有限小数和无限循环小数都是有理数.
一、复习引入,提出问题
前面学习中除了上述类型的小数,还有什么小数?你能举例吗?
通过前两节的学习,我们知道,很多数的平方根、立方根是无限不循环小数,例如 等.
π=3.14159265···也是无限不循环小数.
从上面的讨论可知,无限不循环小数都不是有理数无限不循环小数又叫作无理数.
有理数和无理数统称实数.
二、类比思考,研究思路
我们是怎样研究有理数的 你认为应该怎样研究实数
引入新数——定义、表示、分类——大小比较——运算.
三、分类表示,连续性
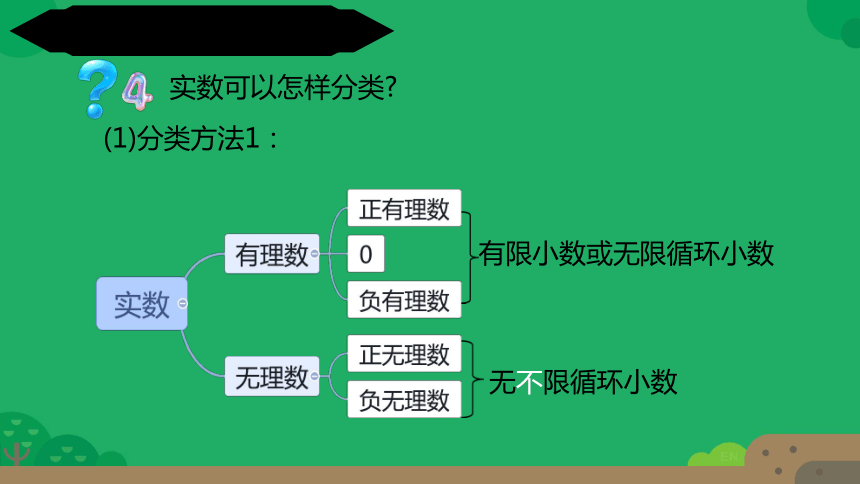
实数可以怎样分类
(1)分类方法1:
有限小数或无限循环小数
无不限循环小数
三、分类表示,连续性
实数可以怎样分类
(2)分类方法2:
追问1:如图,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点由原点到达点O',则点O'对应的数是多少
四、类比思考,新知形成
与有理数可以用数轴上的点表示类似,无理数也可以用数轴上的点表示.如何表示呢?
追问2:如图,以1个单位长度为边长画一个正方形,以原点为圆心,以正方形的对角线为半经画弧,与数轴正半轴的交点A表示什么数?与数轴负半轴的交点B表示什么数?
四、类比思考,新知形成
当数的范围从有理数扩充到实数以后,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数,因此,实数与数轴上的点是一一对应的.
四、类比思考,新知形成
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
五、辨别应用,巩固新知
2.把下列各数填在相应的大括号内:
0,
-2,
0.515515551…….
自然数集合{ ……}
有理数集合{ ……}
无理数集合{ ……}
正数集合{ ……}
整数集合{ ……}
分数集合{ ……}
非负整数集合{ ……}
五、辨别应用,巩固新知
1.有理数和无理数的特点是什么?举例说明,
2.把数的范围从有理数扩充到实数后,数轴上表示数的点加密到什么程度?
3.实数与数轴上的点有什么关系?
4.类比有理数的学习,你认为接下来要学习什么?
六、课堂小结,发展能力
第八章 实数
8.3 实数及其简单的运算(第一课时)
认清目标,扬帆起航
1、理解无理数和实数的概念,会对实数进行分类,发展抽象能力).
2.了解实数与数轴上点的一一对应关系,体会实数的连续性,发展几何直观.
3.类比有理数学习实数,进一步体会数系扩充思想.
重点:引人无理数,把数系扩充到实数.
难点:理解无理数的特征.
在前面的学习中,我们通过引人一类新的数——负数,使数的范围扩充到有理数,本章我们认识了像 这样的无限不循环小数,它们是有理数吗?如果不是,我们将再次扩充数的范围.
一、复习引入,提出问题
一、复习引入,提出问题
下列各数是有理数吗 你能将这些数写成小数的形式吗 你有什么发现
追问:反过来,你能把0.5,0.72,0.3转化为分数吗?
有理数都可以写成有限小数或无限循环小数;
反过来,任何有限小数和无限循环小数都是有理数.
一、复习引入,提出问题
前面学习中除了上述类型的小数,还有什么小数?你能举例吗?
通过前两节的学习,我们知道,很多数的平方根、立方根是无限不循环小数,例如 等.
π=3.14159265···也是无限不循环小数.
从上面的讨论可知,无限不循环小数都不是有理数无限不循环小数又叫作无理数.
有理数和无理数统称实数.
二、类比思考,研究思路
我们是怎样研究有理数的 你认为应该怎样研究实数
引入新数——定义、表示、分类——大小比较——运算.
三、分类表示,连续性
实数可以怎样分类
(1)分类方法1:
有限小数或无限循环小数
无不限循环小数
三、分类表示,连续性
实数可以怎样分类
(2)分类方法2:
追问1:如图,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点由原点到达点O',则点O'对应的数是多少
四、类比思考,新知形成
与有理数可以用数轴上的点表示类似,无理数也可以用数轴上的点表示.如何表示呢?
追问2:如图,以1个单位长度为边长画一个正方形,以原点为圆心,以正方形的对角线为半经画弧,与数轴正半轴的交点A表示什么数?与数轴负半轴的交点B表示什么数?
四、类比思考,新知形成
当数的范围从有理数扩充到实数以后,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数,因此,实数与数轴上的点是一一对应的.
四、类比思考,新知形成
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
五、辨别应用,巩固新知
2.把下列各数填在相应的大括号内:
0,
-2,
0.515515551…….
自然数集合{ ……}
有理数集合{ ……}
无理数集合{ ……}
正数集合{ ……}
整数集合{ ……}
分数集合{ ……}
非负整数集合{ ……}
五、辨别应用,巩固新知
1.有理数和无理数的特点是什么?举例说明,
2.把数的范围从有理数扩充到实数后,数轴上表示数的点加密到什么程度?
3.实数与数轴上的点有什么关系?
4.类比有理数的学习,你认为接下来要学习什么?
六、课堂小结,发展能力
同课章节目录
