人教版 六年级下册数学 第四单元《比例》试卷(含答案)
文档属性
| 名称 | 人教版 六年级下册数学 第四单元《比例》试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 12:38:10 | ||
图片预览



文档简介
人教版六下数学第四单元《比例》试卷
题序 一 二 三 四 五 综合评价
自我评价
一、精心选择。(每空1分,共13分)
1.下面各式中,( )是比例。
A. 4∶2=2 B. 3×4=2×6 C. 20= D. =
2.下面不能组成比例的是( )。
A.7∶8和14∶16 B.0.6∶2和0.3∶1 C.∶和2∶3 D.3∶8和0.2∶0.6
3.比例尺 表示( )。
A.图上距离是实际距离的 B.实际距离与图上距离的比是1∶600000
C.实际距离是图上距离的600000倍 D.图上距离与实际距离的比是1∶6
4.一张图纸的比例尺是40∶1,在这张图纸上画的最有可能是( )。
A.一本书 B.一间教室 C.手机零件 D.一棵大树
5.已知x和y成反比例关系,当x=2时,y=;当x=5时,y=( )。
A. B. C. 2 D.
6.如图,三角形a边上的高为b,c边上的高为d。根据这些信息,下面式子不成立的是( )。
A. a∶c=d∶b B.a∶c=b∶d
C. = D. =
7有两个相关联的量,它们的关系可以用下图表示,这两个量可能是( )。
A.面积是12平方米时,平行四边形的底和高
B.正方体的体积和它的棱长
C.乐乐看《数学故事》,已看的页数和未看的页数
D.一辆自行车匀速行驶,行驶的时间与所行的路程
8.在15∶6=5∶2中,如果内项6加上9,要使比例仍然成立,外项2应该( D )。
A.加上9 B.加上13 C.乘1.5 D.乘2.5
9.同学们搜索了厦门市现在的地铁线网图进行了手机截图,供课后实践使用。下面图1是小华按照1∶a的比例尺呈现的该截图,图2是小丽呈现的该截图,小丽使用的比例尺是( )。
图1 图2
A.1∶a B.1∶a C.a∶1 D.1∶2a
钩码质量/g 0 50 150 250 ……
弹簧长度/cm 10 10.5 11.5 12.5 ……
10.优优在弹簧测力计上分别挂上不同质量的钩码,观察弹簧长度变化的情况,实验数据如下表所示。
(1)分析表中数据可知,弹簧被拉长的长度和钩码质量的关系是( )。
A.成正比例 B.成反比例 C.不成比例
(2)当钩码质量为350g时,弹簧的长度是( )cm。
A.3.5 B.13 C.13.5 D.23.5
11.将一个周长是12cm的正方形放大成一个面积是36cm2的正方形,是按( )放大的。
A.1∶3 B.2∶1 C.3∶1 D.4∶1
12.在大型文艺汇演中,同学们每行站20人,正好站18行。如果每行站24人,那么可以站多少行?若设可以站x行,则下面列出的方程或比例正确的有( )。
①= ②24x=20×18 ③x∶24=20∶18 ④20∶24=x∶18
A.①② B.②④ C.③④ D.①④
二、用心填写。(第5题5分,其余每空1分,共13分)
1.在一个比例中,如果两个外项的积是28.8,一个内项是0.4,那么另一个内项是( )。
2.从36的因数中选出四个数,组成一个比例是( )。
3.把3a=b(a, b均不为0)或写成比例是a∶b=( )∶( )。(填最简单的整数比)
4.如果=(x、y均不为0),那么当k一定时,x和y成( )比例关系。
5.( 说理表达)由我国完全自主设计建造的第一艘弹射型航空母舰福建舰的长度是320米。(1)聪聪平时喜欢研究各种军舰,爸爸给他买了一个长度是20厘米的福建舰模型,这个模型是按照( )的比缩小的。
(2)聪聪还收集了一张福建舰的纪念卡片,他想要得到按2∶1的比扩大的复印件一份,家中的复印机只有三种功能: (按 功能复印一次,就是将原图按1∶2缩小)。聪聪至少复印( )次才能实现。
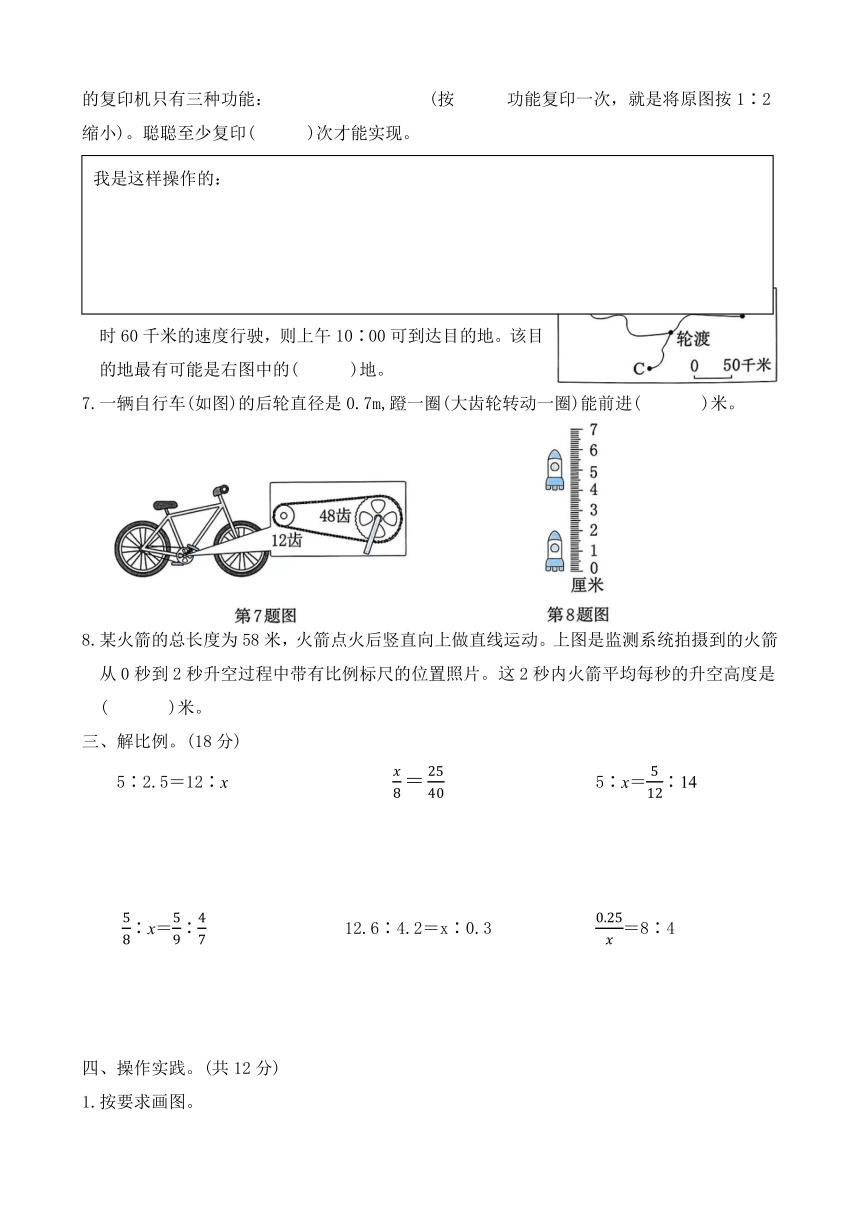
6.王叔叔上午8∶00驾车从轮渡出发去某地游玩,如果以每 小时60千米的速度行驶,则上午10∶00可到达目的地。该目的地最有可能是右图中的( )地。
7.一辆自行车(如图)的后轮直径是0.7m,蹬一圈(大齿轮转动一圈)能前进( )米。
8.某火箭的总长度为58米,火箭点火后竖直向上做直线运动。上图是监测系统拍摄到的火箭从0秒到2秒升空过程中带有比例标尺的位置照片。这2秒内火箭平均每秒的升空高度是( )米。
三、解比例。(18分)
5∶2.5=12∶x 5∶x=∶14
∶x=∶ 12.6∶4.2=x∶0.3 =8∶4
四、操作实践。(共12分)
1.按要求画图。
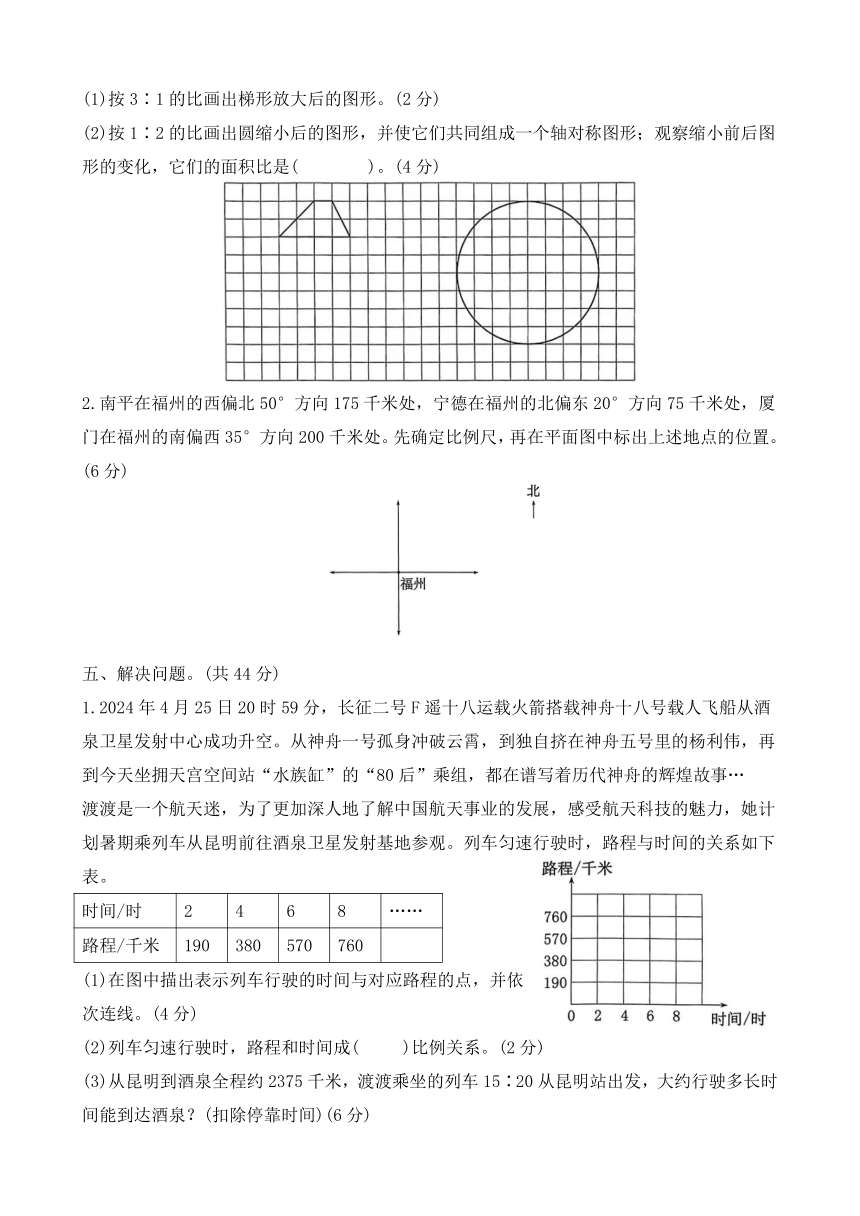
(1)按3∶1的比画出梯形放大后的图形。(2分)
(2)按1∶2的比画出圆缩小后的图形,并使它们共同组成一个轴对称图形;观察缩小前后图形的变化,它们的面积比是( )。(4分)
2.南平在福州的西偏北50°方向175千米处,宁德在福州的北偏东20°方向75千米处,厦门在福州的南偏西35°方向200千米处。先确定比例尺,再在平面图中标出上述地点的位置。(6分)
五、解决问题。(共44分)
1.2024年4月25日20时59分,长征二号F遥十八运载火箭搭载神舟十八号载人飞船从酒泉卫星发射中心成功升空。从神舟一号孤身冲破云霄,到独自挤在神舟五号里的杨利伟,再到今天坐拥天宫空间站“水族缸”的“80后”乘组,都在谱写着历代神舟的辉煌故事…
渡渡是一个航天迷,为了更加深人地了解中国航天事业的发展,感受航天科技的魅力,她计划暑期乘列车从昆明前往酒泉卫星发射基地参观。列车匀速行驶时,路程与时间的关系如下表。
时间/时 2 4 6 8 ……
路程/千米 190 380 570 760
(1)在图中描出表示列车行驶的时间与对应路程的点,并依次连线。(4分)
(2)列车匀速行驶时,路程和时间成( )比例关系。(2分)
(3)从昆明到酒泉全程约2375千米,渡渡乘坐的列车15∶20从昆明站出发,大约行驶多长时间能到达酒泉?(扣除停靠时间)(6分)
(4)在一幅比例尺为1:5000000的地图上,昆明到酒泉的图上距离约是多少厘米?(6分)
2.聪聪一家去厦门旅游,在鼓浪屿的东南角有一座巍峨的郑成功巨型雕像,雄威凛然,矗立在覆鼎岩之巅。聪聪问爸爸:“这座雕像有多高?”爸爸灵机一动,让聪聪和妈妈站在雕像旁拍了一张合照,洗出照片后量得照片中聪聪的高度为3cm,雕像的高度为31.4cm。
(1)已知聪聪的身高是1.5m,现在你能告诉聪聪这座雕像高多少米吗?(6分)
(2)妈妈的真实身高是1.65m,妈妈在照片中的高度为多少?(6分)
3.请你选择一个问题,把序号填在横线上,并用比例知识解答。(6分)
服装厂赶制一批衣服,原计划每天生产240件,22天能完成任务,照这样计算, ?
①机器升级,如果每天生产320件,需要几天完成?
②如果需要提前2天完成,每天需要生产多少件?
4.为了研究二维码中的数学问题,亮亮和聪聪做了一个数学实验,操作步骤如下:
①亮亮测量了一个二维码的四条边,发现这是一个边长为2.5厘米的正方形;
②为了方便做实验,聪聪将这个二维码按20∶1放大后打印出来;
③亮亮准备了一些围棋棋子,随机扔进放大后的二维码内,他一共实验了875次,棋子落入黑色区域525次。(落人黑色区域的次数占实验总次数的几分之几就大约表示黑色区域的面积占二维码面积的几分之几)
根据上面的信息计算一下,放大后的二维码中黑色区域的面积大约是多少平方厘米?(8分)
人教版六下数学第四单元《比例》试卷
题序 一 二 三 四 五 综合评价
自我评价
一、精心选择。(每空1分,共13分)
1.下面各式中,( D )是比例。
A. 4∶2=2 B. 3×4=2×6 C. 20= D. =
2.下面不能组成比例的是( D )。
A.7∶8和14∶16 B.0.6∶2和0.3∶1 C.∶和2∶3 D.3∶8和0.2∶0.6
3.比例尺 表示( C )。
A.图上距离是实际距离的 B.实际距离与图上距离的比是1∶600000
C.实际距离是图上距离的600000倍 D.图上距离与实际距离的比是1∶6
4.一张图纸的比例尺是40∶1,在这张图纸上画的最有可能是( C )。
A.一本书 B.一间教室 C.手机零件 D.一棵大树
5.已知x和y成反比例关系,当x=2时,y=;当x=5时,y=( A )。
A. B. C. 2 D.
6.如图,三角形a边上的高为b,c边上的高为d。根据这些信息,下面式子不成立的是( B )。
A. a∶c=d∶b B.a∶c=b∶d
C. = D. =
7有两个相关联的量,它们的关系可以用下图表示,这两个量可能是( D )。
A.面积是12平方米时,平行四边形的底和高
B.正方体的体积和它的棱长
C.乐乐看《数学故事》,已看的页数和未看的页数
D.一辆自行车匀速行驶,行驶的时间与所行的路程
8.在15∶6=5∶2中,如果内项6加上9,要使比例仍然成立,外项2应该( D )。
A.加上9 B.加上13 C.乘1.5 D.乘2.5
9.同学们搜索了厦门市现在的地铁线网图进行了手机截图,供课后实践使用。下面图1是小华按照1∶a的比例尺呈现的该截图,图2是小丽呈现的该截图,小丽使用的比例尺是( D )。
图1 图2
A.1∶a B.1∶a C.a∶1 D.1∶2a
钩码质量/g 0 50 150 250 ……
弹簧长度/cm 10 10.5 11.5 12.5 ……
10.优优在弹簧测力计上分别挂上不同质量的钩码,观察弹簧长度变化的情况,实验数据如下表所示。
(1)分析表中数据可知,弹簧被拉长的长度和钩码质量的关系是( A )。
A.成正比例 B.成反比例 C.不成比例
(2)当钩码质量为350g时,弹簧的长度是( C )cm。
A.3.5 B.13 C.13.5 D.23.5
11.将一个周长是12cm的正方形放大成一个面积是36cm2的正方形,是按( B )放大的。
A.1∶3 B.2∶1 C.3∶1 D.4∶1
12.在大型文艺汇演中,同学们每行站20人,正好站18行。如果每行站24人,那么可以站多少行?若设可以站x行,则下面列出的方程或比例正确的有( B )。
①= ②24x=20×18 ③x∶24=20∶18 ④20∶24=x∶18
A.①② B.②④ C.③④ D.①④
二、用心填写。(第5题5分,其余每空1分,共13分)
1.在一个比例中,如果两个外项的积是28.8,一个内项是0.4,那么另一个内项是( 72 )。
2.从36的因数中选出四个数,组成一个比例是( 12∶4=9∶3 )。
3.把3a=b(a, b均不为0)或写成比例是a∶b=( 1 )∶( 4 )。(填最简单的整数比)
4.如果=(x、y均不为0),那么当k一定时,x和y成( 正 )比例关系。
5.(说理表达)由我国完全自主设计建造的第一艘弹射型航空母舰福建舰的长度是320米。(1)聪聪平时喜欢研究各种军舰,爸爸给他买了一个长度是20厘米的福建舰模型,这个模型是按照( 1∶1600 )的比缩小的。
(2)聪聪还收集了一张福建舰的纪念卡片,他想要得到按2∶1的比扩大的复印件一份,家中的复印机只有三种功能: (按 功能复印一次,就是将原图按1∶2缩小)。聪聪至少复印( 3 )次才能实现。
6.王叔叔上午8∶00驾车从轮渡出发去某地游玩,如果以每 小时60千米的速度行驶,则上午10∶00可到达目的地。该目的地最有可能是右图中的( B )地。
7.一辆自行车(如图)的后轮直径是0.7m,蹬一圈(大齿轮转动一圈)能前进( 8.792 )米。
8.某火箭的总长度为58米,火箭点火后竖直向上做直线运动。上图是监测系统拍摄到的火箭从0秒到2秒升空过程中带有比例标尺的位置照片。这2秒内火箭平均每秒的升空高度是( 58 )米。
三、解比例。(18分)
5∶2.5=12∶x 5∶x=∶14
x=6 x=5 x=168
∶x=∶ 12.6∶4.2=x∶0.3 =8∶4
x= x=0.9 x=
四、操作实践。(共12分)
1.按要求画图。
(1)按3∶1的比画出梯形放大后的图形。(2分)
(2)按1∶2的比画出圆缩小后的图形,并使它们共同组成一个轴对称图形;观察缩小前后图形的变化,它们的面积比是( 1∶4 答案不唯一 )。(4分)
2.南平在福州的西偏北50°方向175千米处,宁德在福州的北偏东20°方向75千米处,厦门在福州的南偏西35°方向200千米处。先确定比例尺,再在平面图中标出上述地点的位置。(6分)
五、解决问题。(共44分)
1.2024年4月25日20时59分,长征二号F遥十八运载火箭搭载神舟十八号载人飞船从酒泉卫星发射中心成功升空。从神舟一号孤身冲破云霄,到独自挤在神舟五号里的杨利伟,再到今天坐拥天宫空间站“水族缸”的“80后”乘组,都在谱写着历代神舟的辉煌故事…
渡渡是一个航天迷,为了更加深人地了解中国航天事业的发展,感受航天科技的魅力,她计划暑期乘列车从昆明前往酒泉卫星发射基地参观。列车匀速行驶时,路程与时间的关系如下表。
时间/时 2 4 6 8 ……
路程/千米 190 380 570 760
(1)在图中描出表示列车行驶的时间与对应路程的点,并依次连线。(4分)
(2)列车匀速行驶时,路程和时间成( 正 )比例关系。(2分)
(3)从昆明到酒泉全程约2375千米,渡渡乘坐的列车15∶20从昆明站出发,大约行驶多长时间能到达酒泉?(扣除停靠时间)(6分)
解:设大约行驶x小时能到达酒泉。
190∶2=2375∶x
x=25
答:大约行驶25小时能到达酒泉。
(4)在一幅比例尺为1:5000000的地图上,昆明到酒泉的图上距离约是多少厘米?(6分)
2375千米=237500000厘米
237500000×=47.5(厘米)
答:昆明到酒泉的图上距离约是47.5厘米。
2.聪聪一家去厦门旅游,在鼓浪屿的东南角有一座巍峨的郑成功巨型雕像,雄威凛然,矗立在覆鼎岩之巅。聪聪问爸爸:“这座雕像有多高?”爸爸灵机一动,让聪聪和妈妈站在雕像旁拍了一张合照,洗出照片后量得照片中聪聪的高度为3cm,雕像的高度为31.4cm。
(1)已知聪聪的身高是1.5m,现在你能告诉聪聪这座雕像高多少米吗?(6分)
1.5m=150cm
解:设这座雕像高x m。
3∶150=31.4∶x
x=1570
1570cm=15.7m
答:这座雕像高15.7m。
(2)妈妈的真实身高是1.65m,妈妈在照片中的高度为多少?(6分)
1.65m=165cm
解:设妈妈在照片中的高度为xcm。
3∶150= x∶165
x=3.3
答:妈妈在照片中的高度为3.3cm。
3.请你选择一个问题,把序号填在横线上,并用比例知识解答。(6分)
服装厂赶制一批衣服,原计划每天生产240件,22天能完成任务,照这样计算, ?
①机器升级,如果每天生产320件,需要几天完成?
②如果需要提前2天完成,每天需要生产多少件?
若选①
解:设需要x天完成。
320 x=240×22
x=16.5
答:需要16.5天完成。
若选②
解:设每天需要生产y件。
240×22=(22-2) y
y=264
答:每天需要生产264件。
4.为了研究二维码中的数学问题,亮亮和聪聪做了一个数学实验,操作步骤如下:
①亮亮测量了一个二维码的四条边,发现这是一个边长为2.5厘米的正方形;
②为了方便做实验,聪聪将这个二维码按20∶1放大后打印出来;
③亮亮准备了一些围棋棋子,随机扔进放大后的二维码内,他一共实验了875次,棋子落入黑色区域525次。(落人黑色区域的次数占实验总次数的几分之几就大约表示黑色区域的面积占二维码面积的几分之几)
根据上面的信息计算一下,放大后的二维码中黑色区域的面积大约是多少平方厘米?(8分)
2.5×2.5×20×20=2500(平方厘米)
2500×=1500(平方厘米)
答:放大后的二维码中黑色区域的面积大约是1500平方厘米。
题序 一 二 三 四 五 综合评价
自我评价
一、精心选择。(每空1分,共13分)
1.下面各式中,( )是比例。
A. 4∶2=2 B. 3×4=2×6 C. 20= D. =
2.下面不能组成比例的是( )。
A.7∶8和14∶16 B.0.6∶2和0.3∶1 C.∶和2∶3 D.3∶8和0.2∶0.6
3.比例尺 表示( )。
A.图上距离是实际距离的 B.实际距离与图上距离的比是1∶600000
C.实际距离是图上距离的600000倍 D.图上距离与实际距离的比是1∶6
4.一张图纸的比例尺是40∶1,在这张图纸上画的最有可能是( )。
A.一本书 B.一间教室 C.手机零件 D.一棵大树
5.已知x和y成反比例关系,当x=2时,y=;当x=5时,y=( )。
A. B. C. 2 D.
6.如图,三角形a边上的高为b,c边上的高为d。根据这些信息,下面式子不成立的是( )。
A. a∶c=d∶b B.a∶c=b∶d
C. = D. =
7有两个相关联的量,它们的关系可以用下图表示,这两个量可能是( )。
A.面积是12平方米时,平行四边形的底和高
B.正方体的体积和它的棱长
C.乐乐看《数学故事》,已看的页数和未看的页数
D.一辆自行车匀速行驶,行驶的时间与所行的路程
8.在15∶6=5∶2中,如果内项6加上9,要使比例仍然成立,外项2应该( D )。
A.加上9 B.加上13 C.乘1.5 D.乘2.5
9.同学们搜索了厦门市现在的地铁线网图进行了手机截图,供课后实践使用。下面图1是小华按照1∶a的比例尺呈现的该截图,图2是小丽呈现的该截图,小丽使用的比例尺是( )。
图1 图2
A.1∶a B.1∶a C.a∶1 D.1∶2a
钩码质量/g 0 50 150 250 ……
弹簧长度/cm 10 10.5 11.5 12.5 ……
10.优优在弹簧测力计上分别挂上不同质量的钩码,观察弹簧长度变化的情况,实验数据如下表所示。
(1)分析表中数据可知,弹簧被拉长的长度和钩码质量的关系是( )。
A.成正比例 B.成反比例 C.不成比例
(2)当钩码质量为350g时,弹簧的长度是( )cm。
A.3.5 B.13 C.13.5 D.23.5
11.将一个周长是12cm的正方形放大成一个面积是36cm2的正方形,是按( )放大的。
A.1∶3 B.2∶1 C.3∶1 D.4∶1
12.在大型文艺汇演中,同学们每行站20人,正好站18行。如果每行站24人,那么可以站多少行?若设可以站x行,则下面列出的方程或比例正确的有( )。
①= ②24x=20×18 ③x∶24=20∶18 ④20∶24=x∶18
A.①② B.②④ C.③④ D.①④
二、用心填写。(第5题5分,其余每空1分,共13分)
1.在一个比例中,如果两个外项的积是28.8,一个内项是0.4,那么另一个内项是( )。
2.从36的因数中选出四个数,组成一个比例是( )。
3.把3a=b(a, b均不为0)或写成比例是a∶b=( )∶( )。(填最简单的整数比)
4.如果=(x、y均不为0),那么当k一定时,x和y成( )比例关系。
5.( 说理表达)由我国完全自主设计建造的第一艘弹射型航空母舰福建舰的长度是320米。(1)聪聪平时喜欢研究各种军舰,爸爸给他买了一个长度是20厘米的福建舰模型,这个模型是按照( )的比缩小的。
(2)聪聪还收集了一张福建舰的纪念卡片,他想要得到按2∶1的比扩大的复印件一份,家中的复印机只有三种功能: (按 功能复印一次,就是将原图按1∶2缩小)。聪聪至少复印( )次才能实现。
6.王叔叔上午8∶00驾车从轮渡出发去某地游玩,如果以每 小时60千米的速度行驶,则上午10∶00可到达目的地。该目的地最有可能是右图中的( )地。
7.一辆自行车(如图)的后轮直径是0.7m,蹬一圈(大齿轮转动一圈)能前进( )米。
8.某火箭的总长度为58米,火箭点火后竖直向上做直线运动。上图是监测系统拍摄到的火箭从0秒到2秒升空过程中带有比例标尺的位置照片。这2秒内火箭平均每秒的升空高度是( )米。
三、解比例。(18分)
5∶2.5=12∶x 5∶x=∶14
∶x=∶ 12.6∶4.2=x∶0.3 =8∶4
四、操作实践。(共12分)
1.按要求画图。
(1)按3∶1的比画出梯形放大后的图形。(2分)
(2)按1∶2的比画出圆缩小后的图形,并使它们共同组成一个轴对称图形;观察缩小前后图形的变化,它们的面积比是( )。(4分)
2.南平在福州的西偏北50°方向175千米处,宁德在福州的北偏东20°方向75千米处,厦门在福州的南偏西35°方向200千米处。先确定比例尺,再在平面图中标出上述地点的位置。(6分)
五、解决问题。(共44分)
1.2024年4月25日20时59分,长征二号F遥十八运载火箭搭载神舟十八号载人飞船从酒泉卫星发射中心成功升空。从神舟一号孤身冲破云霄,到独自挤在神舟五号里的杨利伟,再到今天坐拥天宫空间站“水族缸”的“80后”乘组,都在谱写着历代神舟的辉煌故事…
渡渡是一个航天迷,为了更加深人地了解中国航天事业的发展,感受航天科技的魅力,她计划暑期乘列车从昆明前往酒泉卫星发射基地参观。列车匀速行驶时,路程与时间的关系如下表。
时间/时 2 4 6 8 ……
路程/千米 190 380 570 760
(1)在图中描出表示列车行驶的时间与对应路程的点,并依次连线。(4分)
(2)列车匀速行驶时,路程和时间成( )比例关系。(2分)
(3)从昆明到酒泉全程约2375千米,渡渡乘坐的列车15∶20从昆明站出发,大约行驶多长时间能到达酒泉?(扣除停靠时间)(6分)
(4)在一幅比例尺为1:5000000的地图上,昆明到酒泉的图上距离约是多少厘米?(6分)
2.聪聪一家去厦门旅游,在鼓浪屿的东南角有一座巍峨的郑成功巨型雕像,雄威凛然,矗立在覆鼎岩之巅。聪聪问爸爸:“这座雕像有多高?”爸爸灵机一动,让聪聪和妈妈站在雕像旁拍了一张合照,洗出照片后量得照片中聪聪的高度为3cm,雕像的高度为31.4cm。
(1)已知聪聪的身高是1.5m,现在你能告诉聪聪这座雕像高多少米吗?(6分)
(2)妈妈的真实身高是1.65m,妈妈在照片中的高度为多少?(6分)
3.请你选择一个问题,把序号填在横线上,并用比例知识解答。(6分)
服装厂赶制一批衣服,原计划每天生产240件,22天能完成任务,照这样计算, ?
①机器升级,如果每天生产320件,需要几天完成?
②如果需要提前2天完成,每天需要生产多少件?
4.为了研究二维码中的数学问题,亮亮和聪聪做了一个数学实验,操作步骤如下:
①亮亮测量了一个二维码的四条边,发现这是一个边长为2.5厘米的正方形;
②为了方便做实验,聪聪将这个二维码按20∶1放大后打印出来;
③亮亮准备了一些围棋棋子,随机扔进放大后的二维码内,他一共实验了875次,棋子落入黑色区域525次。(落人黑色区域的次数占实验总次数的几分之几就大约表示黑色区域的面积占二维码面积的几分之几)
根据上面的信息计算一下,放大后的二维码中黑色区域的面积大约是多少平方厘米?(8分)
人教版六下数学第四单元《比例》试卷
题序 一 二 三 四 五 综合评价
自我评价
一、精心选择。(每空1分,共13分)
1.下面各式中,( D )是比例。
A. 4∶2=2 B. 3×4=2×6 C. 20= D. =
2.下面不能组成比例的是( D )。
A.7∶8和14∶16 B.0.6∶2和0.3∶1 C.∶和2∶3 D.3∶8和0.2∶0.6
3.比例尺 表示( C )。
A.图上距离是实际距离的 B.实际距离与图上距离的比是1∶600000
C.实际距离是图上距离的600000倍 D.图上距离与实际距离的比是1∶6
4.一张图纸的比例尺是40∶1,在这张图纸上画的最有可能是( C )。
A.一本书 B.一间教室 C.手机零件 D.一棵大树
5.已知x和y成反比例关系,当x=2时,y=;当x=5时,y=( A )。
A. B. C. 2 D.
6.如图,三角形a边上的高为b,c边上的高为d。根据这些信息,下面式子不成立的是( B )。
A. a∶c=d∶b B.a∶c=b∶d
C. = D. =
7有两个相关联的量,它们的关系可以用下图表示,这两个量可能是( D )。
A.面积是12平方米时,平行四边形的底和高
B.正方体的体积和它的棱长
C.乐乐看《数学故事》,已看的页数和未看的页数
D.一辆自行车匀速行驶,行驶的时间与所行的路程
8.在15∶6=5∶2中,如果内项6加上9,要使比例仍然成立,外项2应该( D )。
A.加上9 B.加上13 C.乘1.5 D.乘2.5
9.同学们搜索了厦门市现在的地铁线网图进行了手机截图,供课后实践使用。下面图1是小华按照1∶a的比例尺呈现的该截图,图2是小丽呈现的该截图,小丽使用的比例尺是( D )。
图1 图2
A.1∶a B.1∶a C.a∶1 D.1∶2a
钩码质量/g 0 50 150 250 ……
弹簧长度/cm 10 10.5 11.5 12.5 ……
10.优优在弹簧测力计上分别挂上不同质量的钩码,观察弹簧长度变化的情况,实验数据如下表所示。
(1)分析表中数据可知,弹簧被拉长的长度和钩码质量的关系是( A )。
A.成正比例 B.成反比例 C.不成比例
(2)当钩码质量为350g时,弹簧的长度是( C )cm。
A.3.5 B.13 C.13.5 D.23.5
11.将一个周长是12cm的正方形放大成一个面积是36cm2的正方形,是按( B )放大的。
A.1∶3 B.2∶1 C.3∶1 D.4∶1
12.在大型文艺汇演中,同学们每行站20人,正好站18行。如果每行站24人,那么可以站多少行?若设可以站x行,则下面列出的方程或比例正确的有( B )。
①= ②24x=20×18 ③x∶24=20∶18 ④20∶24=x∶18
A.①② B.②④ C.③④ D.①④
二、用心填写。(第5题5分,其余每空1分,共13分)
1.在一个比例中,如果两个外项的积是28.8,一个内项是0.4,那么另一个内项是( 72 )。
2.从36的因数中选出四个数,组成一个比例是( 12∶4=9∶3 )。
3.把3a=b(a, b均不为0)或写成比例是a∶b=( 1 )∶( 4 )。(填最简单的整数比)
4.如果=(x、y均不为0),那么当k一定时,x和y成( 正 )比例关系。
5.(说理表达)由我国完全自主设计建造的第一艘弹射型航空母舰福建舰的长度是320米。(1)聪聪平时喜欢研究各种军舰,爸爸给他买了一个长度是20厘米的福建舰模型,这个模型是按照( 1∶1600 )的比缩小的。
(2)聪聪还收集了一张福建舰的纪念卡片,他想要得到按2∶1的比扩大的复印件一份,家中的复印机只有三种功能: (按 功能复印一次,就是将原图按1∶2缩小)。聪聪至少复印( 3 )次才能实现。
6.王叔叔上午8∶00驾车从轮渡出发去某地游玩,如果以每 小时60千米的速度行驶,则上午10∶00可到达目的地。该目的地最有可能是右图中的( B )地。
7.一辆自行车(如图)的后轮直径是0.7m,蹬一圈(大齿轮转动一圈)能前进( 8.792 )米。
8.某火箭的总长度为58米,火箭点火后竖直向上做直线运动。上图是监测系统拍摄到的火箭从0秒到2秒升空过程中带有比例标尺的位置照片。这2秒内火箭平均每秒的升空高度是( 58 )米。
三、解比例。(18分)
5∶2.5=12∶x 5∶x=∶14
x=6 x=5 x=168
∶x=∶ 12.6∶4.2=x∶0.3 =8∶4
x= x=0.9 x=
四、操作实践。(共12分)
1.按要求画图。
(1)按3∶1的比画出梯形放大后的图形。(2分)
(2)按1∶2的比画出圆缩小后的图形,并使它们共同组成一个轴对称图形;观察缩小前后图形的变化,它们的面积比是( 1∶4 答案不唯一 )。(4分)
2.南平在福州的西偏北50°方向175千米处,宁德在福州的北偏东20°方向75千米处,厦门在福州的南偏西35°方向200千米处。先确定比例尺,再在平面图中标出上述地点的位置。(6分)
五、解决问题。(共44分)
1.2024年4月25日20时59分,长征二号F遥十八运载火箭搭载神舟十八号载人飞船从酒泉卫星发射中心成功升空。从神舟一号孤身冲破云霄,到独自挤在神舟五号里的杨利伟,再到今天坐拥天宫空间站“水族缸”的“80后”乘组,都在谱写着历代神舟的辉煌故事…
渡渡是一个航天迷,为了更加深人地了解中国航天事业的发展,感受航天科技的魅力,她计划暑期乘列车从昆明前往酒泉卫星发射基地参观。列车匀速行驶时,路程与时间的关系如下表。
时间/时 2 4 6 8 ……
路程/千米 190 380 570 760
(1)在图中描出表示列车行驶的时间与对应路程的点,并依次连线。(4分)
(2)列车匀速行驶时,路程和时间成( 正 )比例关系。(2分)
(3)从昆明到酒泉全程约2375千米,渡渡乘坐的列车15∶20从昆明站出发,大约行驶多长时间能到达酒泉?(扣除停靠时间)(6分)
解:设大约行驶x小时能到达酒泉。
190∶2=2375∶x
x=25
答:大约行驶25小时能到达酒泉。
(4)在一幅比例尺为1:5000000的地图上,昆明到酒泉的图上距离约是多少厘米?(6分)
2375千米=237500000厘米
237500000×=47.5(厘米)
答:昆明到酒泉的图上距离约是47.5厘米。
2.聪聪一家去厦门旅游,在鼓浪屿的东南角有一座巍峨的郑成功巨型雕像,雄威凛然,矗立在覆鼎岩之巅。聪聪问爸爸:“这座雕像有多高?”爸爸灵机一动,让聪聪和妈妈站在雕像旁拍了一张合照,洗出照片后量得照片中聪聪的高度为3cm,雕像的高度为31.4cm。
(1)已知聪聪的身高是1.5m,现在你能告诉聪聪这座雕像高多少米吗?(6分)
1.5m=150cm
解:设这座雕像高x m。
3∶150=31.4∶x
x=1570
1570cm=15.7m
答:这座雕像高15.7m。
(2)妈妈的真实身高是1.65m,妈妈在照片中的高度为多少?(6分)
1.65m=165cm
解:设妈妈在照片中的高度为xcm。
3∶150= x∶165
x=3.3
答:妈妈在照片中的高度为3.3cm。
3.请你选择一个问题,把序号填在横线上,并用比例知识解答。(6分)
服装厂赶制一批衣服,原计划每天生产240件,22天能完成任务,照这样计算, ?
①机器升级,如果每天生产320件,需要几天完成?
②如果需要提前2天完成,每天需要生产多少件?
若选①
解:设需要x天完成。
320 x=240×22
x=16.5
答:需要16.5天完成。
若选②
解:设每天需要生产y件。
240×22=(22-2) y
y=264
答:每天需要生产264件。
4.为了研究二维码中的数学问题,亮亮和聪聪做了一个数学实验,操作步骤如下:
①亮亮测量了一个二维码的四条边,发现这是一个边长为2.5厘米的正方形;
②为了方便做实验,聪聪将这个二维码按20∶1放大后打印出来;
③亮亮准备了一些围棋棋子,随机扔进放大后的二维码内,他一共实验了875次,棋子落入黑色区域525次。(落人黑色区域的次数占实验总次数的几分之几就大约表示黑色区域的面积占二维码面积的几分之几)
根据上面的信息计算一下,放大后的二维码中黑色区域的面积大约是多少平方厘米?(8分)
2.5×2.5×20×20=2500(平方厘米)
2500×=1500(平方厘米)
答:放大后的二维码中黑色区域的面积大约是1500平方厘米。
