期中测试 (含答案)2024-2025学年人教版七年级数学下册
文档属性
| 名称 | 期中测试 (含答案)2024-2025学年人教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 324.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 20:06:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期中测试
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
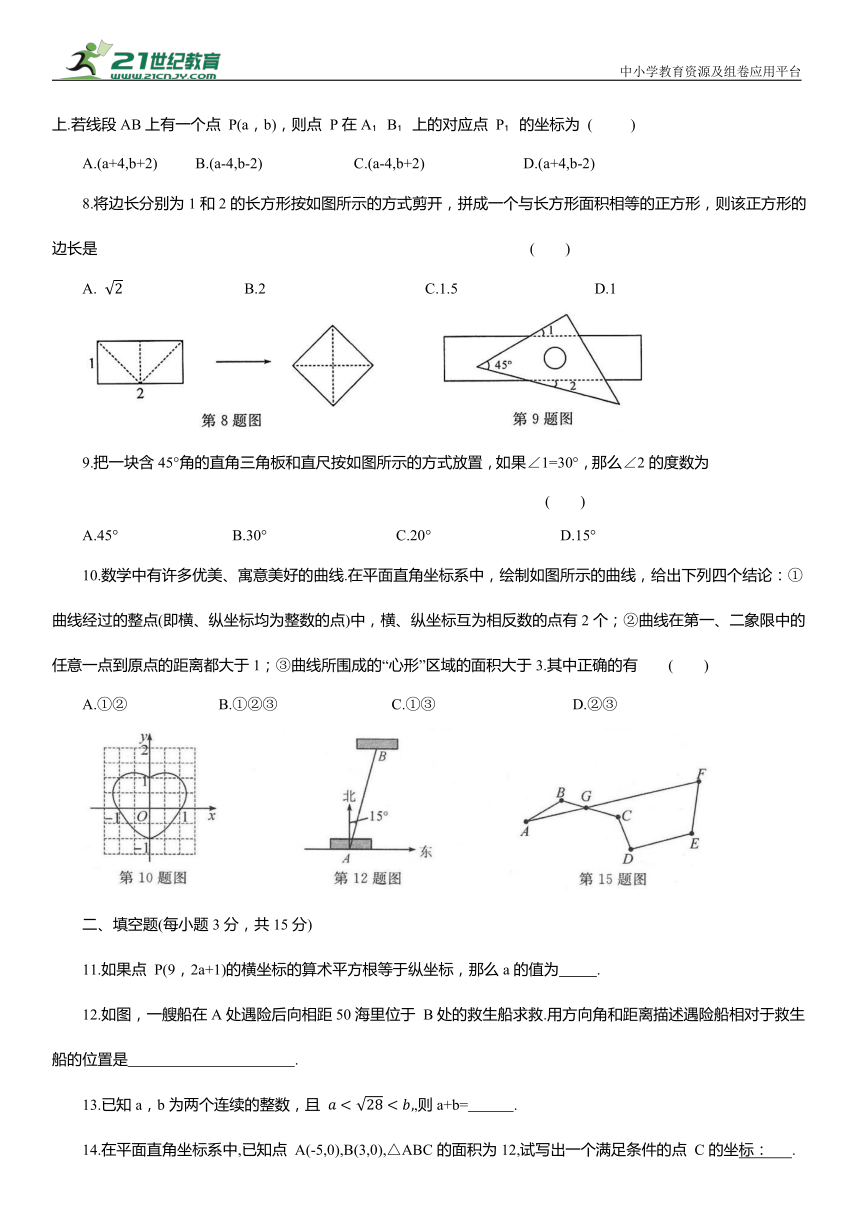
1.2024年3月31日,中国载人航天公布载人航天工程版月历,计划于4月下旬发射神舟十八号载人飞船、迎接神舟十七号乘组返回.如图,载人航天工程标识主造型像一个汉语书法的“中”字,充满中国元素和航天特色,结构优美、寓意深刻.在选项的四个图中,能由左图经过平移得到的是 ( )
2.如图,已知直线a,b被直线c 所截,则∠1 和∠2 是一对 ( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
3.在实数 中,无理数有 ( )
A.1个 B.2个 C.3个 D.4个
4.如图,直线a,b被直线c所截,下列条件能判定a∥b的是 ( )
A.∠1=∠2 B.∠3+∠4=180° C.∠1=∠4 D.∠2=30°,∠4=35°
5.下列说法不正确的是 ( )
A.±0.3是0.09的平方根,即 B.存在立方根和平方根相等的数
C.正数的两个平方根的积为负数 的平方根是±8
6.已知点 P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,线段AB经过平移得到线段A B ,其中点A,B的对应点分别为点A ,B ,这四个点都在格点上.若线段AB上有一个点 P(a,b),则点 P在A B 上的对应点 P 的坐标为 ( )
A.(a+4,b+2) B.(a-4,b-2) C.(a-4,b+2) D.(a+4,b-2)
8.将边长分别为1和2的长方形按如图所示的方式剪开,拼成一个与长方形面积相等的正方形,则该正方形的边长是 ( )
A. B.2 C.1.5 D.1
9.把一块含45°角的直角三角板和直尺按如图所示的方式放置,如果∠1=30°,那么∠2的度数为 ( )
A.45° B.30° C.20° D.15°
10.数学中有许多优美、寓意美好的曲线.在平面直角坐标系中,绘制如图所示的曲线,给出下列四个结论:①曲线经过的整点(即横、纵坐标均为整数的点)中,横、纵坐标互为相反数的点有2个;②曲线在第一、二象限中的任意一点到原点的距离都大于1;③曲线所围成的“心形”区域的面积大于3.其中正确的有 ( )
A.①② B.①②③ C.①③ D.②③
二、填空题(每小题3分,共15分)
11.如果点 P(9,2a+1)的横坐标的算术平方根等于纵坐标,那么a的值为 .
12.如图,一艘船在A处遇险后向相距50海里位于 B处的救生船求救.用方向角和距离描述遇险船相对于救生船的位置是 .
13.已知a,b为两个连续的整数,且 ,则a+b= .
14.在平面直角坐标系中,已知点 A(-5,0),B(3,0),△ABC的面积为12,试写出一个满足条件的点 C的坐标: .
15.将北斗七星的位置画到纸上,分别标为点A,B,C,D,E,F,G,然后将点A,B,C,D,E,F,A顺次首尾连接(如图所示),设AF恰好经过点G,且点 B,G,C在同一条直线上.已知AF∥DE,∠D=105°,∠C=135°,则∠CGF的度数为 ;连接AD,若AD∥BC,则∠ADE的度数为 .
三、解答题(共75分)
16.(8分)计算:
17.(9分)如图,市政府的坐标是(2,0),酒店的坐标是(4,2).
(1)请根据上述信息,在图中画出相应的平面直角坐标系.
(2)已知小明所在位置的坐标为(5,-4).
①请在图中用字母 A 标出小明的位置.
②小明先向北走了3个单位长度,再向东走了2个单位长度,此时小明所在位置的坐标是 .
18.(9分)如图,直线AB,CD相交于点O,OC平分∠BOE,∠AOE=2∠FOD.
(1)若 求∠AOD的度数.
(2)猜想OE与OF 之间的位置关系,并说明理由.
19.(9分)如图,已知AD,BC相交于点E,F,G,H分别在BC,CD,BD上,且. ∠2,∠5=∠C.求证:AB∥EH.
20.(9分)如图,某校规划一块正方形场地ABCD,设计分别与AB,AD平行的横向通道和纵向通道,其余部分铺上草皮,这4块草坪为相同的长方形,每块草坪的长与宽之比是10:9,且草坪的总面积为90 m .
(1)求每块草坪的长.
(2)若横向通道的宽是纵向通道的宽的3倍,求纵向通道的宽.
21.(10分)如图所示,在平面直角坐标系中,三角形ABC经过平移得到三角形.
(1)分别写出点 A,A'的坐标:A ,A' .
(2)请说明三角形 是由三角形ABC经过怎样的平移得到的.
(3)若点M(m,n+1)是三角形ABC内部的一点,平移后的对应点 M'的坐标为(--1,m--2),求 m 和n的值.
22.(10分)如图,在平面直角坐标系中,已知点 A(a,0),B(b,0),其中a,b满足
(1)填空:(
(2)若在第三象限内有一点 M(-2,m),请用含 m的代数式表示三角形ABM 的面积.
(3)在(2)的条件下,当 时,线段 BM与 y轴相交于点 若 P 是 y轴上的动点,当满足三角形 PBM的面积是三角形ABM 面积的2倍时,求点 P 的坐标.
23.(11分)在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含( 角的直角三角板 ”为主题开展数学活动.
(1)如图1,三角板的 角的顶点G在CD上.若∠2=2∠1,求∠1的度数.
(2)如图2,小颖把三角板的两个锐角的顶点 E,G分别放在AB 和CD 上,请探索 与 之间的数量关系.
(3)如图3,小亮把三角板的直角顶点F放在CD上,30°角的顶点 E放在AB上.若 则 与 的数量关系是什么(用含α,β的代数式表示,不写理由)
期中测试
1. D 2. D 3. B 4. C 5. D 6. A 7. C 8. A 9. D 10. D11.1 12.南偏西15°,50海里 13.11 14.(-4,3)(答案不唯一)15.30° 150°
16.解:(1)原式: (2)原式=4-
17.解:(1)图略.(2)①图略.②(7,-1)
18.解:(1)∵∠FOD=21°,∠AOE=2∠FOD,∴∠AOE=42°.∴∠BOE=180°-∠AOE=180°-42°=138°.∵OC平分∠BOE,∴ -∠COE=180°-42°-69°=69°.(2)OE⊥OF.理由如下:设 则∠AOE=2x°,∠BOE=2y°.∵∠AOE+∠BOE=180°,∴2x+2y=180.∴x+y=90,即∠DOF+∠COE=90°.∵∠EOF+∠DOF+∠COE=180°,∴∠EOF=90°.∴OE⊥OF.
19.证明:∵∠1=∠2,∴FG∥DE.∴∠3=∠GDE.∵∠3=∠4,∴∠4=∠GDE.∴EH∥CD.∴∠BEH=∠C.∵∠5=∠C,∴∠BEH=∠5.∴AB∥EH.
20.解:(1)设每块草坪的长为10xm,则宽为9xm.根据题意,得10x 解得x=±0.5.∵x>0,∴x=0.5.∴10x=5.答:每块草坪的长为5m.(2)设纵向通道的宽为 ym,则横向通道的宽为3ym.根据题意,得3y+9×0.5×2=y+5×2,解得y=0.5.答:纵向通道的宽为0.5m.
21.解:(1)(1,0) (-4,4) (2)由坐标可知,三角形A'B'C'是由三角形ABC 先向左平移5个单位长度,再向上平移4个单位长度得到的.(3)由题意,得m-5=-1,n+1+4=m-2,解得m=4,n=-3.
22.解:(1)-1 3 (2)∵a=-1,b=3,∴A(-1,0),B(3,0).∴AB=4.∵M(-2,m),且点 M在第三象限, ×4×(-m)=-2m.(3)当 时,则 又 解得 当点 P在点C 的下方时,P( 即 当点 P在点C的上方时, 即P(0, 综上所述,点P的).坐标为 或((0, ).
23.解:(1)∵AB∥CD,∴∠1=∠EGD.∵∠2+∠FGE+∠EGD=180°,∠2=2∠1,∴2∠1+60°+∠1=180°,解得∠1=40°.(2)过点 F 作 FP∥AB.∵CD∥AB,∴FP∥AB∥CD.∴∠AEF=∠EFP,∠FGC=∠GFP.∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG.∵∠EFG=90°,∴∠AEF+∠FGC=90°.(3)α+β=300°.
期中测试
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.2024年3月31日,中国载人航天公布载人航天工程版月历,计划于4月下旬发射神舟十八号载人飞船、迎接神舟十七号乘组返回.如图,载人航天工程标识主造型像一个汉语书法的“中”字,充满中国元素和航天特色,结构优美、寓意深刻.在选项的四个图中,能由左图经过平移得到的是 ( )
2.如图,已知直线a,b被直线c 所截,则∠1 和∠2 是一对 ( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
3.在实数 中,无理数有 ( )
A.1个 B.2个 C.3个 D.4个
4.如图,直线a,b被直线c所截,下列条件能判定a∥b的是 ( )
A.∠1=∠2 B.∠3+∠4=180° C.∠1=∠4 D.∠2=30°,∠4=35°
5.下列说法不正确的是 ( )
A.±0.3是0.09的平方根,即 B.存在立方根和平方根相等的数
C.正数的两个平方根的积为负数 的平方根是±8
6.已知点 P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,线段AB经过平移得到线段A B ,其中点A,B的对应点分别为点A ,B ,这四个点都在格点上.若线段AB上有一个点 P(a,b),则点 P在A B 上的对应点 P 的坐标为 ( )
A.(a+4,b+2) B.(a-4,b-2) C.(a-4,b+2) D.(a+4,b-2)
8.将边长分别为1和2的长方形按如图所示的方式剪开,拼成一个与长方形面积相等的正方形,则该正方形的边长是 ( )
A. B.2 C.1.5 D.1
9.把一块含45°角的直角三角板和直尺按如图所示的方式放置,如果∠1=30°,那么∠2的度数为 ( )
A.45° B.30° C.20° D.15°
10.数学中有许多优美、寓意美好的曲线.在平面直角坐标系中,绘制如图所示的曲线,给出下列四个结论:①曲线经过的整点(即横、纵坐标均为整数的点)中,横、纵坐标互为相反数的点有2个;②曲线在第一、二象限中的任意一点到原点的距离都大于1;③曲线所围成的“心形”区域的面积大于3.其中正确的有 ( )
A.①② B.①②③ C.①③ D.②③
二、填空题(每小题3分,共15分)
11.如果点 P(9,2a+1)的横坐标的算术平方根等于纵坐标,那么a的值为 .
12.如图,一艘船在A处遇险后向相距50海里位于 B处的救生船求救.用方向角和距离描述遇险船相对于救生船的位置是 .
13.已知a,b为两个连续的整数,且 ,则a+b= .
14.在平面直角坐标系中,已知点 A(-5,0),B(3,0),△ABC的面积为12,试写出一个满足条件的点 C的坐标: .
15.将北斗七星的位置画到纸上,分别标为点A,B,C,D,E,F,G,然后将点A,B,C,D,E,F,A顺次首尾连接(如图所示),设AF恰好经过点G,且点 B,G,C在同一条直线上.已知AF∥DE,∠D=105°,∠C=135°,则∠CGF的度数为 ;连接AD,若AD∥BC,则∠ADE的度数为 .
三、解答题(共75分)
16.(8分)计算:
17.(9分)如图,市政府的坐标是(2,0),酒店的坐标是(4,2).
(1)请根据上述信息,在图中画出相应的平面直角坐标系.
(2)已知小明所在位置的坐标为(5,-4).
①请在图中用字母 A 标出小明的位置.
②小明先向北走了3个单位长度,再向东走了2个单位长度,此时小明所在位置的坐标是 .
18.(9分)如图,直线AB,CD相交于点O,OC平分∠BOE,∠AOE=2∠FOD.
(1)若 求∠AOD的度数.
(2)猜想OE与OF 之间的位置关系,并说明理由.
19.(9分)如图,已知AD,BC相交于点E,F,G,H分别在BC,CD,BD上,且. ∠2,∠5=∠C.求证:AB∥EH.
20.(9分)如图,某校规划一块正方形场地ABCD,设计分别与AB,AD平行的横向通道和纵向通道,其余部分铺上草皮,这4块草坪为相同的长方形,每块草坪的长与宽之比是10:9,且草坪的总面积为90 m .
(1)求每块草坪的长.
(2)若横向通道的宽是纵向通道的宽的3倍,求纵向通道的宽.
21.(10分)如图所示,在平面直角坐标系中,三角形ABC经过平移得到三角形.
(1)分别写出点 A,A'的坐标:A ,A' .
(2)请说明三角形 是由三角形ABC经过怎样的平移得到的.
(3)若点M(m,n+1)是三角形ABC内部的一点,平移后的对应点 M'的坐标为(--1,m--2),求 m 和n的值.
22.(10分)如图,在平面直角坐标系中,已知点 A(a,0),B(b,0),其中a,b满足
(1)填空:(
(2)若在第三象限内有一点 M(-2,m),请用含 m的代数式表示三角形ABM 的面积.
(3)在(2)的条件下,当 时,线段 BM与 y轴相交于点 若 P 是 y轴上的动点,当满足三角形 PBM的面积是三角形ABM 面积的2倍时,求点 P 的坐标.
23.(11分)在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含( 角的直角三角板 ”为主题开展数学活动.
(1)如图1,三角板的 角的顶点G在CD上.若∠2=2∠1,求∠1的度数.
(2)如图2,小颖把三角板的两个锐角的顶点 E,G分别放在AB 和CD 上,请探索 与 之间的数量关系.
(3)如图3,小亮把三角板的直角顶点F放在CD上,30°角的顶点 E放在AB上.若 则 与 的数量关系是什么(用含α,β的代数式表示,不写理由)
期中测试
1. D 2. D 3. B 4. C 5. D 6. A 7. C 8. A 9. D 10. D11.1 12.南偏西15°,50海里 13.11 14.(-4,3)(答案不唯一)15.30° 150°
16.解:(1)原式: (2)原式=4-
17.解:(1)图略.(2)①图略.②(7,-1)
18.解:(1)∵∠FOD=21°,∠AOE=2∠FOD,∴∠AOE=42°.∴∠BOE=180°-∠AOE=180°-42°=138°.∵OC平分∠BOE,∴ -∠COE=180°-42°-69°=69°.(2)OE⊥OF.理由如下:设 则∠AOE=2x°,∠BOE=2y°.∵∠AOE+∠BOE=180°,∴2x+2y=180.∴x+y=90,即∠DOF+∠COE=90°.∵∠EOF+∠DOF+∠COE=180°,∴∠EOF=90°.∴OE⊥OF.
19.证明:∵∠1=∠2,∴FG∥DE.∴∠3=∠GDE.∵∠3=∠4,∴∠4=∠GDE.∴EH∥CD.∴∠BEH=∠C.∵∠5=∠C,∴∠BEH=∠5.∴AB∥EH.
20.解:(1)设每块草坪的长为10xm,则宽为9xm.根据题意,得10x 解得x=±0.5.∵x>0,∴x=0.5.∴10x=5.答:每块草坪的长为5m.(2)设纵向通道的宽为 ym,则横向通道的宽为3ym.根据题意,得3y+9×0.5×2=y+5×2,解得y=0.5.答:纵向通道的宽为0.5m.
21.解:(1)(1,0) (-4,4) (2)由坐标可知,三角形A'B'C'是由三角形ABC 先向左平移5个单位长度,再向上平移4个单位长度得到的.(3)由题意,得m-5=-1,n+1+4=m-2,解得m=4,n=-3.
22.解:(1)-1 3 (2)∵a=-1,b=3,∴A(-1,0),B(3,0).∴AB=4.∵M(-2,m),且点 M在第三象限, ×4×(-m)=-2m.(3)当 时,则 又 解得 当点 P在点C 的下方时,P( 即 当点 P在点C的上方时, 即P(0, 综上所述,点P的).坐标为 或((0, ).
23.解:(1)∵AB∥CD,∴∠1=∠EGD.∵∠2+∠FGE+∠EGD=180°,∠2=2∠1,∴2∠1+60°+∠1=180°,解得∠1=40°.(2)过点 F 作 FP∥AB.∵CD∥AB,∴FP∥AB∥CD.∴∠AEF=∠EFP,∠FGC=∠GFP.∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG.∵∠EFG=90°,∴∠AEF+∠FGC=90°.(3)α+β=300°.
同课章节目录
