期末复习(一) 相交线与平行线(含答案)
文档属性
| 名称 | 期末复习(一) 相交线与平行线(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 239.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 20:09:50 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
期末复习(一) 相交线与平行线
01 知识结构图
02 重难点突破
重难点1 与相交线有关的角度计算
【例1】 如图所示,直线 AB,CD相交于点O,OD 平分∠BOE,OF 平分∠AOE.
(1)判断 OF 与 OD 的位置关系,并说明理由.
(2)若∠AOC :∠AOD=1:5,求∠EOF的度数.
【思路点拨】 (1)根据OD平分∠BOE,OF平分∠AOE,求得∠FOD 的度数,从而判断OF与OD 的位置关系.
(2)根据∠AOC,∠AOD 的度数比以及邻补角的性质,求得∠AOC 的度数.然后利用“对顶角相等”得∠BOD 的度数,从而得∠EOD 的度数.最后利用(1)中∠FOD 的度数,求得∠EOF 的度数.
【解答】
方 法 指导
求角的度数问题时,要善于从图形中挖掘隐含条件,如:邻补角、对顶角,然后结合条件给出的角的和、差、倍、分等关系进行计算.
变式训练
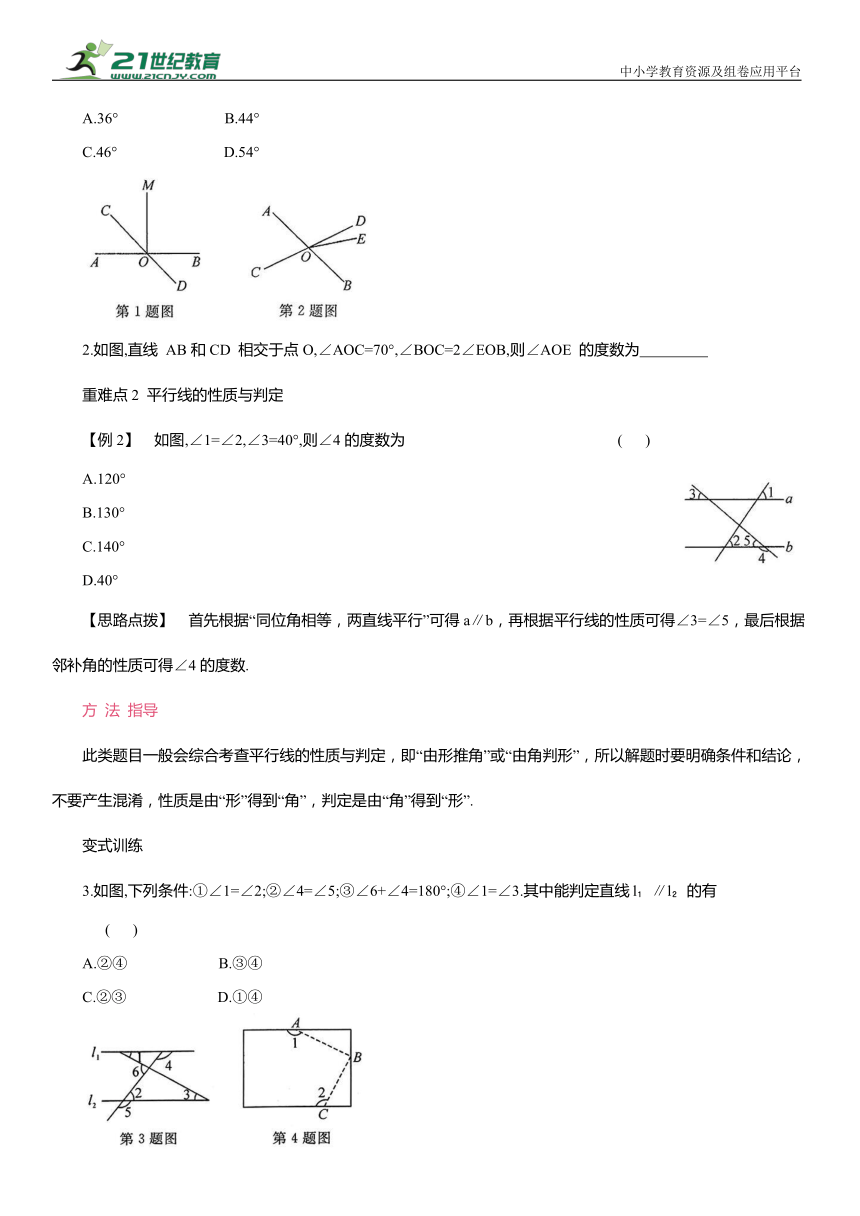
1.如图,直线AB,CD相交于点O,MO⊥AB,垂足为O.已知∠AOD=136°,则∠COM的度数为 ( )
A.36° B.44°
C.46° D.54°
2.如图,直线 AB和CD 相交于点O,∠AOC=70°,∠BOC=2∠EOB,则∠AOE 的度数为
重难点2 平行线的性质与判定
【例2】 如图,∠1=∠2,∠3=40°,则∠4的度数为 ( )
A.120°
B.130°
C.140°
D.40°
【思路点拨】 首先根据“同位角相等,两直线平行”可得a∥b,再根据平行线的性质可得∠3=∠5,最后根据邻补角的性质可得∠4的度数.
方 法 指导
此类题目一般会综合考查平行线的性质与判定,即“由形推角”或“由角判形”,所以解题时要明确条件和结论,不要产生混淆,性质是由“形”得到“角”,判定是由“角”得到“形”.
变式训练
3.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠6+∠4=180°;④∠1=∠3.其中能判定直线l ∥l 的有 ( )
A.②④ B.③④
C.②③ D.①④
4.如图,按虚线剪去长方形纸片相邻的两个角.若∠1=150°,AB⊥BC,则∠2的度数为 ( )
A.100° B.110°
C.120° D.130°
5.如图,已知直线AB∥DF,∠D+∠B=180°.
(1)求证:DE∥BC.
(2)如果∠AMD=75°,求∠AGC 的度数.
重难点3 命题
【例3】 下列四个命题:①对顶角相等;②同旁内角互补;③平移前后的两个图形面积、周长都相等;④两直线平行,同位角相等.其中是假命题的有 (填序号).
方法 指导
要说明一个命题的正确性,可根据已有知识进行推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
变式训练
6.将命题“同角的余角相等”改写成“如果 那么……”的形式:
7.新考向 开放性问题可以用来证明命题“任意偶数都是 8 的倍数”是假命题的数是 .(填一个)
重难点4 平移
【例4】 如图,将四边形 ABCD 向右平移一段距离后得到四边形A'B'C'D'.
(1)写出图中两组平行且相等的线段.
(2)写出图中四组相等的角.
(3)四边形 ABCD与四边形A'B'C'D'的形状、大小相同吗
【解答】
方 法 指导
本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
变式训练
8.如图,可以由左边的图案通过平移得到的图案是 ( )
9.某会场台阶的截面图如图所示,要在上面铺上红地毯,则至少需要 米的地毯才能铺满整个台阶 ( )
A.2.5
B.5
C.7.5
D.10
重难点突破
【例1】 解:(1)OF⊥OD.理由:∵OF 平分∠AOE,OD平分∠BOE,∴∠AOF=∠EOF= ∠AOE,∠DOE=∠BOD= ∠BOE.∴ 即∠FOD=90°.∴OF⊥OD.(2)设∠AOC=x°.∵∠AOC:∠AOD=1:5,∴∠AOD=5x°.∵∠AOC+∠AOD=180°,∴x+5x=180,解得x=30.∴∠DOE=∠BOD=∠AOC=30°.又∵∠FOD=90°,∴∠EOF=
【例2】 C
【例3】 ②
【例4】 解:(1)AB与A'B',BC与B'C'(答案不唯一).(2)∠BAD=∠B'A'D',∠ABC=∠A'B'C',∠BCD=∠B'C'D',∠ADC=∠A'D'C'(答案不唯一).(3)四边形 ABCD 与四边形A'B'C'D'的形状、大小相同.
变式训练
1. C 2.125° 3. A 4. C
5.解:(1)证明:∵AB∥DF,∴∠D+∠DHB=180°.∵∠D+∠B=180°,∴∠B=∠DHB.∴DE∥BC.(2)∵DE∥BC,∠AMD=75°,∴∠AGB=∠AMD=75°.∴∠AGC=180°-∠AGB=180°-75°=105°.
6.如果两个角是同一个角的余角,那么这两个角相等
7.4(答案不唯一) 8. D 9. C
期末复习(一) 相交线与平行线
01 知识结构图
02 重难点突破
重难点1 与相交线有关的角度计算
【例1】 如图所示,直线 AB,CD相交于点O,OD 平分∠BOE,OF 平分∠AOE.
(1)判断 OF 与 OD 的位置关系,并说明理由.
(2)若∠AOC :∠AOD=1:5,求∠EOF的度数.
【思路点拨】 (1)根据OD平分∠BOE,OF平分∠AOE,求得∠FOD 的度数,从而判断OF与OD 的位置关系.
(2)根据∠AOC,∠AOD 的度数比以及邻补角的性质,求得∠AOC 的度数.然后利用“对顶角相等”得∠BOD 的度数,从而得∠EOD 的度数.最后利用(1)中∠FOD 的度数,求得∠EOF 的度数.
【解答】
方 法 指导
求角的度数问题时,要善于从图形中挖掘隐含条件,如:邻补角、对顶角,然后结合条件给出的角的和、差、倍、分等关系进行计算.
变式训练
1.如图,直线AB,CD相交于点O,MO⊥AB,垂足为O.已知∠AOD=136°,则∠COM的度数为 ( )
A.36° B.44°
C.46° D.54°
2.如图,直线 AB和CD 相交于点O,∠AOC=70°,∠BOC=2∠EOB,则∠AOE 的度数为
重难点2 平行线的性质与判定
【例2】 如图,∠1=∠2,∠3=40°,则∠4的度数为 ( )
A.120°
B.130°
C.140°
D.40°
【思路点拨】 首先根据“同位角相等,两直线平行”可得a∥b,再根据平行线的性质可得∠3=∠5,最后根据邻补角的性质可得∠4的度数.
方 法 指导
此类题目一般会综合考查平行线的性质与判定,即“由形推角”或“由角判形”,所以解题时要明确条件和结论,不要产生混淆,性质是由“形”得到“角”,判定是由“角”得到“形”.
变式训练
3.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠6+∠4=180°;④∠1=∠3.其中能判定直线l ∥l 的有 ( )
A.②④ B.③④
C.②③ D.①④
4.如图,按虚线剪去长方形纸片相邻的两个角.若∠1=150°,AB⊥BC,则∠2的度数为 ( )
A.100° B.110°
C.120° D.130°
5.如图,已知直线AB∥DF,∠D+∠B=180°.
(1)求证:DE∥BC.
(2)如果∠AMD=75°,求∠AGC 的度数.
重难点3 命题
【例3】 下列四个命题:①对顶角相等;②同旁内角互补;③平移前后的两个图形面积、周长都相等;④两直线平行,同位角相等.其中是假命题的有 (填序号).
方法 指导
要说明一个命题的正确性,可根据已有知识进行推理、论证,而判断一个命题是假命题,只需举出一个反例即可.
变式训练
6.将命题“同角的余角相等”改写成“如果 那么……”的形式:
7.新考向 开放性问题可以用来证明命题“任意偶数都是 8 的倍数”是假命题的数是 .(填一个)
重难点4 平移
【例4】 如图,将四边形 ABCD 向右平移一段距离后得到四边形A'B'C'D'.
(1)写出图中两组平行且相等的线段.
(2)写出图中四组相等的角.
(3)四边形 ABCD与四边形A'B'C'D'的形状、大小相同吗
【解答】
方 法 指导
本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
变式训练
8.如图,可以由左边的图案通过平移得到的图案是 ( )
9.某会场台阶的截面图如图所示,要在上面铺上红地毯,则至少需要 米的地毯才能铺满整个台阶 ( )
A.2.5
B.5
C.7.5
D.10
重难点突破
【例1】 解:(1)OF⊥OD.理由:∵OF 平分∠AOE,OD平分∠BOE,∴∠AOF=∠EOF= ∠AOE,∠DOE=∠BOD= ∠BOE.∴ 即∠FOD=90°.∴OF⊥OD.(2)设∠AOC=x°.∵∠AOC:∠AOD=1:5,∴∠AOD=5x°.∵∠AOC+∠AOD=180°,∴x+5x=180,解得x=30.∴∠DOE=∠BOD=∠AOC=30°.又∵∠FOD=90°,∴∠EOF=
【例2】 C
【例3】 ②
【例4】 解:(1)AB与A'B',BC与B'C'(答案不唯一).(2)∠BAD=∠B'A'D',∠ABC=∠A'B'C',∠BCD=∠B'C'D',∠ADC=∠A'D'C'(答案不唯一).(3)四边形 ABCD 与四边形A'B'C'D'的形状、大小相同.
变式训练
1. C 2.125° 3. A 4. C
5.解:(1)证明:∵AB∥DF,∴∠D+∠DHB=180°.∵∠D+∠B=180°,∴∠B=∠DHB.∴DE∥BC.(2)∵DE∥BC,∠AMD=75°,∴∠AGB=∠AMD=75°.∴∠AGC=180°-∠AGB=180°-75°=105°.
6.如果两个角是同一个角的余角,那么这两个角相等
7.4(答案不唯一) 8. D 9. C
同课章节目录
