广东省汕头市潮阳区2024—2025学年九年级下学期数学模拟考试试卷(含解析)
文档属性
| 名称 | 广东省汕头市潮阳区2024—2025学年九年级下学期数学模拟考试试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 20:18:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024—2025学年度广东省九年级数学模拟考试
一、选择题(每小题3分,共30分)
1.在这四个数中,最小的数是( )
A. B. C.0 D.
2.计算的结果是( )
A. B. C. D.
3.下列各点中,在第三象限的点是( )
A. B. C. D.
4.“数形结合”是研究函数的重要思想方法,如果拋物线只经过两个象限,那么的取值范围是( )
A. B. C. D.
5.一个几何体的俯视图如图所示,则这个几何体可能是( )
A. B. C. D.
6.一个正多边形的每个外角度数都等于,则这个多边形的边数为( )
A.4 B.5 C.6 D.8
7.化学方程式是用化学式来表示物质化学反应的式子.化学方程式不仅表明了反应物、生成物和反应条件,同时化学计量数代表了各反应物、生成物物质的量关系.例如就表示两份(氢气)与一份(氧气)点燃生成两份的(水).依据化学反应过程中的质量守恒定律,在化学方程式等号左边和等号右边同一元素原子的个数一定相同.已知,由此可列出关于x,y的二元一次方程为( )
A. B.
C. D.
8.如图,等边内接于,已知的半径为2,则图中的阴影部分面积为( )
A. B. C. D.
9.在反比例函数的图象上有两点,,当时,有,则的取值范围是( )
A. B. C. D.
10.俗语有云:“一天不练手脚慢,两天不练丢一半,三天不练门外汉,四天不练瞪眼看.”其意思是知识和技艺在学习后,如果不及时复习,那么学习过的东西就会被遗忘.假设每天“遗忘”的百分比是一样的,根据“两天不练丢一半”,则每天“遗忘”的百分比约为(参考数据:)( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.分解因式:a3-a=
12.若二次根式有意义,则x的取值范围为 .
13.ChatGPT是人工智能研究实验室OpenAI新推出的一种人工智能技术驱动的自然语言处理工具,ChatGPT的背后离不开大模型、大数据、大算力,其技术底座有多达1750亿个模型参数,数据1750亿用科学记数法表示为 .
14.如图,直线与直线相交于点,则关于x的方程的解为 .
15.如图正方形的边长为3,E是上一点且,F是线段上的动点.连接,将线段绕点C逆时针旋转 90°得到,连接,则的最小值是 .
三、解答题(每小题7分,共21分)
16.解不等式组:.
17.计算:.
18.为传承我国传统节日文化,端午节前夕,某校组织了包粽子活动.已知七(3)班甲组同学平均每小时比乙组多包20个粽子,甲组包150个粽子所用的时间与乙组包120个粽子所用的时间相同.求甲,乙两组同学平均每小时各包多少个粽子.
四、解答题(每小题9分,共27分)
19.如图所示,在平行四边形中,对角线与相交于点O,且,,.
(1)求证:;
(2)E,F分别是和的中点,连接,,求证:四边形是菱形.
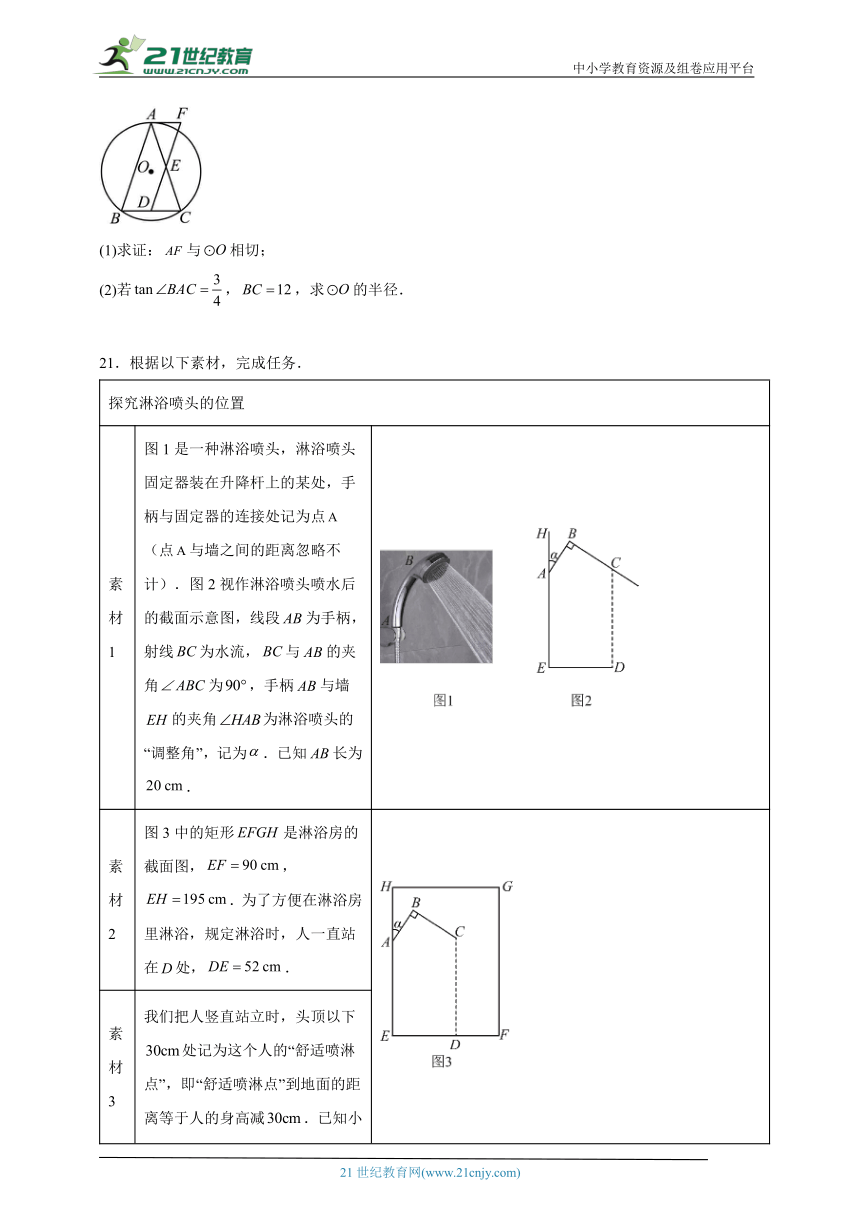
20.如图,已知是的外接圆,,点,分别是,的中点,连接并延长至点,使,连接.
(1)求证:与相切;
(2)若,,求的半径.
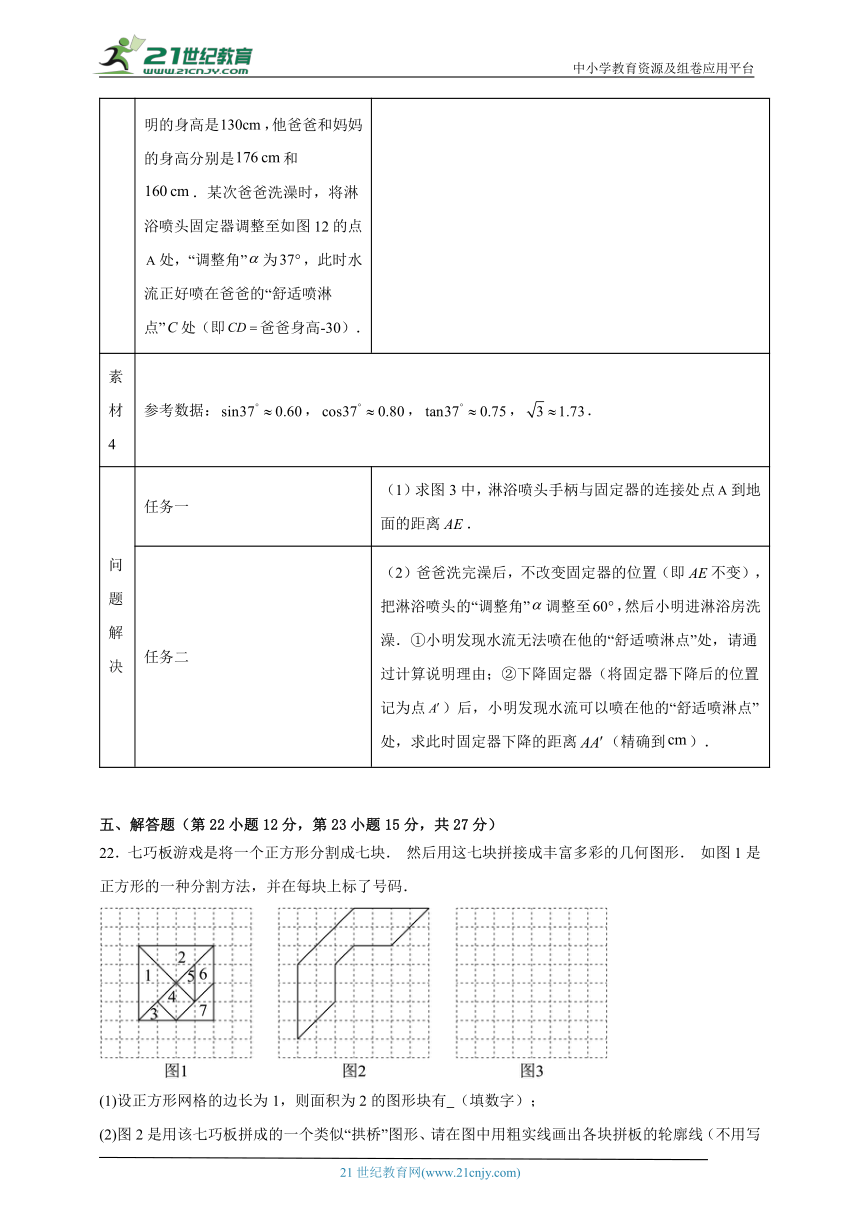
21.根据以下素材,完成任务.
探究淋浴喷头的位置
素材1 图1是一种淋浴喷头,淋浴喷头固定器装在升降杆上的某处,手柄与固定器的连接处记为点(点与墙之间的距离忽略不计).图2视作淋浴喷头喷水后的截面示意图,线段为手柄,射线为水流,与的夹角为,手柄与墙的夹角为淋浴喷头的“调整角”,记为.已知长为.
素材2 图3中的矩形是淋浴房的截面图,,.为了方便在淋浴房里淋浴,规定淋浴时,人一直站在处,.
素材3 我们把人竖直站立时,头顶以下处记为这个人的“舒适喷淋点”,即“舒适喷淋点”到地面的距离等于人的身高减.已知小明的身高是,他爸爸和妈妈的身高分别是和.某次爸爸洗澡时,将淋浴喷头固定器调整至如图12的点处,“调整角”为,此时水流正好喷在爸爸的“舒适喷淋点”处(即爸爸身高-30).
素材4 参考数据:,,,.
问题解决 任务一 (1)求图3中,淋浴喷头手柄与固定器的连接处点到地面的距离.
任务二 (2)爸爸洗完澡后,不改变固定器的位置(即不变),把淋浴喷头的“调整角”调整至,然后小明进淋浴房洗澡.①小明发现水流无法喷在他的“舒适喷淋点”处,请通过计算说明理由;②下降固定器(将固定器下降后的位置记为点)后,小明发现水流可以喷在他的“舒适喷淋点”处,求此时固定器下降的距离(精确到).
五、解答题(第22小题12分,第23小题15分,共27分)
22.七巧板游戏是将一个正方形分割成七块. 然后用这七块拼接成丰富多彩的几何图形. 如图1是正方形的一种分割方法,并在每块上标了号码.
(1)设正方形网格的边长为1,则面积为2的图形块有 (填数字);
(2)图2是用该七巧板拼成的一个类似“拱桥”图形、请在图中用粗实线画出各块拼板的轮廓线(不用写号码);
(3)请从图1的七巧板之中选五块板拼接成一个正方形,在图3中画出拼接后的示意图(标上号码),要求无重叠无缝隙,并写出该正方形的面积.
23.【问题提出】
(1)如图①,已知直线,点A,B在直线a上,点C,D在直线b上,则 ;(填“>”“<”或“=”)
【问题探究】
(2)如图②,的直径为20,点A,B,C都在上,,求面积的最大值;
【问题解决】
(3)如图③,为某市一块空地示意图,米,米,根据设计要求,现要在外选择一点D,将这块地扩大改造为一个四边形便民服务区,要求点D为内部一点,且,为服务区内两条主步道,在上修建一个引导台点E,使,再修建两条新的小道,为了让服务区功能更加合理,要使四边形的面积尽可能大,请求出满足设计要求的四边形面积的最大值.
答案和解析
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C A C C D A D C
1.D
【分析】本题主要考查了实数的大小比较,掌握负数小于零、负数的绝对值越大、自身反而越小成为解题的关键.
直接比较各数的大小即可解答.
【详解】解:∵,
∴最小的是,D选项符合题意.
故选D.
2.C
【分析】本题考查积的乘方与幂的乘方,熟练掌握积的乘方与幂的乘方的运算法则是解题的关键,根据积的乘方与幂的乘方的运算法则计算即可得到答案.
【详解】解:,
故选:C.
3.C
【分析】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.根据平面直角坐标系中各个象限的点的坐标的符号特点即可解答.
【详解】解:∵第三象限的点的坐标特点是横纵坐标均小于0,
∴结合四个选项中只有符合条件.
故选:C.
4.A
【分析】本题考查二次函数图象与系数的关系,二次函数的图象与性质,解答本题的关键是利用数形结合的思想解答.
根据抛物线只经过两个象限,且抛物线开口向上,得出最小值大于等于,即可解答.
【详解】解:,
抛物线开口向上,对称轴,顶点坐标为,
拋物线只经过两个象限,
,
,
故选:A.
5.C
【分析】本题考查了由三视图判断几何体的知识,考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.根据俯视图是从上面看到的图形解答即可.
【详解】解:A.圆柱的俯视图是圆,不符合题意;
B.横放的棱柱的俯视图是矩形,不符合题意;
C.圆锥的俯视图是带圆心的圆,符合题意;
D.圆台的俯视图是圆环,不符合题意;
故选:C.
6.C
【分析】本题考查多边形的外角和,解题的关键是掌握多边形的外角和等于,根据正多边形的每个内角相等,每个外角也相等,外角和等于,即可得出答案.
【详解】解:∵多边形的外角和等于,且这个每个外角都等于,
∴它的边数为.
故选:C.
7.D
【分析】本题考查了列二元一次方程,正确找出等量关系是解题的关键,根据题意列出方程求解即可.
【详解】解:∵化学方程式等号左边和等号右边氧元素原子的个数一定相同,
∴.
故选∶D.
8.A
【分析】本题考查的是三角形的外接圆与外心、扇形面积的计算.先求得,,据此求解即可.
【详解】解:连接,连接并延长交于H,则.
∵是等边三角形,
∴,,
∴,则,
由圆周角定理得,,
∴图中的阴影部分面积.
故选A.
9.D
【分析】本题主要考查反比例函数的性质.首先根据题意,判断函数图象所在象限,再根据所在象限得到,进而求解,即可解题.
【详解】解:∵当时,有,
∴反比例函数图象在一、三象限,
∴,
∴,
故选:D.
10.C
【分析】该题主要考查了一元二次方程的应用,解题的关键是读懂题意,正确列出方程.
设每天遗忘的百分比为,根据“两天不练丢一半”列出方程解答即可.
【详解】解:设每天遗忘的百分比为,
则,
解得:.
故选:C.
11.
【详解】解:a3-a
=a(a2-1)
=
故答案为:
12.x≥﹣.
【详解】考点:二次根式有意义的条件.
根据二次根式的意义,被开方数是非负数求解.
解:根据题意得:1+2x≥0,
解得x≥-.
故答案为x≥-.
13.
【分析】本题主要考查了科学记数法的表示方法,科学记数法的表现形式为的形式,其中,为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,是正整数,由此进行求解即可得到答案.熟练掌握科学记数法的表示方法是解题的关键.
【详解】解:亿.
故答案为:.
14.
【分析】本题主要考查了一次函数与一元一次方程,首先利用函数解析式求出m的值,然后再根据两函数图象的交点横坐标就是关于x的方程的解可得答案.
【详解】解:∵直线与直线相交于点,
∴,
∴,
∴,
∴当时,,
∴关于x的方程的解是,
故答案为:.
15.
【分析】如图,连接BG.由△CBG≌△CDF,推出∠CBG=∠CDF,因为∠CDF是定值,推出点G在射线BG上运动,且tan∠CBG=tan∠CDF==,根据垂线段最短可知,当EG⊥BG时,EG的长最短.
【详解】解:如图,作射线BG.
∵四边形ABCD是正方形,
∴CB=CD,∠BCD=90°,
∵∠FCG=∠DCB=90°,
∴∠BCG+∠BCF=90°,∠DCF+∠BCF=90°,
∴∠BCG=∠DCF,
在△CBG和△CDF中
,
∴△CBG≌△CDF,
∴∠CBG=∠CDF,
∵∠CDF是定值,
∴点G在射线BG上运动,且tan∠CBG=tan∠CDF==,
根据垂线段最短可知,当EG⊥BG时,EG的长最短,
此时tan∠EBG==,设EG=m,则BG=3m,
在Rt△BEG中,
∵BE2=BG2+EG2,
∴4=m2+9m2,
∴m=(负根已经舍弃),
∴EG的最小值为,
故答案为.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质,垂线段最短等知识,熟练掌握全等三角形的判定与性质,相似三角形的判定与性质,垂线段最短是解答本题的关键.
16.原不等式组的解集是.
【分析】本题考查了解一元一次不等式组.先求出不等式组中每个不等式的解集,再根据确定不等式组解集的方法“同大取大;同小取小;大小小大中间找;大大小小找不到”得出答案.
【详解】解:解,得,
解,得,
原不等式组的解集是.
17.
【分析】本题考查了实数的混合运算,利用负整数指数幂、绝对值、零指数幂、特殊角的三角函数值、立方根的定义分别化简,再合并即可求解,掌握实数的运算法则是解题的关键.
【详解】解:
,
,
.
18.甲组平均每小时包100个粽子,乙组平均每小时包80个粽子.
【分析】本题主要考查了分式方程的实际应用.设乙组每小时包个粽子,则甲组每小时包个粽子,根据时间等于总工作量除以工作效率,即可得出关于的分式方程,解之并检验后即可得出结果.
【详解】解:设乙组平均每小时包个粽子,则甲组平均每小时包个粽子,
由题意得:
,解得:,
经检验:是分式方程的解,且符合题意,
∴分式方程的解为:,
∴
答:甲组平均每小时包100个粽子,乙组平均每小时包80个粽子.
19.(1)见解析
(2)见解析
【分析】(1)利用平行四边形性质得到,,再利用勾股定理逆定理得到为直角三角形,即可证明;
(2)利用直角三角形性质和线段中点的特点,得到,,结合平行四边形性质得到,进而证明四边形是平行四边形,再根据,即可证明平行四边形是菱形.
本题考查平行四边形性质和判定,勾股定理逆定理,直角三角形性质,线段中点的特点,菱形的判定,熟练掌握运用这些判定和性质是解题关键.
【详解】(1)证明:在平行四边形中,对角线与相交于点O,,,
,.
,
,即,
为直角三角形,,
.
(2)证明:由(1)知为直角三角形.
E,F分别是和的中点,
,.
四边形是平行四边形,
,,
,
四边形是平行四边形.
又∵,
平行四边形是菱形.
20.(1)见解析
(2)的半径为10
【分析】(1)先证明四边形是平行四边形,得到,连接,,,三线合一结合平行线的性质,推出,即可得证;
(2)圆周角定理推出,解直角三角形求出圆的半径即可.
【详解】(1)证明:,分别是,的中点,
是的中位线,
,.
,
,
,
四边形是平行四边形,
.
如图,连接,,,
,
,即是的垂直平分线.
,
点在的垂直平分线上,即点,,共线.
,
,
又是的半径,
与相切.
(2)解:,,
,.
,
.
在中,,
,解之,得.
,
的半径为10.
【点睛】本题考查三角形的中位线定理,平行四边形的判定和性质,圆周角定理,切线的判定,解直角三角形,熟练掌握相关知识点,是解题的关键.
21.(1);(2)①理由见解析;②
【分析】本题考查解直角三角形的应用.把所给的角度整理到直角三角形中并进行解答是解决本题的关键.
(1)作于点N,延长交于点M,利用的正弦值和余弦值可得和的长度,进而可得的长度,那么根据的正切值可得的长度,那么的长度即为的长度减去的长度;
(2)①利用的正弦值和余弦值可得和的长度,进而可得的长度,那么根据的正切值可得的长度,那么的长度即为NE的长度减去的长度;
②设点A移动到了点,易得进而求得的长度,取的长度,减去的长度,即为固定器下降的距离.
【详解】解:(1)作于点N,延长交于点M,则,
∵爸爸身高是,此时水流正好喷在爸爸的“舒适喷淋点”C处,
∴,
∵
∴,
∵,
∴,
∴,
∴,
∴,
∴.
答:点A到地面的距离约为;
(2)①当时,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵小明的身高是,
∴小明的舒适距离,
∵,
∴水流无法喷在小明的“舒适喷淋点”处;
②设点A移动到了点,此时在小明的“舒适喷淋点”,
∴,
由题意得:,
∴,
∴.
答:固定器下降的距离约为.
22.(1)4,6,7
(2)见解析
(3)见解析,正方形的面积为8.
【分析】本题考查了正方形的性质,概率公式,七巧板,三角形的面积,熟练掌握七巧板是解题的关键.
(1)先计算出各个图块的面积,可得出答案;
(2)根据题意用七巧板拼成的一个类似“拱桥”图形即可;
(3)依据题意,在图2中画出拼接后的示意图,再计算出面积即可.
【详解】(1)解:正方形网格的边长为1,则面积为2的图形块有
图形块1,2的面积为:,
图形块3的面积为:,
图形块4的面积为:,
图形块5的面积为:,
图形块6的面积为:,
图形块7的面积为:,
面积为2的图形块有4,6,7,
故答案为:4,6,7;
(2)解:如图所示,
(3)解:如图所示,
正方形的面积为8.
23.(1)=;(2)108;(3)平方米.
【分析】(1)由平行线的性质,根据同底等高的两三角形面积相等作答;
(2)长不变,只要边上的高最大,面积最大;由图知当C是优弧的中点时,边上的高最大,面积最大,求得优弧的中点到的距离就可求得最大面积;
(3)过C作交的延长线于F,得,先证得四边形的面积的面积;根据得点F在以为边向外作的等边的外接圆上,受解决(2)的启发得,当F运动到点G时,的面积最大,即四边形的面积最大.最后计算出的面积即是四边形的面积最大值.
【详解】解:(1)如图①所示,分别过A、B两点向直线b作垂线,垂足为M、N,
∵
∴,
∴四边形是矩形,
∴,
∴
又,
∴;
故答案为:=;
(2)如图②,取优弧的中点记为,过作的垂线,垂足为D,
由垂径定理知过点O,且.
过点C作的平行线,
当直线向上平移时,与的距离增大,即的边上的高增大,
∴当CE运动到最高点C时,的边上的高最大.
又为定值,
∴当C运动到时,的面积最大,
连接,
,的直径为20,
,
在中,.
.
的面积为.
面积的最大值为108.
(3)如图,过点C作交的延长线于F.
.
.
,
四边形是平行四边形.
.
,
.
.
又由(1)的结论知,
.
所以只需求得最大值即得的最大值.
以AC为边向外作等边,再作等边的外接圆,过点G作于点J.如图,
,
点F在的外接圆上.
由第(2)问的解决知,当点F运动到点G时,.
在中,(米),
(米),
(米),
(平方米).
四边形面积的最大值为平方米.
【点睛】本题考查了三角形等积变形、定角对定边的三角形的面积最大值、等边三角形及其外接圆、平行四边形的判定和性质等考点,熟练掌握相关知识并能综合应用是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024—2025学年度广东省九年级数学模拟考试
一、选择题(每小题3分,共30分)
1.在这四个数中,最小的数是( )
A. B. C.0 D.
2.计算的结果是( )
A. B. C. D.
3.下列各点中,在第三象限的点是( )
A. B. C. D.
4.“数形结合”是研究函数的重要思想方法,如果拋物线只经过两个象限,那么的取值范围是( )
A. B. C. D.
5.一个几何体的俯视图如图所示,则这个几何体可能是( )
A. B. C. D.
6.一个正多边形的每个外角度数都等于,则这个多边形的边数为( )
A.4 B.5 C.6 D.8
7.化学方程式是用化学式来表示物质化学反应的式子.化学方程式不仅表明了反应物、生成物和反应条件,同时化学计量数代表了各反应物、生成物物质的量关系.例如就表示两份(氢气)与一份(氧气)点燃生成两份的(水).依据化学反应过程中的质量守恒定律,在化学方程式等号左边和等号右边同一元素原子的个数一定相同.已知,由此可列出关于x,y的二元一次方程为( )
A. B.
C. D.
8.如图,等边内接于,已知的半径为2,则图中的阴影部分面积为( )
A. B. C. D.
9.在反比例函数的图象上有两点,,当时,有,则的取值范围是( )
A. B. C. D.
10.俗语有云:“一天不练手脚慢,两天不练丢一半,三天不练门外汉,四天不练瞪眼看.”其意思是知识和技艺在学习后,如果不及时复习,那么学习过的东西就会被遗忘.假设每天“遗忘”的百分比是一样的,根据“两天不练丢一半”,则每天“遗忘”的百分比约为(参考数据:)( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.分解因式:a3-a=
12.若二次根式有意义,则x的取值范围为 .
13.ChatGPT是人工智能研究实验室OpenAI新推出的一种人工智能技术驱动的自然语言处理工具,ChatGPT的背后离不开大模型、大数据、大算力,其技术底座有多达1750亿个模型参数,数据1750亿用科学记数法表示为 .
14.如图,直线与直线相交于点,则关于x的方程的解为 .
15.如图正方形的边长为3,E是上一点且,F是线段上的动点.连接,将线段绕点C逆时针旋转 90°得到,连接,则的最小值是 .
三、解答题(每小题7分,共21分)
16.解不等式组:.
17.计算:.
18.为传承我国传统节日文化,端午节前夕,某校组织了包粽子活动.已知七(3)班甲组同学平均每小时比乙组多包20个粽子,甲组包150个粽子所用的时间与乙组包120个粽子所用的时间相同.求甲,乙两组同学平均每小时各包多少个粽子.
四、解答题(每小题9分,共27分)
19.如图所示,在平行四边形中,对角线与相交于点O,且,,.
(1)求证:;
(2)E,F分别是和的中点,连接,,求证:四边形是菱形.
20.如图,已知是的外接圆,,点,分别是,的中点,连接并延长至点,使,连接.
(1)求证:与相切;
(2)若,,求的半径.
21.根据以下素材,完成任务.
探究淋浴喷头的位置
素材1 图1是一种淋浴喷头,淋浴喷头固定器装在升降杆上的某处,手柄与固定器的连接处记为点(点与墙之间的距离忽略不计).图2视作淋浴喷头喷水后的截面示意图,线段为手柄,射线为水流,与的夹角为,手柄与墙的夹角为淋浴喷头的“调整角”,记为.已知长为.
素材2 图3中的矩形是淋浴房的截面图,,.为了方便在淋浴房里淋浴,规定淋浴时,人一直站在处,.
素材3 我们把人竖直站立时,头顶以下处记为这个人的“舒适喷淋点”,即“舒适喷淋点”到地面的距离等于人的身高减.已知小明的身高是,他爸爸和妈妈的身高分别是和.某次爸爸洗澡时,将淋浴喷头固定器调整至如图12的点处,“调整角”为,此时水流正好喷在爸爸的“舒适喷淋点”处(即爸爸身高-30).
素材4 参考数据:,,,.
问题解决 任务一 (1)求图3中,淋浴喷头手柄与固定器的连接处点到地面的距离.
任务二 (2)爸爸洗完澡后,不改变固定器的位置(即不变),把淋浴喷头的“调整角”调整至,然后小明进淋浴房洗澡.①小明发现水流无法喷在他的“舒适喷淋点”处,请通过计算说明理由;②下降固定器(将固定器下降后的位置记为点)后,小明发现水流可以喷在他的“舒适喷淋点”处,求此时固定器下降的距离(精确到).
五、解答题(第22小题12分,第23小题15分,共27分)
22.七巧板游戏是将一个正方形分割成七块. 然后用这七块拼接成丰富多彩的几何图形. 如图1是正方形的一种分割方法,并在每块上标了号码.
(1)设正方形网格的边长为1,则面积为2的图形块有 (填数字);
(2)图2是用该七巧板拼成的一个类似“拱桥”图形、请在图中用粗实线画出各块拼板的轮廓线(不用写号码);
(3)请从图1的七巧板之中选五块板拼接成一个正方形,在图3中画出拼接后的示意图(标上号码),要求无重叠无缝隙,并写出该正方形的面积.
23.【问题提出】
(1)如图①,已知直线,点A,B在直线a上,点C,D在直线b上,则 ;(填“>”“<”或“=”)
【问题探究】
(2)如图②,的直径为20,点A,B,C都在上,,求面积的最大值;
【问题解决】
(3)如图③,为某市一块空地示意图,米,米,根据设计要求,现要在外选择一点D,将这块地扩大改造为一个四边形便民服务区,要求点D为内部一点,且,为服务区内两条主步道,在上修建一个引导台点E,使,再修建两条新的小道,为了让服务区功能更加合理,要使四边形的面积尽可能大,请求出满足设计要求的四边形面积的最大值.
答案和解析
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C A C C D A D C
1.D
【分析】本题主要考查了实数的大小比较,掌握负数小于零、负数的绝对值越大、自身反而越小成为解题的关键.
直接比较各数的大小即可解答.
【详解】解:∵,
∴最小的是,D选项符合题意.
故选D.
2.C
【分析】本题考查积的乘方与幂的乘方,熟练掌握积的乘方与幂的乘方的运算法则是解题的关键,根据积的乘方与幂的乘方的运算法则计算即可得到答案.
【详解】解:,
故选:C.
3.C
【分析】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.根据平面直角坐标系中各个象限的点的坐标的符号特点即可解答.
【详解】解:∵第三象限的点的坐标特点是横纵坐标均小于0,
∴结合四个选项中只有符合条件.
故选:C.
4.A
【分析】本题考查二次函数图象与系数的关系,二次函数的图象与性质,解答本题的关键是利用数形结合的思想解答.
根据抛物线只经过两个象限,且抛物线开口向上,得出最小值大于等于,即可解答.
【详解】解:,
抛物线开口向上,对称轴,顶点坐标为,
拋物线只经过两个象限,
,
,
故选:A.
5.C
【分析】本题考查了由三视图判断几何体的知识,考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.根据俯视图是从上面看到的图形解答即可.
【详解】解:A.圆柱的俯视图是圆,不符合题意;
B.横放的棱柱的俯视图是矩形,不符合题意;
C.圆锥的俯视图是带圆心的圆,符合题意;
D.圆台的俯视图是圆环,不符合题意;
故选:C.
6.C
【分析】本题考查多边形的外角和,解题的关键是掌握多边形的外角和等于,根据正多边形的每个内角相等,每个外角也相等,外角和等于,即可得出答案.
【详解】解:∵多边形的外角和等于,且这个每个外角都等于,
∴它的边数为.
故选:C.
7.D
【分析】本题考查了列二元一次方程,正确找出等量关系是解题的关键,根据题意列出方程求解即可.
【详解】解:∵化学方程式等号左边和等号右边氧元素原子的个数一定相同,
∴.
故选∶D.
8.A
【分析】本题考查的是三角形的外接圆与外心、扇形面积的计算.先求得,,据此求解即可.
【详解】解:连接,连接并延长交于H,则.
∵是等边三角形,
∴,,
∴,则,
由圆周角定理得,,
∴图中的阴影部分面积.
故选A.
9.D
【分析】本题主要考查反比例函数的性质.首先根据题意,判断函数图象所在象限,再根据所在象限得到,进而求解,即可解题.
【详解】解:∵当时,有,
∴反比例函数图象在一、三象限,
∴,
∴,
故选:D.
10.C
【分析】该题主要考查了一元二次方程的应用,解题的关键是读懂题意,正确列出方程.
设每天遗忘的百分比为,根据“两天不练丢一半”列出方程解答即可.
【详解】解:设每天遗忘的百分比为,
则,
解得:.
故选:C.
11.
【详解】解:a3-a
=a(a2-1)
=
故答案为:
12.x≥﹣.
【详解】考点:二次根式有意义的条件.
根据二次根式的意义,被开方数是非负数求解.
解:根据题意得:1+2x≥0,
解得x≥-.
故答案为x≥-.
13.
【分析】本题主要考查了科学记数法的表示方法,科学记数法的表现形式为的形式,其中,为整数,确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,是正整数,由此进行求解即可得到答案.熟练掌握科学记数法的表示方法是解题的关键.
【详解】解:亿.
故答案为:.
14.
【分析】本题主要考查了一次函数与一元一次方程,首先利用函数解析式求出m的值,然后再根据两函数图象的交点横坐标就是关于x的方程的解可得答案.
【详解】解:∵直线与直线相交于点,
∴,
∴,
∴,
∴当时,,
∴关于x的方程的解是,
故答案为:.
15.
【分析】如图,连接BG.由△CBG≌△CDF,推出∠CBG=∠CDF,因为∠CDF是定值,推出点G在射线BG上运动,且tan∠CBG=tan∠CDF==,根据垂线段最短可知,当EG⊥BG时,EG的长最短.
【详解】解:如图,作射线BG.
∵四边形ABCD是正方形,
∴CB=CD,∠BCD=90°,
∵∠FCG=∠DCB=90°,
∴∠BCG+∠BCF=90°,∠DCF+∠BCF=90°,
∴∠BCG=∠DCF,
在△CBG和△CDF中
,
∴△CBG≌△CDF,
∴∠CBG=∠CDF,
∵∠CDF是定值,
∴点G在射线BG上运动,且tan∠CBG=tan∠CDF==,
根据垂线段最短可知,当EG⊥BG时,EG的长最短,
此时tan∠EBG==,设EG=m,则BG=3m,
在Rt△BEG中,
∵BE2=BG2+EG2,
∴4=m2+9m2,
∴m=(负根已经舍弃),
∴EG的最小值为,
故答案为.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质,垂线段最短等知识,熟练掌握全等三角形的判定与性质,相似三角形的判定与性质,垂线段最短是解答本题的关键.
16.原不等式组的解集是.
【分析】本题考查了解一元一次不等式组.先求出不等式组中每个不等式的解集,再根据确定不等式组解集的方法“同大取大;同小取小;大小小大中间找;大大小小找不到”得出答案.
【详解】解:解,得,
解,得,
原不等式组的解集是.
17.
【分析】本题考查了实数的混合运算,利用负整数指数幂、绝对值、零指数幂、特殊角的三角函数值、立方根的定义分别化简,再合并即可求解,掌握实数的运算法则是解题的关键.
【详解】解:
,
,
.
18.甲组平均每小时包100个粽子,乙组平均每小时包80个粽子.
【分析】本题主要考查了分式方程的实际应用.设乙组每小时包个粽子,则甲组每小时包个粽子,根据时间等于总工作量除以工作效率,即可得出关于的分式方程,解之并检验后即可得出结果.
【详解】解:设乙组平均每小时包个粽子,则甲组平均每小时包个粽子,
由题意得:
,解得:,
经检验:是分式方程的解,且符合题意,
∴分式方程的解为:,
∴
答:甲组平均每小时包100个粽子,乙组平均每小时包80个粽子.
19.(1)见解析
(2)见解析
【分析】(1)利用平行四边形性质得到,,再利用勾股定理逆定理得到为直角三角形,即可证明;
(2)利用直角三角形性质和线段中点的特点,得到,,结合平行四边形性质得到,进而证明四边形是平行四边形,再根据,即可证明平行四边形是菱形.
本题考查平行四边形性质和判定,勾股定理逆定理,直角三角形性质,线段中点的特点,菱形的判定,熟练掌握运用这些判定和性质是解题关键.
【详解】(1)证明:在平行四边形中,对角线与相交于点O,,,
,.
,
,即,
为直角三角形,,
.
(2)证明:由(1)知为直角三角形.
E,F分别是和的中点,
,.
四边形是平行四边形,
,,
,
四边形是平行四边形.
又∵,
平行四边形是菱形.
20.(1)见解析
(2)的半径为10
【分析】(1)先证明四边形是平行四边形,得到,连接,,,三线合一结合平行线的性质,推出,即可得证;
(2)圆周角定理推出,解直角三角形求出圆的半径即可.
【详解】(1)证明:,分别是,的中点,
是的中位线,
,.
,
,
,
四边形是平行四边形,
.
如图,连接,,,
,
,即是的垂直平分线.
,
点在的垂直平分线上,即点,,共线.
,
,
又是的半径,
与相切.
(2)解:,,
,.
,
.
在中,,
,解之,得.
,
的半径为10.
【点睛】本题考查三角形的中位线定理,平行四边形的判定和性质,圆周角定理,切线的判定,解直角三角形,熟练掌握相关知识点,是解题的关键.
21.(1);(2)①理由见解析;②
【分析】本题考查解直角三角形的应用.把所给的角度整理到直角三角形中并进行解答是解决本题的关键.
(1)作于点N,延长交于点M,利用的正弦值和余弦值可得和的长度,进而可得的长度,那么根据的正切值可得的长度,那么的长度即为的长度减去的长度;
(2)①利用的正弦值和余弦值可得和的长度,进而可得的长度,那么根据的正切值可得的长度,那么的长度即为NE的长度减去的长度;
②设点A移动到了点,易得进而求得的长度,取的长度,减去的长度,即为固定器下降的距离.
【详解】解:(1)作于点N,延长交于点M,则,
∵爸爸身高是,此时水流正好喷在爸爸的“舒适喷淋点”C处,
∴,
∵
∴,
∵,
∴,
∴,
∴,
∴,
∴.
答:点A到地面的距离约为;
(2)①当时,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵小明的身高是,
∴小明的舒适距离,
∵,
∴水流无法喷在小明的“舒适喷淋点”处;
②设点A移动到了点,此时在小明的“舒适喷淋点”,
∴,
由题意得:,
∴,
∴.
答:固定器下降的距离约为.
22.(1)4,6,7
(2)见解析
(3)见解析,正方形的面积为8.
【分析】本题考查了正方形的性质,概率公式,七巧板,三角形的面积,熟练掌握七巧板是解题的关键.
(1)先计算出各个图块的面积,可得出答案;
(2)根据题意用七巧板拼成的一个类似“拱桥”图形即可;
(3)依据题意,在图2中画出拼接后的示意图,再计算出面积即可.
【详解】(1)解:正方形网格的边长为1,则面积为2的图形块有
图形块1,2的面积为:,
图形块3的面积为:,
图形块4的面积为:,
图形块5的面积为:,
图形块6的面积为:,
图形块7的面积为:,
面积为2的图形块有4,6,7,
故答案为:4,6,7;
(2)解:如图所示,
(3)解:如图所示,
正方形的面积为8.
23.(1)=;(2)108;(3)平方米.
【分析】(1)由平行线的性质,根据同底等高的两三角形面积相等作答;
(2)长不变,只要边上的高最大,面积最大;由图知当C是优弧的中点时,边上的高最大,面积最大,求得优弧的中点到的距离就可求得最大面积;
(3)过C作交的延长线于F,得,先证得四边形的面积的面积;根据得点F在以为边向外作的等边的外接圆上,受解决(2)的启发得,当F运动到点G时,的面积最大,即四边形的面积最大.最后计算出的面积即是四边形的面积最大值.
【详解】解:(1)如图①所示,分别过A、B两点向直线b作垂线,垂足为M、N,
∵
∴,
∴四边形是矩形,
∴,
∴
又,
∴;
故答案为:=;
(2)如图②,取优弧的中点记为,过作的垂线,垂足为D,
由垂径定理知过点O,且.
过点C作的平行线,
当直线向上平移时,与的距离增大,即的边上的高增大,
∴当CE运动到最高点C时,的边上的高最大.
又为定值,
∴当C运动到时,的面积最大,
连接,
,的直径为20,
,
在中,.
.
的面积为.
面积的最大值为108.
(3)如图,过点C作交的延长线于F.
.
.
,
四边形是平行四边形.
.
,
.
.
又由(1)的结论知,
.
所以只需求得最大值即得的最大值.
以AC为边向外作等边,再作等边的外接圆,过点G作于点J.如图,
,
点F在的外接圆上.
由第(2)问的解决知,当点F运动到点G时,.
在中,(米),
(米),
(米),
(平方米).
四边形面积的最大值为平方米.
【点睛】本题考查了三角形等积变形、定角对定边的三角形的面积最大值、等边三角形及其外接圆、平行四边形的判定和性质等考点,熟练掌握相关知识并能综合应用是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
