第二章 相交线与平行线 复习课 导学案(含答案) 北师大版 数学七年级下册(2024)
文档属性
| 名称 | 第二章 相交线与平行线 复习课 导学案(含答案) 北师大版 数学七年级下册(2024) |
|
|
| 格式 | docx | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 00:00:00 | ||
图片预览

文档简介
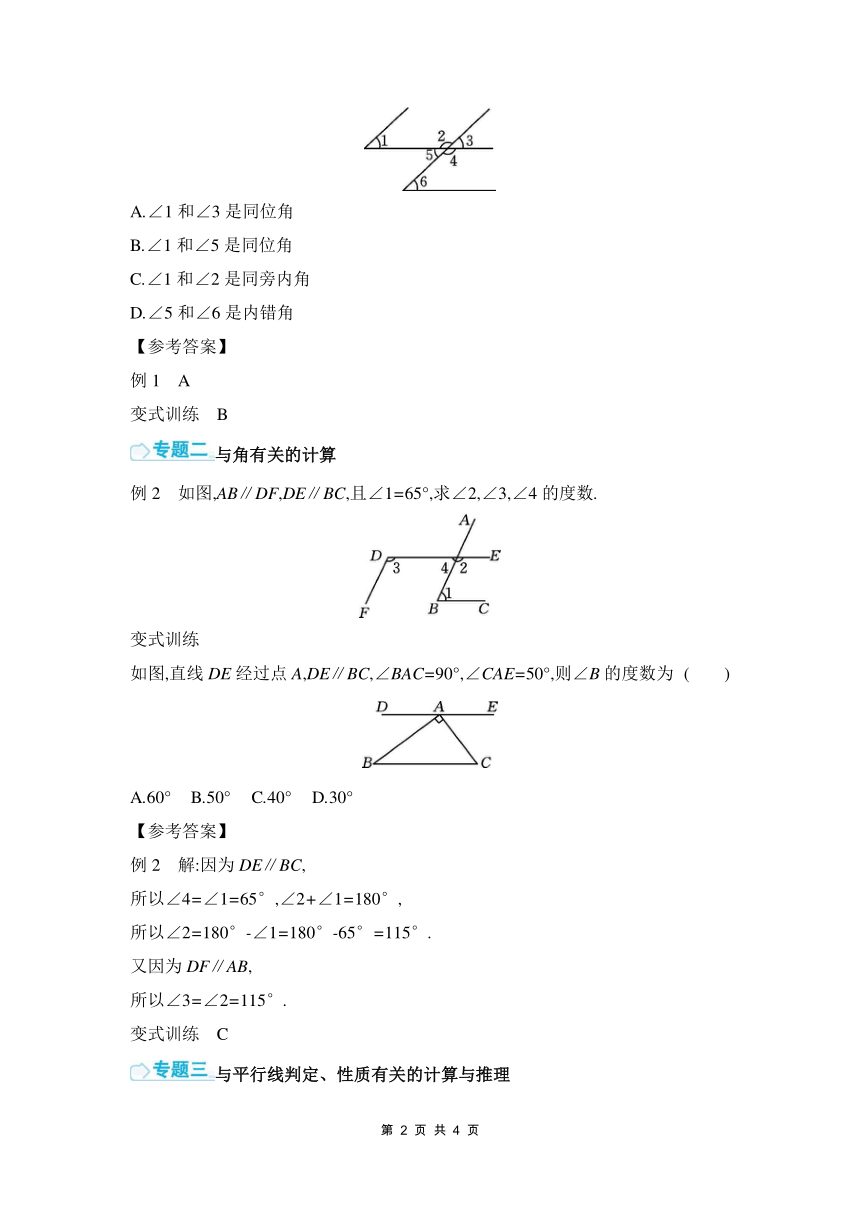
第二章 相交线与平行线 复习课
【复习目标】
1.加深对两条直线之间的位置关系的理解.
2.加深对对顶角、余角、补角、同位角、内错角、同旁内角等相关概念及性质的理解.
3.加深平行线的判定与性质的理解,并能灵活运用平行线的判定与性质解决实际问题.
【重点】
梳理本章的各个知识点.
【体系构建】
【专题复习】
与角有关的概念与识别
例1 如图,AB,CD被DE所截,则∠D的同位角是 ( )
A.∠1 B.∠2 C.∠3 D.∠4
变式训练
如图,下列说法错误的是 ( )
A.∠1和∠3是同位角
B.∠1和∠5是同位角
C.∠1和∠2是同旁内角
D.∠5和∠6是内错角
【参考答案】
例1 A
变式训练 B
与角有关的计算
例2 如图,AB∥DF,DE∥BC,且∠1=65°,求∠2,∠3,∠4的度数.
变式训练
如图,直线DE经过点A,DE∥BC,∠BAC=90°,∠CAE=50°,则∠B的度数为 ( )
A.60° B.50° C.40° D.30°
【参考答案】
例2 解:因为DE∥BC,
所以∠4=∠1=65°,∠2+∠1=180°,
所以∠2=180°-∠1=180°-65°=115°.
又因为DF∥AB,
所以∠3=∠2=115°.
变式训练 C
与平行线判定、性质有关的计算与推理
例3 如图,已知点E在BD上,EA平分∠BEF,EC平分∠DEF.
(1)试说明:AE⊥EC.
(2)当∠1=∠A,∠4=∠C时,AB与CD平行吗 为什么
变式训练
如图,根据条件完成填空.
①因为∠1= (已知),
所以AB∥CE( ).
②因为∠2= (已知),
所以CD∥BF( ).
③因为∠1+∠5=180°(已知),
所以CE∥ ( ).
④因为∠4+∠5=180°(已知),
所以 ∥ .
【参考答案】
例3 解:(1)因为EA平分∠BEF,EC平分∠DEF,
所以∠2=∠1=∠BEF,∠3=∠4=∠DEF.
因为∠BEF+∠DEF=180°,
所以∠2+∠3=(∠BEF+∠DEF)=90°,
所以AE⊥EC.
(2)AB∥CD.
理由如下:由(1)得∠2=∠1,∠3=∠4.
因为∠1=∠A,∠4=∠C,
所以∠A=∠2,∠3=∠C,
所以AB∥EF,EF∥CD,所以AB∥CD.
变式训练
①∠2 内错角相等,两直线平行
②∠4 同位角相等,两直线平行
③AB 同旁内角互补,两直线平行
④CD BF
平行线判定与性质在生活中的应用
例4如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从点E射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,且∠ODE=∠ADC,则∠DEB的度数是 ( )
A.35° B.70°
C.110° D.120°
变式训练
如图1,汽车前灯的反光装置相当于凹面镜,有了它,射出的光可看作平行光.现对此进行逆向分析,如图2,两条平行光线l1,l3通过凹面镜反射后的反射光线会聚于焦点F,l2是过焦点F的一条辅助线,根据图中信息,下列判断错误的是 ( )
A.l1∥l3 B.l1∥l2
C.l2∥l3 D.∠1=45°
【参考答案】
例4 B
变式训练 D
【复习目标】
1.加深对两条直线之间的位置关系的理解.
2.加深对对顶角、余角、补角、同位角、内错角、同旁内角等相关概念及性质的理解.
3.加深平行线的判定与性质的理解,并能灵活运用平行线的判定与性质解决实际问题.
【重点】
梳理本章的各个知识点.
【体系构建】
【专题复习】
与角有关的概念与识别
例1 如图,AB,CD被DE所截,则∠D的同位角是 ( )
A.∠1 B.∠2 C.∠3 D.∠4
变式训练
如图,下列说法错误的是 ( )
A.∠1和∠3是同位角
B.∠1和∠5是同位角
C.∠1和∠2是同旁内角
D.∠5和∠6是内错角
【参考答案】
例1 A
变式训练 B
与角有关的计算
例2 如图,AB∥DF,DE∥BC,且∠1=65°,求∠2,∠3,∠4的度数.
变式训练
如图,直线DE经过点A,DE∥BC,∠BAC=90°,∠CAE=50°,则∠B的度数为 ( )
A.60° B.50° C.40° D.30°
【参考答案】
例2 解:因为DE∥BC,
所以∠4=∠1=65°,∠2+∠1=180°,
所以∠2=180°-∠1=180°-65°=115°.
又因为DF∥AB,
所以∠3=∠2=115°.
变式训练 C
与平行线判定、性质有关的计算与推理
例3 如图,已知点E在BD上,EA平分∠BEF,EC平分∠DEF.
(1)试说明:AE⊥EC.
(2)当∠1=∠A,∠4=∠C时,AB与CD平行吗 为什么
变式训练
如图,根据条件完成填空.
①因为∠1= (已知),
所以AB∥CE( ).
②因为∠2= (已知),
所以CD∥BF( ).
③因为∠1+∠5=180°(已知),
所以CE∥ ( ).
④因为∠4+∠5=180°(已知),
所以 ∥ .
【参考答案】
例3 解:(1)因为EA平分∠BEF,EC平分∠DEF,
所以∠2=∠1=∠BEF,∠3=∠4=∠DEF.
因为∠BEF+∠DEF=180°,
所以∠2+∠3=(∠BEF+∠DEF)=90°,
所以AE⊥EC.
(2)AB∥CD.
理由如下:由(1)得∠2=∠1,∠3=∠4.
因为∠1=∠A,∠4=∠C,
所以∠A=∠2,∠3=∠C,
所以AB∥EF,EF∥CD,所以AB∥CD.
变式训练
①∠2 内错角相等,两直线平行
②∠4 同位角相等,两直线平行
③AB 同旁内角互补,两直线平行
④CD BF
平行线判定与性质在生活中的应用
例4如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从点E射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,且∠ODE=∠ADC,则∠DEB的度数是 ( )
A.35° B.70°
C.110° D.120°
变式训练
如图1,汽车前灯的反光装置相当于凹面镜,有了它,射出的光可看作平行光.现对此进行逆向分析,如图2,两条平行光线l1,l3通过凹面镜反射后的反射光线会聚于焦点F,l2是过焦点F的一条辅助线,根据图中信息,下列判断错误的是 ( )
A.l1∥l3 B.l1∥l2
C.l2∥l3 D.∠1=45°
【参考答案】
例4 B
变式训练 D
同课章节目录
