4.1 第1课时 三角形及内角和 导学案(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 4.1 第1课时 三角形及内角和 导学案(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 136.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 00:00:00 | ||
图片预览



文档简介
4.1 第1课时 三角形及内角和
【素养目标】
1.理解三角形概念及其基本要素.
2.探索并掌握三角形的内角和是180°和直角三角形两锐角互余定理,并会用三角形内角和定理进行角度的计算.
3.掌握锐角三角形、直角三角形、钝角三角形的概念,并会按角将三角形进行分类.
【重点】
探索并掌握三角形的内角和是180°,并会用三角形内角和定理进行角度的计算.
【自主预习】
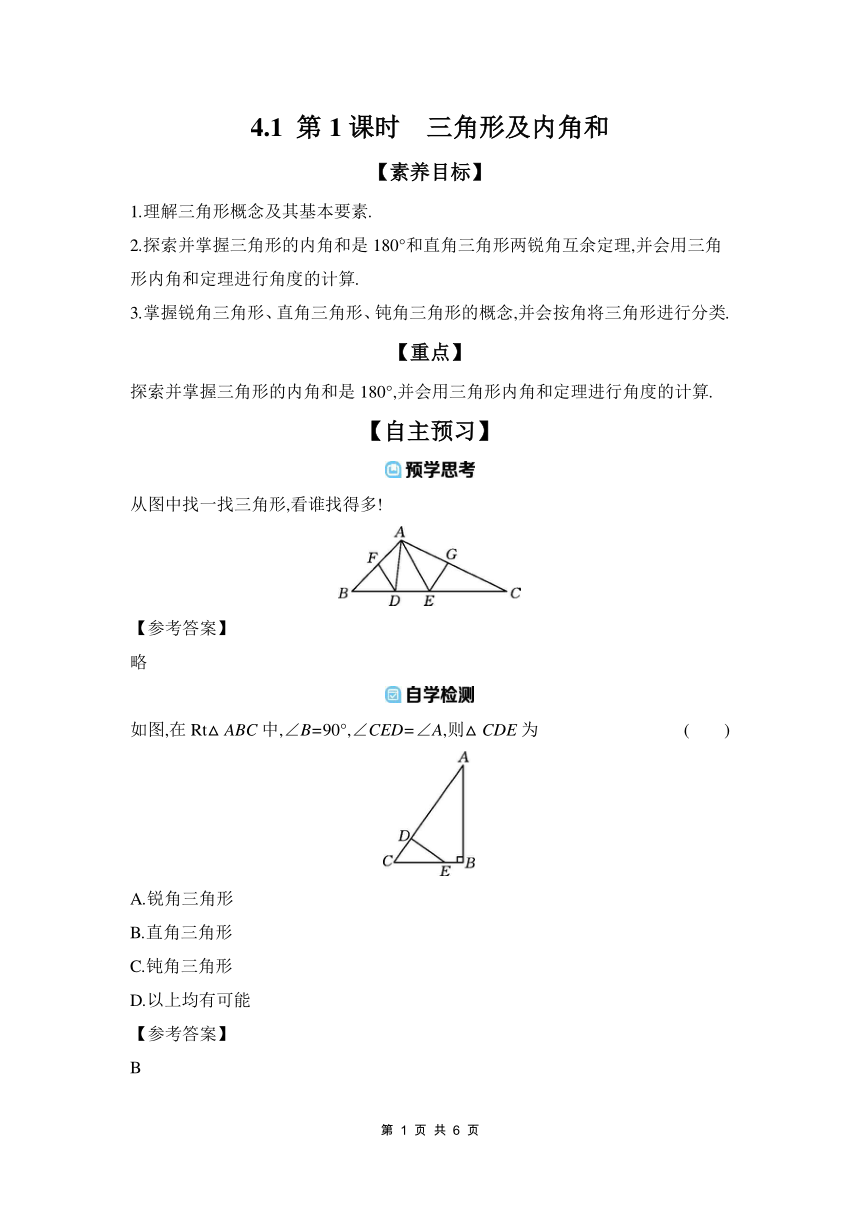
从图中找一找三角形,看谁找得多!
【参考答案】
略
如图,在Rt△ABC中,∠B=90°,∠CED=∠A,则△CDE为 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上均有可能
【参考答案】
B
【合作探究】
三角形的基本概念
阅读课本第85页“观察·交流”之前的内容,回答下列问题.
观察如图所示的图形,回答下列问题:
(1)图中有三个顶点,分别是 ,顶点通常用 表示.
(2)图中有三条线段,分别是 ,即为该图形的三条边长,有时也可用一个 表示.
(3)图中有三个角,分别是 ,即为该图形的三个内角.
【参考答案】
(1)点A,B,C 大写字母
(2)AB,BC,AC 小写字母
(3)∠A,∠B,∠C
由 所组成的图形叫作三角形.“三角形”可以用符号“ ”表示,若三角形的三个顶点是A,B,C,则该三角形记作 .
【参考答案】
不在同一直线上的三条线段首尾顺次相接 △ △ABC
三角形的内角和定理
阅读课本第85页“观察·交流”的内容,回答下列问题.
如图,过点A作直线DE∥BC,由平行线的性质,可得∠DAB= ,∠EAC= ,故∠BAC+∠DAB+∠EAC=∠BAC+ + =180°.
【参考答案】
∠B ∠C ∠B ∠C
三角形三个内角的和等于180°.
如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为 ( )
A.65° B.70° C.75° D.85°
【参考答案】
B
三角形的分类(按角分类)
阅读课本第86页“思考·交流”的内容,回答下列问题.
思考:由于三角形三个内角的和等于180°,那么三个内角中最大的角可能是什么角
【参考答案】
锐角、直角、钝角.
(1)三个内角都是锐角的三角形是 ,有一个内角是直角的三角形是 ,有一个内角是钝角的三角形是 ;
(2)通常用符号“ ”表示“直角三角形ABC”,把直角所对的边称为直角三角形的 ,夹直角的两条边称为 ;
(3)三角形的三个内角和等于 ,直角三角形中有一个直角,除这个直角外,两个锐角的和等于 ,即这两个锐角 .
【参考答案】
(1)锐角三角形 直角三角形 钝角三角形
(2)Rt△ABC 斜边 直角边
(3)180° 90° 互余
图中的三角形被木板遮住了一部分,这个三角形是 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
【参考答案】
D
三角形内角和定理的应用
例1 在△ABC中,∠A∶∠B∶∠C=2∶2∶4,求∠A,∠B,∠C的度数.
变式训练
如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,则∠BPC的度数是 ( )
A.150° B.130°
C.120° D.100°
【参考答案】
例1 解:设每一份角为x°,则∠A=2x°,∠B=2x°,∠C=4x°.
由三角形内角和定理,可得
2x+2x+4x=180,
解得x=22.5,
2x=2×22.5=45,4x=4×22.5=90.
答:∠A为45°,∠B为45°,∠C为90°.
变式训练 B
三角形的分类
例2 观察下面的三角形,并把它们的标号填入相应的圈内.
【参考答案】
例2 解:锐角三角形:③④.
直角三角形:①⑤.
钝角三角形:②⑥.
【素养目标】
1.理解三角形概念及其基本要素.
2.探索并掌握三角形的内角和是180°和直角三角形两锐角互余定理,并会用三角形内角和定理进行角度的计算.
3.掌握锐角三角形、直角三角形、钝角三角形的概念,并会按角将三角形进行分类.
【重点】
探索并掌握三角形的内角和是180°,并会用三角形内角和定理进行角度的计算.
【自主预习】
从图中找一找三角形,看谁找得多!
【参考答案】
略
如图,在Rt△ABC中,∠B=90°,∠CED=∠A,则△CDE为 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上均有可能
【参考答案】
B
【合作探究】
三角形的基本概念
阅读课本第85页“观察·交流”之前的内容,回答下列问题.
观察如图所示的图形,回答下列问题:
(1)图中有三个顶点,分别是 ,顶点通常用 表示.
(2)图中有三条线段,分别是 ,即为该图形的三条边长,有时也可用一个 表示.
(3)图中有三个角,分别是 ,即为该图形的三个内角.
【参考答案】
(1)点A,B,C 大写字母
(2)AB,BC,AC 小写字母
(3)∠A,∠B,∠C
由 所组成的图形叫作三角形.“三角形”可以用符号“ ”表示,若三角形的三个顶点是A,B,C,则该三角形记作 .
【参考答案】
不在同一直线上的三条线段首尾顺次相接 △ △ABC
三角形的内角和定理
阅读课本第85页“观察·交流”的内容,回答下列问题.
如图,过点A作直线DE∥BC,由平行线的性质,可得∠DAB= ,∠EAC= ,故∠BAC+∠DAB+∠EAC=∠BAC+ + =180°.
【参考答案】
∠B ∠C ∠B ∠C
三角形三个内角的和等于180°.
如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为 ( )
A.65° B.70° C.75° D.85°
【参考答案】
B
三角形的分类(按角分类)
阅读课本第86页“思考·交流”的内容,回答下列问题.
思考:由于三角形三个内角的和等于180°,那么三个内角中最大的角可能是什么角
【参考答案】
锐角、直角、钝角.
(1)三个内角都是锐角的三角形是 ,有一个内角是直角的三角形是 ,有一个内角是钝角的三角形是 ;
(2)通常用符号“ ”表示“直角三角形ABC”,把直角所对的边称为直角三角形的 ,夹直角的两条边称为 ;
(3)三角形的三个内角和等于 ,直角三角形中有一个直角,除这个直角外,两个锐角的和等于 ,即这两个锐角 .
【参考答案】
(1)锐角三角形 直角三角形 钝角三角形
(2)Rt△ABC 斜边 直角边
(3)180° 90° 互余
图中的三角形被木板遮住了一部分,这个三角形是 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
【参考答案】
D
三角形内角和定理的应用
例1 在△ABC中,∠A∶∠B∶∠C=2∶2∶4,求∠A,∠B,∠C的度数.
变式训练
如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,则∠BPC的度数是 ( )
A.150° B.130°
C.120° D.100°
【参考答案】
例1 解:设每一份角为x°,则∠A=2x°,∠B=2x°,∠C=4x°.
由三角形内角和定理,可得
2x+2x+4x=180,
解得x=22.5,
2x=2×22.5=45,4x=4×22.5=90.
答:∠A为45°,∠B为45°,∠C为90°.
变式训练 B
三角形的分类
例2 观察下面的三角形,并把它们的标号填入相应的圈内.
【参考答案】
例2 解:锐角三角形:③④.
直角三角形:①⑤.
钝角三角形:②⑥.
同课章节目录
