4.3 第2课时 角边角与角角边 导学案(含答案)2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 4.3 第2课时 角边角与角角边 导学案(含答案)2024-2025学年北师大版(2024)七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 117.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 00:00:00 | ||
图片预览

文档简介
4.3 第2课时 角边角与角角边
【素养目标】
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.会运用角边角定理尺规作三角形全等于已知三角形.
3.学会运用“角边角”“角角边”判定方法进行简单的说理.
【重点】
三角形全等的条件ASA,AAS的探索.
【自主预习】
如果已知一个三角形的两角及一边,那么有几种可能的情况呢 每种情况下得到的三角形都全等吗
【参考答案】
有两种可能的情况,两角夹边(ASA),两角对边(AAS),都可以得到两个三角形全等.
(条件开放)如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).
【参考答案】
答案不唯一,如∠B=∠C等
【合作探究】
判定两个三角形全等的基本事实“角边角”
阅读课本第101页“尝试·思考”的内容,回答下列问题.
1.若已知三角形的两个内角和其中一条边长,则边长可能是两角之间的 边,也可能是其中一个角的 .
2.若已知某三角形的两个角分别为30°,45°,两个角之间的夹边为2 cm,尝试着用量角器和有刻度的尺子画一画,比一比大家画的三角形是一样的吗
【参考答案】
1.夹 对边
2.作图略,大家所画三角形一致.
两角和它们的 分别相等的两个三角形全等,简写为“ ”或“ ”.
【参考答案】
夹边 角边角 ASA
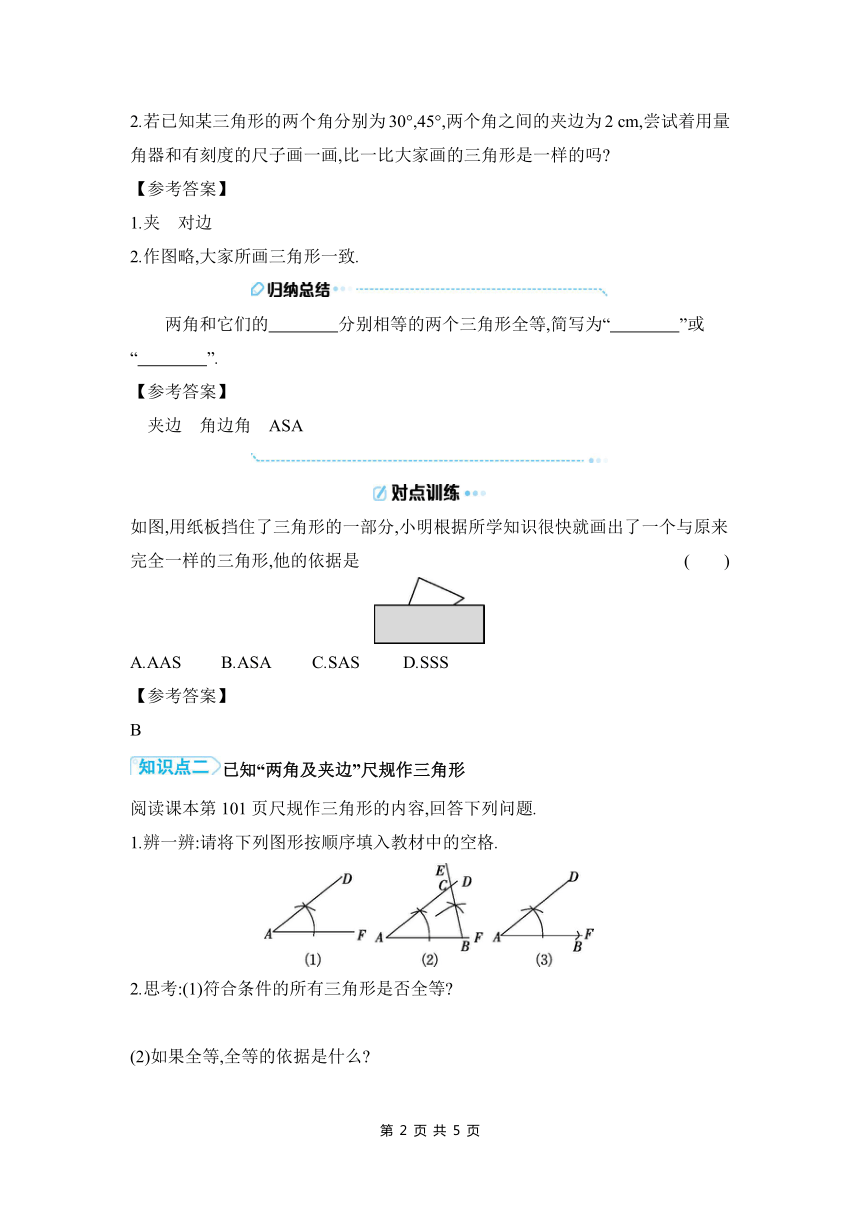
如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是 ( )
A.AAS B.ASA C.SAS D.SSS
【参考答案】
B
已知“两角及夹边”尺规作三角形
阅读课本第101页尺规作三角形的内容,回答下列问题.
1.辨一辨:请将下列图形按顺序填入教材中的空格.
2.思考:(1)符合条件的所有三角形是否全等
(2)如果全等,全等的依据是什么
【参考答案】
1.(1)(3)(2).
2.(1)全等. (2)ASA.
如图,这是作△ABC的作图痕迹,则此作图的已知条件为
( )
A.已知两角及夹边
B.已知三边
C.已知两边及夹角
D.已知两边及一边夹角
【参考答案】
A
判定两三角形全等的基本事实“角角边”
阅读课本第102页“思考·交流”的内容,回答下列问题:
若已知某三角形的两角分别为60°,45°,45°角所对的边为2 cm,尝试着用量角器和有刻度的尺子画一画,比一比大家画的三角形是一样的吗
两角分别相等且其中一组等角的 相等的两个三角形全等,简称“ ”或“ ”.
【参考答案】
对边 角角边 AAS
如图,∠B=∠C,∠1=∠2,直接判定△ABD≌△ACD的理由是 ( )
A.AAS B.SSS
C.ASA D.SAS
【参考答案】
A
“角边角”定理的应用
例1 如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.
【参考答案】
例1 解:因为AD∥BC,BE∥DF,
所以∠A=∠C,∠DFE=∠BEC.
因为AE=CF,所以AE+EF=CF+EF,
即AF=CE.
在△ADF和△CBE中,
所以△ADF≌△CBE(ASA).
“角角边”定理的应用
例2 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E.AD与BE交于点F,若BF=AC,试说明:△ADC≌△BDF.
变式训练
如图,已知AB与CD相交于点O,∠A=∠D,CO=BO,你能说明△AOC≌△DOB吗
【参考答案】
例2 解:因为AD⊥BC,BE⊥AC,
所以∠ADC=∠BDF=∠BEA=90°.
因为∠AFE=∠BFD,∠DAC+∠AEF+∠AFE=180°,∠BDF+∠BFD+∠DBF=180°,所以∠DAC=∠DBF.
在△ADC和△BDF中,
所以△ADC≌△BDF(AAS).
变式训练
解:能.在△AOC和△DOB中,因为∠A=∠D,CO=BO,∠AOC=∠DOB(对顶角相等),
所以△AOC≌△DOB(AAS).
【素养目标】
1.掌握三角形全等的“角边角”“角角边”判定方法.
2.会运用角边角定理尺规作三角形全等于已知三角形.
3.学会运用“角边角”“角角边”判定方法进行简单的说理.
【重点】
三角形全等的条件ASA,AAS的探索.
【自主预习】
如果已知一个三角形的两角及一边,那么有几种可能的情况呢 每种情况下得到的三角形都全等吗
【参考答案】
有两种可能的情况,两角夹边(ASA),两角对边(AAS),都可以得到两个三角形全等.
(条件开放)如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).
【参考答案】
答案不唯一,如∠B=∠C等
【合作探究】
判定两个三角形全等的基本事实“角边角”
阅读课本第101页“尝试·思考”的内容,回答下列问题.
1.若已知三角形的两个内角和其中一条边长,则边长可能是两角之间的 边,也可能是其中一个角的 .
2.若已知某三角形的两个角分别为30°,45°,两个角之间的夹边为2 cm,尝试着用量角器和有刻度的尺子画一画,比一比大家画的三角形是一样的吗
【参考答案】
1.夹 对边
2.作图略,大家所画三角形一致.
两角和它们的 分别相等的两个三角形全等,简写为“ ”或“ ”.
【参考答案】
夹边 角边角 ASA
如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是 ( )
A.AAS B.ASA C.SAS D.SSS
【参考答案】
B
已知“两角及夹边”尺规作三角形
阅读课本第101页尺规作三角形的内容,回答下列问题.
1.辨一辨:请将下列图形按顺序填入教材中的空格.
2.思考:(1)符合条件的所有三角形是否全等
(2)如果全等,全等的依据是什么
【参考答案】
1.(1)(3)(2).
2.(1)全等. (2)ASA.
如图,这是作△ABC的作图痕迹,则此作图的已知条件为
( )
A.已知两角及夹边
B.已知三边
C.已知两边及夹角
D.已知两边及一边夹角
【参考答案】
A
判定两三角形全等的基本事实“角角边”
阅读课本第102页“思考·交流”的内容,回答下列问题:
若已知某三角形的两角分别为60°,45°,45°角所对的边为2 cm,尝试着用量角器和有刻度的尺子画一画,比一比大家画的三角形是一样的吗
两角分别相等且其中一组等角的 相等的两个三角形全等,简称“ ”或“ ”.
【参考答案】
对边 角角边 AAS
如图,∠B=∠C,∠1=∠2,直接判定△ABD≌△ACD的理由是 ( )
A.AAS B.SSS
C.ASA D.SAS
【参考答案】
A
“角边角”定理的应用
例1 如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.
【参考答案】
例1 解:因为AD∥BC,BE∥DF,
所以∠A=∠C,∠DFE=∠BEC.
因为AE=CF,所以AE+EF=CF+EF,
即AF=CE.
在△ADF和△CBE中,
所以△ADF≌△CBE(ASA).
“角角边”定理的应用
例2 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E.AD与BE交于点F,若BF=AC,试说明:△ADC≌△BDF.
变式训练
如图,已知AB与CD相交于点O,∠A=∠D,CO=BO,你能说明△AOC≌△DOB吗
【参考答案】
例2 解:因为AD⊥BC,BE⊥AC,
所以∠ADC=∠BDF=∠BEA=90°.
因为∠AFE=∠BFD,∠DAC+∠AEF+∠AFE=180°,∠BDF+∠BFD+∠DBF=180°,所以∠DAC=∠DBF.
在△ADC和△BDF中,
所以△ADC≌△BDF(AAS).
变式训练
解:能.在△AOC和△DOB中,因为∠A=∠D,CO=BO,∠AOC=∠DOB(对顶角相等),
所以△AOC≌△DOB(AAS).
同课章节目录
