问题解决策略:特殊化 导学案(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 问题解决策略:特殊化 导学案(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 00:00:00 | ||
图片预览


文档简介
问题解决策略:特殊化
【素养目标】
1.灵活运用判定三角形全等的条件解决实际问题.
2.了解运用特殊情况解决一般情况的方法.
【重点】
灵活运用判定三角形全等的条件解决实际问题.
【自主预习】
如图,点A,O,B在同一直线上,OD,OE分别是∠AOC与∠BOC的角平分线,试探究OD与OE的位置关系.
1.思考:(1)当∠AOC=90°时,∠BOC= ,∠AOD=∠DOC=∠COE=∠BOE= ,∠DOE= .
(2)当∠AOC=40°时,∠BOC= ,∠AOD=∠DOC= ,∠COE=∠BOE
= ,∠DOE= .
2.∠AOC再取几个特殊值算一算.
3.猜想:OD OE,试说明理由.
【参考答案】
1.(1)90° 45° 90°
(2)140° 20° 70° 90°
3.⊥
如图,∠ABC与∠ACB的角平分线交于O点,试探究∠BOC与∠A的大小关系,对照预学思考中由特殊到一般的思路,∠A取特殊值试一试.
【合作探究】
特殊化策略
阅读课本第113-114页中的内容,回答下列问题:
1.图4-34中,正方形EFGH与正方形ABCD的重叠部分是什么图形
2.图4-35与图4-36中,两个正方形的重叠部分是哪个图形 它们的面积为什么是正方形ABCD面积的
3.图4-37中,BE= ,∠BEC=∠FEH= ,∠EBC=∠ECB= ,所以,∠NEC= ,所以△NEC≌△MEB.
【参考答案】
1.四边形ENCM.
2.图4-35中重叠部分是△BEC,图4-36中重叠部分是正方形MENB,如图,可知它们的面积是正方形ABCD面积的.
3.EC 90° 45° ∠MEB
在上面的问题中,正方形EFGH的位置是 ,所求重叠部分的面积有很多情形,因此,小明尝试从 入手,并借助特殊情形的经验解决了一般情形下的问题.因为某些因素(如形状、位置或数值等)不确定,使得问题有多种情形时,可以限制这个引起变化的因素,考虑最为特殊的情形,采用从 入手的策略解决问题.
【参考答案】
变化的 特殊情形 特殊情形
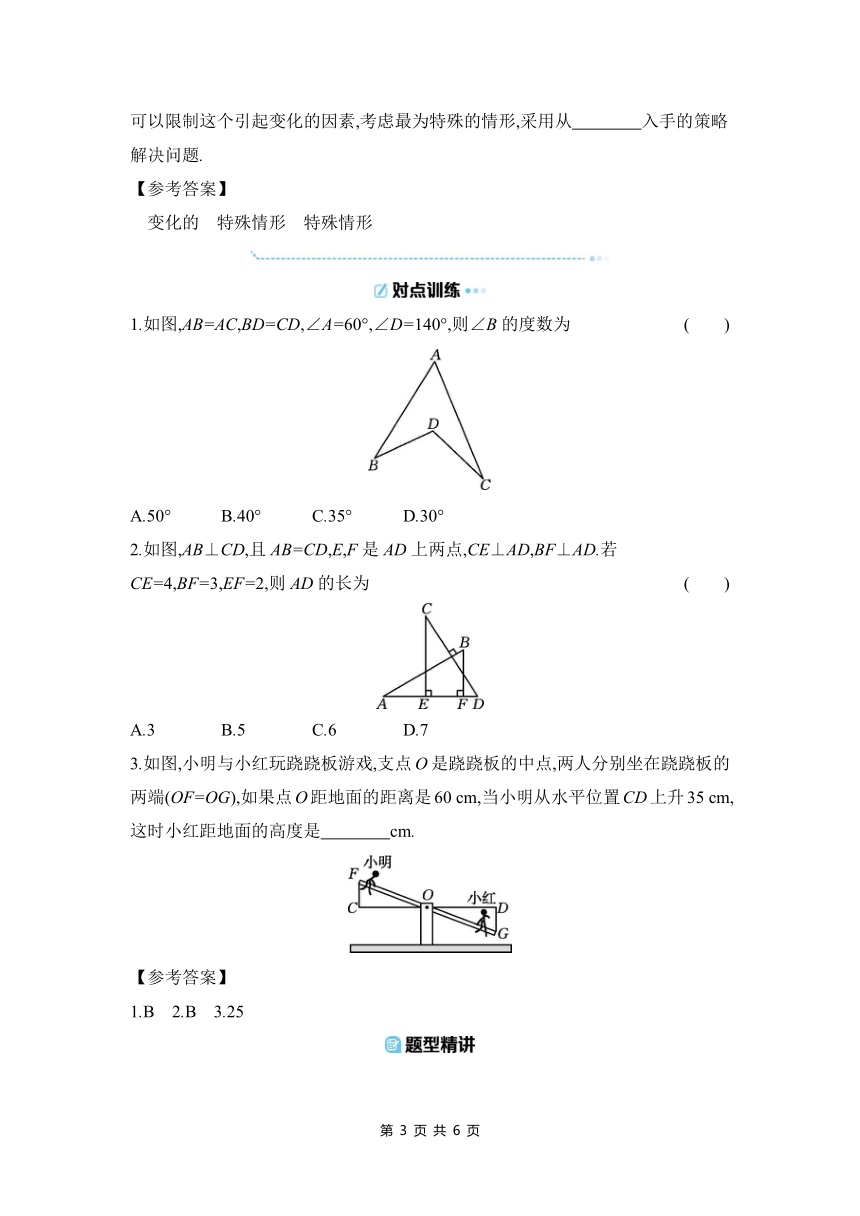
1.如图,AB=AC,BD=CD,∠A=60°,∠D=140°,则∠B的度数为 ( )
A.50° B.40° C.35° D.30°
2.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为 ( )
A.3 B.5 C.6 D.7
3.如图,小明与小红玩跷跷板游戏,支点O是跷跷板的中点,两人分别坐在跷跷板的两端(OF=OG),如果点O距地面的距离是60 cm,当小明从水平位置CD上升35 cm,这时小红距地面的高度是 cm.
【参考答案】
1.B 2.B 3.25
例 在△ABC中,∠ACB=90°,AC=BC,过点C作直线MN,AM⊥MN于点M,BN⊥MN于点N.
(1)若MN在△ABC外(如图1),试说明MN=AM+BN.
(2)若MN与线段AB相交(如图2),且AM=2.6,BN=1.1,则MN= .
变式训练
在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图1,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是BE= ,∠BDC的度数为 .
【类比探究】如图2,若∠BAC=120°,延长BE,交FC的延长线于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【参考答案】
例 解:(1)因为AM⊥MN,BN⊥MN,
所以∠AMC=∠CNB=90°.
因为∠ACB=90°,∠AMC=90°,
所以∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
所以∠MAC=∠NCB.
在△AMC和△CNB中,
所以△AMC≌△CNB(AAS),
所以AM=CN,MC=NB.
因为MN=NC+CM,
所以MN=AM+BN.
(2)1.5.
提示:因为AM⊥MN于点M,BN⊥MN于点N,
所以∠AMC=∠CNB=90°,
所以∠MAC+∠ACM=90°.
因为∠ACB=90°,
所以∠ACM+∠NCB=90°,
所以∠MAC=∠NCB.
在△ACM和△CBN中,
所以△ACM≌△CBN(AAS),
所以AM=CN=2.6,CM=BN=1.1,
所以MN=CN-CM=2.6-1.1=1.5.
变式训练
【发现问题】CF 30°
解:BE=CF,∠BDC=60°.
理由:因为∠BAC=∠EAF=120°,
所以∠BAC-∠EAC=∠EAF-∠EAC,
即∠BAE=∠CAF.
在△ABE和△ACF中,
所以△ABE≌△ACF(SAS),
所以BE=CF,∠AEB=∠AFC.
因为∠EAF=120°,AE=AF,
所以∠AEF=∠AFE=30°,
所以∠FED=180°-∠AEB-30°=150°-∠AEB,
∠EFD=∠AFC-30°=∠AEB-30°,所以∠BDC=180°-∠FED-∠EFD=180°-(150°-∠AEB)-(∠AEB-30°)=60°.
【素养目标】
1.灵活运用判定三角形全等的条件解决实际问题.
2.了解运用特殊情况解决一般情况的方法.
【重点】
灵活运用判定三角形全等的条件解决实际问题.
【自主预习】
如图,点A,O,B在同一直线上,OD,OE分别是∠AOC与∠BOC的角平分线,试探究OD与OE的位置关系.
1.思考:(1)当∠AOC=90°时,∠BOC= ,∠AOD=∠DOC=∠COE=∠BOE= ,∠DOE= .
(2)当∠AOC=40°时,∠BOC= ,∠AOD=∠DOC= ,∠COE=∠BOE
= ,∠DOE= .
2.∠AOC再取几个特殊值算一算.
3.猜想:OD OE,试说明理由.
【参考答案】
1.(1)90° 45° 90°
(2)140° 20° 70° 90°
3.⊥
如图,∠ABC与∠ACB的角平分线交于O点,试探究∠BOC与∠A的大小关系,对照预学思考中由特殊到一般的思路,∠A取特殊值试一试.
【合作探究】
特殊化策略
阅读课本第113-114页中的内容,回答下列问题:
1.图4-34中,正方形EFGH与正方形ABCD的重叠部分是什么图形
2.图4-35与图4-36中,两个正方形的重叠部分是哪个图形 它们的面积为什么是正方形ABCD面积的
3.图4-37中,BE= ,∠BEC=∠FEH= ,∠EBC=∠ECB= ,所以,∠NEC= ,所以△NEC≌△MEB.
【参考答案】
1.四边形ENCM.
2.图4-35中重叠部分是△BEC,图4-36中重叠部分是正方形MENB,如图,可知它们的面积是正方形ABCD面积的.
3.EC 90° 45° ∠MEB
在上面的问题中,正方形EFGH的位置是 ,所求重叠部分的面积有很多情形,因此,小明尝试从 入手,并借助特殊情形的经验解决了一般情形下的问题.因为某些因素(如形状、位置或数值等)不确定,使得问题有多种情形时,可以限制这个引起变化的因素,考虑最为特殊的情形,采用从 入手的策略解决问题.
【参考答案】
变化的 特殊情形 特殊情形
1.如图,AB=AC,BD=CD,∠A=60°,∠D=140°,则∠B的度数为 ( )
A.50° B.40° C.35° D.30°
2.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为 ( )
A.3 B.5 C.6 D.7
3.如图,小明与小红玩跷跷板游戏,支点O是跷跷板的中点,两人分别坐在跷跷板的两端(OF=OG),如果点O距地面的距离是60 cm,当小明从水平位置CD上升35 cm,这时小红距地面的高度是 cm.
【参考答案】
1.B 2.B 3.25
例 在△ABC中,∠ACB=90°,AC=BC,过点C作直线MN,AM⊥MN于点M,BN⊥MN于点N.
(1)若MN在△ABC外(如图1),试说明MN=AM+BN.
(2)若MN与线段AB相交(如图2),且AM=2.6,BN=1.1,则MN= .
变式训练
在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图1,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是BE= ,∠BDC的度数为 .
【类比探究】如图2,若∠BAC=120°,延长BE,交FC的延长线于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【参考答案】
例 解:(1)因为AM⊥MN,BN⊥MN,
所以∠AMC=∠CNB=90°.
因为∠ACB=90°,∠AMC=90°,
所以∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
所以∠MAC=∠NCB.
在△AMC和△CNB中,
所以△AMC≌△CNB(AAS),
所以AM=CN,MC=NB.
因为MN=NC+CM,
所以MN=AM+BN.
(2)1.5.
提示:因为AM⊥MN于点M,BN⊥MN于点N,
所以∠AMC=∠CNB=90°,
所以∠MAC+∠ACM=90°.
因为∠ACB=90°,
所以∠ACM+∠NCB=90°,
所以∠MAC=∠NCB.
在△ACM和△CBN中,
所以△ACM≌△CBN(AAS),
所以AM=CN=2.6,CM=BN=1.1,
所以MN=CN-CM=2.6-1.1=1.5.
变式训练
【发现问题】CF 30°
解:BE=CF,∠BDC=60°.
理由:因为∠BAC=∠EAF=120°,
所以∠BAC-∠EAC=∠EAF-∠EAC,
即∠BAE=∠CAF.
在△ABE和△ACF中,
所以△ABE≌△ACF(SAS),
所以BE=CF,∠AEB=∠AFC.
因为∠EAF=120°,AE=AF,
所以∠AEF=∠AFE=30°,
所以∠FED=180°-∠AEB-30°=150°-∠AEB,
∠EFD=∠AFC-30°=∠AEB-30°,所以∠BDC=180°-∠FED-∠EFD=180°-(150°-∠AEB)-(∠AEB-30°)=60°.
同课章节目录
