5.2 第2课时 线段的垂直平分线 导学案(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 5.2 第2课时 线段的垂直平分线 导学案(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 140.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 00:00:00 | ||
图片预览

文档简介
5.2 第2课时 线段的垂直平分线
【素养目标】
1.知道线段垂直平分线的定义.
2.知道并掌握线段垂直平分线性质,能利用线段垂直平分线的性质解决实际问题.
3.能利用尺规作图画出线段的垂直平分线.
【重点】
理解线段垂直平分线的有关性质.
【自主预习】
1.什么是轴对称图形 它的对称轴是什么
2.下面哪些图形是轴对称图形
【参考答案】
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
2.第一个和第三个图形是轴对称图形.
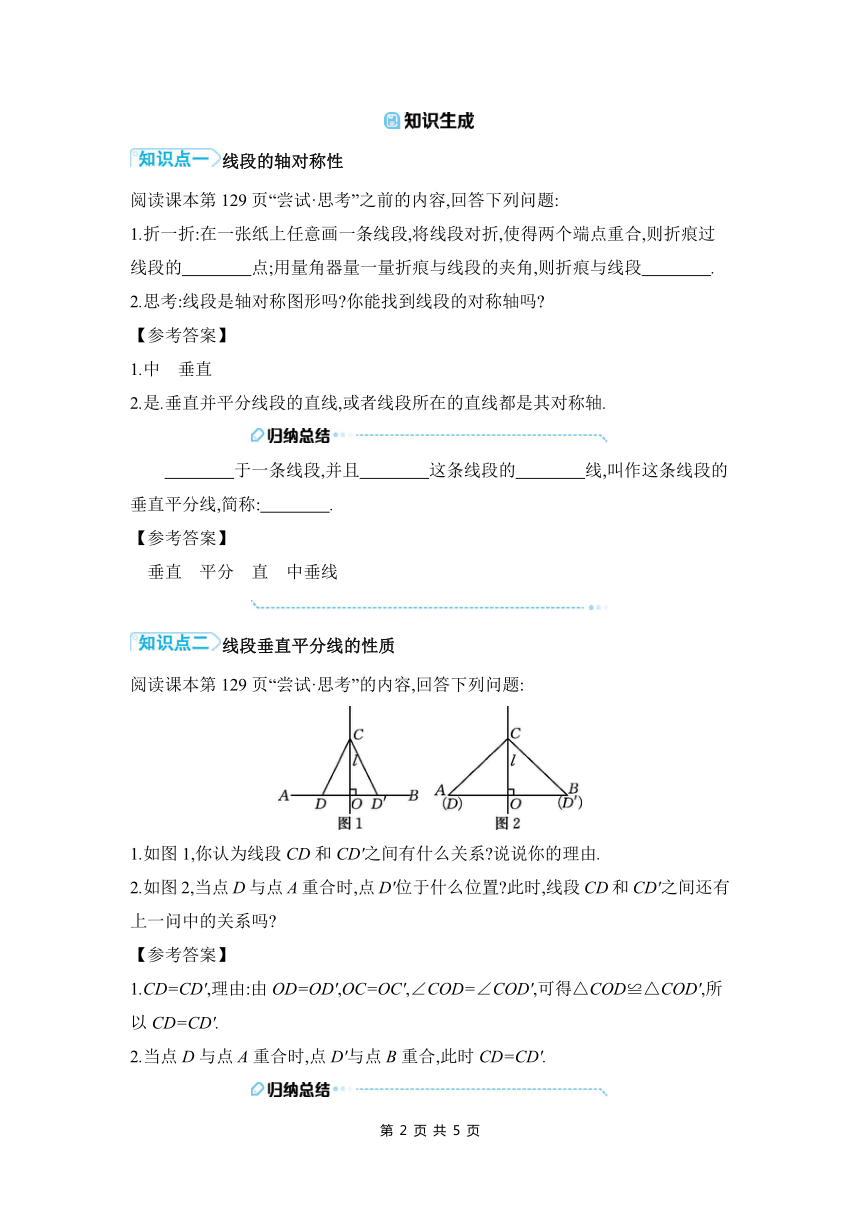
如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是 ( )
A.12 B.13 C.14 D.15
【参考答案】
B
【合作探究】
线段的轴对称性
阅读课本第129页“尝试·思考”之前的内容,回答下列问题:
1.折一折:在一张纸上任意画一条线段,将线段对折,使得两个端点重合,则折痕过线段的 点;用量角器量一量折痕与线段的夹角,则折痕与线段 .
2.思考:线段是轴对称图形吗 你能找到线段的对称轴吗
【参考答案】
1.中 垂直
2.是.垂直并平分线段的直线,或者线段所在的直线都是其对称轴.
于一条线段,并且 这条线段的 线,叫作这条线段的垂直平分线,简称: .
【参考答案】
垂直 平分 直 中垂线
线段垂直平分线的性质
阅读课本第129页“尝试·思考”的内容,回答下列问题:
1.如图1,你认为线段CD和CD'之间有什么关系 说说你的理由.
2.如图2,当点D与点A重合时,点D'位于什么位置 此时,线段CD和CD'之间还有上一问中的关系吗
【参考答案】
1.CD=CD',理由:由OD=OD',OC=OC',∠COD=∠COD',可得△COD≌△COD',所以CD=CD'.
2.当点D与点A重合时,点D'与点B重合,此时CD=CD'.
线段垂直平分线上的点到这条线段 的距离 .
【参考答案】
两个端点 相等
如图,在△ABC中,D,E分别是边AC,BC上的点,DE垂直平分AC,连接AE.若∠C=42°,∠BAC=85°,则∠BAE的度数为 ( )
A.43° B.42° C.45° D.53°
【参考答案】
A
用尺规作线段的垂直平分线
阅读课本第129页“思考·交流”“例2”和第130页“操作·思考”的内容,回答下列问题:
1.操作:图5-14中,用度量的方法找出线段AB的中点,用三角板过中点作直线MN⊥AB,在直线MN上取两点C,D,连接CA,CB,DA,DB.
2.思考:(1)CA与CB,DA与DB有何数量关系 如果只用尺规,该如何确定C,D的位置
(2)课本“例2”中,用圆规画弧可得AC BC,AD BD,△ACD △BCD( ),它们是成轴对称的图形吗 对称轴是哪条直线
(3)直线CD是线段AB的对称轴吗
(4)图5-16中如何在直线l上找A,B两点,使AP=BP
(5)参照例2中的作法画线段AB的垂直线平分线,线段AB的垂直平分线会经过点P吗
【参考答案】
2.(1)CA=CB,DA=DB,可以分别以点A,B为圆心,大于AB的长为半径画弧来确定.
(2)= = ≌ SSS 是,CD是对称轴.
(3)是.
(4)以点P为圆心,任意长度为半径画弧交直线l于A,B两点,则AP=BP.
(5)会.
用尺规作图作线段的垂直平分线时,要注意线段两侧都要构造弧的 .
【参考答案】
交点
线段垂直平分线性质的应用
例1 三条公路将A,B,C三个村庄连成一个如图所示的三角形区域,如果在这个区域内修建一个公园,要使公园到三个村庄的距离相等,那么这个公园应建的位置是△ABC的 ( )
A.三条高的交点
B.三边垂直平分线的交点
C.三条角平分线的交点
D.三条中线的交点
【参考答案】
交点
运用线段垂直平分线性质尺规作图
例2 如图,在△ABC中,以点A为圆心,AC的长为半径作圆弧交BC于点D,再分别以点B和点D为圆心,大于BD的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.若AB=9,AC=7,则△ADE的周长为 .
【参考答案】
例2 16
【素养目标】
1.知道线段垂直平分线的定义.
2.知道并掌握线段垂直平分线性质,能利用线段垂直平分线的性质解决实际问题.
3.能利用尺规作图画出线段的垂直平分线.
【重点】
理解线段垂直平分线的有关性质.
【自主预习】
1.什么是轴对称图形 它的对称轴是什么
2.下面哪些图形是轴对称图形
【参考答案】
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
2.第一个和第三个图形是轴对称图形.
如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是 ( )
A.12 B.13 C.14 D.15
【参考答案】
B
【合作探究】
线段的轴对称性
阅读课本第129页“尝试·思考”之前的内容,回答下列问题:
1.折一折:在一张纸上任意画一条线段,将线段对折,使得两个端点重合,则折痕过线段的 点;用量角器量一量折痕与线段的夹角,则折痕与线段 .
2.思考:线段是轴对称图形吗 你能找到线段的对称轴吗
【参考答案】
1.中 垂直
2.是.垂直并平分线段的直线,或者线段所在的直线都是其对称轴.
于一条线段,并且 这条线段的 线,叫作这条线段的垂直平分线,简称: .
【参考答案】
垂直 平分 直 中垂线
线段垂直平分线的性质
阅读课本第129页“尝试·思考”的内容,回答下列问题:
1.如图1,你认为线段CD和CD'之间有什么关系 说说你的理由.
2.如图2,当点D与点A重合时,点D'位于什么位置 此时,线段CD和CD'之间还有上一问中的关系吗
【参考答案】
1.CD=CD',理由:由OD=OD',OC=OC',∠COD=∠COD',可得△COD≌△COD',所以CD=CD'.
2.当点D与点A重合时,点D'与点B重合,此时CD=CD'.
线段垂直平分线上的点到这条线段 的距离 .
【参考答案】
两个端点 相等
如图,在△ABC中,D,E分别是边AC,BC上的点,DE垂直平分AC,连接AE.若∠C=42°,∠BAC=85°,则∠BAE的度数为 ( )
A.43° B.42° C.45° D.53°
【参考答案】
A
用尺规作线段的垂直平分线
阅读课本第129页“思考·交流”“例2”和第130页“操作·思考”的内容,回答下列问题:
1.操作:图5-14中,用度量的方法找出线段AB的中点,用三角板过中点作直线MN⊥AB,在直线MN上取两点C,D,连接CA,CB,DA,DB.
2.思考:(1)CA与CB,DA与DB有何数量关系 如果只用尺规,该如何确定C,D的位置
(2)课本“例2”中,用圆规画弧可得AC BC,AD BD,△ACD △BCD( ),它们是成轴对称的图形吗 对称轴是哪条直线
(3)直线CD是线段AB的对称轴吗
(4)图5-16中如何在直线l上找A,B两点,使AP=BP
(5)参照例2中的作法画线段AB的垂直线平分线,线段AB的垂直平分线会经过点P吗
【参考答案】
2.(1)CA=CB,DA=DB,可以分别以点A,B为圆心,大于AB的长为半径画弧来确定.
(2)= = ≌ SSS 是,CD是对称轴.
(3)是.
(4)以点P为圆心,任意长度为半径画弧交直线l于A,B两点,则AP=BP.
(5)会.
用尺规作图作线段的垂直平分线时,要注意线段两侧都要构造弧的 .
【参考答案】
交点
线段垂直平分线性质的应用
例1 三条公路将A,B,C三个村庄连成一个如图所示的三角形区域,如果在这个区域内修建一个公园,要使公园到三个村庄的距离相等,那么这个公园应建的位置是△ABC的 ( )
A.三条高的交点
B.三边垂直平分线的交点
C.三条角平分线的交点
D.三条中线的交点
【参考答案】
交点
运用线段垂直平分线性质尺规作图
例2 如图,在△ABC中,以点A为圆心,AC的长为半径作圆弧交BC于点D,再分别以点B和点D为圆心,大于BD的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.若AB=9,AC=7,则△ADE的周长为 .
【参考答案】
例2 16
同课章节目录
