第二单元长方体(二)(知识梳理+拔高训练)二-2024-2025学年五年级数学下学期培优检测卷(北师大版)
文档属性
| 名称 | 第二单元长方体(二)(知识梳理+拔高训练)二-2024-2025学年五年级数学下学期培优检测卷(北师大版) |

|
|
| 格式 | docx | ||
| 文件大小 | 259.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 19:35:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二单元长方体(一)(知识梳理+拔高训练)二
知识梳理
知识点一:体积与容积
物体所占空间的大小,是物体的体积。容器所能容纳物体的体积,是容器的容积。
知识点二:体积单位
1.认识常见的体积单位
常见的体积单位有立方厘米、立方分米、立方米,分别记作厘米3(cm3)、分米3(dm3)、米3(m3)。
2.认识常见的容积单位
计量较大容器的容积时用升(L),计量较小容器的容积时用毫升(mL)。知识点三:长方体的体积
知识点三:长方体的体积
1.探究长、正方体体积的计算方法
长方体的体积= 长× 宽× 高,V = abh
正方体的体积= 棱长× 棱长× 棱长,V= a×a×a= a3
2.长、正方体体积计算的通用公式
长方体(正方体)的体积= 底面积× 高,用公式表示为:
V = Sh。
已知长方体的底面积、高、体积三个量中的任意两个量,可以求得第三个量。
知识点四:体积单位的换算
1.相邻两个体积单位之间的进率是1000。
2.1 m =1000 dm ,1 dm =1000 cm ,1 L=1000 mL
知识点五:有趣的测量
在测量不规则物体的体积时,水面升高部分水的体积(或水满杯时溢出的水的体积)等于不规则物体的体积。
拔高训练
一、填空题(共20分)
1.(2分)一个表面积为110平方厘米的长方体正好切成5个相同的小正方体,每个小正方体的表面积是( )平方厘米。
2.(2分)一个长方体木块的表面积为42cm2,正好可以截成三个完全一样的小正方体(如图),每个小正方体的表面积是( )cm2。
3.(2分)把一个长15分米,宽8分米,高6分米的长方体截成两个同样的长方体,则它的表面积最多增加( )平方分米,至少增加( )平方分米。
4.(2分)如图,一个大正方体的表面积是12dm2,把它分成两个完全相同的长方体,每个长方体的表面积是( )dm2。
5.(2分)一个长方体底面是边长为8cm的正方形,高为20cm,这个长方体的棱长总和是( )cm。
6.(2分)一个长方体的棱长总和是64厘米,它的底面是一个周长为24厘米的长方形,它的高是( )厘米。
7.(2分)下图是正方体的展开图,折叠后“学”字对面的字是( )。
8.(2分)如下图,把一些棱长是5cm的小正方体堆放在墙角,这堆小正方体露在外面的面积是( )cm2。
9.(2分)如图,三个正方体的棱长分别为1厘米、2厘米、4厘米,此组合体的表面积是( )平方厘米。
10.(2分)一个长5分米、宽3分米、高4分米的石膏长方体,最好选用面积为( )平方分米的面为底面放置最安全。
二、判断题(共10分)
11.(2分)一个物体从一个面看到正方形,这个物体一定是正方体。( )
12.(2分)因为长方体有6个面,8个顶点,12条棱,所以有6个面,8个顶点,12条棱的几何体一定是长方体。( )
13.(2分)从一个棱长为2厘米的正方体(如图1)的一个顶点处挖去一个棱长为1厘米的小正方体,得到图2,图1和图2的表面积相等。( )
14.(2分)3个相同的正方体放在墙角处,至少有9个面露在外面。( )
15.(2分)一个长方体的长、宽、高都扩大到原来的2倍。它的棱长之和就扩大到原来的8倍。( )
三、选择题(共10分)
16.(2分)下面四个图形中,不能折叠成正方体的是( )。
A. B. C. D.
17.(2分)用一根长60厘米的铁丝,可以焊成一个长6厘米,宽4厘米,高( )厘米的长方体框架。
A.2 B.3 C.4 D.5
18.(2分)将按下图的方式摆放在桌面上,则第⑥个图形有( )个面露在外面。
A.20 B.7 C.30 D.36
19.(2分)两个棱长5cm的正方体拼成一个长方体,表面积是( )cm2。
A.25 B.150 C.250 D.300
20.(2分)把一个棱长为5cm的正方体锯成两个小长方体,表面积比原来增加了( )cm2。
A.50 B.25 C.20 D.10
四、计算题(共6分)
21.(6分)求下列图形的表面积。(单位:)
五、作图题(共6分)
22.(6分)下面是不完整的正方体展开图,请把它补充完整。
六、解答题(共48分)
23.(6分)教室的长12米、宽8米、高3.5米,要粉刷教室的四面墙壁和顶棚(除去门窗和黑板的面积15.5平方米),共要粉刷多大的面积?
24.(6分)一个长方体礼盒长20厘米、宽15厘米,高12厘米,笑笑要把它的各面都贴上彩纸,至少需要多少平方厘米的彩纸?
25.(6分)游泳中心新建了一个长50米、宽25米、深2米的游泳池。现要在游泳池四周和底面都贴上瓷砖,如果每平方米需要32元,一共需要多少元?
26.(6分)一个长方体,如果高减少,就变成了一个棱长的正方体。那么长方体变成正方体后的表面积减少了多少?
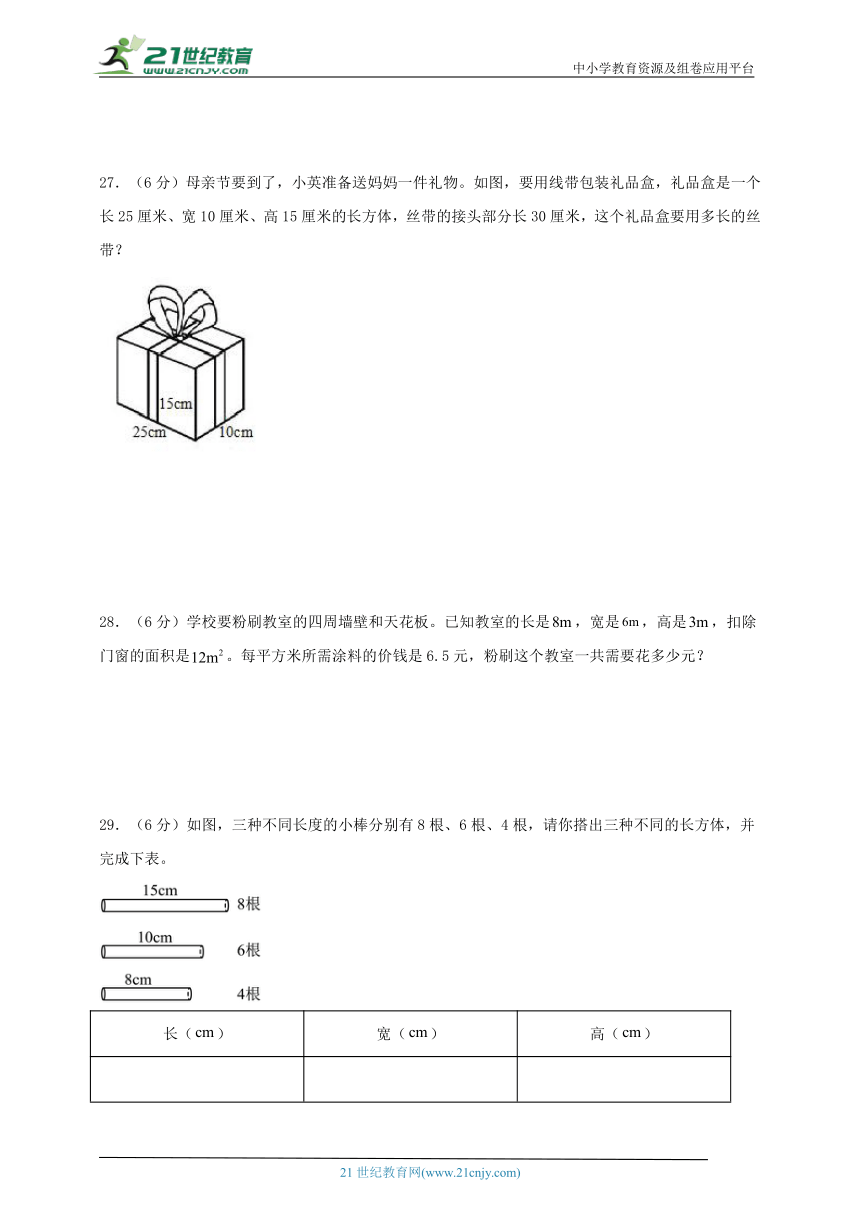
27.(6分)母亲节要到了,小英准备送妈妈一件礼物。如图,要用线带包装礼品盒,礼品盒是一个长25厘米、宽10厘米、高15厘米的长方体,丝带的接头部分长30厘米,这个礼品盒要用多长的丝带?
28.(6分)学校要粉刷教室的四周墙壁和天花板。已知教室的长是,宽是,高是,扣除门窗的面积是。每平方米所需涂料的价钱是6.5元,粉刷这个教室一共需要花多少元?
29.(6分)如图,三种不同长度的小棒分别有8根、6根、4根,请你搭出三种不同的长方体,并完成下表。
长() 宽() 高()
30.(6分)一个工艺品盒的长是8厘米,宽是6厘米,高是2厘米,现将4个这样的工艺品盒包装在一起,至少需要多少平方厘米的包装纸?(接口处忽略不计)
参考答案
1.30
【分析】根据题意,一个长方体可以切成5个小正方体,由此可知,这个长方体的底面是正方形,长方体的长是宽(高)的5倍,这个长方体的表面积相当于一个底面面积的22倍,由此可以求出长方体底面的面积,再根据正方体的表面积公式:S=6a2,把数据代入公式解答。
【详解】根据分析可知:
(平方厘米)
【点睛】此题主要考查长方体、正方体表面积公式的灵活运用,关键是熟记公式。
2.18
【分析】三个小正方体拼在一起组成原来的长方体,减少了4个面,所以这个长方体的表面积相当于小正方体的14个面的面积,由此可以求出小正方体的一个面的面积,进而求出每个小正方体的表面积;据此解答。
【详解】42÷14×6
=3×6
=18(cm2)
答:每个小正方体的表面积是18cm2。
【点睛】此题解题的关键应明确把一个长方体分成n个小正方体,切n-1次,增加2(n-1)个面。
3. 240 96
【分析】根据题意,把这个长方体切成两个同样的小长方体,要使表面积增加的最多,也就是与原来长方体的最大面平行切开;要使表面积增加的最少,也就是与原来长方体的最小面平行切开;表面积增加两个切面的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】增加最大:15×8×2
=120×2
=240(平方分米)
增加最小:8×6×2
=48×2
=96(平方分米)
【点睛】利用立体图形的切拼方法,以及长方形的面积公式解答问题;关键明确如果截成最大面与最小面。
4.8
【分析】把一个正方体平均分成两个完全相同的长方体,增加了2个面,则每个长方体的表面积是正方体4个面的面积,据此解答。
【详解】12÷6×4
=2×4
=8(dm2)
【点睛】此题考查了立体图形的切拼,把正方体分成两个长方体,表面积增加了两个面。
5.144
【分析】由题意可知长方体的长是8cm,宽是8cm,高是20cm,根据长方体的棱长和=(a+b+h)×4,列式解答即可。
【详解】(8+8+20)×4
=(16+20)×4
=36×4
=144(cm)
这个长方体的棱长总和是144cm。
【点睛】此题主要考查长方体棱长的应用,根据公式解答即可。
6.4
【分析】长方体特征为:6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面面积和周长都相等,12条棱分3组,每组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4。此题中一个长方体的棱长总和是64厘米,它的底面是一个周长为24厘米的长方形,则它的另外一个底面周长同样也是24厘米,用棱长和减去两个底面的周长之和,可得4条高的长度,除以4即为1条高的长度。
【详解】4条高的长度为:
64-24×2
=64-48
=16(厘米)
1条高的长度为:
16÷4=4(厘米)
【点睛】此题主要考查了对长方体特征的掌握程度,同时要求对棱长总和计算方法能够联系题目灵活运用。
7.知
【分析】正方体的展开图相邻的面不相对,相对的面不相邻,相对的面中间隔开一个;据此解答。
【详解】由正方体展开图的特征可知:“学”字对面的字是“知”;“爱”字对面的字是“习”;“长”字对面的字是“识”。
所以折叠后“学”字对面的字是“知”。
8.250
【分析】
从图意可知:露在外面的面有:从前面看,有3个小正方形;从右面看,有3个小正方形;从上面看,有4个小正方形。露在外面的面一共有3+3+4=10个小正方形,先求一个正方形的面积,再乘10即可求出露在外面的面积。据此解答。
【详解】5×5×(3+3+4)
=25×10
=250(cm2)
这堆小正方体露在外面的面积是250cm2。
9.116
【分析】观察图形可知,用原来三个正方体的表面积之和减去遮住的四个正方形面积即是此组合体的表面积。正方体的表面积=棱长×棱长×6,正方形的面积=边长×边长,据此分别代入数据进行计算。
【详解】4×4×6+2×2×6+1×1×6
=96+24+6
=126(平方厘米)
126-2×2×2-1×1×2
=126-8-2
=116(平方厘米)
【点睛】本题考查组合体的表面积。明确组合体表面积的意义及遮住的四个正方形面积的计算是解题的关键。
10.20
【分析】要想放置最安全,就要选择占地面积最大的面,根据长方体特征,进行解答。
【详解】以长为5分米,宽为3分米为面占地面积:5×3=15(平方分米)
以长为5分米,高为4分米为面占地面积:5×4=20(平方分米)
以宽为4分米,高为3分米为面占地面积:4×3=12(平方分米)
20>15>12
最好选用20平方分米的面为地面放置最安全。
【点睛】本题考查长方体六个面的面积大小的比较,根据长方体的特征,解答问题。
11.×
【分析】正方体的6个面都是正方形,从任何一个面看都是正方形。一般情况下长方体的6个面都是长方形。也有一对面是正方形,其它4个面是长方形的长方体,此时从一个面看可能看到正方形,据此解答。
【详解】由分析可知,当一个长方体中有一对面是正方形时,从一个面看到的可能是正方形,原题说法错误。
故答案为:×
【点睛】此题考查了长方体和正方体的特征,明确长方体的特殊情况,当有4个面相同时,另外2个面是正方形。
12.×
【分析】长方体有6个面,8个顶点,12条棱,长方体的每组相对的面完全相等,相对的四条棱长相等;但是有6个面,8个顶点,12条棱不一定是长方形,如下图,棱台有6个面,8个顶点,12条棱,但它不是长方体,据此解答。
【详解】由分析可知,棱台也有12条棱、6个面、8个顶点,但不一定是长方体。
原题干说法是错误的。
故答案为:×
【点睛】根据长方体的特征进行解答。
13.√
【分析】观察图形可知,从顶点处挖去一个小正方体,小正方体外露的三个面正好可以补上原正方体缺失部分,所以表面积不变;据此判断即可。
【详解】根据分析可知,挖去小正方体后,剩下的图形的表面积与原正方体的面表积相等;原题说法正确。
故答案为:√
【点睛】本题考查了几何体表面积的计算,明确挖去的正方体中相对的面的面积都相等是此题关键。
14.×
【分析】将3个相同的正方体放在墙角处,如图有三种不同的方法:
,数出露在外面的面一共有几个,再进一步解答即可。
【详解】由分析可知:可以摆如下图所示的三种情况。
以上三种直观图露在外面的面都是7个,原说法错误。
故答案为:×
【点睛】此题考查立体图形的拼组,解答此题的关键是弄清楚每个图形露在外面的面的个数。
15.×
【分析】假设长方体的长、宽、高分别为a、b、c,则扩大后长、宽、高分别为2a、2b、2c;再根据棱长总和公式:棱长总和=(长+宽+高)×4,分别求出扩大前和扩大后棱长总和,再用扩大后棱长总和除以扩大前棱长总和,即可解答。
【详解】假设长方体的长、宽、高分别为a、b、c,扩大后长、宽、高分别为2a、2b、2c;
长方体棱长扩大前棱长总和:(a+b+c)×4
长方体棱长扩大后棱长总和:(2a+2b+2c)×4
=2×(a+b+c)×4
=(a+b+c)×8
(a+b+c)×8÷(a+b+c)×4=2
一个长方体的长、宽、高都扩大到原来的2倍。它的棱长之和就扩大到原来的2倍。
原题干说法错误。
故答案为:×
【点睛】熟练掌握长方体的棱长总和计算公式并能灵活利用是解答本题的关键。
16.B
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:
(1)一条线上不过四;
(2)“田字形”“七字型”“凹字型”;据此解答。
【详解】由分析可知:
A.属于“2—3—1”型,能折叠成正方体;
B.不属于正方体的展开图类型,不能折叠成正方体,折叠时有重叠的面;
C.属于“2—3—1”型,能折叠成正方体;
D.属于“1—4—1”型,能折叠成正方体。
故答案为:B
【点睛】本题考查正方体展开图。有11种情况,分四种类型: “1-4-1”结构、“2-2-2”结构、“3-3”结构和“2-3-1”结构。
17.D
【分析】用一根60厘米长的铁丝,恰好可以焊成长方体,这个长方体的棱长总和就是60厘米,长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4减去长和宽,即可求出高,据此解答。
【详解】60÷4-(6+4)
=15-10
=5(厘米)
用一根长60厘米的铁丝,可以焊成一个长6厘米,宽4厘米,高5厘米的长方体框架。
故答案为:D
【点睛】此题主要考查长方体的棱长总和公式的灵活运用,结合题意分析解答即可。
18.A
【分析】1个小正方体有5个面露在外面,再增加一个正方体,2个小正方体有8个面露在外面;3个小正方体有11个面露在外面;每增加1个小正方体就增加3个面。由此相加即可求解。
【详解】5+3+3+3+3+3
=8+3+3+3+3
=11+3+3+3
=14+3+3
=17+3
=20(个)
将按下图的方式摆放在桌面上,则第⑥个图形有20个面露在外面。
故答案为:A
【点睛】解答此题应根据题意,进行推导,得出规律:即1个小正方体露出5个面,每增加1个小正方体增加3个面;进行解答即可。
19.C
【分析】两个正方体拼成一个长方体后,表面积比原来是减少了两个正方体的面的面积,由此即可解答。
【详解】5×5×(6×2-2)
=25×10
=250(cm2)
这个长方体的表面积是250cm2。
故答案为:C
【点睛】抓住两个正方体拼组长方体的方法,得出表面积是减少了2个正方体的面的面积。
20.A
【分析】根据题意可知:把1个棱长5厘米的正方体木块截成两个完全一样的长方体,表面积增加了两个截面的面积,根据正方形的面积公式:s=a2,把数据代入公式解答。
【详解】5×5×2
=25×2
=50(cm2)
表面积增加了50 cm2。
故答案为:A
【点睛】此题主要考查正方形面积公式的灵活运用,关键是明确:把1个棱长5厘米的正方体木块截成两个完全一样的长方体,表面积增加了两个截面的面积。
21.304cm2;384cm2
【分析】(1)根据,代入数据计算即可。
(2)根据正方体的表面积=棱长×棱长×6,代入数据计算即可。
【详解】(1)
(cm2)
(2)
(cm2)
22.见详解
【分析】根据正方体展开图,可把此图补充成正方体展开图的“1-3-2”型,即在中行左边添加一个相同的正方形或在中列的上面添加一个相同的正方形。
【详解】
【点睛】本题主要是考查正方体展开图的特征,正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
23.220.5平方米
【分析】因为地面不要粉刷,在教室的四面墙壁和顶棚粉刷,用长方体表面积公式:S=2ab+2ah+2bh减去一个下底面积,代入数据求解最后减去门窗和黑板的面积即可;
【详解】由分析可得:
12×8+12×3.5×2+8×3.5×2-15.5
=96+42×2+28×2-15.5
=96+84+56-15.5
=180+56-15.5
=236-15.5
=220.5(平方米)
答:共要粉刷220.5平方米的面积。
【点睛】本题主要考查了长方体表面积公式的应用,需要熟练掌握公式的同时还要会和题目中的实际情况相结合。
24.1440平方厘米
【分析】根据题意,求贴彩纸的面积,就是求这个长方体的表面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(20×15+20×12+15×12)×2
=(300+240+180)×2
=(540+180)×2
=720×2
=1440(平方厘米)
答:至少需要1440平方厘米的彩纸。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
25.49600元
【分析】根据题意,先求贴瓷砖的面积,即长方体游泳池5个面积的面积和;根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,求出贴瓷砖的面积,再乘32,即可求出需要的钱数。
【详解】[50×25+(50×2+25×2)×2]×32
=[1250+(100+50)×2]×32
=[1250+150×2]×32
=[1250+300]×32
=1550×32
=49600(元)
答:一共需要49600元。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
26.240平方厘米
【分析】根据题意,一个长方体如果高减少6cm,就变成一个棱长10cm的正方体,长方体的长=长方体的宽=正方体棱长=10cm;求减少部分的面积,就是一个长是10cm,宽是10cm,高是6cm的长方体的侧面积;且这四个面相等;根据长方形面积公式:长×高,代入数据,即可解答。
【详解】10×6×4
=60×4
=240(cm2)
答:长方体变成正方体后的表面积减少了240平方厘米。
【点睛】解答本题的关键是明确减少后的长方体的长与宽和正方体棱长的关系。
27.160厘米
【分析】由图可知:包装礼品盒所需线带的长度等于长方体的2条长加上2条宽加上4条高,再加上接头部分长度。
【详解】
=160(厘米)
答:这个礼品盒要用160厘米的丝带。
【点睛】此题主要考查的目的是理解掌握长方体的特征,关键是弄清需要求哪几条棱的长度。
28.780元
【分析】根据题意可知,求长方体5个面的面积,再减去门窗的面积,根据长方体表面积公式:长×宽+(长×高+宽×高)×2,求出表面积,最后再乘6.5元,就是粉刷这个教室一共需要的钱数。
【详解】8×6+(8×3+6×3)×2-12
=48+(24+18)×2-12
=48+42×2-12
=48+84-12
=132-12
=120(平方米)
120×6.5=780(元)
答:粉刷这个教室一共需要花780元。
【点睛】本题考查长方形表面积公式的应用,注意是5个面的面积。
29.见详解
【分析】(1)根据长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,可以用15cm、10cm、8cm长的小棒各4根,搭出一个长、宽、高分别是15cm、10cm、8cm的长方体;
(2)根据长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,可以用15cm长的小棒8根,10cm长的小棒4根,搭出一个长、宽、高分别是15cm、15cm、10cm的长方体;
(3)根据长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,可以用15cm长的小棒8根,8cm长的小棒4根,搭出一个长、宽、高分别是15cm、15cm、8cm的长方体。
【详解】根据分析可得:
长() 宽() 高()
15 10 8
15 15 10
15 15 8
【点睛】此题主要考查了长方体的特征和应用,要熟练掌握,进行解答。
30.320平方厘米
【分析】要想使包装纸最省,只要把工艺品盒的最大面相对,使它们相对在一起后的表面积减少的最多即可;工艺品盒的最大面是8×6的面,把4个工艺品盒的8×6的面依次拼组在一起,此时这个拼组成的长方体的长是8cm,宽是6cm,高是2×4=8cm,利用长方体的表面积公式S=(ab+ah+bh)×2,代入数值计算即可。
【详解】(8×6+8×8+6×8)×2
=160×2
=320(平方厘米)
答:至少需要320平方厘米的包装纸。
【点睛】此题主要根据长方体的拼组方法和长方体的表面积的计算方法解决问题,关键是根据拼组方法得出表面积最小的拼组方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元长方体(一)(知识梳理+拔高训练)二
知识梳理
知识点一:体积与容积
物体所占空间的大小,是物体的体积。容器所能容纳物体的体积,是容器的容积。
知识点二:体积单位
1.认识常见的体积单位
常见的体积单位有立方厘米、立方分米、立方米,分别记作厘米3(cm3)、分米3(dm3)、米3(m3)。
2.认识常见的容积单位
计量较大容器的容积时用升(L),计量较小容器的容积时用毫升(mL)。知识点三:长方体的体积
知识点三:长方体的体积
1.探究长、正方体体积的计算方法
长方体的体积= 长× 宽× 高,V = abh
正方体的体积= 棱长× 棱长× 棱长,V= a×a×a= a3
2.长、正方体体积计算的通用公式
长方体(正方体)的体积= 底面积× 高,用公式表示为:
V = Sh。
已知长方体的底面积、高、体积三个量中的任意两个量,可以求得第三个量。
知识点四:体积单位的换算
1.相邻两个体积单位之间的进率是1000。
2.1 m =1000 dm ,1 dm =1000 cm ,1 L=1000 mL
知识点五:有趣的测量
在测量不规则物体的体积时,水面升高部分水的体积(或水满杯时溢出的水的体积)等于不规则物体的体积。
拔高训练
一、填空题(共20分)
1.(2分)一个表面积为110平方厘米的长方体正好切成5个相同的小正方体,每个小正方体的表面积是( )平方厘米。
2.(2分)一个长方体木块的表面积为42cm2,正好可以截成三个完全一样的小正方体(如图),每个小正方体的表面积是( )cm2。
3.(2分)把一个长15分米,宽8分米,高6分米的长方体截成两个同样的长方体,则它的表面积最多增加( )平方分米,至少增加( )平方分米。
4.(2分)如图,一个大正方体的表面积是12dm2,把它分成两个完全相同的长方体,每个长方体的表面积是( )dm2。
5.(2分)一个长方体底面是边长为8cm的正方形,高为20cm,这个长方体的棱长总和是( )cm。
6.(2分)一个长方体的棱长总和是64厘米,它的底面是一个周长为24厘米的长方形,它的高是( )厘米。
7.(2分)下图是正方体的展开图,折叠后“学”字对面的字是( )。
8.(2分)如下图,把一些棱长是5cm的小正方体堆放在墙角,这堆小正方体露在外面的面积是( )cm2。
9.(2分)如图,三个正方体的棱长分别为1厘米、2厘米、4厘米,此组合体的表面积是( )平方厘米。
10.(2分)一个长5分米、宽3分米、高4分米的石膏长方体,最好选用面积为( )平方分米的面为底面放置最安全。
二、判断题(共10分)
11.(2分)一个物体从一个面看到正方形,这个物体一定是正方体。( )
12.(2分)因为长方体有6个面,8个顶点,12条棱,所以有6个面,8个顶点,12条棱的几何体一定是长方体。( )
13.(2分)从一个棱长为2厘米的正方体(如图1)的一个顶点处挖去一个棱长为1厘米的小正方体,得到图2,图1和图2的表面积相等。( )
14.(2分)3个相同的正方体放在墙角处,至少有9个面露在外面。( )
15.(2分)一个长方体的长、宽、高都扩大到原来的2倍。它的棱长之和就扩大到原来的8倍。( )
三、选择题(共10分)
16.(2分)下面四个图形中,不能折叠成正方体的是( )。
A. B. C. D.
17.(2分)用一根长60厘米的铁丝,可以焊成一个长6厘米,宽4厘米,高( )厘米的长方体框架。
A.2 B.3 C.4 D.5
18.(2分)将按下图的方式摆放在桌面上,则第⑥个图形有( )个面露在外面。
A.20 B.7 C.30 D.36
19.(2分)两个棱长5cm的正方体拼成一个长方体,表面积是( )cm2。
A.25 B.150 C.250 D.300
20.(2分)把一个棱长为5cm的正方体锯成两个小长方体,表面积比原来增加了( )cm2。
A.50 B.25 C.20 D.10
四、计算题(共6分)
21.(6分)求下列图形的表面积。(单位:)
五、作图题(共6分)
22.(6分)下面是不完整的正方体展开图,请把它补充完整。
六、解答题(共48分)
23.(6分)教室的长12米、宽8米、高3.5米,要粉刷教室的四面墙壁和顶棚(除去门窗和黑板的面积15.5平方米),共要粉刷多大的面积?
24.(6分)一个长方体礼盒长20厘米、宽15厘米,高12厘米,笑笑要把它的各面都贴上彩纸,至少需要多少平方厘米的彩纸?
25.(6分)游泳中心新建了一个长50米、宽25米、深2米的游泳池。现要在游泳池四周和底面都贴上瓷砖,如果每平方米需要32元,一共需要多少元?
26.(6分)一个长方体,如果高减少,就变成了一个棱长的正方体。那么长方体变成正方体后的表面积减少了多少?
27.(6分)母亲节要到了,小英准备送妈妈一件礼物。如图,要用线带包装礼品盒,礼品盒是一个长25厘米、宽10厘米、高15厘米的长方体,丝带的接头部分长30厘米,这个礼品盒要用多长的丝带?
28.(6分)学校要粉刷教室的四周墙壁和天花板。已知教室的长是,宽是,高是,扣除门窗的面积是。每平方米所需涂料的价钱是6.5元,粉刷这个教室一共需要花多少元?
29.(6分)如图,三种不同长度的小棒分别有8根、6根、4根,请你搭出三种不同的长方体,并完成下表。
长() 宽() 高()
30.(6分)一个工艺品盒的长是8厘米,宽是6厘米,高是2厘米,现将4个这样的工艺品盒包装在一起,至少需要多少平方厘米的包装纸?(接口处忽略不计)
参考答案
1.30
【分析】根据题意,一个长方体可以切成5个小正方体,由此可知,这个长方体的底面是正方形,长方体的长是宽(高)的5倍,这个长方体的表面积相当于一个底面面积的22倍,由此可以求出长方体底面的面积,再根据正方体的表面积公式:S=6a2,把数据代入公式解答。
【详解】根据分析可知:
(平方厘米)
【点睛】此题主要考查长方体、正方体表面积公式的灵活运用,关键是熟记公式。
2.18
【分析】三个小正方体拼在一起组成原来的长方体,减少了4个面,所以这个长方体的表面积相当于小正方体的14个面的面积,由此可以求出小正方体的一个面的面积,进而求出每个小正方体的表面积;据此解答。
【详解】42÷14×6
=3×6
=18(cm2)
答:每个小正方体的表面积是18cm2。
【点睛】此题解题的关键应明确把一个长方体分成n个小正方体,切n-1次,增加2(n-1)个面。
3. 240 96
【分析】根据题意,把这个长方体切成两个同样的小长方体,要使表面积增加的最多,也就是与原来长方体的最大面平行切开;要使表面积增加的最少,也就是与原来长方体的最小面平行切开;表面积增加两个切面的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】增加最大:15×8×2
=120×2
=240(平方分米)
增加最小:8×6×2
=48×2
=96(平方分米)
【点睛】利用立体图形的切拼方法,以及长方形的面积公式解答问题;关键明确如果截成最大面与最小面。
4.8
【分析】把一个正方体平均分成两个完全相同的长方体,增加了2个面,则每个长方体的表面积是正方体4个面的面积,据此解答。
【详解】12÷6×4
=2×4
=8(dm2)
【点睛】此题考查了立体图形的切拼,把正方体分成两个长方体,表面积增加了两个面。
5.144
【分析】由题意可知长方体的长是8cm,宽是8cm,高是20cm,根据长方体的棱长和=(a+b+h)×4,列式解答即可。
【详解】(8+8+20)×4
=(16+20)×4
=36×4
=144(cm)
这个长方体的棱长总和是144cm。
【点睛】此题主要考查长方体棱长的应用,根据公式解答即可。
6.4
【分析】长方体特征为:6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面面积和周长都相等,12条棱分3组,每组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4。此题中一个长方体的棱长总和是64厘米,它的底面是一个周长为24厘米的长方形,则它的另外一个底面周长同样也是24厘米,用棱长和减去两个底面的周长之和,可得4条高的长度,除以4即为1条高的长度。
【详解】4条高的长度为:
64-24×2
=64-48
=16(厘米)
1条高的长度为:
16÷4=4(厘米)
【点睛】此题主要考查了对长方体特征的掌握程度,同时要求对棱长总和计算方法能够联系题目灵活运用。
7.知
【分析】正方体的展开图相邻的面不相对,相对的面不相邻,相对的面中间隔开一个;据此解答。
【详解】由正方体展开图的特征可知:“学”字对面的字是“知”;“爱”字对面的字是“习”;“长”字对面的字是“识”。
所以折叠后“学”字对面的字是“知”。
8.250
【分析】
从图意可知:露在外面的面有:从前面看,有3个小正方形;从右面看,有3个小正方形;从上面看,有4个小正方形。露在外面的面一共有3+3+4=10个小正方形,先求一个正方形的面积,再乘10即可求出露在外面的面积。据此解答。
【详解】5×5×(3+3+4)
=25×10
=250(cm2)
这堆小正方体露在外面的面积是250cm2。
9.116
【分析】观察图形可知,用原来三个正方体的表面积之和减去遮住的四个正方形面积即是此组合体的表面积。正方体的表面积=棱长×棱长×6,正方形的面积=边长×边长,据此分别代入数据进行计算。
【详解】4×4×6+2×2×6+1×1×6
=96+24+6
=126(平方厘米)
126-2×2×2-1×1×2
=126-8-2
=116(平方厘米)
【点睛】本题考查组合体的表面积。明确组合体表面积的意义及遮住的四个正方形面积的计算是解题的关键。
10.20
【分析】要想放置最安全,就要选择占地面积最大的面,根据长方体特征,进行解答。
【详解】以长为5分米,宽为3分米为面占地面积:5×3=15(平方分米)
以长为5分米,高为4分米为面占地面积:5×4=20(平方分米)
以宽为4分米,高为3分米为面占地面积:4×3=12(平方分米)
20>15>12
最好选用20平方分米的面为地面放置最安全。
【点睛】本题考查长方体六个面的面积大小的比较,根据长方体的特征,解答问题。
11.×
【分析】正方体的6个面都是正方形,从任何一个面看都是正方形。一般情况下长方体的6个面都是长方形。也有一对面是正方形,其它4个面是长方形的长方体,此时从一个面看可能看到正方形,据此解答。
【详解】由分析可知,当一个长方体中有一对面是正方形时,从一个面看到的可能是正方形,原题说法错误。
故答案为:×
【点睛】此题考查了长方体和正方体的特征,明确长方体的特殊情况,当有4个面相同时,另外2个面是正方形。
12.×
【分析】长方体有6个面,8个顶点,12条棱,长方体的每组相对的面完全相等,相对的四条棱长相等;但是有6个面,8个顶点,12条棱不一定是长方形,如下图,棱台有6个面,8个顶点,12条棱,但它不是长方体,据此解答。
【详解】由分析可知,棱台也有12条棱、6个面、8个顶点,但不一定是长方体。
原题干说法是错误的。
故答案为:×
【点睛】根据长方体的特征进行解答。
13.√
【分析】观察图形可知,从顶点处挖去一个小正方体,小正方体外露的三个面正好可以补上原正方体缺失部分,所以表面积不变;据此判断即可。
【详解】根据分析可知,挖去小正方体后,剩下的图形的表面积与原正方体的面表积相等;原题说法正确。
故答案为:√
【点睛】本题考查了几何体表面积的计算,明确挖去的正方体中相对的面的面积都相等是此题关键。
14.×
【分析】将3个相同的正方体放在墙角处,如图有三种不同的方法:
,数出露在外面的面一共有几个,再进一步解答即可。
【详解】由分析可知:可以摆如下图所示的三种情况。
以上三种直观图露在外面的面都是7个,原说法错误。
故答案为:×
【点睛】此题考查立体图形的拼组,解答此题的关键是弄清楚每个图形露在外面的面的个数。
15.×
【分析】假设长方体的长、宽、高分别为a、b、c,则扩大后长、宽、高分别为2a、2b、2c;再根据棱长总和公式:棱长总和=(长+宽+高)×4,分别求出扩大前和扩大后棱长总和,再用扩大后棱长总和除以扩大前棱长总和,即可解答。
【详解】假设长方体的长、宽、高分别为a、b、c,扩大后长、宽、高分别为2a、2b、2c;
长方体棱长扩大前棱长总和:(a+b+c)×4
长方体棱长扩大后棱长总和:(2a+2b+2c)×4
=2×(a+b+c)×4
=(a+b+c)×8
(a+b+c)×8÷(a+b+c)×4=2
一个长方体的长、宽、高都扩大到原来的2倍。它的棱长之和就扩大到原来的2倍。
原题干说法错误。
故答案为:×
【点睛】熟练掌握长方体的棱长总和计算公式并能灵活利用是解答本题的关键。
16.B
【分析】正方体的展开图类型:(1)“1—4—1”型:中间4个一连串,两边各一随便放;
(2)“2—3—1”型:二三紧连错一个,三一相连一随便;
(3)“2—2—2”型:两两相连各错一;
(4)“3—3”型:三个两排一对齐;
不能围成正方体的展开图类型:
(1)一条线上不过四;
(2)“田字形”“七字型”“凹字型”;据此解答。
【详解】由分析可知:
A.属于“2—3—1”型,能折叠成正方体;
B.不属于正方体的展开图类型,不能折叠成正方体,折叠时有重叠的面;
C.属于“2—3—1”型,能折叠成正方体;
D.属于“1—4—1”型,能折叠成正方体。
故答案为:B
【点睛】本题考查正方体展开图。有11种情况,分四种类型: “1-4-1”结构、“2-2-2”结构、“3-3”结构和“2-3-1”结构。
17.D
【分析】用一根60厘米长的铁丝,恰好可以焊成长方体,这个长方体的棱长总和就是60厘米,长方体的棱长总和=(长+宽+高)×4,用棱长总和除以4减去长和宽,即可求出高,据此解答。
【详解】60÷4-(6+4)
=15-10
=5(厘米)
用一根长60厘米的铁丝,可以焊成一个长6厘米,宽4厘米,高5厘米的长方体框架。
故答案为:D
【点睛】此题主要考查长方体的棱长总和公式的灵活运用,结合题意分析解答即可。
18.A
【分析】1个小正方体有5个面露在外面,再增加一个正方体,2个小正方体有8个面露在外面;3个小正方体有11个面露在外面;每增加1个小正方体就增加3个面。由此相加即可求解。
【详解】5+3+3+3+3+3
=8+3+3+3+3
=11+3+3+3
=14+3+3
=17+3
=20(个)
将按下图的方式摆放在桌面上,则第⑥个图形有20个面露在外面。
故答案为:A
【点睛】解答此题应根据题意,进行推导,得出规律:即1个小正方体露出5个面,每增加1个小正方体增加3个面;进行解答即可。
19.C
【分析】两个正方体拼成一个长方体后,表面积比原来是减少了两个正方体的面的面积,由此即可解答。
【详解】5×5×(6×2-2)
=25×10
=250(cm2)
这个长方体的表面积是250cm2。
故答案为:C
【点睛】抓住两个正方体拼组长方体的方法,得出表面积是减少了2个正方体的面的面积。
20.A
【分析】根据题意可知:把1个棱长5厘米的正方体木块截成两个完全一样的长方体,表面积增加了两个截面的面积,根据正方形的面积公式:s=a2,把数据代入公式解答。
【详解】5×5×2
=25×2
=50(cm2)
表面积增加了50 cm2。
故答案为:A
【点睛】此题主要考查正方形面积公式的灵活运用,关键是明确:把1个棱长5厘米的正方体木块截成两个完全一样的长方体,表面积增加了两个截面的面积。
21.304cm2;384cm2
【分析】(1)根据,代入数据计算即可。
(2)根据正方体的表面积=棱长×棱长×6,代入数据计算即可。
【详解】(1)
(cm2)
(2)
(cm2)
22.见详解
【分析】根据正方体展开图,可把此图补充成正方体展开图的“1-3-2”型,即在中行左边添加一个相同的正方形或在中列的上面添加一个相同的正方形。
【详解】
【点睛】本题主要是考查正方体展开图的特征,正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
23.220.5平方米
【分析】因为地面不要粉刷,在教室的四面墙壁和顶棚粉刷,用长方体表面积公式:S=2ab+2ah+2bh减去一个下底面积,代入数据求解最后减去门窗和黑板的面积即可;
【详解】由分析可得:
12×8+12×3.5×2+8×3.5×2-15.5
=96+42×2+28×2-15.5
=96+84+56-15.5
=180+56-15.5
=236-15.5
=220.5(平方米)
答:共要粉刷220.5平方米的面积。
【点睛】本题主要考查了长方体表面积公式的应用,需要熟练掌握公式的同时还要会和题目中的实际情况相结合。
24.1440平方厘米
【分析】根据题意,求贴彩纸的面积,就是求这个长方体的表面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(20×15+20×12+15×12)×2
=(300+240+180)×2
=(540+180)×2
=720×2
=1440(平方厘米)
答:至少需要1440平方厘米的彩纸。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
25.49600元
【分析】根据题意,先求贴瓷砖的面积,即长方体游泳池5个面积的面积和;根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,求出贴瓷砖的面积,再乘32,即可求出需要的钱数。
【详解】[50×25+(50×2+25×2)×2]×32
=[1250+(100+50)×2]×32
=[1250+150×2]×32
=[1250+300]×32
=1550×32
=49600(元)
答:一共需要49600元。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
26.240平方厘米
【分析】根据题意,一个长方体如果高减少6cm,就变成一个棱长10cm的正方体,长方体的长=长方体的宽=正方体棱长=10cm;求减少部分的面积,就是一个长是10cm,宽是10cm,高是6cm的长方体的侧面积;且这四个面相等;根据长方形面积公式:长×高,代入数据,即可解答。
【详解】10×6×4
=60×4
=240(cm2)
答:长方体变成正方体后的表面积减少了240平方厘米。
【点睛】解答本题的关键是明确减少后的长方体的长与宽和正方体棱长的关系。
27.160厘米
【分析】由图可知:包装礼品盒所需线带的长度等于长方体的2条长加上2条宽加上4条高,再加上接头部分长度。
【详解】
=160(厘米)
答:这个礼品盒要用160厘米的丝带。
【点睛】此题主要考查的目的是理解掌握长方体的特征,关键是弄清需要求哪几条棱的长度。
28.780元
【分析】根据题意可知,求长方体5个面的面积,再减去门窗的面积,根据长方体表面积公式:长×宽+(长×高+宽×高)×2,求出表面积,最后再乘6.5元,就是粉刷这个教室一共需要的钱数。
【详解】8×6+(8×3+6×3)×2-12
=48+(24+18)×2-12
=48+42×2-12
=48+84-12
=132-12
=120(平方米)
120×6.5=780(元)
答:粉刷这个教室一共需要花780元。
【点睛】本题考查长方形表面积公式的应用,注意是5个面的面积。
29.见详解
【分析】(1)根据长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,可以用15cm、10cm、8cm长的小棒各4根,搭出一个长、宽、高分别是15cm、10cm、8cm的长方体;
(2)根据长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,可以用15cm长的小棒8根,10cm长的小棒4根,搭出一个长、宽、高分别是15cm、15cm、10cm的长方体;
(3)根据长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱,可以用15cm长的小棒8根,8cm长的小棒4根,搭出一个长、宽、高分别是15cm、15cm、8cm的长方体。
【详解】根据分析可得:
长() 宽() 高()
15 10 8
15 15 10
15 15 8
【点睛】此题主要考查了长方体的特征和应用,要熟练掌握,进行解答。
30.320平方厘米
【分析】要想使包装纸最省,只要把工艺品盒的最大面相对,使它们相对在一起后的表面积减少的最多即可;工艺品盒的最大面是8×6的面,把4个工艺品盒的8×6的面依次拼组在一起,此时这个拼组成的长方体的长是8cm,宽是6cm,高是2×4=8cm,利用长方体的表面积公式S=(ab+ah+bh)×2,代入数值计算即可。
【详解】(8×6+8×8+6×8)×2
=160×2
=320(平方厘米)
答:至少需要320平方厘米的包装纸。
【点睛】此题主要根据长方体的拼组方法和长方体的表面积的计算方法解决问题,关键是根据拼组方法得出表面积最小的拼组方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
