第二单元认识三角形和四边形(知识梳理+拔高训练)一-2024-2025学年四年级数学下学期培优检测卷(北师大版)
文档属性
| 名称 | 第二单元认识三角形和四边形(知识梳理+拔高训练)一-2024-2025学年四年级数学下学期培优检测卷(北师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 496.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 19:38:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二单元认识三角形和四边形(知识梳理+拔高训练)一
知识梳理
知识点一:图形分类
四边形容易变形,三角形具有稳定性。四边形和三角形的这些特性在生产和生活中有着广泛应用。
知识点二:三角形分类
判断一个三角形是锐角三角形、直角三角形还是钝角三角形,关键是看它最大的角,最大的角是哪类角,它就属于哪类三角形。
知识点三:三角形内角和
三角形的内角和不会随着三角形的大小、形状变化而发生变化,所有三角形的内角和都是180°。
知识点四:三角形边的关系
三角形任意两边之和大于第三边,任意两边之差小于第三边。
知识点五:四边形分类
四边形按照边的特点,可以把四边形分为:平行四边形、梯形和任意四边形三大类。正方形和长方形都是特殊的平行四边形。
拔高训练
一、填空题(共20分)
1.(2分)有一块等腰三角形的菜地,它的周长是236米,腰长83米,这块等腰三角形菜地的底边长是( )米。
2.(2分)爷爷给一块地围上篱笆,这样围十分牢固。依据的原理是三角形具有( )。
3.(2分)把平行四边形的各个角撕下来拼在一起,拼成的角是( )角,是( )°。
4.(2分)一个等腰梯形的周长为23厘米,上底和下底分别为5厘米和8厘米,这个等腰梯形的腰长是( )厘米;如果将这个梯形的上底增加3厘米,下底不变,会变成一个( )。
5.(2分)淘气准备用小棒以首尾相接的方式围一个三角形,已经有7厘米和5厘米两根小棒,他还需要一根小棒(取整厘米数),这根小棒最长可以是( )厘米,最短可以是( )厘米。
6.(2分)如果一个三角形两条边分别长6厘米和11厘米。如果第三条边的长度也为整数厘米数,第三条边的长度有( )种可能。
7.(2分)一个三角形中,有一个角是75°,一个角是63°,按角的大小分,这个三角形是( )三角形。
8.(2分)红领巾是少先队员的标志,代表红旗的一角。一种红领巾的底角是,它的顶角是( ),这是一个( )三角形。
9.(2分)第一组小棒:4cm、4cm、4cm;第二组小棒:3cm、4cm、5cm;第三组小棒:5cm、6cm、7cm;第四组小棒:4cm、4cm、5cm。用上述四组小棒分别围一个三角形,可以围成一个直角三角形的是第( )组小棒。(用上圆规画一画、试一试)。
10.(2分)三角形具有( )性。1个平角等于( )个直角。
二、判断题(共10分)
11.(2分)平行四边形的两组对边互相平行。( )
12.(2分)在一个等腰三角形中,有两条边的长度分别是4厘米和9厘米,这个三角形的周长可能是17厘米,也可能是22厘米。( )
13.(2分)三角形和正方形都具有稳定性。( )
14.(2分)长8.6厘米、8.6厘米、16厘米的三条线段可以围成一个等腰三角形。( )
15.(2分)一个三角形中,其中两个角的度数分别是15°和85°,按角分,这是一个钝角三角形。( )
三、选择题(共10分)
16.(2分)小敏不小心将一块玻璃打碎成了如图的4块。为了能在商店配到一块与原来相同的平行四边形玻璃,他只带了两块碎玻璃,其编号应该是( )。
A.①和② B.②和③ C.③和④ D.②和④
17.(2分)如图藏在云朵后面的图形不可能是( )。
A.锐角三角形 B.钝角三角形 C.梯形 D.平行四边形
18.(2分)一个三角形中,其中两个角的和是80°,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
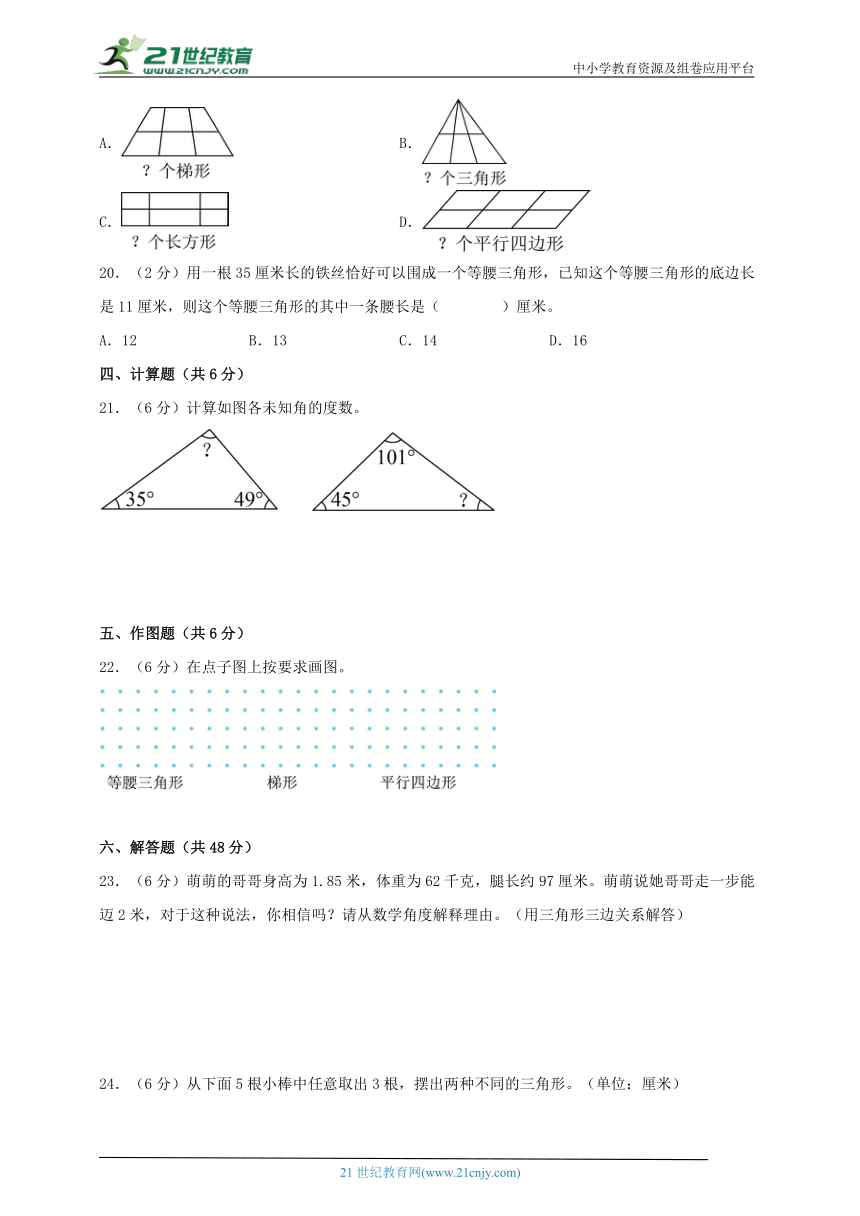
19.(2分)下面四幅图中,按要求数图形的结果跟其他三幅不一样的是( )。
A. B.
C. D.
20.(2分)用一根35厘米长的铁丝恰好可以围成一个等腰三角形,已知这个等腰三角形的底边长是11厘米,则这个等腰三角形的其中一条腰长是( )厘米。
A.12 B.13 C.14 D.16
四、计算题(共6分)
21.(6分)计算如图各未知角的度数。
五、作图题(共6分)
22.(6分)在点子图上按要求画图。
六、解答题(共48分)
23.(6分)萌萌的哥哥身高为1.85米,体重为62千克,腿长约97厘米。萌萌说她哥哥走一步能迈2米,对于这种说法,你相信吗?请从数学角度解释理由。(用三角形三边关系解答)
24.(6分)从下面5根小棒中任意取出3根,摆出两种不同的三角形。(单位:厘米)
25.(6分)奇奇在数学课上画了一个等腰三角形,已知他画的等腰三角形中的一个角是。你知道他画的等腰三角形中另外两个角分别是多少度吗?
26.(6分)王大爷靠墙种一块菜地(如图),如果他想用篱笆把这块菜地围起来,至少要用篱笆多少米?
27.(6分)小明用一根铁丝刚好围成一个边长是15厘米的正方形,如果用这根铁丝围成一个等边三角形,三角形的边长是多少厘米?
28.(6分)一根铁丝正好围成一个边长为8分米的等边三角形。如果用这根铁丝围成一个底边为6分米的等腰三角形,那么这个等腰三角形的一条腰长是多少分米?
29.(6分)“数学来源于生活又运用于生活”,你能用所学的数学知识解释下面的生活现象吗?
30.(6分)拼一拼。
下面哪两个图形能拼成长方形、平行四边形、梯形?剪下附页3图3中的图形试一试。
参考答案
1.70
【分析】等腰三角形两条腰相等,底边=三角形周长-腰长×2,即可解答。
【详解】236-83×2
=236-166
=70(米)
故这块等腰三角形菜地的底边长是70米。
2.稳定性
【分析】由题可知,爷爷做的篱笆中有三角形,三角形可以使篱笆更加稳固,不易变形,生活中有很多这样的例子,例如自行车的三角形车架、三角形房架、长方形门框的斜拉条、起重机的三角形吊臂车架等,都是利用了三角形的稳定性,起到了加固作用,据此即可解答。
【详解】爷爷给一块地围上篱笆,这样围十分牢固。依据的原理是三角形具有稳定性。
3. 周 360
【分析】根据题目要求将四个角撕下来,再拼在一起;锐角是大于0°小于90°的角,直角是等于90°的角,钝角是大于90°小于180°的角,平角是等于180°的角,周角是等于360°的角;据此解答。
【详解】根据分析如图:
所以把平行四边形的各个角撕下来拼在一起,拼成的角是周角,是360°。
4. 5 平行四边形
【分析】梯形的周长,就是梯形4条边的长度之和,而等腰梯形的两腰是相等的,用23减5再减8,所得的差就是两腰的和,再除以2即可求出腰长。如果将这个梯形的上底增加3厘米,那么此时的上底是8厘米,与下底相等,此时这个四边形就是平行四边形。
【详解】(23-5-8)÷2
=(18-8)÷2
=10÷2
=5(厘米)
一个等腰梯形的周长为23厘米,上底和下底分别为5厘米和8厘米,这个等腰梯形的腰长是5厘米;如果将这个梯形的上底增加3厘米,下底不变,会变成一个平行四边形。
5. 11 3
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边。这根小棒最长是(7+5-1)厘米,最短是(7-5+1)厘米。
【详解】7+5-1
=12-1
=11(厘米)
7-5+1
=2+1
=3(厘米)
气准备用小棒以首尾相接的方式围一个三角形,已经有7厘米和5厘米两根小棒,他还需要一根小棒(取整厘米数),这根小棒最长可以是11厘米,最短可以是3厘米。
6.11
【分析】三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答即可。
【详解】6+11=17 (厘米)
11-6=5 (厘米)
那么第三条边要大于5厘米小于17厘米,6~16厘米都可以,因此有11种可能。
7.锐角
【分析】三角形中三个角都小于90°,那么这个三角形为锐角三角形,三角形中有一个角为90°,那么这个三角形为直角三角形,三角形中有一个角大于90°,那么这个三角形为钝角三角形。
三角形的内角和为180°,用180°依次减去75°和63°,即可求出第三个角的度数,再根据三角形的三个角的度数的大小,判断出三角形是什么三角形即可。
【详解】180°-75°-63°
=105°-63°
=42°
90°>75°>63°>42°
所以一个三角形中,有一个角是75°,一个角是63°,按角的大小分,这个三角形是锐角三角形。
8. 120 等腰
【分析】根据三角形内角和为180°,等腰三角形的底角相同,用180°减去两个底角的度数,即可求出顶角的度数;等腰三角形的两个底角相等。据此解答即可。
【详解】180°-30°-30°=120°
红领巾是少先队员的标志,代表红旗的一角。一种红领巾的底角是,它的顶角是120,这是一个等腰三角形。
9.二
【分析】用圆规量出小棒的长度,再用三角板上的直角比一比,即可判断。
【详解】
第一组小棒:4cm、4cm、4cm
这是一个等边三角形;
第二组小棒:3cm、4cm、5cm
这是一个直角三角形;
第三组小棒:5cm、6cm、7cm
这是一个锐角三角形;
第四组小棒:4cm、4cm、5cm
这是一个等腰三角形。
所以,用上述四组小棒分别围一个三角形,可以围成一个直角三角形的是第二组小棒。
10. 稳定 2
【分析】三角形具有稳定性,由此解答即可;根据直角、平角的含义:等于90度的角是直角,等于180度的角是平角;据此即可解答。
【详解】三角形具有稳定性。1个平角等于2个直角。
11.√
【分析】两组对边分别平行的四边形是平行四边形。如下图:
由图可知,平行四边形的两组对边互相平行。
【详解】由分析可知,平行四边形的两组对边互相平行。
故答案为:√
12.×
【分析】等腰三角形有2条边相等,任意三角形的两边之和必须大于第三边,求出两边之和与第三边比较,满足三边关系的即可,把三条边的长度相加就能求出三角形的周长。
【详解】因为4+4<9,所以不符合三角形的三边关系,腰的长不能为4厘米,只能9厘米为腰长,底为4厘米。
9×2+4
=18+4
=22(厘米)
所以这个三角形的周长是22厘米,故原题说法错误。
故答案为:×
13.×
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点。而四边形具有不稳定性,又叫做易变形性,是指四边形边长确定,其形状、大小不能完全确定。由此解答此题即可。
【详解】三角形具有稳定性,但正方形具有不稳定性,所以原题说法错误。
故答案为:×
14.√
【分析】等腰三角形的两条腰长度相等。三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)。据此解答。
【详解】8.6厘米=8.6厘米,8.6+8.6=17.2(厘米),17.2厘米>16厘米,即这三条线段可以围成一个等腰三角形。原题说法正确。
故答案为:√
15.×
【分析】根据三角形内角和是180°,用180°减去两个已知角的度数,求出第三个角的度数,再判断三角形,据此解答。
【详解】180°-15°-85°
=165°-85°
=80°
最大角是85°,这个三角形为锐角三角形。
一个三角形中,其中两个角的度数分别是15°和85°,按角分,这是一个锐角三角形。
原题干说法错误。
故答案为:×
16.D
【分析】平行四边形对边平行且相等,对角相等,根据平行四边形的定义和判定方法直接解答。
【详解】只有②和④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点。
故答案为:D
17.A
【分析】锐角大于0°小于 90°、直角等于90°、钝角大于90°小于180°。
锐角三角形是指三角形的三个内角都是锐角的三角形。直角三角形是指有一个角为90°的三角形。梯形是指一组对边平行而另一组对边不平行的四边形。平行四边形是在同一平面内,两组对边分别平行的四边形。
根据图形露出角的大小可知,是一个钝角,因此这个图形可能是钝角三角形,也可能是平行四边形及梯形,据此解答。
【详解】因为露出的角是一个钝角,所以这个图形不可能是锐角三角形。
故答案为:A
18.C
【分析】三角形的内角和是180°;结合题意可知,三角形中的另一个角的度数=180°-其中两个角的度数和;大于90°且小于180°的角是钝角;三角形中,有一个角是钝角的三角形是钝角三角形。据此解答。
【详解】180°-80°=100°
100°>90°
则一个三角形中,其中两个角的和是80°,这个三角形是钝角三角形。
故答案为:C
19.B
【分析】根据各图形的特点进行判断:长方形有四条边,两组对边平行且相等,四个角都是直角;三角形由三条线段围成;平行四边形有四条边,两组对边分别平行且相等;梯形有四条边,只有一组对边平行;再按照顺序数出各图形的个数,先一个一个地数,再两个两个地数,再三个三个地数……,直到数出所有的个数;据此解答。
【详解】A. 一个一个地数有6个梯形,两个两个地数有7个梯形,三个三个地数有2个梯形,四个四个地数有2个梯形,六个六个地数有1个梯形,所以一共有6+7+2+2+1,即18个梯形;
B. 一个一个地数有3个三角形,两个两个地数有5个三角形,三个三个地数有1个三角形,四个四个地数有2个三角形,六个六个地数有1个三角形,所以一共有3+5+1+2+1,即12个三角形;
C. 一个一个地数有6个长方形,两个两个地数有7个长方形,三个三个地数有2个长方形,四个四个地数有2个长方形,六个六个地数有1个长方形,所以一共有6+7+2+2+1,即18个长方形;
D. 一个一个地数有6个平行四边形,两个两个地数有7个平行四边形,三个三个地数有2个平行四边形,四个四个地数有2个平行四边形,六个六个地数有1个平行四边形,所以一共有6+7+2+2+1,即18个平行四边形。
所以,数图形的结果跟其他三幅不一样的是。
故答案为:B
20.A
【分析】等腰三角形的特征是两条腰长度相等,所以用周长35厘米减去底边长是11厘米是两条腰的长度,再除以2是一条腰长。
【详解】(35-11)÷2
=24÷2
=12(厘米)
这个等腰三角形的其中一条腰长是12厘米。
故答案为:A
21.96°;34°
【分析】根据三角形内角和是180°,用180°减去已知的两个角的度数,即可求出未知角的度数。
【详解】180°-35°-49°
=145°-49°
=96°
180°-45°-101°
=135°-101°
=34°
左边三角形未知角的度数是96°,右边三角形未知角的度数是34°。
22.见详解
【分析】等腰三角形是指至少有两边相等的三角形。相等的两条边称为这个三角形的腰,另一边叫做底边。
梯形是指一组对边平行而另一组对边不平行的四边形。平行的两边叫做梯形的底边,长的一条底边叫下底,短的一条底边叫上底;不平行的两边叫腰。
平行四边形是在同一平面内,两组对边分别平行的四边形。
根据等腰三角形、梯形和平行四边形的特点,据此画图即可。
【详解】如图:
(答案不唯一)
23.不相信;理由见详解
【分析】根据题意,哥哥的两条腿长和一步长相当于三条线段。判断它们能否围成三角形,根据三角形的任意两边之和大于第三条边。
【详解】2米=200厘米
97+97<200
200+97>97
200+97>97
答:不相信,因为97厘米、97厘米、200厘米不能围成三角形,所以哥哥走一步不能迈2米。
24.见详解
【分析】要组成三角形,需要满足三角形的三边关系,即任意两边的长度和大于第三边,任意两边的长度差小于第三边,再根据所给的小棒长度进行组合判断即可。
【详解】①3厘米、3厘米、3厘米
3+3=6(厘米)
6>3
3-3=0(厘米)
3>0
所以3根3厘米的小棒可以组成三角形。
②3厘米、3厘米、4厘米
3+3=6(厘米)
6>4
4-3=1(厘米)
3>1
所以2根3厘米,1根4厘米的小棒可以组成三角形。
③3厘米、4厘米、6厘米
3+4=7(厘米)
7>6
6-3=3(厘米)
4>3
所以长分别为3厘米、4厘米、6厘米的小棒可以组成三角形。
答:可以组成三角形的组合为:3厘米、3厘米、3厘米;3厘米、3厘米、4厘米;3厘米、4厘米、6厘米。
25.两个角的度数分别是70°和40°或两个角的度数都是55°
【分析】在等腰三角形中,两个底角相等且三个内角之和为180°。已知等腰三角形中的一个角是70°,那么有两种情况。第一种,如果已知的那个角是底角,那么剩下的两个角分别是底角和顶角,也就是另一个底角也为70°。然后用180°减去两个底角的度数之和即可得到另一个顶角的度数。第二种,如果已知的那个角是顶角,那么可以用180°减去顶角的度数可以得到两个底角的度数之和。最后用除法即可求出另外两个底角的度数。
【详解】第一种:如果已知的那个角是底角,它的度数是70°,那么另一个底角的度数也是70°。
180°-(70°+70°)
=180°-140°
=40°
第二种:如果已知的那个角是顶角,它的度数是70°。
(180°-70°)÷2
=110°÷2
=55°
答:明明画的等腰三角形中另外两个角的度数分别是70°和40°或两个角的度数都是55°。
26.64米
【分析】观察图可以发现,菜地的有一边靠墙,要用篱笆把这块菜地围起来,只需要围另外3条边即可,将这三条边的长度相加,据此解答即可。
【详解】18+20+26
=38+26
=64(米)
答:至少要用篱笆64米。
27.20厘米
【分析】等边三角形的三条边都相等,先根据正方形的周长=边长×4,求出正方形的周长,即铁丝的长度,再除以3就是等边三角形的边长。
【详解】15×4÷3
=60÷3
=20(厘米)
答:三角形的边长是20厘米。
28.9分米
【分析】等边三角形的三条边的长度都相等,等腰三角形的两条腰长度相等。由题意得,一根铁丝正好围成一个边长为8分米的等边三角形,那么可以用8乘3算出这根铁丝的长度。如果用这根铁丝围成一个底边为6分米的等腰三角形,那么直接用这根铁丝的长度减去底边长即可算出两条腰的长度,再除以2即可算出一条腰的长度。
【详解】8×3=24(分米)
(24-6)÷2
=18÷2
=9(分米)
答:这个等腰三角形的一条腰长是9分米。
29.见详解
【分析】(1)三角形具有稳定性,具有稳固、坚定、耐压的特点。许多结构都利用了三角形的稳定性。比如房屋的屋顶架构,自行车的车架。
(2)平行四边形具有易变形的特性,在生活中,伸缩门就是利用平行四边形易变形的特性设计的,还有一些折叠晾衣架,其结构中部分采用平行四边形框架。
【详解】(1)由分析可知,自行车的设计利用了三角形的稳定性。(答案不唯一)
(2)由分析可知,移动门利用了平行四边形的易变形的特性。(答案不唯一)
30.见详解
【分析】长方形的对边平行且相等,长方形的四个角都是直角。平行四边形的对边平行且相等。只有一组对边平行的四边形是梯形,根据图形的特点,看看是哪两个图形拼成的指定形状。
【详解】(答案不唯一)①和⑤可以拼成长方形,②和③可以拼成平行四边形,⑦和⑧可以拼成梯形,①和⑤既可以拼成平行四边形也可以拼成梯形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元认识三角形和四边形(知识梳理+拔高训练)一
知识梳理
知识点一:图形分类
四边形容易变形,三角形具有稳定性。四边形和三角形的这些特性在生产和生活中有着广泛应用。
知识点二:三角形分类
判断一个三角形是锐角三角形、直角三角形还是钝角三角形,关键是看它最大的角,最大的角是哪类角,它就属于哪类三角形。
知识点三:三角形内角和
三角形的内角和不会随着三角形的大小、形状变化而发生变化,所有三角形的内角和都是180°。
知识点四:三角形边的关系
三角形任意两边之和大于第三边,任意两边之差小于第三边。
知识点五:四边形分类
四边形按照边的特点,可以把四边形分为:平行四边形、梯形和任意四边形三大类。正方形和长方形都是特殊的平行四边形。
拔高训练
一、填空题(共20分)
1.(2分)有一块等腰三角形的菜地,它的周长是236米,腰长83米,这块等腰三角形菜地的底边长是( )米。
2.(2分)爷爷给一块地围上篱笆,这样围十分牢固。依据的原理是三角形具有( )。
3.(2分)把平行四边形的各个角撕下来拼在一起,拼成的角是( )角,是( )°。
4.(2分)一个等腰梯形的周长为23厘米,上底和下底分别为5厘米和8厘米,这个等腰梯形的腰长是( )厘米;如果将这个梯形的上底增加3厘米,下底不变,会变成一个( )。
5.(2分)淘气准备用小棒以首尾相接的方式围一个三角形,已经有7厘米和5厘米两根小棒,他还需要一根小棒(取整厘米数),这根小棒最长可以是( )厘米,最短可以是( )厘米。
6.(2分)如果一个三角形两条边分别长6厘米和11厘米。如果第三条边的长度也为整数厘米数,第三条边的长度有( )种可能。
7.(2分)一个三角形中,有一个角是75°,一个角是63°,按角的大小分,这个三角形是( )三角形。
8.(2分)红领巾是少先队员的标志,代表红旗的一角。一种红领巾的底角是,它的顶角是( ),这是一个( )三角形。
9.(2分)第一组小棒:4cm、4cm、4cm;第二组小棒:3cm、4cm、5cm;第三组小棒:5cm、6cm、7cm;第四组小棒:4cm、4cm、5cm。用上述四组小棒分别围一个三角形,可以围成一个直角三角形的是第( )组小棒。(用上圆规画一画、试一试)。
10.(2分)三角形具有( )性。1个平角等于( )个直角。
二、判断题(共10分)
11.(2分)平行四边形的两组对边互相平行。( )
12.(2分)在一个等腰三角形中,有两条边的长度分别是4厘米和9厘米,这个三角形的周长可能是17厘米,也可能是22厘米。( )
13.(2分)三角形和正方形都具有稳定性。( )
14.(2分)长8.6厘米、8.6厘米、16厘米的三条线段可以围成一个等腰三角形。( )
15.(2分)一个三角形中,其中两个角的度数分别是15°和85°,按角分,这是一个钝角三角形。( )
三、选择题(共10分)
16.(2分)小敏不小心将一块玻璃打碎成了如图的4块。为了能在商店配到一块与原来相同的平行四边形玻璃,他只带了两块碎玻璃,其编号应该是( )。
A.①和② B.②和③ C.③和④ D.②和④
17.(2分)如图藏在云朵后面的图形不可能是( )。
A.锐角三角形 B.钝角三角形 C.梯形 D.平行四边形
18.(2分)一个三角形中,其中两个角的和是80°,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
19.(2分)下面四幅图中,按要求数图形的结果跟其他三幅不一样的是( )。
A. B.
C. D.
20.(2分)用一根35厘米长的铁丝恰好可以围成一个等腰三角形,已知这个等腰三角形的底边长是11厘米,则这个等腰三角形的其中一条腰长是( )厘米。
A.12 B.13 C.14 D.16
四、计算题(共6分)
21.(6分)计算如图各未知角的度数。
五、作图题(共6分)
22.(6分)在点子图上按要求画图。
六、解答题(共48分)
23.(6分)萌萌的哥哥身高为1.85米,体重为62千克,腿长约97厘米。萌萌说她哥哥走一步能迈2米,对于这种说法,你相信吗?请从数学角度解释理由。(用三角形三边关系解答)
24.(6分)从下面5根小棒中任意取出3根,摆出两种不同的三角形。(单位:厘米)
25.(6分)奇奇在数学课上画了一个等腰三角形,已知他画的等腰三角形中的一个角是。你知道他画的等腰三角形中另外两个角分别是多少度吗?
26.(6分)王大爷靠墙种一块菜地(如图),如果他想用篱笆把这块菜地围起来,至少要用篱笆多少米?
27.(6分)小明用一根铁丝刚好围成一个边长是15厘米的正方形,如果用这根铁丝围成一个等边三角形,三角形的边长是多少厘米?
28.(6分)一根铁丝正好围成一个边长为8分米的等边三角形。如果用这根铁丝围成一个底边为6分米的等腰三角形,那么这个等腰三角形的一条腰长是多少分米?
29.(6分)“数学来源于生活又运用于生活”,你能用所学的数学知识解释下面的生活现象吗?
30.(6分)拼一拼。
下面哪两个图形能拼成长方形、平行四边形、梯形?剪下附页3图3中的图形试一试。
参考答案
1.70
【分析】等腰三角形两条腰相等,底边=三角形周长-腰长×2,即可解答。
【详解】236-83×2
=236-166
=70(米)
故这块等腰三角形菜地的底边长是70米。
2.稳定性
【分析】由题可知,爷爷做的篱笆中有三角形,三角形可以使篱笆更加稳固,不易变形,生活中有很多这样的例子,例如自行车的三角形车架、三角形房架、长方形门框的斜拉条、起重机的三角形吊臂车架等,都是利用了三角形的稳定性,起到了加固作用,据此即可解答。
【详解】爷爷给一块地围上篱笆,这样围十分牢固。依据的原理是三角形具有稳定性。
3. 周 360
【分析】根据题目要求将四个角撕下来,再拼在一起;锐角是大于0°小于90°的角,直角是等于90°的角,钝角是大于90°小于180°的角,平角是等于180°的角,周角是等于360°的角;据此解答。
【详解】根据分析如图:
所以把平行四边形的各个角撕下来拼在一起,拼成的角是周角,是360°。
4. 5 平行四边形
【分析】梯形的周长,就是梯形4条边的长度之和,而等腰梯形的两腰是相等的,用23减5再减8,所得的差就是两腰的和,再除以2即可求出腰长。如果将这个梯形的上底增加3厘米,那么此时的上底是8厘米,与下底相等,此时这个四边形就是平行四边形。
【详解】(23-5-8)÷2
=(18-8)÷2
=10÷2
=5(厘米)
一个等腰梯形的周长为23厘米,上底和下底分别为5厘米和8厘米,这个等腰梯形的腰长是5厘米;如果将这个梯形的上底增加3厘米,下底不变,会变成一个平行四边形。
5. 11 3
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边。这根小棒最长是(7+5-1)厘米,最短是(7-5+1)厘米。
【详解】7+5-1
=12-1
=11(厘米)
7-5+1
=2+1
=3(厘米)
气准备用小棒以首尾相接的方式围一个三角形,已经有7厘米和5厘米两根小棒,他还需要一根小棒(取整厘米数),这根小棒最长可以是11厘米,最短可以是3厘米。
6.11
【分析】三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答即可。
【详解】6+11=17 (厘米)
11-6=5 (厘米)
那么第三条边要大于5厘米小于17厘米,6~16厘米都可以,因此有11种可能。
7.锐角
【分析】三角形中三个角都小于90°,那么这个三角形为锐角三角形,三角形中有一个角为90°,那么这个三角形为直角三角形,三角形中有一个角大于90°,那么这个三角形为钝角三角形。
三角形的内角和为180°,用180°依次减去75°和63°,即可求出第三个角的度数,再根据三角形的三个角的度数的大小,判断出三角形是什么三角形即可。
【详解】180°-75°-63°
=105°-63°
=42°
90°>75°>63°>42°
所以一个三角形中,有一个角是75°,一个角是63°,按角的大小分,这个三角形是锐角三角形。
8. 120 等腰
【分析】根据三角形内角和为180°,等腰三角形的底角相同,用180°减去两个底角的度数,即可求出顶角的度数;等腰三角形的两个底角相等。据此解答即可。
【详解】180°-30°-30°=120°
红领巾是少先队员的标志,代表红旗的一角。一种红领巾的底角是,它的顶角是120,这是一个等腰三角形。
9.二
【分析】用圆规量出小棒的长度,再用三角板上的直角比一比,即可判断。
【详解】
第一组小棒:4cm、4cm、4cm
这是一个等边三角形;
第二组小棒:3cm、4cm、5cm
这是一个直角三角形;
第三组小棒:5cm、6cm、7cm
这是一个锐角三角形;
第四组小棒:4cm、4cm、5cm
这是一个等腰三角形。
所以,用上述四组小棒分别围一个三角形,可以围成一个直角三角形的是第二组小棒。
10. 稳定 2
【分析】三角形具有稳定性,由此解答即可;根据直角、平角的含义:等于90度的角是直角,等于180度的角是平角;据此即可解答。
【详解】三角形具有稳定性。1个平角等于2个直角。
11.√
【分析】两组对边分别平行的四边形是平行四边形。如下图:
由图可知,平行四边形的两组对边互相平行。
【详解】由分析可知,平行四边形的两组对边互相平行。
故答案为:√
12.×
【分析】等腰三角形有2条边相等,任意三角形的两边之和必须大于第三边,求出两边之和与第三边比较,满足三边关系的即可,把三条边的长度相加就能求出三角形的周长。
【详解】因为4+4<9,所以不符合三角形的三边关系,腰的长不能为4厘米,只能9厘米为腰长,底为4厘米。
9×2+4
=18+4
=22(厘米)
所以这个三角形的周长是22厘米,故原题说法错误。
故答案为:×
13.×
【分析】三角形具有稳定性,有着稳固、坚定、耐压的特点。而四边形具有不稳定性,又叫做易变形性,是指四边形边长确定,其形状、大小不能完全确定。由此解答此题即可。
【详解】三角形具有稳定性,但正方形具有不稳定性,所以原题说法错误。
故答案为:×
14.√
【分析】等腰三角形的两条腰长度相等。三角形三边的关系:任意两边之和大于第三边(较短两边之和大于第三边)。据此解答。
【详解】8.6厘米=8.6厘米,8.6+8.6=17.2(厘米),17.2厘米>16厘米,即这三条线段可以围成一个等腰三角形。原题说法正确。
故答案为:√
15.×
【分析】根据三角形内角和是180°,用180°减去两个已知角的度数,求出第三个角的度数,再判断三角形,据此解答。
【详解】180°-15°-85°
=165°-85°
=80°
最大角是85°,这个三角形为锐角三角形。
一个三角形中,其中两个角的度数分别是15°和85°,按角分,这是一个锐角三角形。
原题干说法错误。
故答案为:×
16.D
【分析】平行四边形对边平行且相等,对角相等,根据平行四边形的定义和判定方法直接解答。
【详解】只有②和④两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点。
故答案为:D
17.A
【分析】锐角大于0°小于 90°、直角等于90°、钝角大于90°小于180°。
锐角三角形是指三角形的三个内角都是锐角的三角形。直角三角形是指有一个角为90°的三角形。梯形是指一组对边平行而另一组对边不平行的四边形。平行四边形是在同一平面内,两组对边分别平行的四边形。
根据图形露出角的大小可知,是一个钝角,因此这个图形可能是钝角三角形,也可能是平行四边形及梯形,据此解答。
【详解】因为露出的角是一个钝角,所以这个图形不可能是锐角三角形。
故答案为:A
18.C
【分析】三角形的内角和是180°;结合题意可知,三角形中的另一个角的度数=180°-其中两个角的度数和;大于90°且小于180°的角是钝角;三角形中,有一个角是钝角的三角形是钝角三角形。据此解答。
【详解】180°-80°=100°
100°>90°
则一个三角形中,其中两个角的和是80°,这个三角形是钝角三角形。
故答案为:C
19.B
【分析】根据各图形的特点进行判断:长方形有四条边,两组对边平行且相等,四个角都是直角;三角形由三条线段围成;平行四边形有四条边,两组对边分别平行且相等;梯形有四条边,只有一组对边平行;再按照顺序数出各图形的个数,先一个一个地数,再两个两个地数,再三个三个地数……,直到数出所有的个数;据此解答。
【详解】A. 一个一个地数有6个梯形,两个两个地数有7个梯形,三个三个地数有2个梯形,四个四个地数有2个梯形,六个六个地数有1个梯形,所以一共有6+7+2+2+1,即18个梯形;
B. 一个一个地数有3个三角形,两个两个地数有5个三角形,三个三个地数有1个三角形,四个四个地数有2个三角形,六个六个地数有1个三角形,所以一共有3+5+1+2+1,即12个三角形;
C. 一个一个地数有6个长方形,两个两个地数有7个长方形,三个三个地数有2个长方形,四个四个地数有2个长方形,六个六个地数有1个长方形,所以一共有6+7+2+2+1,即18个长方形;
D. 一个一个地数有6个平行四边形,两个两个地数有7个平行四边形,三个三个地数有2个平行四边形,四个四个地数有2个平行四边形,六个六个地数有1个平行四边形,所以一共有6+7+2+2+1,即18个平行四边形。
所以,数图形的结果跟其他三幅不一样的是。
故答案为:B
20.A
【分析】等腰三角形的特征是两条腰长度相等,所以用周长35厘米减去底边长是11厘米是两条腰的长度,再除以2是一条腰长。
【详解】(35-11)÷2
=24÷2
=12(厘米)
这个等腰三角形的其中一条腰长是12厘米。
故答案为:A
21.96°;34°
【分析】根据三角形内角和是180°,用180°减去已知的两个角的度数,即可求出未知角的度数。
【详解】180°-35°-49°
=145°-49°
=96°
180°-45°-101°
=135°-101°
=34°
左边三角形未知角的度数是96°,右边三角形未知角的度数是34°。
22.见详解
【分析】等腰三角形是指至少有两边相等的三角形。相等的两条边称为这个三角形的腰,另一边叫做底边。
梯形是指一组对边平行而另一组对边不平行的四边形。平行的两边叫做梯形的底边,长的一条底边叫下底,短的一条底边叫上底;不平行的两边叫腰。
平行四边形是在同一平面内,两组对边分别平行的四边形。
根据等腰三角形、梯形和平行四边形的特点,据此画图即可。
【详解】如图:
(答案不唯一)
23.不相信;理由见详解
【分析】根据题意,哥哥的两条腿长和一步长相当于三条线段。判断它们能否围成三角形,根据三角形的任意两边之和大于第三条边。
【详解】2米=200厘米
97+97<200
200+97>97
200+97>97
答:不相信,因为97厘米、97厘米、200厘米不能围成三角形,所以哥哥走一步不能迈2米。
24.见详解
【分析】要组成三角形,需要满足三角形的三边关系,即任意两边的长度和大于第三边,任意两边的长度差小于第三边,再根据所给的小棒长度进行组合判断即可。
【详解】①3厘米、3厘米、3厘米
3+3=6(厘米)
6>3
3-3=0(厘米)
3>0
所以3根3厘米的小棒可以组成三角形。
②3厘米、3厘米、4厘米
3+3=6(厘米)
6>4
4-3=1(厘米)
3>1
所以2根3厘米,1根4厘米的小棒可以组成三角形。
③3厘米、4厘米、6厘米
3+4=7(厘米)
7>6
6-3=3(厘米)
4>3
所以长分别为3厘米、4厘米、6厘米的小棒可以组成三角形。
答:可以组成三角形的组合为:3厘米、3厘米、3厘米;3厘米、3厘米、4厘米;3厘米、4厘米、6厘米。
25.两个角的度数分别是70°和40°或两个角的度数都是55°
【分析】在等腰三角形中,两个底角相等且三个内角之和为180°。已知等腰三角形中的一个角是70°,那么有两种情况。第一种,如果已知的那个角是底角,那么剩下的两个角分别是底角和顶角,也就是另一个底角也为70°。然后用180°减去两个底角的度数之和即可得到另一个顶角的度数。第二种,如果已知的那个角是顶角,那么可以用180°减去顶角的度数可以得到两个底角的度数之和。最后用除法即可求出另外两个底角的度数。
【详解】第一种:如果已知的那个角是底角,它的度数是70°,那么另一个底角的度数也是70°。
180°-(70°+70°)
=180°-140°
=40°
第二种:如果已知的那个角是顶角,它的度数是70°。
(180°-70°)÷2
=110°÷2
=55°
答:明明画的等腰三角形中另外两个角的度数分别是70°和40°或两个角的度数都是55°。
26.64米
【分析】观察图可以发现,菜地的有一边靠墙,要用篱笆把这块菜地围起来,只需要围另外3条边即可,将这三条边的长度相加,据此解答即可。
【详解】18+20+26
=38+26
=64(米)
答:至少要用篱笆64米。
27.20厘米
【分析】等边三角形的三条边都相等,先根据正方形的周长=边长×4,求出正方形的周长,即铁丝的长度,再除以3就是等边三角形的边长。
【详解】15×4÷3
=60÷3
=20(厘米)
答:三角形的边长是20厘米。
28.9分米
【分析】等边三角形的三条边的长度都相等,等腰三角形的两条腰长度相等。由题意得,一根铁丝正好围成一个边长为8分米的等边三角形,那么可以用8乘3算出这根铁丝的长度。如果用这根铁丝围成一个底边为6分米的等腰三角形,那么直接用这根铁丝的长度减去底边长即可算出两条腰的长度,再除以2即可算出一条腰的长度。
【详解】8×3=24(分米)
(24-6)÷2
=18÷2
=9(分米)
答:这个等腰三角形的一条腰长是9分米。
29.见详解
【分析】(1)三角形具有稳定性,具有稳固、坚定、耐压的特点。许多结构都利用了三角形的稳定性。比如房屋的屋顶架构,自行车的车架。
(2)平行四边形具有易变形的特性,在生活中,伸缩门就是利用平行四边形易变形的特性设计的,还有一些折叠晾衣架,其结构中部分采用平行四边形框架。
【详解】(1)由分析可知,自行车的设计利用了三角形的稳定性。(答案不唯一)
(2)由分析可知,移动门利用了平行四边形的易变形的特性。(答案不唯一)
30.见详解
【分析】长方形的对边平行且相等,长方形的四个角都是直角。平行四边形的对边平行且相等。只有一组对边平行的四边形是梯形,根据图形的特点,看看是哪两个图形拼成的指定形状。
【详解】(答案不唯一)①和⑤可以拼成长方形,②和③可以拼成平行四边形,⑦和⑧可以拼成梯形,①和⑤既可以拼成平行四边形也可以拼成梯形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
