第二单元观察物体(二)(知识梳理+拔高训练)一-2024-2025学年四年级数学下学期培优检测卷(人教版)
文档属性
| 名称 | 第二单元观察物体(二)(知识梳理+拔高训练)一-2024-2025学年四年级数学下学期培优检测卷(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 546.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 19:39:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二单元观察物体(二)(知识梳理+拔高训练)一
知识梳理
知识点一:从不同位置观察同一物体
从不同位置观察同一物体,看到的图形可能是不同的。
知识点二:从同一位置观察不同物体
不同形状的立体图形从同一位置进行观察,所看到的形状可能不同,也可能相同。
拔高训练
一、填空题(共20分)
1.(2分)如图,从( )面看到的形状是,从( )面能看到3个正方形。
2.(2分)下面的物体由( )个小正方体搭成,从它的前面和左面看到的图形是( )(“相同”或“不同”)的。
3.(2分)下面是从三个不同的方向看到的立体图形的形状,这个立体图形是由( )个小正方体组成的。
4.(2分)给添上一个同样大的小正方体,使其从上面看到的图形不变,有( )种摆法。
5.(2分)下面几何体从左面看到的图形不是的有( )。(填序号)
① ② ③ ④
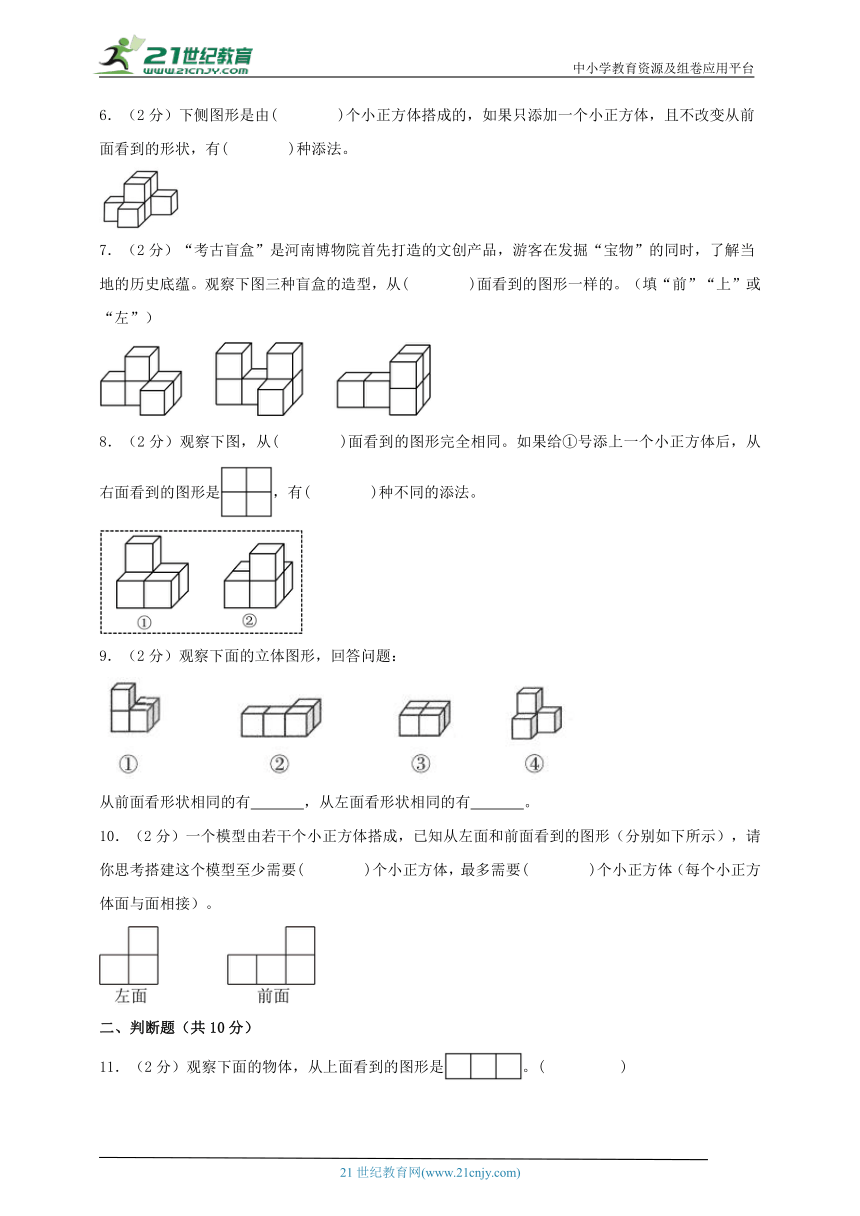
6.(2分)下侧图形是由( )个小正方体搭成的,如果只添加一个小正方体,且不改变从前面看到的形状,有( )种添法。
7.(2分)“考古盲盒”是河南博物院首先打造的文创产品,游客在发掘“宝物”的同时,了解当地的历史底蕴。观察下图三种盲盒的造型,从( )面看到的图形一样的。(填“前”“上”或“左”)
8.(2分)观察下图,从( )面看到的图形完全相同。如果给①号添上一个小正方体后,从右面看到的图形是,有( )种不同的添法。
9.(2分)观察下面的立体图形,回答问题:
从前面看形状相同的有 ,从左面看形状相同的有 。
10.(2分)一个模型由若干个小正方体搭成,已知从左面和前面看到的图形(分别如下所示),请你思考搭建这个模型至少需要( )个小正方体,最多需要( )个小正方体(每个小正方体面与面相接)。
二、判断题(共10分)
11.(2分)观察下面的物体,从上面看到的图形是。( )
12.(2分)从上面看这3个物体看到的图形是不同的。( )
13.(2分)分别从上面、前面和左面看,看到的图形都相同。( )
14.(2分)我们站在同一位置,最多能看到正方体状物体的3个面。( )
15.(2分)一个几何体,从上面看到的形状是,这个几何体一定是由3个小正方体组成的。( )
三、选择题(共10分)
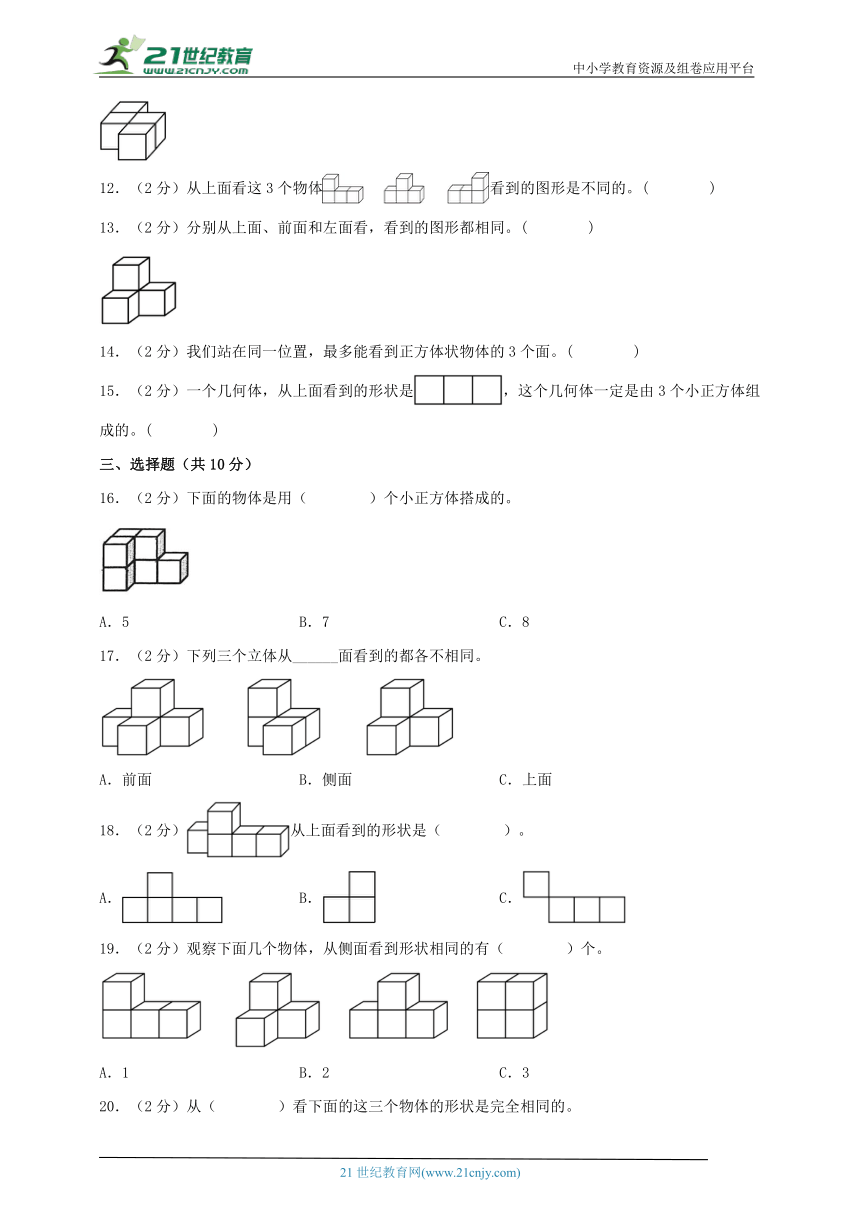
16.(2分)下面的物体是用( )个小正方体搭成的。
A.5 B.7 C.8
17.(2分)下列三个立体从______面看到的都各不相同。
A.前面 B.侧面 C.上面
18.(2分)从上面看到的形状是( )。
A. B. C.
19.(2分)观察下面几个物体,从侧面看到形状相同的有( )个。
A.1 B.2 C.3
20.(2分)从( )看下面的这三个物体的形状是完全相同的。
A.上面 B.右面 C.前面
四、连线题(共18分)
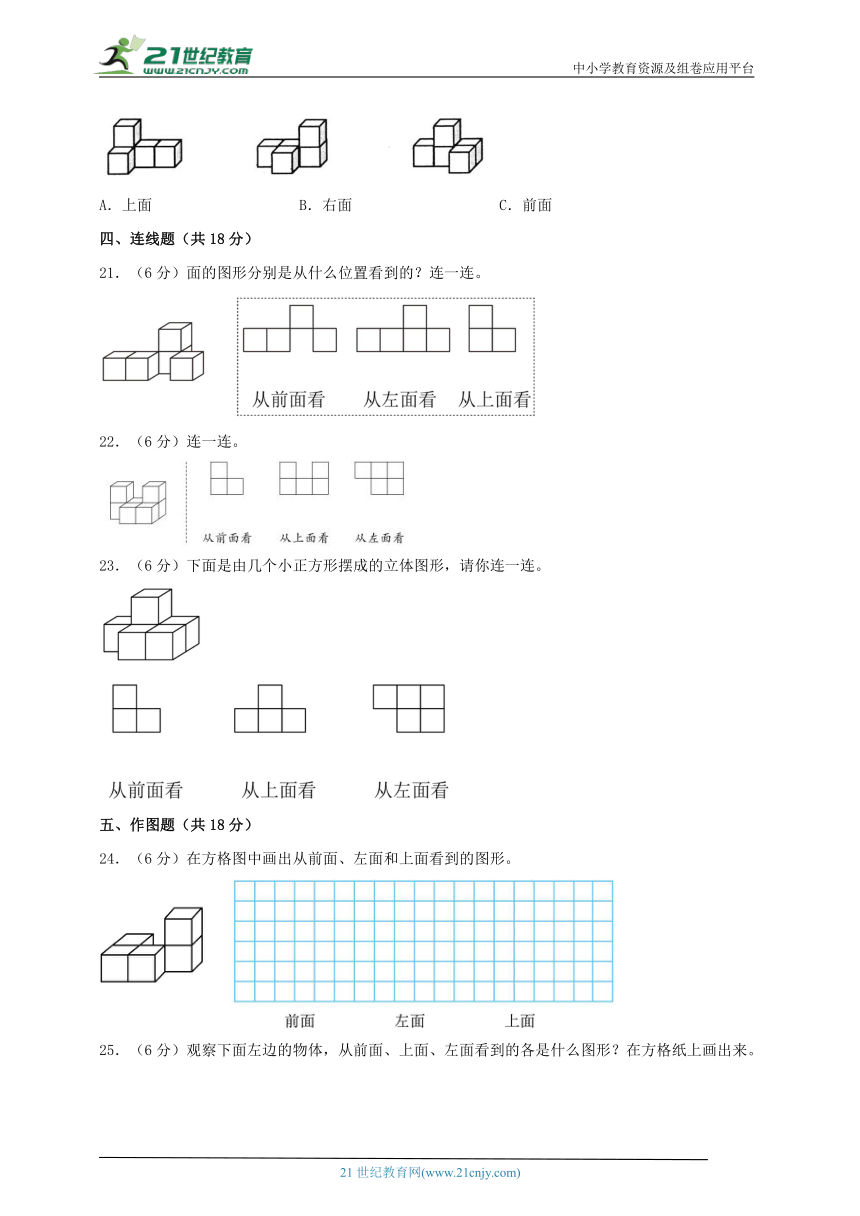
21.(6分)面的图形分别是从什么位置看到的?连一连。
22.(6分)连一连。
23.(6分)下面是由几个小正方形摆成的立体图形,请你连一连。
五、作图题(共18分)
24.(6分)在方格图中画出从前面、左面和上面看到的图形。
25.(6分)观察下面左边的物体,从前面、上面、左面看到的各是什么图形?在方格纸上画出来。
26.(6分)在方格中画出从前面、左面和上面看到的图形。
六、解答题(共24分)
27.(6分)一个立体图形从上面看的形状是,这个立体图形最下面一层摆了几个小正方体?如果这个立方体图形一共摆两层,最少有几个小正方体?最多可以摆几个小正方体?画出最多、最少两种情况的立体图形?
28.(6分)用4个相同的正方体搭一个立体图形,从上面看是,有( )种搭法。画出其中两种搭法从正面和右面看到的形状。
29.(6分)先摆一摆,再从前面、右面和上面看一看,从哪些面看到的图形完全相同?从哪些面看到的图形不同?
30.(6分)数一数,下面的物体是由多少个小正方体拼搭成的?
参考答案
1. 上 左
【分析】从正面看到的图形有2层,第一层有3个正方形,第二层有1个正方形,右对齐,共能看到4个正方形。
从上面看到的图形有2层,第一层有1个正方形,第二层有3个正方形,居中,共能看到4个正方形。
从左面看到的图形有2层,第一层有2个正方形,第二层有1个正方形,左对齐,共能看到3个正方形。
从右面看到的图形有2层,第一层有2个正方形,第二层有1个正方形,右对齐,共能看到3个正方形。
【详解】观察图形可知,从上面看到的形状是,从左面或者右面能看到3个正方形。
【点睛】本题主要考查从不同方向观察物体,培养学生的空间想象能力。
2. 2 相同
【分析】根据图形可知,此物体由2个小正方体搭成;从前面和左面看,都可看到1层,为2个小正方形,依此填空。
【详解】根据分析可知,此物体由2个小正方体搭成,从它的前面和左面看到的图形是相同的,都是。
【点睛】熟练掌握对三视图的认识是解答此题的关键。
3.6
【分析】根据从三个不同的方向看到的立体图形的形状,该几何体由6个小正方体拼成,下层5个,分3列,左面3个,中间和右面各1个,下齐;上层1个在右下的位置上。据此做题。
【详解】从三个不同的方向的观察可得下层5个,分3列,左面3个,中间和右面各1个,下齐;上层1个在右下的位置上,所以有3+1+1+1=6(个)
故由6个小正方体组成。
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
4.4
【分析】根据对三视图的认识可知,此图形从上面看,可看到2排,第1排可看到2个小正方形,第2排可看到2个小正方形,并且第2排右边的小正方形与第1排左边的小正方形对齐,因此要使从上面看到的图形不变,则这个小正方体只能放在已有的小正方体的上面,依此解答。
【详解】当这个同样大的小正方体放在第1排任意一个小正方体的上面,都能使这个图形从上面看到的图形不变,第1排一共有2个位置可放;当这个同样大的小正方体放在第2排任意一个小正方体的上面,也能使这个图形从上面看到的图形不变,第2排一共有2个位置可放。
2+2=4(种)
即给添上一个同样大的小正方体,使其从上面看到的图形不变,有4种摆法。
【点睛】熟练掌握对三视图的认识是解答此题的关键。
5.②
【分析】结合物体三视图的认识,只需要把这四个物体从左面看到的形状画出来,再判断即可。
【详解】
①物体的左视图为:
②物体的左视图为:
③物体的左视图为:
④物体的左视图为:
故只有②的左视图与其他几个物体不同。
6. 7 8
【分析】由图可知:下层有5个小正方体,上层有2个小正方体,共有7个小正方体。如果再添一个小正方体,从前面看到的形状不变,这个正方体可以放在已有小正方体的前面或者后面,有8种添法。
【详解】故这个图形是由7个小正方体搭成的,如果只添加一个小正方体,且不改变从前面看到的形状,有8种添法。
7.上
【分析】
观察,从前面看到,从上面看到,从左面看到;
观察,从前面看到,从上面看到,从左面看到;
观察,从前面看到,从上面看到,从左面看到。
【详解】观察三种盲盒的造型,从上面看到的图形一样的。
8. 上 2
【分析】
图①从前面看到的形状是,从左面看到的形状是,从右面看到的形状是;从上面看到的形状是;
图②从前面看到的形状是,从左面看到的形状是,从右面看到的形状是;从上面看到的形状是;
如下图,如果给图①的1或2位置添上一个小正方体后,从右面看到的图形是,有2种不同的添法。
【详解】
根据分析可知,从上面看到的图形完全相同。如果给①号添上一个小正方体后,从右面看到的图形是,有2种不同的添法。
9. ①④ ②③
【分析】从不同方向观察各立体图形,根据看到的图形进行解答。
从前面看,各图形的形状是:;
从左面看,各图形的形状是:。
【详解】根据分析可知:
从前面看形状相同的有①④;
从左面看形状相同的有②③。
10. 5 7
【分析】
根据观察物体的方法,结合从前面看到的图形可知,有2层,底层至少有3个小正方体,上层至少有1个小正方体,如图:再这个组合体的后面最多添加2个小正方体,从左面和前面看到的图形不变。。
【详解】在面面相连的情况下,至少需要5个小正方体,最多需要7个小正方体。
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
11.×
【分析】从上面看共有3行,上面的一行1个小正方形,下面的一行1个小正方形,中间的一行2个小正方形,据此判断即可。
【详解】
观察下面的物体,从上面看到的图形是。原题说法错误。
故答案为:×
12.×
【分析】根据物体三视图的认识和画法,分别画出3个物体从上面看到的图形,据此判断即可。
【详解】
从上面看:;
从上面看:;
从上面看:。
从上面看这3个物体看到的图形是相同的,原题说法错误。
故答案为:×
13.×
【分析】这个立体图形由4个相同的小正方体组成,从前面能看到3个正方形,分两层,上层1个,下层2个,左列对齐;从左面能看到3个正方形,分两层,上层1个,下层2个,左列对齐;从上面能看到3个正方形,分两层,上层2个,下层1个,左列对齐。
【详解】
分别从上面、前面和左面看,从前面、左面看到的图形相同,从前面、左面看到的图形与从上面看到的图形不同。
故答案为:×
14.√
【分析】从正方体的一面观察,只能看到1个面;从正方体两个面相交的那条线(棱)观察,只能看到正方体的2个面;从正方体三个面相交的那个点(顶点)观察,只能看到正方体的3个面。即站在任意位置观察同一正方体最少能看到正方体的1个面,最多能看到正方体的3个面。据此判断即可。
【详解】根据分析可知:我们站在同一位置,最多能看到正方体状物体的3个面,原题说法正确。
故答案为:√
15.×
【分析】
一个几何体,从上面看到的形状是,说明至少有三个小正方体横着排成一排。但在这三个小正方体的上面再添上小正方体,从上面看形状也是。这样的摆法有多种可能,据此解答即可。
【详解】
由分析知:从上面看,从上面看到的形状是,那么这个物体有可能是由三个小正方体组成,还有可能由更多的小正方体组成,这个几何体一定是由3个小正方体组成的,说法错误。
故答案为:×。
16.B
【分析】根据观察可知,从上往下看,第一行有3个小正方体,第二行有4个小正方体,3+4即为所求。
【详解】3+4=7(个)
下面的物体是用7个小正方体搭成的。
故答案为:B
17.C
【分析】逐项分析前面,侧面,上面看到的形状,比较后判断。
【详解】
第一幅图看到前面,右侧面,上面;
第二幅图看到前面,右侧面,上面;
第三幅图看到前面,右侧面,上面
分析可知三个立体从上面面看到的都各不相同。
故答案为:C
18.C
【分析】本题主要考查物体三视图的相关知识。从上面看时,可以看见两排正方形。上面一排,只有一个正方形(靠左)。下面一排,有三个正方形。据此解答。
【详解】
由分析得,从上面看到的形状是。
故答案为:C
19.C
【分析】根据题意,分别从侧面观察各选项的物体,看得到的图形是由几个小正方形组成的,它们的排列方式是怎样的,根据观察的结果进行解答。
【详解】从侧面看到的是。从侧面看到的是或。从侧面看到的是。从侧面看到的是。
观察下面几个物体,从侧面看到形状相同的有3个。
故答案为:C
20.B
【分析】第1个图,从上面看,能看到3列共4个面,第1列2个面,第2列1个面,与第1列最上面的面对齐,第3列1个面,与第2列的面对齐。
从右面看,能看到2列共3个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐。
从前面看,能看到3列共4个面,第1列2个面,第2列1个面,与第1列最下面的面对齐,第3列1个面,与第2列的面对齐。
第2个图,从上面看,能看到3列共4个面,第1列1个面,第2列2个面,最上面的面与第1列的面对齐,第3列1个面,与第2列最上面的面对齐。
从右面看,能看到2列共3个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐。
从前面看,能看到3列共4个面,第1列1个面,第2列1个面,与第1列的面对齐,第3列2个面,最下面的面与第2列的面对齐。
第3个图,从上面看,能看到3列共4个面,第1列1个面,第2列1个面,与第1列的面对齐,第3列2个面,最上面的面与第2列的面对齐。
从右面看,能看到2列共3个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐。
从前面看,能看到3列共4个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐,第3列1个面,与第2列最下面的面对齐。据此画图来解答。
【详解】
A.从上面看到的分别是:。
B.从右面看到的分别是:。
C.从前面看到的分别是:。
故答案为:B
21.见详解
【分析】从前面看,可以看到2层,第一层可看到4个小正方形,第二层可看到1个小正方形与第一层右边数第二个对齐;从上面看,第一层可看到3个小正方形,第二个小正方形后面空一个再与第三个连接,第二层可看到1个小正方形,在第一层空缺位置上面;从左面看,可看到2层,第一层可看到2个小正方形,第二层可看到1个小正方形,左齐;依此连线。
【详解】连线如下:
22.见详解
【分析】从前面看,图形是两层,最下层3个正方形,上面2个正方形(一个靠左,一个靠右);从上面看,图形是两层,最下层2个正方形靠右,上面3个正方形;从左面看,图形是两层,最下层2个正方形,上面1个正方形靠左;据此解答。
【详解】如图:
23.见详解
【分析】从前面看,是两行正方形,下面一行是3个正方形排成的一行,上面一行是1个正方形放中间;
从上面看,是两行正方形,最上面一行是3个正方形排成的一行,下面一行是2个正方形靠右放;
从左面看,是两行正方形,下面一行是2个正方形排成的一行,上面一行是1个正方形靠左放。据此连线即可。
【详解】见详解
连线如下:
24.见详解
【分析】从前面看,能看到4个正方形共3列,第1列1个正方形,第2列1个正方形,与第1列的正方形对齐,第3列2个正方形,最下面的正方形与第2列的正方形对齐;从左面看,能看到3个正方形共2列,第1列2个正方形,第2列1个正方形,且与第1列最下面的正方形对齐;从上面看,能看到4个正方形共3列,第1列2个正方形,第2列1个正方形,与第1列最下面的正方形对齐,第3列1个正方形,与第1列最上面的正方形对齐。
【详解】
25.见详解
【分析】从前面看,能看到3个面共2列,第1列2个面,第2列1个面,与第1列最下面的面对齐。从上面看,能看到3个面共2列,第1列1个面,第2列2个面,最上面的面与第1列的面对齐。从左面看,能看到3个面共2列,第1列2个面,第2列1个面,与第1列最下面的面对齐。
【详解】
26.见详解
【分析】从前面看到4个小正方形,分两层,下层3个,上层1个,右齐;
从左面看到3个小正方形,分两层,下层2个,上层1个,左齐;
从上面看到4个小正方形,分两层,上层3个,下层1个,居中;据此作图即可。
【详解】据分析作图如下:
27.4;5;8;图形见详解
【分析】从上面观察立体图形的平面图可以确定每个位置上的小正方体,根据这个平面图形摆立体图形最下面一层摆了4个小正方体;如果这个立方体图形一共摆两层,小正方体的数量最少,那么第二层最少有1个小正方体,小正方体的个数为(4+1)个;如果这个立方体图形一共摆两层,小正方体的数量最多,那么第二层最多有4个小正方体,小正方体的个数为(4+4)个;据此解答。
【详解】(1)如图所示,这个立体图形最下面一层摆了4个小正方体;
(2)如图所示,如果这个立方体图形一共摆两层,最少有5个小正方体;
(3)如图所示,如果这个立方体图形一共摆两层,最多可以摆8个小正方体。
【点睛】掌握根据平面图形确定立体图形小正方体个数的方法是解答题目的关键。
28.3;见详解
【分析】
从上面看是,说明这个几何体第一层有3个小正方体,第4个小正方体在这3个小正方体其中一个的上面。
【详解】这个立体图形有以下几种可能:
所以有3种搭法。
若选择的是上图中的第一种和第二种搭法,作图如下:
若选择的是上图中的第一种和第三种搭法,作图如下:
若选择的是上图中的第二种和第三种搭法,作图如下:
29.右面;前面和上面
【分析】根据物体三视图的认识和画法,画出这三个物体的三视图,据此判断从哪些面看到的图形完全相同;从哪些面看到的图形不同。
【详解】
从前面看:,从右面看:,从上面看:;
从前面看:,从右面看:,从上面看:;
从前面看:,从右面看:,从上面看:。
答:从右面看到的图形完全相同,从前面和上面看到的图形不同。
30.8个
【分析】在数小正方体的个数时,分层数,先数一数每层有多少个小正方体,最后将各层的个数加起来即可。
【详解】上面一层有3个正方体,下面一层有5个正方体。
(个)
答:下面的物体是由8个小正方体拼搭成的。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元观察物体(二)(知识梳理+拔高训练)一
知识梳理
知识点一:从不同位置观察同一物体
从不同位置观察同一物体,看到的图形可能是不同的。
知识点二:从同一位置观察不同物体
不同形状的立体图形从同一位置进行观察,所看到的形状可能不同,也可能相同。
拔高训练
一、填空题(共20分)
1.(2分)如图,从( )面看到的形状是,从( )面能看到3个正方形。
2.(2分)下面的物体由( )个小正方体搭成,从它的前面和左面看到的图形是( )(“相同”或“不同”)的。
3.(2分)下面是从三个不同的方向看到的立体图形的形状,这个立体图形是由( )个小正方体组成的。
4.(2分)给添上一个同样大的小正方体,使其从上面看到的图形不变,有( )种摆法。
5.(2分)下面几何体从左面看到的图形不是的有( )。(填序号)
① ② ③ ④
6.(2分)下侧图形是由( )个小正方体搭成的,如果只添加一个小正方体,且不改变从前面看到的形状,有( )种添法。
7.(2分)“考古盲盒”是河南博物院首先打造的文创产品,游客在发掘“宝物”的同时,了解当地的历史底蕴。观察下图三种盲盒的造型,从( )面看到的图形一样的。(填“前”“上”或“左”)
8.(2分)观察下图,从( )面看到的图形完全相同。如果给①号添上一个小正方体后,从右面看到的图形是,有( )种不同的添法。
9.(2分)观察下面的立体图形,回答问题:
从前面看形状相同的有 ,从左面看形状相同的有 。
10.(2分)一个模型由若干个小正方体搭成,已知从左面和前面看到的图形(分别如下所示),请你思考搭建这个模型至少需要( )个小正方体,最多需要( )个小正方体(每个小正方体面与面相接)。
二、判断题(共10分)
11.(2分)观察下面的物体,从上面看到的图形是。( )
12.(2分)从上面看这3个物体看到的图形是不同的。( )
13.(2分)分别从上面、前面和左面看,看到的图形都相同。( )
14.(2分)我们站在同一位置,最多能看到正方体状物体的3个面。( )
15.(2分)一个几何体,从上面看到的形状是,这个几何体一定是由3个小正方体组成的。( )
三、选择题(共10分)
16.(2分)下面的物体是用( )个小正方体搭成的。
A.5 B.7 C.8
17.(2分)下列三个立体从______面看到的都各不相同。
A.前面 B.侧面 C.上面
18.(2分)从上面看到的形状是( )。
A. B. C.
19.(2分)观察下面几个物体,从侧面看到形状相同的有( )个。
A.1 B.2 C.3
20.(2分)从( )看下面的这三个物体的形状是完全相同的。
A.上面 B.右面 C.前面
四、连线题(共18分)
21.(6分)面的图形分别是从什么位置看到的?连一连。
22.(6分)连一连。
23.(6分)下面是由几个小正方形摆成的立体图形,请你连一连。
五、作图题(共18分)
24.(6分)在方格图中画出从前面、左面和上面看到的图形。
25.(6分)观察下面左边的物体,从前面、上面、左面看到的各是什么图形?在方格纸上画出来。
26.(6分)在方格中画出从前面、左面和上面看到的图形。
六、解答题(共24分)
27.(6分)一个立体图形从上面看的形状是,这个立体图形最下面一层摆了几个小正方体?如果这个立方体图形一共摆两层,最少有几个小正方体?最多可以摆几个小正方体?画出最多、最少两种情况的立体图形?
28.(6分)用4个相同的正方体搭一个立体图形,从上面看是,有( )种搭法。画出其中两种搭法从正面和右面看到的形状。
29.(6分)先摆一摆,再从前面、右面和上面看一看,从哪些面看到的图形完全相同?从哪些面看到的图形不同?
30.(6分)数一数,下面的物体是由多少个小正方体拼搭成的?
参考答案
1. 上 左
【分析】从正面看到的图形有2层,第一层有3个正方形,第二层有1个正方形,右对齐,共能看到4个正方形。
从上面看到的图形有2层,第一层有1个正方形,第二层有3个正方形,居中,共能看到4个正方形。
从左面看到的图形有2层,第一层有2个正方形,第二层有1个正方形,左对齐,共能看到3个正方形。
从右面看到的图形有2层,第一层有2个正方形,第二层有1个正方形,右对齐,共能看到3个正方形。
【详解】观察图形可知,从上面看到的形状是,从左面或者右面能看到3个正方形。
【点睛】本题主要考查从不同方向观察物体,培养学生的空间想象能力。
2. 2 相同
【分析】根据图形可知,此物体由2个小正方体搭成;从前面和左面看,都可看到1层,为2个小正方形,依此填空。
【详解】根据分析可知,此物体由2个小正方体搭成,从它的前面和左面看到的图形是相同的,都是。
【点睛】熟练掌握对三视图的认识是解答此题的关键。
3.6
【分析】根据从三个不同的方向看到的立体图形的形状,该几何体由6个小正方体拼成,下层5个,分3列,左面3个,中间和右面各1个,下齐;上层1个在右下的位置上。据此做题。
【详解】从三个不同的方向的观察可得下层5个,分3列,左面3个,中间和右面各1个,下齐;上层1个在右下的位置上,所以有3+1+1+1=6(个)
故由6个小正方体组成。
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
4.4
【分析】根据对三视图的认识可知,此图形从上面看,可看到2排,第1排可看到2个小正方形,第2排可看到2个小正方形,并且第2排右边的小正方形与第1排左边的小正方形对齐,因此要使从上面看到的图形不变,则这个小正方体只能放在已有的小正方体的上面,依此解答。
【详解】当这个同样大的小正方体放在第1排任意一个小正方体的上面,都能使这个图形从上面看到的图形不变,第1排一共有2个位置可放;当这个同样大的小正方体放在第2排任意一个小正方体的上面,也能使这个图形从上面看到的图形不变,第2排一共有2个位置可放。
2+2=4(种)
即给添上一个同样大的小正方体,使其从上面看到的图形不变,有4种摆法。
【点睛】熟练掌握对三视图的认识是解答此题的关键。
5.②
【分析】结合物体三视图的认识,只需要把这四个物体从左面看到的形状画出来,再判断即可。
【详解】
①物体的左视图为:
②物体的左视图为:
③物体的左视图为:
④物体的左视图为:
故只有②的左视图与其他几个物体不同。
6. 7 8
【分析】由图可知:下层有5个小正方体,上层有2个小正方体,共有7个小正方体。如果再添一个小正方体,从前面看到的形状不变,这个正方体可以放在已有小正方体的前面或者后面,有8种添法。
【详解】故这个图形是由7个小正方体搭成的,如果只添加一个小正方体,且不改变从前面看到的形状,有8种添法。
7.上
【分析】
观察,从前面看到,从上面看到,从左面看到;
观察,从前面看到,从上面看到,从左面看到;
观察,从前面看到,从上面看到,从左面看到。
【详解】观察三种盲盒的造型,从上面看到的图形一样的。
8. 上 2
【分析】
图①从前面看到的形状是,从左面看到的形状是,从右面看到的形状是;从上面看到的形状是;
图②从前面看到的形状是,从左面看到的形状是,从右面看到的形状是;从上面看到的形状是;
如下图,如果给图①的1或2位置添上一个小正方体后,从右面看到的图形是,有2种不同的添法。
【详解】
根据分析可知,从上面看到的图形完全相同。如果给①号添上一个小正方体后,从右面看到的图形是,有2种不同的添法。
9. ①④ ②③
【分析】从不同方向观察各立体图形,根据看到的图形进行解答。
从前面看,各图形的形状是:;
从左面看,各图形的形状是:。
【详解】根据分析可知:
从前面看形状相同的有①④;
从左面看形状相同的有②③。
10. 5 7
【分析】
根据观察物体的方法,结合从前面看到的图形可知,有2层,底层至少有3个小正方体,上层至少有1个小正方体,如图:再这个组合体的后面最多添加2个小正方体,从左面和前面看到的图形不变。。
【详解】在面面相连的情况下,至少需要5个小正方体,最多需要7个小正方体。
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
11.×
【分析】从上面看共有3行,上面的一行1个小正方形,下面的一行1个小正方形,中间的一行2个小正方形,据此判断即可。
【详解】
观察下面的物体,从上面看到的图形是。原题说法错误。
故答案为:×
12.×
【分析】根据物体三视图的认识和画法,分别画出3个物体从上面看到的图形,据此判断即可。
【详解】
从上面看:;
从上面看:;
从上面看:。
从上面看这3个物体看到的图形是相同的,原题说法错误。
故答案为:×
13.×
【分析】这个立体图形由4个相同的小正方体组成,从前面能看到3个正方形,分两层,上层1个,下层2个,左列对齐;从左面能看到3个正方形,分两层,上层1个,下层2个,左列对齐;从上面能看到3个正方形,分两层,上层2个,下层1个,左列对齐。
【详解】
分别从上面、前面和左面看,从前面、左面看到的图形相同,从前面、左面看到的图形与从上面看到的图形不同。
故答案为:×
14.√
【分析】从正方体的一面观察,只能看到1个面;从正方体两个面相交的那条线(棱)观察,只能看到正方体的2个面;从正方体三个面相交的那个点(顶点)观察,只能看到正方体的3个面。即站在任意位置观察同一正方体最少能看到正方体的1个面,最多能看到正方体的3个面。据此判断即可。
【详解】根据分析可知:我们站在同一位置,最多能看到正方体状物体的3个面,原题说法正确。
故答案为:√
15.×
【分析】
一个几何体,从上面看到的形状是,说明至少有三个小正方体横着排成一排。但在这三个小正方体的上面再添上小正方体,从上面看形状也是。这样的摆法有多种可能,据此解答即可。
【详解】
由分析知:从上面看,从上面看到的形状是,那么这个物体有可能是由三个小正方体组成,还有可能由更多的小正方体组成,这个几何体一定是由3个小正方体组成的,说法错误。
故答案为:×。
16.B
【分析】根据观察可知,从上往下看,第一行有3个小正方体,第二行有4个小正方体,3+4即为所求。
【详解】3+4=7(个)
下面的物体是用7个小正方体搭成的。
故答案为:B
17.C
【分析】逐项分析前面,侧面,上面看到的形状,比较后判断。
【详解】
第一幅图看到前面,右侧面,上面;
第二幅图看到前面,右侧面,上面;
第三幅图看到前面,右侧面,上面
分析可知三个立体从上面面看到的都各不相同。
故答案为:C
18.C
【分析】本题主要考查物体三视图的相关知识。从上面看时,可以看见两排正方形。上面一排,只有一个正方形(靠左)。下面一排,有三个正方形。据此解答。
【详解】
由分析得,从上面看到的形状是。
故答案为:C
19.C
【分析】根据题意,分别从侧面观察各选项的物体,看得到的图形是由几个小正方形组成的,它们的排列方式是怎样的,根据观察的结果进行解答。
【详解】从侧面看到的是。从侧面看到的是或。从侧面看到的是。从侧面看到的是。
观察下面几个物体,从侧面看到形状相同的有3个。
故答案为:C
20.B
【分析】第1个图,从上面看,能看到3列共4个面,第1列2个面,第2列1个面,与第1列最上面的面对齐,第3列1个面,与第2列的面对齐。
从右面看,能看到2列共3个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐。
从前面看,能看到3列共4个面,第1列2个面,第2列1个面,与第1列最下面的面对齐,第3列1个面,与第2列的面对齐。
第2个图,从上面看,能看到3列共4个面,第1列1个面,第2列2个面,最上面的面与第1列的面对齐,第3列1个面,与第2列最上面的面对齐。
从右面看,能看到2列共3个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐。
从前面看,能看到3列共4个面,第1列1个面,第2列1个面,与第1列的面对齐,第3列2个面,最下面的面与第2列的面对齐。
第3个图,从上面看,能看到3列共4个面,第1列1个面,第2列1个面,与第1列的面对齐,第3列2个面,最上面的面与第2列的面对齐。
从右面看,能看到2列共3个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐。
从前面看,能看到3列共4个面,第1列1个面,第2列2个面,最下面的面与第1列的面对齐,第3列1个面,与第2列最下面的面对齐。据此画图来解答。
【详解】
A.从上面看到的分别是:。
B.从右面看到的分别是:。
C.从前面看到的分别是:。
故答案为:B
21.见详解
【分析】从前面看,可以看到2层,第一层可看到4个小正方形,第二层可看到1个小正方形与第一层右边数第二个对齐;从上面看,第一层可看到3个小正方形,第二个小正方形后面空一个再与第三个连接,第二层可看到1个小正方形,在第一层空缺位置上面;从左面看,可看到2层,第一层可看到2个小正方形,第二层可看到1个小正方形,左齐;依此连线。
【详解】连线如下:
22.见详解
【分析】从前面看,图形是两层,最下层3个正方形,上面2个正方形(一个靠左,一个靠右);从上面看,图形是两层,最下层2个正方形靠右,上面3个正方形;从左面看,图形是两层,最下层2个正方形,上面1个正方形靠左;据此解答。
【详解】如图:
23.见详解
【分析】从前面看,是两行正方形,下面一行是3个正方形排成的一行,上面一行是1个正方形放中间;
从上面看,是两行正方形,最上面一行是3个正方形排成的一行,下面一行是2个正方形靠右放;
从左面看,是两行正方形,下面一行是2个正方形排成的一行,上面一行是1个正方形靠左放。据此连线即可。
【详解】见详解
连线如下:
24.见详解
【分析】从前面看,能看到4个正方形共3列,第1列1个正方形,第2列1个正方形,与第1列的正方形对齐,第3列2个正方形,最下面的正方形与第2列的正方形对齐;从左面看,能看到3个正方形共2列,第1列2个正方形,第2列1个正方形,且与第1列最下面的正方形对齐;从上面看,能看到4个正方形共3列,第1列2个正方形,第2列1个正方形,与第1列最下面的正方形对齐,第3列1个正方形,与第1列最上面的正方形对齐。
【详解】
25.见详解
【分析】从前面看,能看到3个面共2列,第1列2个面,第2列1个面,与第1列最下面的面对齐。从上面看,能看到3个面共2列,第1列1个面,第2列2个面,最上面的面与第1列的面对齐。从左面看,能看到3个面共2列,第1列2个面,第2列1个面,与第1列最下面的面对齐。
【详解】
26.见详解
【分析】从前面看到4个小正方形,分两层,下层3个,上层1个,右齐;
从左面看到3个小正方形,分两层,下层2个,上层1个,左齐;
从上面看到4个小正方形,分两层,上层3个,下层1个,居中;据此作图即可。
【详解】据分析作图如下:
27.4;5;8;图形见详解
【分析】从上面观察立体图形的平面图可以确定每个位置上的小正方体,根据这个平面图形摆立体图形最下面一层摆了4个小正方体;如果这个立方体图形一共摆两层,小正方体的数量最少,那么第二层最少有1个小正方体,小正方体的个数为(4+1)个;如果这个立方体图形一共摆两层,小正方体的数量最多,那么第二层最多有4个小正方体,小正方体的个数为(4+4)个;据此解答。
【详解】(1)如图所示,这个立体图形最下面一层摆了4个小正方体;
(2)如图所示,如果这个立方体图形一共摆两层,最少有5个小正方体;
(3)如图所示,如果这个立方体图形一共摆两层,最多可以摆8个小正方体。
【点睛】掌握根据平面图形确定立体图形小正方体个数的方法是解答题目的关键。
28.3;见详解
【分析】
从上面看是,说明这个几何体第一层有3个小正方体,第4个小正方体在这3个小正方体其中一个的上面。
【详解】这个立体图形有以下几种可能:
所以有3种搭法。
若选择的是上图中的第一种和第二种搭法,作图如下:
若选择的是上图中的第一种和第三种搭法,作图如下:
若选择的是上图中的第二种和第三种搭法,作图如下:
29.右面;前面和上面
【分析】根据物体三视图的认识和画法,画出这三个物体的三视图,据此判断从哪些面看到的图形完全相同;从哪些面看到的图形不同。
【详解】
从前面看:,从右面看:,从上面看:;
从前面看:,从右面看:,从上面看:;
从前面看:,从右面看:,从上面看:。
答:从右面看到的图形完全相同,从前面和上面看到的图形不同。
30.8个
【分析】在数小正方体的个数时,分层数,先数一数每层有多少个小正方体,最后将各层的个数加起来即可。
【详解】上面一层有3个正方体,下面一层有5个正方体。
(个)
答:下面的物体是由8个小正方体拼搭成的。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
