第二单元因数和倍数(知识梳理+拔高训练)一-2024-2025学年五年级数学下学期培优检测卷(人教版)
文档属性
| 名称 | 第二单元因数和倍数(知识梳理+拔高训练)一-2024-2025学年五年级数学下学期培优检测卷(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 384.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 19:40:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二单元因数和倍数(知识梳理+拔高训练)一
知识梳理
知识点一:因数和倍数的意义
1.如果a×b=c(a、b、c都是不为0的整数),那么a是c的因数,b也是c的因数;c是a的倍数,c也是b的倍数。
2.倍数和因数是相互依存的。
注意:为了方便,在研究因数和倍数的时候,我们所说的数指的是自然数(一般不包括0)。
3.倍数的特征:一个数最小的倍数是它本身,没有最大的倍数。一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
4.找一个数的因数的方法:列乘法或除法算式。一个数的倍数的个数是无限的,最小的是它本身。
5.找一个数的倍数的方法: 用这个数依次乘非0自然数。一个数的倍数的个数是无限的,最小的是它本身。
知识点二:2、5、3的倍数的特征
1.个位上是0、2、4、6、8的数是2的倍数。
2.个位上是 0 或 5的数是 5 的倍数。
3.个位上是0的数是既是 2 的倍数又是 5 的倍数。
4.整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。0也是偶数。
5.一个数各位上的数的和是3的倍数,这个数就是3的倍数。
知识点三:质数、合数和奇偶性
1.一个数,如果只有1和它本身两个因数,那么这样的数叫做质数(或素数)。如2,3,5,7都是质数。
2.一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。如4,6,15,49都是合数。
3.1不是质数,也不是合数。
4.奇数±偶数=奇数,奇数×偶数=偶数,奇数±奇数=偶数,奇数×奇数=奇数,偶数±偶数=偶数,偶数×偶数=偶数。
拔高训练
一、填空题(共20分)
1.(2分)20名学生分成甲乙两个队参加义务劳动。如果甲队的人数是奇数,那么乙队的人数是( )数。(填奇、偶)
2.(2分)阳阳爸爸将家里的WiFi密码设置为ws6207□□,倒数第一位上的数既不是质数也不是合数,倒数第二位上的数是5的最小倍数。阳阳家的WiFi密码应该是ws6207( )。
3.(2分)从0,5,6,9这四个数字中取出三个,组成一个同时是2,3,5倍数的三位数,这个三位数最大是( )。
4.(2分)50名学生要分成甲、乙两队。如果甲队人数为奇数,则乙队人数为( )数;如果甲队人数为偶数,则乙队人数为( )数。
5.(2分)从0到9这10张数字卡片中任意选择4张组成一个四位数,使得这个四位数既能被3整除,又能被5整除。我组成的四位数是( )。
6.(2分)一个三位数,百位上的数是既不是质数也不是合数,十位上的数是最小的质数,个位上的数是最小的合数,这个三位数是( )。
7.(2分)一个六位数,各个数位上的数字从低位到高位依次是最小的偶数,最小的奇数,最小的质数,最小的合数,既是质数又是偶数,最大的一位数,这个六位数是( )。
8.(2分)近代数学三大难题之一的“哥德巴赫猜想”,是德国中学教师哥德巴赫在1742年首先提出的。一般提法是:每个不小于6的偶数都可表示为两个质数的和。如8=3+5,照这样想,10=( )+( ),18=( )+( )。
9.(2分)小红的年龄是2和7的倍数,妈妈的年龄是小红年龄的倍数,也是42的因数。小红的年龄是( ),妈妈的年龄是( )。
10.(2分)从0,5,7,8四个数中任意抽出3个,按要求组成不同的三位数。最大的偶数是( );既是3的倍数,又是5的倍数是( )。
二、判断题(共10分)
11.(2分)51的因数只有1和51,所以51是质数。( )
12.(2分)如果用2a(a是自然数)表示一个偶数,那么2a+1一定是奇数。( )
13.(2分)两个连续自然数的和不是质数就是合数。( )
14.(2分)除1以外,任何一个自然数的因数至少有2个。( )
15.(2分)一个数的倍数一定比它的因数大。( )
三、选择题(共10分)
16.(2分)从1,2,3,4,5,6,7这7张数字卡片中任意抽取一张,抽到( )的可能性最小。
A.质数 B.合数 C.奇数 D.偶数
17.(2分)在四位数15□□中的方框里填上数字,使它能同时被2、3、5整除,最多有( )种填法。
A.2 B.3 C.4 D.5
18.(2分)已知a、b均为自然数,且a÷2=b,则下面说法错误的是( )。
A.a是b的倍数 B.a是偶数 C.b是a的因数 D.b是2的倍数
19.(2分)一个质数与一个合数的和是11,它们的积不可能是 ( )。
A.10 B.24 C.28 D.18
20.(2分)有101个不同的正整数,在这101个数中有100个数互相不成倍数,但任意两数的和是2的倍数,任意三个数的和是3的倍数,任意四个数的和是4的倍数,任意六个数的和是6的倍数,则这101个数平均数的最小值可能是( )。
A.505 B.600 C.601 D.606
四、连线题(共6分)
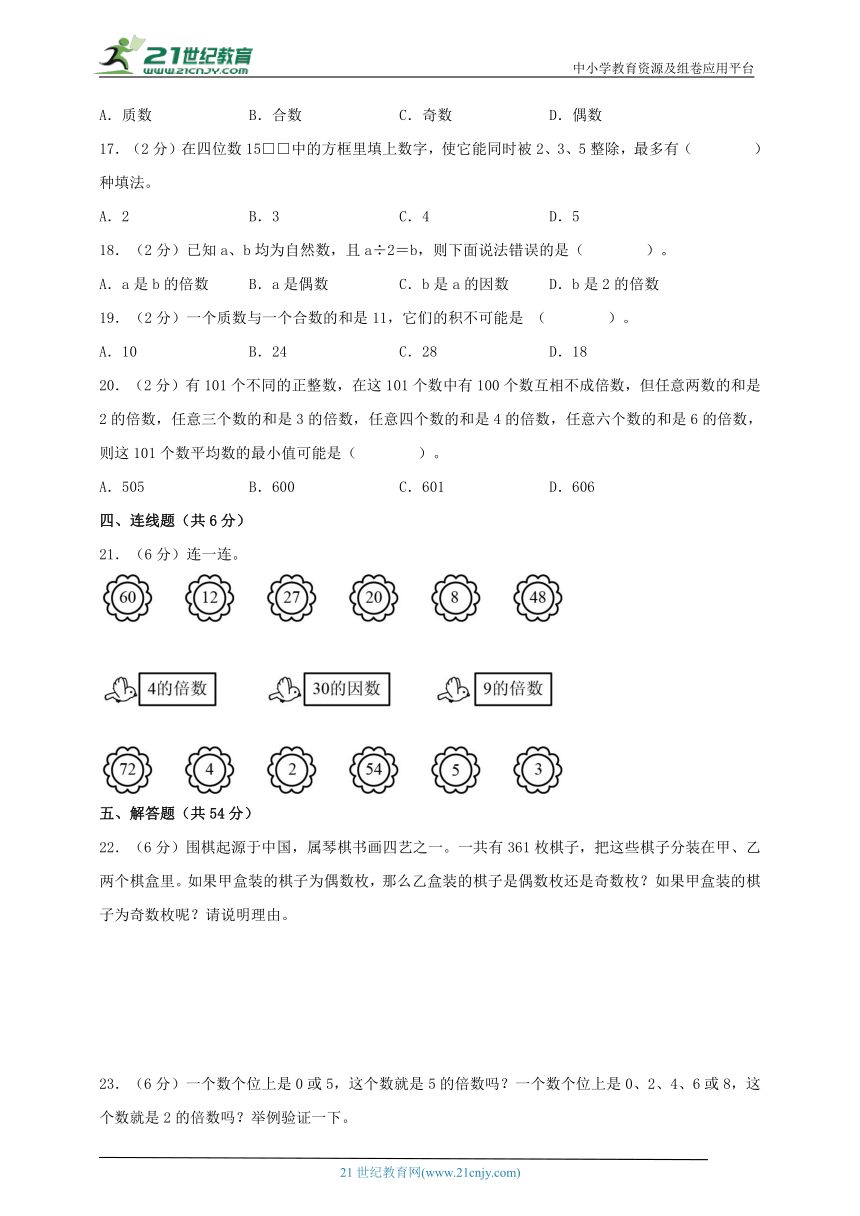
21.(6分)连一连。
五、解答题(共54分)
22.(6分)围棋起源于中国,属琴棋书画四艺之一。一共有361枚棋子,把这些棋子分装在甲、乙两个棋盒里。如果甲盒装的棋子为偶数枚,那么乙盒装的棋子是偶数枚还是奇数枚?如果甲盒装的棋子为奇数枚呢?请说明理由。
23.(6分)一个数个位上是0或5,这个数就是5的倍数吗?一个数个位上是0、2、4、6或8,这个数就是2的倍数吗?举例验证一下。
24.(6分)妈妈在花店买了一些马蹄莲和郁金香,店员说妈妈应付87元。按照下面的价格计算,店员说得对吗?
25.(6分)有78颗草莓,如果每5颗分给一个小朋友,能正好分完吗?如果每3颗分给一个小朋友,能正好分完吗?为什么?
26.(6分)一个长方形的长和宽均为质数,并且周长是64厘米。这个长方形的面积最多可以是多少?
27.(6分)育才小学五年级(1)班有36名同学排队表演学校集体舞,要使每行人数相等(每行不能是1人和36人),一共有多少种不同的排法?(可用表格或其它方法解决)
28.(6分)五(1)班学生在体育节进行队列表演,无论是3人一排、4人一排,还是6人一排,都正好站完。五(1)班学生的总人数在30~40之间,五(1)班有多少人?
29.(6分)有一个三位数,能同时是2和3的倍数,而且三个数位上的数字都是互不相同的质数,这个三位数可能是多少?
30.(6分)五(2)班部分学生参加全区数学竞赛,每张试卷有50道试题。评分标准是:答对一道给3分,不答的题每道给1分,答错一道扣1分。试问:这部分学生得分的总和能不能确定是奇数还是偶数?
参考答案
1.奇
【分析】根据运算性质,奇数+奇数=偶数,奇数+偶数=奇数,由于20是偶数,甲队的人数是奇数,只有再加个奇数才是偶数,所以乙队的人数是奇数,据此即可填空。
【详解】由分析可知:
20名学生分成甲乙两个队参加义务劳动。如果甲队的人数是奇数,那么乙队的人数是奇数。
2.51
【分析】1既不是质数也不是合数,则倒数第一位数字是1;5的最小倍数是5,则倒数第二位上的数是5,据此填空即可。
【详解】由分析可知:
阳阳家的WiFi密码应该是ws620751。
3.960
【分析】根据2、3、5倍数的特征,这个数的各位为0,且各数位数字之和是3的倍数,由此可知,十位和百位上的数的和是3的倍数,找出最大的数,即可解答。
【详解】根据分析可知,要想数最大,可以选9为百位,选6为十位;9+6=15,15是3的倍数。则这个数百位是9,十位是6,个位是0,这个数最大是960。
从0,5,6,9这四个数字中取出三个,组成一个同时是2,3,5倍数的三位数,这个三位数最大是960。
4. 奇 偶
【分析】奇数是指不能被2整除的数,偶数是指能被2整除的数。根据奇数、偶数的运算定理,奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数。据此可得出答案。
【详解】50名学生分为甲、乙两队,50为偶数。如果甲队人数为奇数,则奇数+奇数=偶数,则乙队人数为奇数;如果甲队人数为偶数,则偶数+偶数=偶数,乙队人数为偶数。
5.7320
【分析】既是3的倍数又是5的倍数的特征:个位上的数字是0或5,各个数位上的数字的和是3的倍数。这9个数中可以先确定个位,再确定其他三位,这4个数加起来的和是3倍数即可。
【详解】确定个位是0,2+3+7=12,12能被3整除。
则我组成的四位数是7320。(答案不唯一)
6.124
【分析】只有1和它本身两个因数的数叫做质数;除了1和它本身,还有其它因数的数叫做合数。1既不是质数也不是合数,最小的质数是2,最小的合数是4。据此解答。
【详解】通过分析可得:这个三位数是124。
7.924210
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。一个数,如果只有1和它本身两个因数,这样的数叫作质数;一个数,如果除了1和它本身还有别的因数,这样的数叫作合数;据此找出符合要求的数,再把相应数字写在这个六位数的相应数位上即可得解。
【详解】最小的偶数是0,最小的奇数是1,最小的质数是2,最小的合数是4,既是质数又是偶数的是2,最大的一位数是9,这个六位数是924210。
8. 7 3 11 7
【分析】是2的倍数的数叫偶数(0也是偶数);除了1和它本身以外不再有其他因数,这样的数叫质数;结合题目数字的大小找出比它小的质数,再计算填空。
【详解】比10小的质数有:2;3;5;7。
所以10=3+7
比18小的质数有:2;3;5;7;11;13;17。
可得18=11+17=13+5
9. 14 42
【分析】根据题意先找出42的因数,再从42的因数里面找出同时是2和7的倍数的数,小的数是小红的年龄,大的数是妈妈的年龄。
【详解】小红的年龄:需同时是2和7的倍数,即最小公倍数为14。
42的因数有1、2、3、6、7、14、21、42。
其中只有14和42是14的倍数。排除不合理数据(如14岁与小红同龄),妈妈的年龄应为42岁。
因此,小红14岁,妈妈42岁。
10. 870 870
【分析】2的倍数的特征:个位是0、2、4、6、8的数是2的倍数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。据此要使这个三位数最大,最大的数字8填入到它的百位上,它的个位上就只能是0了,它的十位上填入7即可;
既是3的倍数又是5的倍数的特征:个位上的数字是0或5,各个数位上的数字的和是3的倍数。据此这四个数中有7+5+0=12、8+7+0=15,12和15都是3的倍数,那么用7、5、0组成的三位数,只要个位上的数字是0或5,这个数既是3的倍数,又是5的倍数;据此写出这个数。
【详解】从0,5,7,8四个数中任意抽出3个,按要求组成不同的三位数。最大的偶数是870;既是3的倍数,又是5的倍数是870。(第二空答案不唯一)
11.×
【分析】根据求一个数的因数的方法,求出51的因数;
质数:一个数,只有1和它本身两个因数,这样的数叫做质数,据此解答。
【详解】51的因数有1,3,17,51;所以51不是质数。
原题干说法错误。
故答案为:×
12.√
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
偶数与奇数的运算性质,偶数+偶数=偶数,奇数+奇数=偶数,偶数+奇数=奇数。
【详解】根据偶数+奇数=奇数,可知:
如果用2a(a是自然数)表示一个偶数,那么2a+1一定是奇数。
原题说法正确。
故答案为:√
13.×
【分析】只用1和它本身两个因数的数是质数;除了1和它本身两个因数,还有其它因数的数是合数。1既不是质数,也不是合数。据此解答。
【详解】当这个两个连续自然数是0和1时,它们的和:0+1=1,1既不是质数也不是合数。题目说,两个连续自然数的和不是质数就是合数,这种说法是错误的。
故答案为:×
14.√
【分析】在乘法算式a×b=c(a、b、c均为非0的自然数)中,a、b就是c的因数,c就是a、b的倍数。在研究因数和倍数时,默认不考虑0;自然数中1的因数只有1;质数的因数只有1和本身2个因数;合数是除了1和本身外还有其它因数的数,至少3个因数。
【详解】由分析可知,除1以外,任何一个自然数不是质数就是合数,质数的因数有2个,合数的因数至少有3个,所以除1以外,任何一个自然数的因数至少有2个,该说法是正确的。
故答案为:√
15.×
【分析】根据因数和倍数的意义,一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数;由此解答即可。
【详解】一个数的最大因数是它本身,一个数的最小倍数也是它本身。例如,6的最小倍数是6,最大因数也是6,此时倍数和因数相等。因此,倍数不一定比因数大,原说法错误。
故答案为:×
16.B
【分析】除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。据此确定质数、合数、奇数和偶数的个数,比较,哪种数的个数最少,抽到哪种数的可能性就最小。
【详解】质数有2,3,5,7,共4个;合数有4,6,共2个;奇数有1、3、5、7,共4个;偶数有2,4,6,共3个,2<3<4,最少的是合数,抽到合数的可能性最小。
故答案为:B
17.C
【分析】根据2的倍数的特征,一个数的个位如果是偶数,这个数就是2的倍数;根据5的倍数的特征,一个数的个位是0或5,这个数就是5的倍数;个位上必需是0,才能满足既是2的倍数又是5的倍数,现在四位数变成15□0;然后再判断是不是3的倍数即可,3的倍数的特征是;各个数位上的和是3的倍数这个数就是3的倍数,把15□0中1、5、0加起来,即1+5+0=6,6是3的倍数,则分析6再加上10以内的几是3的倍数,□里就填几,然后数出填法有几种即可。
【详解】6+0=6
6+3=9
6+6=12
6+9=15
在□中可填0、3、6、9共4种填法。
故答案为:C
18.D
【分析】已知a、b均为自然数,且a÷2=b,则a=2b,我们就说a是2和b的倍数,2和b是a的因数。根据是2的倍数的数叫做偶数,即a是偶数。b是否是2的倍数,可举例说明,据此解答。
【详解】因为a÷2=b
所以a=2b
A.a是b的倍数,该说法正确。
B.a是偶数,该说法正确。
C.b是a的因数,该说法正确。
D.由 a÷2=b,若 ,则 ,此时b不是2的倍数。因此b不一定是2的倍数。该说法错误。
故答案为:D
19.A
【分析】除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。据此确定和是11的质数与合数的所有情况,再分别求积即可。
【详解】11=2+9=3+8=5+6=7+4
2×9=18;3×8=24;5×6=30;7×4=28
一个质数与一个合数的和是11,它们的积可能是18、24、30、28,不可能是10。
故答案为:A
20.C
【分析】个位上是0,2,4,6,8的数是2的倍数;如果一个数的各个数位上的数的和是3的倍数,那么这个数就是3的倍数,根据题目条件逐步分析得出这 100个数的特征,进而判断平均数的特点;
除以2的余数情况:因为任意两个数的和是2的倍数,两个数相加和是2的倍数,说明这两个数要么都是偶数(即除以2余数为0),要么都是奇数(即除以2余数为1)。又因为这100个数互相不成倍数,所以不能都是偶数(如果都是偶数,必然存在倍数关系),所以这100个数除以2的余数都为1。
除以3的余数情况:由于任意三个数的和是3的倍数,设这三个数分别为a、b、c,a+b+c=3k(k为整数)。根据余数的性质,a、b、c除以3的余数之和要是3的倍数。因为这100个数互相不成倍数,若有不同余数,就很难保证任意三个数和是3的倍数,所以这100个数除以3的余数都相同,又因为要满足和是3的倍数,所以余数只能为1(若余数为0,则这些数有倍数关系)。
除以4的余数情况:同理,任意四个数的和是4的倍数,设这四个数为m、n、p、q,m+n+p+q=4s(s为整数),根据余数性质,这100个数除以4的余数之和要是4的倍数。由于这100个数互相不成倍数,所以它们除以4的余数都相同,且为1(若余数为0或其他情况容易出现倍数关系不符合题意)。
除以6的余数情况:任意六个数的和是6的倍数,设这六个数为、、、、、,+++++=6t(t为整数),根据余数性质,这100个数除以6的余数之和要是6的倍数。因为这100个数互相不成倍数,所以它们除以6的余数都相同,且为1(若余数为0或其他情况,会出现倍数关系不符合要求)。
分析平均数:因为这100个数的平均数等于这100个数的总和除以100,而这100个数除以2、3、4、6余数都为1,那么它们的平均数除以2、3、4、6余数也都为1。
【详解】A.505÷2=252……1,505÷3=168……1,505÷4=126……1,505÷6=84……1,满足余数都为1;
B.600÷2=300,余数为0,不满足除以2余数为1,所以B选项错误;
C.601÷2=300……1,601÷3=200……1、601÷4=150……1、601÷6=100……1,满足余数都为1;
D.606÷2=303,余数为0,不满足除以2余数为1,所以D选项错误。
比较505和601,505<601,但题目问的是这101个数平均数的最小值,因为101个数中有100个数满足上述余数条件,当这100个数最小且满足余数条件时,平均数会最小,601比505更符合这101个数平均数最小的情况(因为505作为平均数时,可能无法满足101个数整体的条件,而601满足所有余数条件且能保证101个数整体的合理性)。
故答案为:C
【点睛】找出这100个数余数的特点,通过余数特点来判断平均数满足的条件是解题的关键。
21.见详解
【分析】4的倍数是指能被4整除的数,也就是说,这个数除以4的余数是0。可以通过用除法计算得解。
30能整除的数,就是30的因数,也就是说,30除以这个数的余数是0,可以通过用除法计算得解。
9的倍数是指能被4整除的数,也就是说,这个数除以9的余数是0。可以通过用除法计算得解。据此解答。
【详解】60÷4=15
12÷4=3
20÷4=5
8÷4=2
48÷4=12
72÷4=18
4÷4=1
30÷2=15
30÷5=6
30÷3=10
27÷9=3
72÷9=8
54÷9=6
连线如下:
22.见详解
【分析】根据奇偶数的运算性质:奇数±奇数=偶数;偶数±偶数=偶数;奇数±偶数=奇数;解答即可。
【详解】由分析可得:361是奇数,放进两个棋和就是将361分成两部分,即分成两个数。
如果一个数是偶数,那么另一个数一定是奇数;
如果一个数是奇数,那么另一个数一定是偶数。
答:如果甲盒装的棋子数为偶数,那么乙盒装的棋子数是奇数,如果甲盒装的棋子数为奇数那么乙盒装的棋子数是偶数。
23.是;是;举例见详解
【分析】5的倍数特征:个位上的数字是0或5的数是5的倍数。
2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。
【详解】一个数个位上是0或5,这个数就是5的倍数,如10、15、20、25、135……
一个数个位上是0、2、4、6或8,这个数就是2的倍数,如12、14、16、18、100……
24.不对
【分析】马蹄莲10元/枝,郁金香5元/枝,妈妈在花店买了一些马蹄莲和郁金香,则马蹄莲总钱数为10的倍数,郁金香总钱数是5的倍数。又由10=5×2,则马蹄莲总钱数为5的倍数,马蹄莲和郁金香总钱数是5的倍数;据此解答。
【详解】由分析可知:马蹄莲和郁金香的总钱数是5的倍数,而87的个位上是7,所以87不是5的倍数,所以店员说的不对。
25.见详解
【分析】个位上是0或5的数,是5的倍数;各位上数的和是3的倍数的数,是3的倍数,据此解题。
【详解】7+8=15
答:如果每5颗分给一个小朋友,不能正好分完,因为78的个位上是8,不符合5的倍数的特征。
如果每3颗分给一个小朋友,能正好分完,因为15是3的倍数,那么78也是3的倍数。
26.247平方厘米
【分析】根据长方体的周长=(长+宽)×2,用64÷2即可求出一条长和一条宽的和,也就是32厘米,一个数只有1和它本身两个因数,这个数叫做质数。32=3+29=13+19,所以长方形有2种情况,根据长方形的面积=长×宽,分别求出两种情况的面积,再比较即可。
【详解】64÷2=32(厘米)
32=3+29=13+19
3×29=87(平方厘米)
13×19=247(平方厘米)
87<247
答:这个长方形的面积最多可以是247平方厘米。
27.7种
【分析】找一个数的因数,可以利用乘法算式,按因数从小到大的顺序一组一组地找,这时,两个乘数都是积的因数。求出36有多少个因数,进而找出符合条件的排法即可。
【详解】36=1×36,排成1行或者36行,都不符合题意;
36=2×18,排成2行或者18行;
36=3×12,排成3行或者排成12行;
36=4×9,排成4行或者排成9行;
36=6×6,排成6行。
答:一共有7种不同的排法。
28.36人
【分析】根据题意,五(1)班的人数同时是3、4、6的倍数,用列举法找出3、4、6的倍数,并且保证人数在30~40之间,据此解答。
【详解】3的倍数:3、6、9、12、15、18、21、24、27、30、33、36、39…
4的倍数:4、8、12、16、20、24、28、32、36、40…
6的倍数:6、12、18、24、30、36、42…
所以36同时是3、4、6的倍数,且在30~40之间。
答:五(1)班有36人。
29.372
【分析】既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。除了1和它本身以外不再有其他因数,这样的数叫质数。
【详解】能同时是2和3的倍数,个位上的数字是0、2、4、6、8,质数有2;
10以内的质数有:2、3、5、7,2如果在个位,百位和十位能选择的数是3和7。
答:这个三位数可能是372或732。
30.能确定是偶数
【分析】根据题意,可以设每人答对a道,答错b道,则不答的题有(50-a-b)道;那么答对的题的得分是3a分,不答的题的得分是1×(50-a-b)分,答错的题的得分是(1×b)分,再相加,即是每人的总得分;然后分析这个总分数是奇数还是偶数,设这部分学生人数是偶数或奇数,根据奇数与偶数的运算性质确定这部分学生得分的总和能否确定是偶数还是奇数。
奇数和偶数的运算性质:
偶数+偶数=偶数,奇数+奇数=偶数,奇数+偶数=奇数;
奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数。
【详解】设每人答对a道,答错b道,则不答的题有(50-a-b)道,那么每人的得分是:
3×a+1×(50-a-b)-1×b
=3a+50-a-b-b
=(2a-2b+50)(分)
无论a、b是奇数还是偶数,2a、2b都是偶数,50也是偶数,偶数-偶数=偶数,偶数+偶数=偶数,所以(2a-2b+50)是偶数,即每人的得分是偶数。
如果这部分学生人数是偶数,则偶数×偶数=偶数;
如果这部分学生人数是奇数,则偶数×奇数=偶数。
答:这部分学生得分的总和能确定是偶数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元因数和倍数(知识梳理+拔高训练)一
知识梳理
知识点一:因数和倍数的意义
1.如果a×b=c(a、b、c都是不为0的整数),那么a是c的因数,b也是c的因数;c是a的倍数,c也是b的倍数。
2.倍数和因数是相互依存的。
注意:为了方便,在研究因数和倍数的时候,我们所说的数指的是自然数(一般不包括0)。
3.倍数的特征:一个数最小的倍数是它本身,没有最大的倍数。一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
4.找一个数的因数的方法:列乘法或除法算式。一个数的倍数的个数是无限的,最小的是它本身。
5.找一个数的倍数的方法: 用这个数依次乘非0自然数。一个数的倍数的个数是无限的,最小的是它本身。
知识点二:2、5、3的倍数的特征
1.个位上是0、2、4、6、8的数是2的倍数。
2.个位上是 0 或 5的数是 5 的倍数。
3.个位上是0的数是既是 2 的倍数又是 5 的倍数。
4.整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。0也是偶数。
5.一个数各位上的数的和是3的倍数,这个数就是3的倍数。
知识点三:质数、合数和奇偶性
1.一个数,如果只有1和它本身两个因数,那么这样的数叫做质数(或素数)。如2,3,5,7都是质数。
2.一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。如4,6,15,49都是合数。
3.1不是质数,也不是合数。
4.奇数±偶数=奇数,奇数×偶数=偶数,奇数±奇数=偶数,奇数×奇数=奇数,偶数±偶数=偶数,偶数×偶数=偶数。
拔高训练
一、填空题(共20分)
1.(2分)20名学生分成甲乙两个队参加义务劳动。如果甲队的人数是奇数,那么乙队的人数是( )数。(填奇、偶)
2.(2分)阳阳爸爸将家里的WiFi密码设置为ws6207□□,倒数第一位上的数既不是质数也不是合数,倒数第二位上的数是5的最小倍数。阳阳家的WiFi密码应该是ws6207( )。
3.(2分)从0,5,6,9这四个数字中取出三个,组成一个同时是2,3,5倍数的三位数,这个三位数最大是( )。
4.(2分)50名学生要分成甲、乙两队。如果甲队人数为奇数,则乙队人数为( )数;如果甲队人数为偶数,则乙队人数为( )数。
5.(2分)从0到9这10张数字卡片中任意选择4张组成一个四位数,使得这个四位数既能被3整除,又能被5整除。我组成的四位数是( )。
6.(2分)一个三位数,百位上的数是既不是质数也不是合数,十位上的数是最小的质数,个位上的数是最小的合数,这个三位数是( )。
7.(2分)一个六位数,各个数位上的数字从低位到高位依次是最小的偶数,最小的奇数,最小的质数,最小的合数,既是质数又是偶数,最大的一位数,这个六位数是( )。
8.(2分)近代数学三大难题之一的“哥德巴赫猜想”,是德国中学教师哥德巴赫在1742年首先提出的。一般提法是:每个不小于6的偶数都可表示为两个质数的和。如8=3+5,照这样想,10=( )+( ),18=( )+( )。
9.(2分)小红的年龄是2和7的倍数,妈妈的年龄是小红年龄的倍数,也是42的因数。小红的年龄是( ),妈妈的年龄是( )。
10.(2分)从0,5,7,8四个数中任意抽出3个,按要求组成不同的三位数。最大的偶数是( );既是3的倍数,又是5的倍数是( )。
二、判断题(共10分)
11.(2分)51的因数只有1和51,所以51是质数。( )
12.(2分)如果用2a(a是自然数)表示一个偶数,那么2a+1一定是奇数。( )
13.(2分)两个连续自然数的和不是质数就是合数。( )
14.(2分)除1以外,任何一个自然数的因数至少有2个。( )
15.(2分)一个数的倍数一定比它的因数大。( )
三、选择题(共10分)
16.(2分)从1,2,3,4,5,6,7这7张数字卡片中任意抽取一张,抽到( )的可能性最小。
A.质数 B.合数 C.奇数 D.偶数
17.(2分)在四位数15□□中的方框里填上数字,使它能同时被2、3、5整除,最多有( )种填法。
A.2 B.3 C.4 D.5
18.(2分)已知a、b均为自然数,且a÷2=b,则下面说法错误的是( )。
A.a是b的倍数 B.a是偶数 C.b是a的因数 D.b是2的倍数
19.(2分)一个质数与一个合数的和是11,它们的积不可能是 ( )。
A.10 B.24 C.28 D.18
20.(2分)有101个不同的正整数,在这101个数中有100个数互相不成倍数,但任意两数的和是2的倍数,任意三个数的和是3的倍数,任意四个数的和是4的倍数,任意六个数的和是6的倍数,则这101个数平均数的最小值可能是( )。
A.505 B.600 C.601 D.606
四、连线题(共6分)
21.(6分)连一连。
五、解答题(共54分)
22.(6分)围棋起源于中国,属琴棋书画四艺之一。一共有361枚棋子,把这些棋子分装在甲、乙两个棋盒里。如果甲盒装的棋子为偶数枚,那么乙盒装的棋子是偶数枚还是奇数枚?如果甲盒装的棋子为奇数枚呢?请说明理由。
23.(6分)一个数个位上是0或5,这个数就是5的倍数吗?一个数个位上是0、2、4、6或8,这个数就是2的倍数吗?举例验证一下。
24.(6分)妈妈在花店买了一些马蹄莲和郁金香,店员说妈妈应付87元。按照下面的价格计算,店员说得对吗?
25.(6分)有78颗草莓,如果每5颗分给一个小朋友,能正好分完吗?如果每3颗分给一个小朋友,能正好分完吗?为什么?
26.(6分)一个长方形的长和宽均为质数,并且周长是64厘米。这个长方形的面积最多可以是多少?
27.(6分)育才小学五年级(1)班有36名同学排队表演学校集体舞,要使每行人数相等(每行不能是1人和36人),一共有多少种不同的排法?(可用表格或其它方法解决)
28.(6分)五(1)班学生在体育节进行队列表演,无论是3人一排、4人一排,还是6人一排,都正好站完。五(1)班学生的总人数在30~40之间,五(1)班有多少人?
29.(6分)有一个三位数,能同时是2和3的倍数,而且三个数位上的数字都是互不相同的质数,这个三位数可能是多少?
30.(6分)五(2)班部分学生参加全区数学竞赛,每张试卷有50道试题。评分标准是:答对一道给3分,不答的题每道给1分,答错一道扣1分。试问:这部分学生得分的总和能不能确定是奇数还是偶数?
参考答案
1.奇
【分析】根据运算性质,奇数+奇数=偶数,奇数+偶数=奇数,由于20是偶数,甲队的人数是奇数,只有再加个奇数才是偶数,所以乙队的人数是奇数,据此即可填空。
【详解】由分析可知:
20名学生分成甲乙两个队参加义务劳动。如果甲队的人数是奇数,那么乙队的人数是奇数。
2.51
【分析】1既不是质数也不是合数,则倒数第一位数字是1;5的最小倍数是5,则倒数第二位上的数是5,据此填空即可。
【详解】由分析可知:
阳阳家的WiFi密码应该是ws620751。
3.960
【分析】根据2、3、5倍数的特征,这个数的各位为0,且各数位数字之和是3的倍数,由此可知,十位和百位上的数的和是3的倍数,找出最大的数,即可解答。
【详解】根据分析可知,要想数最大,可以选9为百位,选6为十位;9+6=15,15是3的倍数。则这个数百位是9,十位是6,个位是0,这个数最大是960。
从0,5,6,9这四个数字中取出三个,组成一个同时是2,3,5倍数的三位数,这个三位数最大是960。
4. 奇 偶
【分析】奇数是指不能被2整除的数,偶数是指能被2整除的数。根据奇数、偶数的运算定理,奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数。据此可得出答案。
【详解】50名学生分为甲、乙两队,50为偶数。如果甲队人数为奇数,则奇数+奇数=偶数,则乙队人数为奇数;如果甲队人数为偶数,则偶数+偶数=偶数,乙队人数为偶数。
5.7320
【分析】既是3的倍数又是5的倍数的特征:个位上的数字是0或5,各个数位上的数字的和是3的倍数。这9个数中可以先确定个位,再确定其他三位,这4个数加起来的和是3倍数即可。
【详解】确定个位是0,2+3+7=12,12能被3整除。
则我组成的四位数是7320。(答案不唯一)
6.124
【分析】只有1和它本身两个因数的数叫做质数;除了1和它本身,还有其它因数的数叫做合数。1既不是质数也不是合数,最小的质数是2,最小的合数是4。据此解答。
【详解】通过分析可得:这个三位数是124。
7.924210
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。一个数,如果只有1和它本身两个因数,这样的数叫作质数;一个数,如果除了1和它本身还有别的因数,这样的数叫作合数;据此找出符合要求的数,再把相应数字写在这个六位数的相应数位上即可得解。
【详解】最小的偶数是0,最小的奇数是1,最小的质数是2,最小的合数是4,既是质数又是偶数的是2,最大的一位数是9,这个六位数是924210。
8. 7 3 11 7
【分析】是2的倍数的数叫偶数(0也是偶数);除了1和它本身以外不再有其他因数,这样的数叫质数;结合题目数字的大小找出比它小的质数,再计算填空。
【详解】比10小的质数有:2;3;5;7。
所以10=3+7
比18小的质数有:2;3;5;7;11;13;17。
可得18=11+17=13+5
9. 14 42
【分析】根据题意先找出42的因数,再从42的因数里面找出同时是2和7的倍数的数,小的数是小红的年龄,大的数是妈妈的年龄。
【详解】小红的年龄:需同时是2和7的倍数,即最小公倍数为14。
42的因数有1、2、3、6、7、14、21、42。
其中只有14和42是14的倍数。排除不合理数据(如14岁与小红同龄),妈妈的年龄应为42岁。
因此,小红14岁,妈妈42岁。
10. 870 870
【分析】2的倍数的特征:个位是0、2、4、6、8的数是2的倍数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。据此要使这个三位数最大,最大的数字8填入到它的百位上,它的个位上就只能是0了,它的十位上填入7即可;
既是3的倍数又是5的倍数的特征:个位上的数字是0或5,各个数位上的数字的和是3的倍数。据此这四个数中有7+5+0=12、8+7+0=15,12和15都是3的倍数,那么用7、5、0组成的三位数,只要个位上的数字是0或5,这个数既是3的倍数,又是5的倍数;据此写出这个数。
【详解】从0,5,7,8四个数中任意抽出3个,按要求组成不同的三位数。最大的偶数是870;既是3的倍数,又是5的倍数是870。(第二空答案不唯一)
11.×
【分析】根据求一个数的因数的方法,求出51的因数;
质数:一个数,只有1和它本身两个因数,这样的数叫做质数,据此解答。
【详解】51的因数有1,3,17,51;所以51不是质数。
原题干说法错误。
故答案为:×
12.√
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
偶数与奇数的运算性质,偶数+偶数=偶数,奇数+奇数=偶数,偶数+奇数=奇数。
【详解】根据偶数+奇数=奇数,可知:
如果用2a(a是自然数)表示一个偶数,那么2a+1一定是奇数。
原题说法正确。
故答案为:√
13.×
【分析】只用1和它本身两个因数的数是质数;除了1和它本身两个因数,还有其它因数的数是合数。1既不是质数,也不是合数。据此解答。
【详解】当这个两个连续自然数是0和1时,它们的和:0+1=1,1既不是质数也不是合数。题目说,两个连续自然数的和不是质数就是合数,这种说法是错误的。
故答案为:×
14.√
【分析】在乘法算式a×b=c(a、b、c均为非0的自然数)中,a、b就是c的因数,c就是a、b的倍数。在研究因数和倍数时,默认不考虑0;自然数中1的因数只有1;质数的因数只有1和本身2个因数;合数是除了1和本身外还有其它因数的数,至少3个因数。
【详解】由分析可知,除1以外,任何一个自然数不是质数就是合数,质数的因数有2个,合数的因数至少有3个,所以除1以外,任何一个自然数的因数至少有2个,该说法是正确的。
故答案为:√
15.×
【分析】根据因数和倍数的意义,一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数;由此解答即可。
【详解】一个数的最大因数是它本身,一个数的最小倍数也是它本身。例如,6的最小倍数是6,最大因数也是6,此时倍数和因数相等。因此,倍数不一定比因数大,原说法错误。
故答案为:×
16.B
【分析】除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。据此确定质数、合数、奇数和偶数的个数,比较,哪种数的个数最少,抽到哪种数的可能性就最小。
【详解】质数有2,3,5,7,共4个;合数有4,6,共2个;奇数有1、3、5、7,共4个;偶数有2,4,6,共3个,2<3<4,最少的是合数,抽到合数的可能性最小。
故答案为:B
17.C
【分析】根据2的倍数的特征,一个数的个位如果是偶数,这个数就是2的倍数;根据5的倍数的特征,一个数的个位是0或5,这个数就是5的倍数;个位上必需是0,才能满足既是2的倍数又是5的倍数,现在四位数变成15□0;然后再判断是不是3的倍数即可,3的倍数的特征是;各个数位上的和是3的倍数这个数就是3的倍数,把15□0中1、5、0加起来,即1+5+0=6,6是3的倍数,则分析6再加上10以内的几是3的倍数,□里就填几,然后数出填法有几种即可。
【详解】6+0=6
6+3=9
6+6=12
6+9=15
在□中可填0、3、6、9共4种填法。
故答案为:C
18.D
【分析】已知a、b均为自然数,且a÷2=b,则a=2b,我们就说a是2和b的倍数,2和b是a的因数。根据是2的倍数的数叫做偶数,即a是偶数。b是否是2的倍数,可举例说明,据此解答。
【详解】因为a÷2=b
所以a=2b
A.a是b的倍数,该说法正确。
B.a是偶数,该说法正确。
C.b是a的因数,该说法正确。
D.由 a÷2=b,若 ,则 ,此时b不是2的倍数。因此b不一定是2的倍数。该说法错误。
故答案为:D
19.A
【分析】除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数。据此确定和是11的质数与合数的所有情况,再分别求积即可。
【详解】11=2+9=3+8=5+6=7+4
2×9=18;3×8=24;5×6=30;7×4=28
一个质数与一个合数的和是11,它们的积可能是18、24、30、28,不可能是10。
故答案为:A
20.C
【分析】个位上是0,2,4,6,8的数是2的倍数;如果一个数的各个数位上的数的和是3的倍数,那么这个数就是3的倍数,根据题目条件逐步分析得出这 100个数的特征,进而判断平均数的特点;
除以2的余数情况:因为任意两个数的和是2的倍数,两个数相加和是2的倍数,说明这两个数要么都是偶数(即除以2余数为0),要么都是奇数(即除以2余数为1)。又因为这100个数互相不成倍数,所以不能都是偶数(如果都是偶数,必然存在倍数关系),所以这100个数除以2的余数都为1。
除以3的余数情况:由于任意三个数的和是3的倍数,设这三个数分别为a、b、c,a+b+c=3k(k为整数)。根据余数的性质,a、b、c除以3的余数之和要是3的倍数。因为这100个数互相不成倍数,若有不同余数,就很难保证任意三个数和是3的倍数,所以这100个数除以3的余数都相同,又因为要满足和是3的倍数,所以余数只能为1(若余数为0,则这些数有倍数关系)。
除以4的余数情况:同理,任意四个数的和是4的倍数,设这四个数为m、n、p、q,m+n+p+q=4s(s为整数),根据余数性质,这100个数除以4的余数之和要是4的倍数。由于这100个数互相不成倍数,所以它们除以4的余数都相同,且为1(若余数为0或其他情况容易出现倍数关系不符合题意)。
除以6的余数情况:任意六个数的和是6的倍数,设这六个数为、、、、、,+++++=6t(t为整数),根据余数性质,这100个数除以6的余数之和要是6的倍数。因为这100个数互相不成倍数,所以它们除以6的余数都相同,且为1(若余数为0或其他情况,会出现倍数关系不符合要求)。
分析平均数:因为这100个数的平均数等于这100个数的总和除以100,而这100个数除以2、3、4、6余数都为1,那么它们的平均数除以2、3、4、6余数也都为1。
【详解】A.505÷2=252……1,505÷3=168……1,505÷4=126……1,505÷6=84……1,满足余数都为1;
B.600÷2=300,余数为0,不满足除以2余数为1,所以B选项错误;
C.601÷2=300……1,601÷3=200……1、601÷4=150……1、601÷6=100……1,满足余数都为1;
D.606÷2=303,余数为0,不满足除以2余数为1,所以D选项错误。
比较505和601,505<601,但题目问的是这101个数平均数的最小值,因为101个数中有100个数满足上述余数条件,当这100个数最小且满足余数条件时,平均数会最小,601比505更符合这101个数平均数最小的情况(因为505作为平均数时,可能无法满足101个数整体的条件,而601满足所有余数条件且能保证101个数整体的合理性)。
故答案为:C
【点睛】找出这100个数余数的特点,通过余数特点来判断平均数满足的条件是解题的关键。
21.见详解
【分析】4的倍数是指能被4整除的数,也就是说,这个数除以4的余数是0。可以通过用除法计算得解。
30能整除的数,就是30的因数,也就是说,30除以这个数的余数是0,可以通过用除法计算得解。
9的倍数是指能被4整除的数,也就是说,这个数除以9的余数是0。可以通过用除法计算得解。据此解答。
【详解】60÷4=15
12÷4=3
20÷4=5
8÷4=2
48÷4=12
72÷4=18
4÷4=1
30÷2=15
30÷5=6
30÷3=10
27÷9=3
72÷9=8
54÷9=6
连线如下:
22.见详解
【分析】根据奇偶数的运算性质:奇数±奇数=偶数;偶数±偶数=偶数;奇数±偶数=奇数;解答即可。
【详解】由分析可得:361是奇数,放进两个棋和就是将361分成两部分,即分成两个数。
如果一个数是偶数,那么另一个数一定是奇数;
如果一个数是奇数,那么另一个数一定是偶数。
答:如果甲盒装的棋子数为偶数,那么乙盒装的棋子数是奇数,如果甲盒装的棋子数为奇数那么乙盒装的棋子数是偶数。
23.是;是;举例见详解
【分析】5的倍数特征:个位上的数字是0或5的数是5的倍数。
2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。
【详解】一个数个位上是0或5,这个数就是5的倍数,如10、15、20、25、135……
一个数个位上是0、2、4、6或8,这个数就是2的倍数,如12、14、16、18、100……
24.不对
【分析】马蹄莲10元/枝,郁金香5元/枝,妈妈在花店买了一些马蹄莲和郁金香,则马蹄莲总钱数为10的倍数,郁金香总钱数是5的倍数。又由10=5×2,则马蹄莲总钱数为5的倍数,马蹄莲和郁金香总钱数是5的倍数;据此解答。
【详解】由分析可知:马蹄莲和郁金香的总钱数是5的倍数,而87的个位上是7,所以87不是5的倍数,所以店员说的不对。
25.见详解
【分析】个位上是0或5的数,是5的倍数;各位上数的和是3的倍数的数,是3的倍数,据此解题。
【详解】7+8=15
答:如果每5颗分给一个小朋友,不能正好分完,因为78的个位上是8,不符合5的倍数的特征。
如果每3颗分给一个小朋友,能正好分完,因为15是3的倍数,那么78也是3的倍数。
26.247平方厘米
【分析】根据长方体的周长=(长+宽)×2,用64÷2即可求出一条长和一条宽的和,也就是32厘米,一个数只有1和它本身两个因数,这个数叫做质数。32=3+29=13+19,所以长方形有2种情况,根据长方形的面积=长×宽,分别求出两种情况的面积,再比较即可。
【详解】64÷2=32(厘米)
32=3+29=13+19
3×29=87(平方厘米)
13×19=247(平方厘米)
87<247
答:这个长方形的面积最多可以是247平方厘米。
27.7种
【分析】找一个数的因数,可以利用乘法算式,按因数从小到大的顺序一组一组地找,这时,两个乘数都是积的因数。求出36有多少个因数,进而找出符合条件的排法即可。
【详解】36=1×36,排成1行或者36行,都不符合题意;
36=2×18,排成2行或者18行;
36=3×12,排成3行或者排成12行;
36=4×9,排成4行或者排成9行;
36=6×6,排成6行。
答:一共有7种不同的排法。
28.36人
【分析】根据题意,五(1)班的人数同时是3、4、6的倍数,用列举法找出3、4、6的倍数,并且保证人数在30~40之间,据此解答。
【详解】3的倍数:3、6、9、12、15、18、21、24、27、30、33、36、39…
4的倍数:4、8、12、16、20、24、28、32、36、40…
6的倍数:6、12、18、24、30、36、42…
所以36同时是3、4、6的倍数,且在30~40之间。
答:五(1)班有36人。
29.372
【分析】既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。除了1和它本身以外不再有其他因数,这样的数叫质数。
【详解】能同时是2和3的倍数,个位上的数字是0、2、4、6、8,质数有2;
10以内的质数有:2、3、5、7,2如果在个位,百位和十位能选择的数是3和7。
答:这个三位数可能是372或732。
30.能确定是偶数
【分析】根据题意,可以设每人答对a道,答错b道,则不答的题有(50-a-b)道;那么答对的题的得分是3a分,不答的题的得分是1×(50-a-b)分,答错的题的得分是(1×b)分,再相加,即是每人的总得分;然后分析这个总分数是奇数还是偶数,设这部分学生人数是偶数或奇数,根据奇数与偶数的运算性质确定这部分学生得分的总和能否确定是偶数还是奇数。
奇数和偶数的运算性质:
偶数+偶数=偶数,奇数+奇数=偶数,奇数+偶数=奇数;
奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数。
【详解】设每人答对a道,答错b道,则不答的题有(50-a-b)道,那么每人的得分是:
3×a+1×(50-a-b)-1×b
=3a+50-a-b-b
=(2a-2b+50)(分)
无论a、b是奇数还是偶数,2a、2b都是偶数,50也是偶数,偶数-偶数=偶数,偶数+偶数=偶数,所以(2a-2b+50)是偶数,即每人的得分是偶数。
如果这部分学生人数是偶数,则偶数×偶数=偶数;
如果这部分学生人数是奇数,则偶数×奇数=偶数。
答:这部分学生得分的总和能确定是偶数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
