2024-2025学年安徽省皖北县中联盟高二下学期3月联考数学试题(B卷)(含答案)
文档属性
| 名称 | 2024-2025学年安徽省皖北县中联盟高二下学期3月联考数学试题(B卷)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 10:29:03 | ||
图片预览



文档简介
2024-2025学年安徽省皖北县中联盟高二下学期3月联考数学试题(B卷)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知函数f(x)=x-1,则=( )
A. 1 B. 0 C. -1 D. -2
2.已知等差数列{}的前n项和为,若=1,则=( )
A. B. 10 C. 19 D. 38
3.下列求导的运算正确的是( )
A. (x-)'= B. (x)'=
C. ()'=(+) D. ((4x+1))'=
4.已知单调递减的等比数列{}满足=,+=,则=( )
A. B. C. 512 D. 1024
5.已知点P是抛物线C:=4x上任意一点,若点P到抛物线C的准线的距离为,到直线m:2x-y+3=0的距离为,则+的最小值是( )
A. 1+ B. C. D.
6.在平面直角坐标系中,A(0,3),B(0,-1),点P满足|PA|=2|PB|,则PAB面积的最大值是( )
A. 2 B. C. D.
7.已知定义域为R的函数f(x)满足f(1)=,且f(x)+f'(x)<0,则不等式f(x+1)>的解集是( )
A. (2,+) B. (-,2) C. (0,+) D. (-,0)
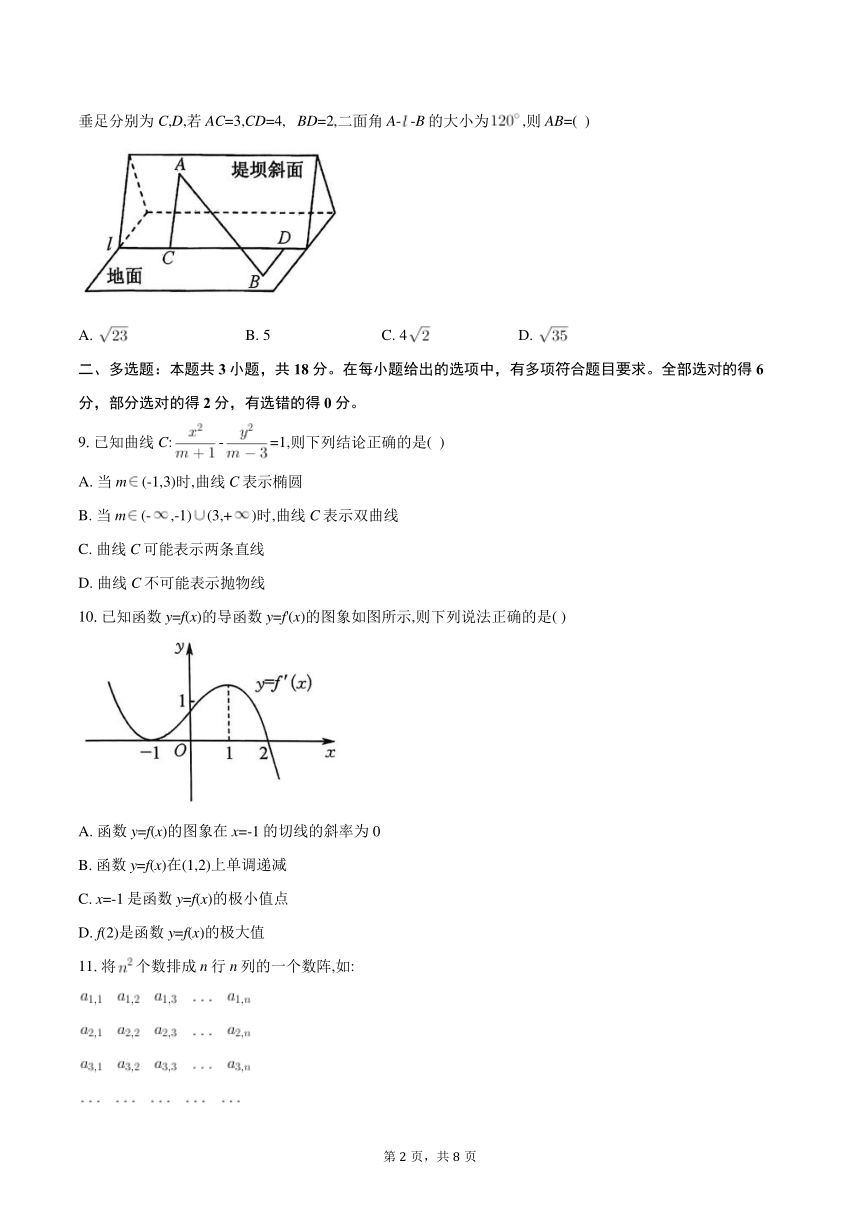
8.郑国渠是秦王嬴政命郑国修建的著名水利工程,先人用智慧和勤劳修筑了一道道坚固的堤坝.如图是一道堤坝的示意图,堤坝斜面与底面的交线记为,点A,B分别在堤坝斜面与地面上,过点A,B分别作直线的垂线,垂足分别为C,D,若AC=3,CD=4, BD=2,二面角A- -B的大小为,则AB=( )
A. B. 5 C. 4 D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知曲线C:-=1,则下列结论正确的是( )
A. 当m(-1,3)时,曲线C表示椭圆
B. 当m(-,-1)(3,+)时,曲线C表示双曲线
C. 曲线C可能表示两条直线
D. 曲线C不可能表示抛物线
10.已知函数y=f(x)的导函数y=f'(x)的图象如图所示,则下列说法正确的是( )
A. 函数y=f(x)的图象在x=-1的切线的斜率为0
B. 函数y=f(x)在(1,2)上单调递减
C. x=-1是函数y=f(x)的极小值点
D. f(2)是函数y=f(x)的极大值
11.将个数排成n行n列的一个数阵,如:
该数阵第一列的 n个数从上到下构成以d为公差的等差数列,每一行的n个数从左到右构成以d为公比的等比数列(其中d>0).已知=1,=+1,记这个数的和为S,则下列说法正确的有( )
A. d=2 B. =512
C. =(2i-1) D. S=(-1)
三、填空题:本题共3小题,每小题5分,共15分。
12.函数f(x)=2x+的图象在x=1处的切线方程是 .
13.已知数列{ }的前n项和为,若(2n-1)=(2n+1)(n),=1,则= .
14.已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为,,过点的直线 与双曲线C的右支和左支分别交于点A,B,若的面积为,且的面积是面积的2倍,则双曲线C的离心率为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知:+-2x-4y+4=0与:++6x+2y+a=0只有一条公切线,且公切点为M,点P是上异于点M的一点,过点P作的另一条切线,切点为N.
(1)求a的值及直线的方程;
(2)若PMN是等腰直角三角形,求直线PN的方程.
16.(本小题12分)
已知数列{}满足=,=2.
(1)求证:数列{+}是等比数列,并求数列{}的通项公式;
(2)求数列{}的前n项和.
17.(本小题12分)
已知函数f(x)=-(a+1)x+ax(a>0).
(1)讨论函数f(x)的单调性;
(2)若a>,求证:对,(0,+)且,都有+a>0.
18.(本小题12分)
已知椭圆C的中心为坐标原点,对称轴为x轴与y轴,且C经过点(1,),(,).
(1)求C的标准方程;
(2)若F是C的右焦点,过F作两条互相垂直的直线,,直线与C交于A,B两点,直线与C交于D,E两点.求四边形ADBE面积的取值范围.
19.(本小题12分)
在平面直角坐标系O-xy中,任何一条直线都可以用ax+by+c=0(其中a,b,cR,+0)表示,给定一个点和一个方向,我们可以确定一条直线,例如:已知点P(2,3)在直线上,=(2,1)是直线的一个方向向量,则直线上任意一点Q(x,y)满足,化简得直线的方程为x-2y+4=0.而在空间直角坐标系O-xyz中,任何一个平面的方程都可以表示成ax+by+cz+d=0(其中a,b,c,dR,且++0),类似的,在空间中,给定一个点和一个平面的法向量也可以确定一个平面.
(1)若点F(1,0,0),G(2,1,1),H(0,2,0),求平面FGH的方程;
(2)求证:=(a,b,c)是平面ax+by+cz+d=0(++0)的一个法向量;
(3)已知某平行六面体ABCD-,平面的方程为2x-y+2z+1=0,平面经过点R(0,1,2),S(1,1,3),T(2,2,4),平面的方程为kx-3y+2kz-3=0,求平面与平面夹角的余弦值.
答案
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】BD
10.【答案】AD
11.【答案】ACD
12.【答案】6x-2y-5=0
13.【答案】2500
14.【答案】
15.【答案】解:(1)可化为+=1,圆心(1,2),半径=1,
可化为+=10-a,圆心(-3,-1),半径=.
因为与只有一条公切线,
所以两圆内切,|=-|,即5=|-1|,
解得a=-26.
两圆相减,得公切线l的方程为8x+6y-30=0,即4x+3y-15=0.
(2)由题意,得|PM|=|PN|,
若PMN是等腰直角三角形,
所以MPN=,故=-1,
由(1)可知直线PM的斜率=-,所以直线PN的斜率=.
设直线PN的方程为3x-4y+=0,
所以点到直线PN的距离d==1,解得=0或=10,
所以直线PN的方程为3x-4y=0或3x-4y+10=0.
16.【答案】解:(1)证明:因为=2,=,
所以0,==+,
所以+=2(+).
因为+=10,所以=2,
所以数列{+}是以1为首项,2为公比的等比数列,
所以+=,即==.
(2)解:因为=n-,
所以=1+2+3++n-(++++).
其中++++=
令=1+2+3++n,
=1+2+3++n,
两式相减,得-=1+2+++-n=-n=(1-n)-1.
所以=(n-1)+1,
所以=(n-1)-+1.
17.【答案】解:(1)f(x)的定义域为(0,+∞).
所以f'(x)=x-(a+1)+==,
当0< a<1时,令f'(x)>0,得0< x< a或x>1,
令f'(x)<0,得a< x<1,所以函数f(x)在(0,a)上单调递增,在(a,1)上单调递减,在(1,+)上单调递增,
当a=1时,f'(x)=0恒成立,所以函数f(x)在(0,+)上单调递增;
当a>1时,令f'(x)>0,得0< x<1或x>a,令f'(x)<0,得1< x< a,
所以函数f(x) 在(0, 1) 上单调递增, 在(1,a) 上单调递减,在(a,+)上单调递增;
(2)证明:不妨设<,要证对,(0,+),都有+a>0,
只需证f()-f()<-a(-),即需证f()+< f()+,
构造函数g(x)=f(x)+ax=-x+ax,则需证函数g(x)在(0,+)上为增函数,
因为g'(x)=x-1+2-1>2-1=0,
所以函数g(x)在(0,+)上为增函数成立,
所以当a>时,对,(0,+)且,都有+a>0.
18.【答案】解:(1)设C的方程为+=1,
将点(1,),(,)代入,
得,解得,
所以C的标准方程为+=1.
(2)当直线的斜率为0,直线的斜率不存在时,|AB|=2a=2,|DE|==,
当直线的斜率不存在,直线的斜率为0时,|AB|=,|DE|=2,
所以四边形ADBE的面积S=|AB||DE|=2=2.
当直线,的斜率存在且不为0时,
设直线的方程为y=k(x-1),A(,),B(,),
联立,得(1+)-x+-2=0,
由题意得>0,+=,=.
所以|AB|=-|
==,
同理|DE|=,
四边形ADBE的面积S=|AB||DE|
=
=,
令t=+1(t>1),
则S===(0<<1),
所以当=,即k=1时,=,所以S<2.
综上所述,四边形ADBE面积的取值范围[,2].
19.【答案】(1)解:=(1,1,1),=(-1,2,0),设=(,,)是平面FGH的一个法向量,
则令=2,得=1,=-3,所以=(2,1,-3).
设点I(x,y,z)是平面FGH内任意一点,由,得=2(x-1)+y-3z=0,
所以平面FGH的方程为2x+y-3z-2=0.
(2)证明:记平面的方程为ax+by+cz+d=0,在平面上任取一条直线,直线上任取两点M(,,),N(,,),
则有,因为=(-,-,-),=(a,b,c),
所以=a(-)+b(-)+c(-)=(++)-(++)=-d-(-d)=0.
所以,即垂直于平面上任意一条直线,所以=(a,b,c)是平面ax+by+cz+d=0的一个法向量.
(3)解:=(1,0,1)=(2,1,2),设=(i,j,r)为平面的一个法向量,
则令i=1,得j=0,r=-1,所以=(1,0,-1).
因为平面的方程为2x-y+2z+1=0,所以由(2)知平面的一个法向量为=(2,-1,2),
设直线的一个方向向量为=(,,),则
令=1,得=4,=1,所以=(1,4,1).
因为平面,所以平面的一个法向量=(k,-3,2k)与直线的方向向量=(1,4,1)垂直,
所以=k-12+2k=0,解得k=4,所以=(4,-3,8)
所以平面与平面夹角的余弦值为==.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知函数f(x)=x-1,则=( )
A. 1 B. 0 C. -1 D. -2
2.已知等差数列{}的前n项和为,若=1,则=( )
A. B. 10 C. 19 D. 38
3.下列求导的运算正确的是( )
A. (x-)'= B. (x)'=
C. ()'=(+) D. ((4x+1))'=
4.已知单调递减的等比数列{}满足=,+=,则=( )
A. B. C. 512 D. 1024
5.已知点P是抛物线C:=4x上任意一点,若点P到抛物线C的准线的距离为,到直线m:2x-y+3=0的距离为,则+的最小值是( )
A. 1+ B. C. D.
6.在平面直角坐标系中,A(0,3),B(0,-1),点P满足|PA|=2|PB|,则PAB面积的最大值是( )
A. 2 B. C. D.
7.已知定义域为R的函数f(x)满足f(1)=,且f(x)+f'(x)<0,则不等式f(x+1)>的解集是( )
A. (2,+) B. (-,2) C. (0,+) D. (-,0)
8.郑国渠是秦王嬴政命郑国修建的著名水利工程,先人用智慧和勤劳修筑了一道道坚固的堤坝.如图是一道堤坝的示意图,堤坝斜面与底面的交线记为,点A,B分别在堤坝斜面与地面上,过点A,B分别作直线的垂线,垂足分别为C,D,若AC=3,CD=4, BD=2,二面角A- -B的大小为,则AB=( )
A. B. 5 C. 4 D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知曲线C:-=1,则下列结论正确的是( )
A. 当m(-1,3)时,曲线C表示椭圆
B. 当m(-,-1)(3,+)时,曲线C表示双曲线
C. 曲线C可能表示两条直线
D. 曲线C不可能表示抛物线
10.已知函数y=f(x)的导函数y=f'(x)的图象如图所示,则下列说法正确的是( )
A. 函数y=f(x)的图象在x=-1的切线的斜率为0
B. 函数y=f(x)在(1,2)上单调递减
C. x=-1是函数y=f(x)的极小值点
D. f(2)是函数y=f(x)的极大值
11.将个数排成n行n列的一个数阵,如:
该数阵第一列的 n个数从上到下构成以d为公差的等差数列,每一行的n个数从左到右构成以d为公比的等比数列(其中d>0).已知=1,=+1,记这个数的和为S,则下列说法正确的有( )
A. d=2 B. =512
C. =(2i-1) D. S=(-1)
三、填空题:本题共3小题,每小题5分,共15分。
12.函数f(x)=2x+的图象在x=1处的切线方程是 .
13.已知数列{ }的前n项和为,若(2n-1)=(2n+1)(n),=1,则= .
14.已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为,,过点的直线 与双曲线C的右支和左支分别交于点A,B,若的面积为,且的面积是面积的2倍,则双曲线C的离心率为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
已知:+-2x-4y+4=0与:++6x+2y+a=0只有一条公切线,且公切点为M,点P是上异于点M的一点,过点P作的另一条切线,切点为N.
(1)求a的值及直线的方程;
(2)若PMN是等腰直角三角形,求直线PN的方程.
16.(本小题12分)
已知数列{}满足=,=2.
(1)求证:数列{+}是等比数列,并求数列{}的通项公式;
(2)求数列{}的前n项和.
17.(本小题12分)
已知函数f(x)=-(a+1)x+ax(a>0).
(1)讨论函数f(x)的单调性;
(2)若a>,求证:对,(0,+)且,都有+a>0.
18.(本小题12分)
已知椭圆C的中心为坐标原点,对称轴为x轴与y轴,且C经过点(1,),(,).
(1)求C的标准方程;
(2)若F是C的右焦点,过F作两条互相垂直的直线,,直线与C交于A,B两点,直线与C交于D,E两点.求四边形ADBE面积的取值范围.
19.(本小题12分)
在平面直角坐标系O-xy中,任何一条直线都可以用ax+by+c=0(其中a,b,cR,+0)表示,给定一个点和一个方向,我们可以确定一条直线,例如:已知点P(2,3)在直线上,=(2,1)是直线的一个方向向量,则直线上任意一点Q(x,y)满足,化简得直线的方程为x-2y+4=0.而在空间直角坐标系O-xyz中,任何一个平面的方程都可以表示成ax+by+cz+d=0(其中a,b,c,dR,且++0),类似的,在空间中,给定一个点和一个平面的法向量也可以确定一个平面.
(1)若点F(1,0,0),G(2,1,1),H(0,2,0),求平面FGH的方程;
(2)求证:=(a,b,c)是平面ax+by+cz+d=0(++0)的一个法向量;
(3)已知某平行六面体ABCD-,平面的方程为2x-y+2z+1=0,平面经过点R(0,1,2),S(1,1,3),T(2,2,4),平面的方程为kx-3y+2kz-3=0,求平面与平面夹角的余弦值.
答案
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】BD
10.【答案】AD
11.【答案】ACD
12.【答案】6x-2y-5=0
13.【答案】2500
14.【答案】
15.【答案】解:(1)可化为+=1,圆心(1,2),半径=1,
可化为+=10-a,圆心(-3,-1),半径=.
因为与只有一条公切线,
所以两圆内切,|=-|,即5=|-1|,
解得a=-26.
两圆相减,得公切线l的方程为8x+6y-30=0,即4x+3y-15=0.
(2)由题意,得|PM|=|PN|,
若PMN是等腰直角三角形,
所以MPN=,故=-1,
由(1)可知直线PM的斜率=-,所以直线PN的斜率=.
设直线PN的方程为3x-4y+=0,
所以点到直线PN的距离d==1,解得=0或=10,
所以直线PN的方程为3x-4y=0或3x-4y+10=0.
16.【答案】解:(1)证明:因为=2,=,
所以0,==+,
所以+=2(+).
因为+=10,所以=2,
所以数列{+}是以1为首项,2为公比的等比数列,
所以+=,即==.
(2)解:因为=n-,
所以=1+2+3++n-(++++).
其中++++=
令=1+2+3++n,
=1+2+3++n,
两式相减,得-=1+2+++-n=-n=(1-n)-1.
所以=(n-1)+1,
所以=(n-1)-+1.
17.【答案】解:(1)f(x)的定义域为(0,+∞).
所以f'(x)=x-(a+1)+==,
当0< a<1时,令f'(x)>0,得0< x< a或x>1,
令f'(x)<0,得a< x<1,所以函数f(x)在(0,a)上单调递增,在(a,1)上单调递减,在(1,+)上单调递增,
当a=1时,f'(x)=0恒成立,所以函数f(x)在(0,+)上单调递增;
当a>1时,令f'(x)>0,得0< x<1或x>a,令f'(x)<0,得1< x< a,
所以函数f(x) 在(0, 1) 上单调递增, 在(1,a) 上单调递减,在(a,+)上单调递增;
(2)证明:不妨设<,要证对,(0,+),都有+a>0,
只需证f()-f()<-a(-),即需证f()+< f()+,
构造函数g(x)=f(x)+ax=-x+ax,则需证函数g(x)在(0,+)上为增函数,
因为g'(x)=x-1+2-1>2-1=0,
所以函数g(x)在(0,+)上为增函数成立,
所以当a>时,对,(0,+)且,都有+a>0.
18.【答案】解:(1)设C的方程为+=1,
将点(1,),(,)代入,
得,解得,
所以C的标准方程为+=1.
(2)当直线的斜率为0,直线的斜率不存在时,|AB|=2a=2,|DE|==,
当直线的斜率不存在,直线的斜率为0时,|AB|=,|DE|=2,
所以四边形ADBE的面积S=|AB||DE|=2=2.
当直线,的斜率存在且不为0时,
设直线的方程为y=k(x-1),A(,),B(,),
联立,得(1+)-x+-2=0,
由题意得>0,+=,=.
所以|AB|=-|
==,
同理|DE|=,
四边形ADBE的面积S=|AB||DE|
=
=,
令t=+1(t>1),
则S===(0<<1),
所以当=,即k=1时,=,所以S<2.
综上所述,四边形ADBE面积的取值范围[,2].
19.【答案】(1)解:=(1,1,1),=(-1,2,0),设=(,,)是平面FGH的一个法向量,
则令=2,得=1,=-3,所以=(2,1,-3).
设点I(x,y,z)是平面FGH内任意一点,由,得=2(x-1)+y-3z=0,
所以平面FGH的方程为2x+y-3z-2=0.
(2)证明:记平面的方程为ax+by+cz+d=0,在平面上任取一条直线,直线上任取两点M(,,),N(,,),
则有,因为=(-,-,-),=(a,b,c),
所以=a(-)+b(-)+c(-)=(++)-(++)=-d-(-d)=0.
所以,即垂直于平面上任意一条直线,所以=(a,b,c)是平面ax+by+cz+d=0的一个法向量.
(3)解:=(1,0,1)=(2,1,2),设=(i,j,r)为平面的一个法向量,
则令i=1,得j=0,r=-1,所以=(1,0,-1).
因为平面的方程为2x-y+2z+1=0,所以由(2)知平面的一个法向量为=(2,-1,2),
设直线的一个方向向量为=(,,),则
令=1,得=4,=1,所以=(1,4,1).
因为平面,所以平面的一个法向量=(k,-3,2k)与直线的方向向量=(1,4,1)垂直,
所以=k-12+2k=0,解得k=4,所以=(4,-3,8)
所以平面与平面夹角的余弦值为==.
第1页,共1页
同课章节目录
