期中考试真题分类汇编11 填空题(含答案+解析)---2024-2025学年苏教版六年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编11 填空题(含答案+解析)---2024-2025学年苏教版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 240.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 07:44:12 | ||
图片预览



文档简介
2024-2025学年苏教版六年级数学下册
期中考试真题分类汇编11 填空题
一、填空题
1.(2024六下·江门期中)把2米长的圆柱形木棒锯成三段,表面积增加了40dm3,原来木棒的体积是 dm3
2.(2024六下·鹰潭期中)如果a与b互为倒数,并且那么c= ,= 。
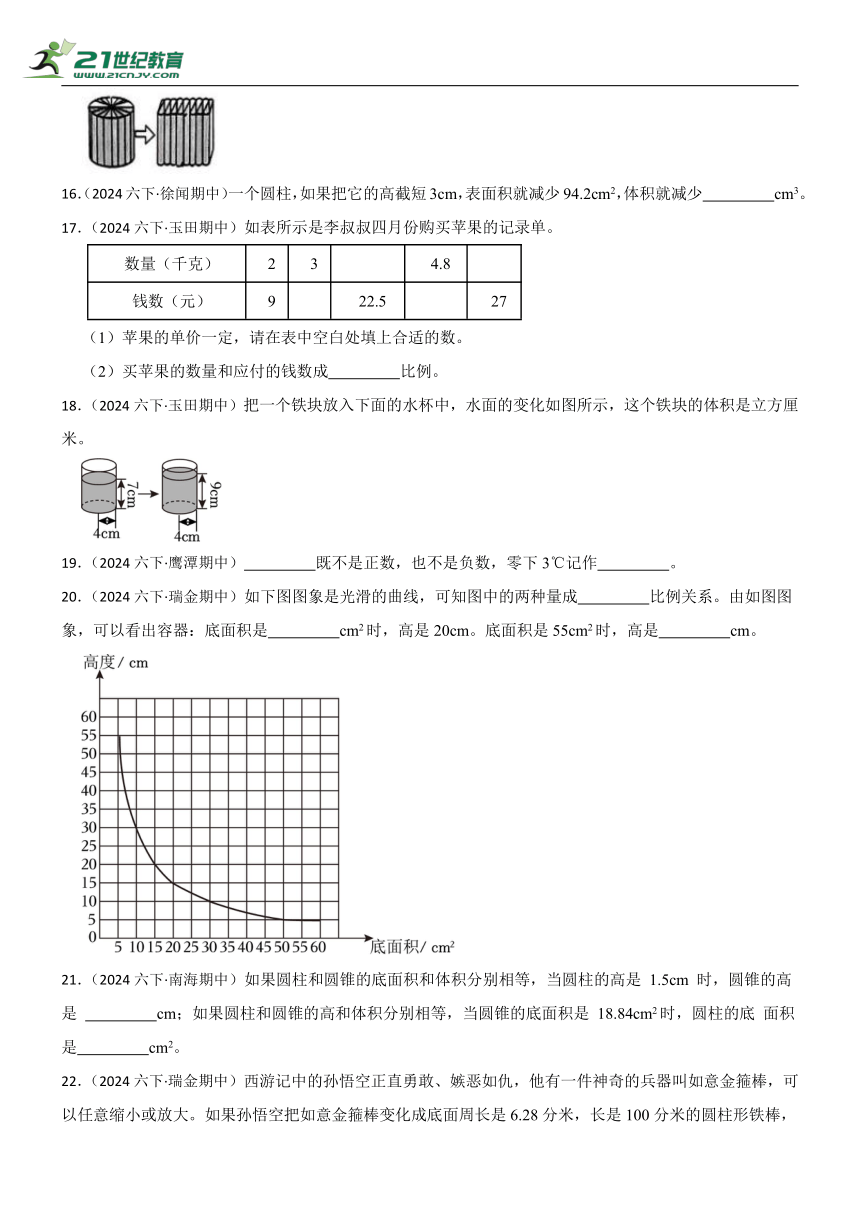
3.(2024六下·玉田期中)实验小学六⑴班学生的平均体重是39千克,如表所示是该班5名学生的体重统计表
学号 1 2 3 4 5
体重(千克) 35 39 50
与平均体重相比(千克) ﹣4 +5 ﹣7
4.(2024六下·江门期中)在一幅比例尺是1:20000000的地图上,量得甲乙两地的距离为3.04 厘米,那么这两地的实际距离是 千米:如果汽车每小时行驶 80千米,从甲地到乙地要 小时。
5.(2024六下·大余期中)用一张长15cm,宽12cm的长方形纸围成一个圆柱,圆柱的侧面积是 cm2。
6.(2024六下·江门期中)甲数的等于乙数的 (甲、乙均不为0),甲数与乙数的比是 。
7.(2024六下·江门期中)用18的因数写出一个比例是 。
8.(2024六下·鹰潭期中)写出两个比值都是的比,再组成比例是 。
9.(2024六下·江门期中)3÷5= :20= = (填小数)= %= 成。
10.(2024六下·江门期中)一件衣服打八五折出售,也就是便宜 %,便宜了30元,衣服原价是 元。
11.(2024六下·江门期中)一个圆柱的底面直径是4cm,高是15cm,它的侧面积是 cm2,表面积是 cm2,体积是 cm3.
12.(2024六下·江门期中)一个正方体木块的棱长是6cm,把它削成一个最大的圆柱体。圆柱体的体积是 cm3。再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积是 cm3。
13.(2024六下·瑞金期中)某市2023年接待旅游总人数约为96万人次,比上一年增长约16万人次。该市2023年接待旅游总人数比2022年增长 成。
14.(2024六下·鹰潭期中)一个圆柱的底面直径和高都是10cm,这个圆柱的侧面积是 。
15.(2024六下·南海期中)如图把圆柱沿高切成若干偶数等份,拼起来就是一个近似的长方体。这个长方体的高为 5cm,它的表面积比圆柱多 40cm2。圆柱的体积是 cm3,表面 积是 cm2。
16.(2024六下·徐闻期中)一个圆柱,如果把它的高截短3cm,表面积就减少94.2cm2,体积就减少 cm3。
17.(2024六下·玉田期中)如表所示是李叔叔四月份购买苹果的记录单。
数量(千克) 2 3 4.8
钱数(元) 9 22.5 27
(1)苹果的单价一定,请在表中空白处填上合适的数。
(2)买苹果的数量和应付的钱数成 比例。
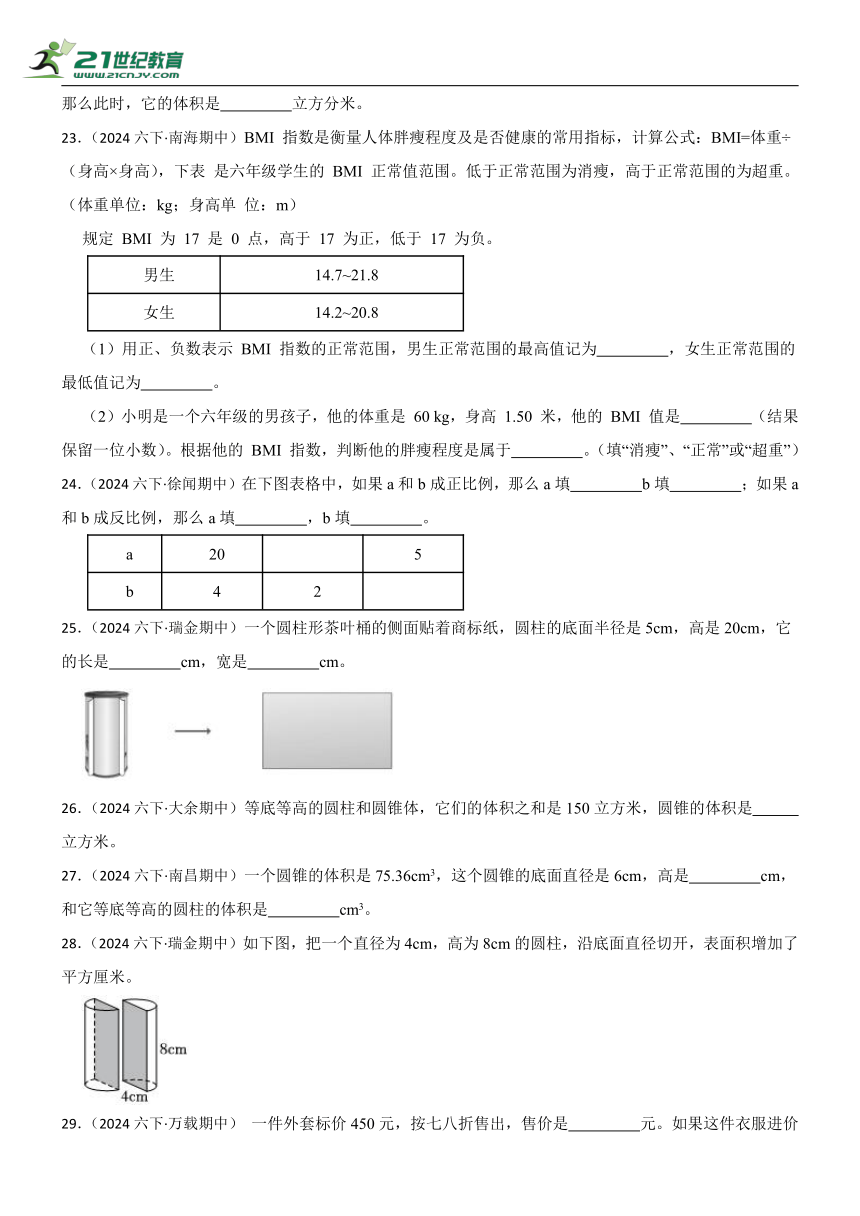
18.(2024六下·玉田期中)把一个铁块放入下面的水杯中,水面的变化如图所示,这个铁块的体积是立方厘米。
19.(2024六下·鹰潭期中) 既不是正数,也不是负数,零下3℃记作 。
20.(2024六下·瑞金期中)如下图图象是光滑的曲线,可知图中的两种量成 比例关系。由如图图象,可以看出容器:底面积是 cm2时,高是20cm。底面积是55cm2时,高是 cm。
21.(2024六下·南海期中)如果圆柱和圆锥的底面积和体积分别相等,当圆柱的高是 1.5cm 时,圆锥的高是 cm;如果圆柱和圆锥的高和体积分别相等,当圆锥的底面积是 18.84cm2时,圆柱的底 面积是 cm2。
22.(2024六下·瑞金期中)西游记中的孙悟空正直勇敢、嫉恶如仇,他有一件神奇的兵器叫如意金箍棒,可以任意缩小或放大。如果孙悟空把如意金箍棒变化成底面周长是6.28分米,长是100分米的圆柱形铁棒,那么此时,它的体积是 立方分米。
23.(2024六下·南海期中)BMI 指数是衡量人体胖瘦程度及是否健康的常用指标,计算公式:BMI=体重÷(身高×身高),下表 是六年级学生的 BMI 正常值范围。低于正常范围为消瘦,高于正常范围的为超重。(体重单位:kg;身高单 位:m)
规定 BMI 为 17 是 0 点,高于 17 为正,低于 17 为负。
男生 14.7~21.8
女生 14.2~20.8
(1)用正、负数表示 BMI 指数的正常范围,男生正常范围的最高值记为 ,女生正常范围的最低值记为 。
(2)小明是一个六年级的男孩子,他的体重是 60 kg,身高 1.50 米,他的 BMI 值是 (结果保留一位小数)。根据他的 BMI 指数,判断他的胖瘦程度是属于 。(填“消瘦”、“正常”或“超重”)
24.(2024六下·徐闻期中)在下图表格中,如果a和b成正比例,那么a填 b填 ;如果a和b成反比例,那么a填 ,b填 。
a 20 5
b 4 2
25.(2024六下·瑞金期中)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,它的长是 cm,宽是 cm。
26.(2024六下·大余期中)等底等高的圆柱和圆锥体,它们的体积之和是150立方米,圆锥的体积是 立方米。
27.(2024六下·南昌期中)一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是 cm,和它等底等高的圆柱的体积是 cm3。
28.(2024六下·瑞金期中)如下图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了 平方厘米。
29.(2024六下·万载期中) 一件外套标价450元,按七八折售出,售价是 元。如果这件衣服进价是300元,售出这件衣服的利润是 元,利润率是 。
30.(2024六下·玉田期中)当=(y≠0)时,x和y成 比例。
31.(2024六下·玉田期中)把一个底面直径是16厘米,长是15厘米的圆柱形木头沿着底面直径竖直锯开后,表面积比原来增加 平方厘米。
32.(2024六下·南海期中)某新建商品房开售,每平方米 9000 元,阳阳的爸爸购买了一 套 100m2的房子,需要缴纳一定的契税(缴纳标准如图)。购买这套房子 一共需要缴纳 元的契税。
契税 新建商品房按房屋总价 的 1.5%征收,购买 90m2及以 下的普通住房,契税按1%征收。
33.(2024六下·陆川期中)在一个比例里,两个内项互为倒数,其中一个外项是3,另一个外项是 .
34.(2024六下·鹰潭期中)把一个棱长是6cm的正方体削成一个最大的圆锥体,这个圆锥的体积是 。
35.(2024六下·南华期中)一幅地图的比例尺是1:2000000,它表示地图上的1cm代表实际的 m。若甲、乙两地相距600km,在这幅地图上应该画 cm。
36.(2024六下·瑞金期中) 一张精密仪器图纸,用5cm长表示实际长5mm,则这幅图的比例尺是 。
37.(2024六下·鹰潭期中)把3×40=20×6,改写成比例是 。
38.(2024六下·鹰潭期中)在中,图中1cm表示实际距离 km,改写成数值比例尺是 。
39.(2024六下·瑞金期中)妈妈把80000元存入银行,存期为三年定期,年利率1.95%。请提出数学问题: ,列出算式: 。
40.(2024六下·鹰潭期中)一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作 千米;+10千米表示 。
41.(2024六下·南华期中)若把六年级学生的平均体重50kg记作0kg,甲、乙、丙三名同学的体重被分别记为+4kg、-3kg、0kg,则他们三人的实际体重分别是 kg、 kg、 kg。
42.(2024六下·鹰潭期中)把一个圆柱侧面展开,得到一个正方形,这个圆柱的底面直径是8cm,圆柱的高是 。
43.(2024六下·大余期中)在比例尺为1:5000000的地图上,南昌、广州两地相距16cm,在另一幅比例尺为1:4000000的地图上,南昌、广州两地相距 厘米。
44.(2024六下·大余期中)一个直角三角形的两条直角边分别为6cm,10cm,若以6cm的边为轴旋转一周,所围图形的体积是 cm3。
45.(2024六下·大余期中)把一根长10dm的圆柱形钢柱截成两段,表面积比原来增加:,这根圆柱原来的体积是 dm3。
46.(2024六下·大余期中)天虹超市举行“五一”商品大推销,有一套“”玩具打九折出售,“九折”表示现价相当于原价的 %,如果这件玩具现价卖72元,那么原价是 。
47.(2024六下·大余期中)某地某日的气温是-4℃~4℃,这表明这天的最高气温是 ℃,最低气温是 ℃,温差是 。
48.(2024六下·南海期中)3D 电脑动画成像技术展示活动中,技术人员用一个直角三角形(如图),绕着一条直角 边旋转成一个 ,它的体积是 cm3。
49.(2024六下·南海期中)在一个比例中,两个内项的积是最小的质数,已知一个外项是,另一个外项是 。
50.(2024六下·徐闻期中)将一个棱长为3dm的正方体木块削成一个最大的圆锥体,这个圆锥体的体积为 dm3。
答案解析部分
1.200
解:2米=20分米
(3-1)×2=4(个)
40÷4=10(平方分米)
10×20=200(立方分米)
故答案为:200。
通过实际操作可知每锯一次就增加2个底面,因此根据题意可得:段数-1=锯的次数,(段数-1)×2=增加的底面个数,增加的表面积÷增加的底面个数=圆柱形木棒的底面积,圆柱形木棒的底面积×长=原木棒的体积;计算时统一单位:1米=10分米,大单位转化成小单位乘进率。
2.;
解:则ab=5c,ab=1,所以5c=1,则c=;
=×=。
故答案为:;。
根据比例的基本性质把这个比例写成两个內项积等于两个外项积的行驶,a与b互为倒数,则a、b的积是1,这样就能求出c的值,然后求出的值即可。
3.44;32;0;+11
解:第一空:39+5=44(千克)
第二空:39-7=32(千克)
第三空:39-39=0(千克)
第四空:50-39=11(千克)
学号 1 2 3 4 5
体重(千克) 35 44 39 50 32
与平均体重相比(千克) ﹣4 +5 0 +11 ﹣7
故答案为:44;32;0;+11。
比39千克多的质量用正数表示,比39千克少的质量用负数表示,正数表示比39千克多的质量,负数表示比39千克少的质量,据此解答。
4.608;7.6
解:3.04÷=60800000(厘米)
60800000厘米=608千米;
608÷80=7.6(小时)
故答案为:608;7.6。
根据题意可得:图上距离÷比例尺=实际距离,实际距离÷汽车的速度=需要的时间;在计算时统一单位:1千米=100000厘米,小单位转化成大单位除以进率。
5.180
解:15×12=180(平方厘米)
故答案为:180。
根据圆柱的侧面展开图的特点:圆柱的底面周长是长方形的长,圆柱的高是长方形的宽,所以这个圆柱的侧面积就是这个长方形的面积;用长乘宽即可。
6.5:18
解::
=(×30):(×30)
=5:18
故答案为:5:18。
因为,甲数×=乙数×,所以,根据比例的基本性质:两个外项的积等于两个内项的积,可得:甲数:乙数=:,再化简即可。
7.2:3=6:9
解:18的因数有1,2,3,6,9,18,即2×9=3×6,所以2:3=6:9。
故答案为:2:3=6:9。
求一个数的因数可以通过从1开始想哪两个数相乘等于这个数,那么这两个因数就都是这个数的因数;也可以通过用这个数从1开始除以一个数,找到没有余数的商和除数,就都是这个数的因数。1和它本身也是这个数的因数;
比例的基本性质:两个外项的积等于两个内项的积;
先根据因数找法找到18的因数,再找到乘积相等的算式,最后根据比例的基本性质即可写比例。
8.1:2=2:4
解:写出两个比值都是的比,再组成比例是1:2=2:4。
故答案为:1:2=2:4(答案不唯一)。
比例是表示两个比相等的式子。由此写出两个比值是的比,再组成比例即可。
9.12;45;0.6;60;六
解:3÷5=0.6=;
=
=;
0.6=60%;
0.6=六成。
故答案为:12;45;0.6;60;六。
分数的基本性质:分数的分子与分母同时乘或除以相同的数(0除外),分数的大小不变;
整数除法与分数的关系:被除数÷除数=;
比与分数的关系:前项:后项=;
先根据比与分数的关系将比转化成分数形式,再根据分数的基本性质解答即可;
小数转化成百分数:先把小数点向右移动两位,再添上百分号“%”;
成数表示一个数是另一个数的十分之几,通称“几成”。几成改写成百分数就是百分之几十,几成几改写成百分数就是百分之几十几。
10.15;200
解:1-85%=15%,30÷15%=200(元)。
故答案为:15;200。
根据题意可知打八五折即现价是原价的85%,把衣服原价看作单位“1”,1-折扣=便宜的钱占原价的百分比,便宜的钱÷便宜的钱占原价的百分比=衣服原价。
11.188.4;213.52;188.4
解:侧面积:3.14×4×15=188.4(cm );
表面积:188.4+3.14×(4÷2) ×2
=188.4+25.12
=213.52(cm )
体积:3.14×(4÷2) ×15
=3.14×60
=188.4(cm )
故答案为:188.4;213.52;188.4。
用底面周长乘高求出侧面积;根据圆面积公式计算出底面积,用底面积的2倍加上侧面积就是表面积;用底面积乘高即可求出体积。
12.169.56;56.52
解:(6÷2)2×3.14×6=169.56cm3,所以圆柱的体积是169.56cm3;169.56×=56.52cm3,所以圆锥体的体积是56.52cm3。
故答案为:169.56;56.52。
由题意可知,圆锥的底面直径=圆柱的高=正方体的棱长,所以圆柱的体积=(底面直径÷2)2×π×高;把圆柱体削成一个最大的圆锥体,这个圆柱和圆锥等地等高,那么圆锥的体积=圆柱的体积×。
13.两
解:16÷(96-16)×100%
=16÷80×100%
=20%
20%=两成
故答案为:两。
增长百分比 = (增长人数 ÷ 2022年接待人数) × 100%;成数表示一个数是另一个数的十分之几。
14.314cm2
解:3.14×10×10=314(cm2)
故答案为:314cm2。
圆柱的侧面积=底面周长×高,根据公式计算圆柱的侧面积即可。
15.251.2;226.08
解:半径:40÷2÷5
=20÷5
=4(cm);
体积:3.14×42×5
=50.24×5
=251.2(cm3);
表面积:3.14×2×4×5+3.14×42×2
=25.12×5+50.24×2
=125.6+100.48
=226.08(cm2);
故答案为:251.2;226.08。
由图可知,圆柱的高等于长方体的高,增加的40cm2是2个长为底面半径,宽为圆柱的高的长方形面积,因此,用40除以2再除以5即可求出圆柱的半径,再根据圆柱的体积=π×半径2×高,圆柱表面积=侧面积+底面积×2=圆柱周长×高+π×半径2×2,代入数值计算即可。
16.235.5
解:圆柱半径:94.2÷3÷3.14÷2
=31.4÷3.14÷2
=10÷2
=5(厘米);
减少的体积:3.14×52×3
=3.14×25×3
=78.5×3
=235.5(立方厘米);
故答案为:235.5。
由题意可知,圆柱减少的表面积就是长为底面周长,宽为3厘米的长方形面积,据此用减少的表面积除以3即可求出圆柱的底面周长,再根据半径=圆周长÷π÷2求出圆柱的底面半径,最后根据圆柱体积=π×半径2×高代入数值计算即可。
17.(1)5,6,13.5,21.6
(2)正
解:(1)9÷2=4.5(元/千克)
3×4.5=13.5(元),22.5÷4.5=5(千克),4.8×4.5=21.6(元),27÷4.5=6(千克),
数量(千克) 2 3 5 4.8 6
钱数(元) 9 13.5 22.5 21.6 27
(2)应付的钱数÷买苹果的数量=苹果的单价(一定)
买苹果的数量和应付的钱数成正比例。
故答案为:(2)正。
(1)应付的钱数÷买苹果的数量=每千克的钱数,每千克的钱数×买苹果的数量=应付的钱数,应付的钱数÷每千克的钱数=数量;
(2)正比例的判断方法:相关联,能变化,商一定。
18.解:3.14×4×4×(9-7)
=50.24×2
=100.48(立方厘米)
答:这个铁块的体积是100.48立方厘米。
π×底面半径的平方=底面积,底面积×水面上升的高度=这个铁块的体积。
19.0;-3℃
解:0既不是正数,也不是负数,零下3℃记作-3℃。
故答案为:0;-3℃。
正负数表示相反意义的量,高于0℃的温度记作正,低于0℃的温度就记作负。
20.反;15;5
解:反比例图像是一条光滑的曲线;
当高度是20cm,底面积是300÷20=15(cm2);
当底面积是55cm2时,高度是:300÷55≈5(cm)
故答案为:反;15;5。
反比例指的是两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
21.4.5;6.28
解:当圆柱的高是 1.5cm 时,圆锥的高是1.5×3=4.5(cm);
当圆锥的底面积是 18.84cm2时,圆柱的底面积是 18.84÷3=6.28(cm2);
故答案为:4.5;6.28。
等底等高的圆锥体积是圆柱体积的,因此,当圆柱和圆锥体积和底面积分别相等时,圆锥的高是圆柱高的3倍;当圆柱和圆锥的高和体积分别相等时,圆锥的底面积是圆柱底面积的3倍,据此解答。
22.314
解:6.28÷3.14÷2=1(分米)
3.14×1×100
=3.14×100
=314(立方分米)
故答案为:314。
孙悟空的如意金箍棒如果是圆柱形,圆柱的体积 = π × (底面半径的平方) × 高;据此代入数值计算。
23.(1)+4.8;-2.8
(2)26.7;超重
解:(1)21.8-17=4.8,所以男生正常范围的最高值记为+4.8;
17-14.2=2.8,所以女生正常范围的最低值记为-2.8;
(2)BMI=60÷(1.50×1.50)
=60÷2.25
≈26.7;
26.7>21.8,所以他的胖瘦程度是属于超重。
故答案为:(1)+4.8;-2.8;(2)26.7;超重。
(1)根据题意可知,比17高几就记为“+几“,比17低几就记为”-几”;(2)将体重=60,身高=1.50代入到 BMI=体重÷(身高×身高) 中计算即可求出他的BMI值;再根据表格中的数据判断胖瘦程度即可。
24.10;1;40;16
解: 如果a和b成正比例, 那么a:2=20:4=5,所以a=5×2=10;
5:b=20:4=5,b=5÷5=1;
如果a和b成反比例,那么a×2=20×4=80,a=80÷2=40;
5×b=20×4=80,b=80÷5=16;
故答案为:10;1;40;16。
成正比例的两个比的比值相等,即a:2=20:4=5,5:b=20:4=5;成反比例的两个比的乘积相等,即a×2=20×4=80,5×b=20×4=80,据此解答。
25.31.4;20
解:2×π×5
=2×3.14×5
=31.4(cm)
圆柱的高即为商标纸的宽,为20cm。
故答案为:31.4;20。
圆柱的侧面展开后是一个长方形,其长等于圆柱底面的周长,宽等于圆柱的高;圆柱的底面积:S=r2。
26.37.5
解:150÷(3+1)
=150÷4
=37.5(立方米)
故答案为:37.5。
等底等高的圆柱的体积是圆锥体积的3倍,它们的体积之和是(3+1)倍,由此计算圆锥的体积即可。
27.8;226.08
解:3.14×(6÷2)2=28.26(cm2)
75.36÷÷28.26
=226.08÷28.26
=8(cm)
75.36×3=226.08(cm3)
故答案为:8;226.08。
πr2=圆锥的底面积,圆锥的体积÷÷底面积=圆锥的高;
根据圆柱与圆锥体积的关系可知:等底等高的圆柱的体积是圆锥体积的3倍,据此可以解答。
28.64
解:8×4×2
=32×2
=64(cm2)
故答案为:64。
圆柱切开后的一个切面是一个长方形,增加的面积就是2个长是8cm,宽是4cm的长方形的面积。
29.351;51;17%
解:450×78%=351(元)
351-300=51(元)
51÷300=17%。
故答案为:351;51;17%。
售价=标价×折扣;售出这件衣服的利润=售价-进价;利润率=售出这件衣服的利润÷售价。
30.反
解:由=可得:xy=8×5=40, x和y成反比例。
故答案为:反。
比例的基本性质:比例的外项之积等于比例的内项之积;
反比例的判断方法:相关联,能变化,积一定。
31.480
解:表面积比原来增加了2个长方形,
16×15×2
=240×2
=480(平方厘米)
表面积比原来增加480平方厘米。
故答案为:480。
底面直径×长=增加的一个面的面积,增加的一个面的面积×2=增加的面积。
32.13500
解:9000×100×1.5%
=900000×1.5%
=13500(元)
故答案为:13500。
由图可知,购买这套房子需要按1.5%的税率缴纳契税,先用每平方米价格乘房子面积求出房子总价,再乘税率即可解答。
33.
解:在一个比例里,两个内项互为倒数,
可知两个外项也互为倒数,其中一个外项是3,所以另一个外项就是3的倒数 .
故答案为: .
由“在一个比例里,两个内项互为倒数”,根据比例的性质“两外项的积等于两内项的积”,可知两个外项也互为倒数;再根据“其中一个外项是3”,进而求出3的倒数得解.
34.56.52cm3
解:3.14×(6÷2)2×6×
=3.14×9×2
=56.52(cm3)
故答案为:56.52cm3。
把这个正方体削成最大的圆锥,圆锥的底面直径和高都与正方体的棱长相等。圆锥的体积=底面积×高×,根据公式计算圆锥的体积即可。
35.20000;30
比例尺是1:2000000,表示地图上1cm代表实际距离2000000cm,换成m做单位后就是20000m;
600km=60000000cm,60000000×=30(cm)。
故答案为:20000m;30cm。
图上距离:实际距离=比例尺(1:2000000 ) ,就是表示图上1cm代表实际距离2000000cm,但题中的单位是m,所以还要注意化好单位即可;图上距离=实际距离×比例尺(比例尺的分数形式),先将实际距离化成用cm做单位再去求解即可。
36.10:1
解:图上距离是5cm,转换为毫米是5cm ×10 = 50mm,
5cm:5mm
=50mm:5mm
=10:1
故答案为:10:1。
比例尺=图上距离:实际距离;先进行单位换算,再求出比例尺。
37.3:20=6:40
解:把3×40=20×6,改写成比例是3:20=6:40。
故答案为:3:20=6:40。(答案不唯一)
在比例里,两个內项的积等于两个外项的积。把3和40作为外项,20和6就是內项,然后写出比例即可。
38.40;1:4000000
解:在中,图中1cm表示实际距离40km,改写成数值比例尺是1cm:40km=1cm:4000000cm=1:4000000。
故答案为:40;1:4000000。
线段比例尺表示图上1厘米相当于实际距离40千米。写出图上距离与实际距离的比,统一单位后写成前项是1的比就可以改写成数值比例尺。
39.妈妈能获得利息多少元;80000×3×1.95%
解:问题:妈妈能获得利息多少元?
本金是80000元,年利率是1.95%,存款时间为三年,所以利息为:80000×3×1.95%(元)。
故答案为:妈妈能获得利息多少元; 80000×3×1.95%。
利息=本金×利率×存款时间;据此提出问题列出算式。
40.-20;向东行10千米
解:一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作-20千米;+10千米表示向东行10千米。
故答案为:-20;向东行10千米。
以学校为起点,向东走记作正,向西走记作负。根据正负数的意义填空即可。
41.54;47;50
甲:50+4=54(kg);
乙:50-3=47(kg);
丙跟标准一样,就是50kg。
故答案为:54kg;47kg;50kg。
这个题还是关于正负数的意义,题中已经规定50kg为0kg,找准这个标准,然后理解:+4kg就表示在标准的基础上加4kg,同样的-3kg在标准上减3kg,而0kg跟标准一样即可做出答案。
42.25.12cm
解:3.14×8=25.12(cm)
故答案为:25.12cm。
圆柱的侧面展开是正方形,那么圆柱的高与底面周长相等,所以计算出圆柱的底面周长就是这个圆柱的高。
43.20
解:16÷=80000000(厘米)
80000000×=20(厘米)
故答案为:20。
依据“实际距离=图上距离÷比例尺”即可求出南昌、广州两地的实际距离,再根据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离。
44.628
解:3.14×102×6×
=314×6×
=314×2
=628(立方厘米)
故答案为:628。
将这个直角三角形以6厘米为轴旋转一周,可得到一个以6厘米为高、以10厘米为底面半径的圆锥体,根据圆锥的体积公式V=sh进行计算。
45.0.18
解:10dm=100cm
3.6÷2×100
=1.8×100
=180(立方厘米)
180立方厘米=0.18立方分米
故答案为:0.18。
把一根长10dm的圆柱形钢柱截成两段 ,增加了2个面,每个面积都是圆柱的底面积,用3.6除以2求出圆柱的底面积,再根据圆柱的体积公式V=Sh,求出圆柱的体积,再换算单位。
46.90;80
解: “九折”表示现价相当于原价的90%。
72÷90%=80(元)
故答案为:90;80。
打几折,表示现价是原价的百分之几十;用现价÷折扣=原价。
47.4;-4;8℃
解:4-(-4℃)=8℃
这天的最高气温是4℃,最低气温是-4℃,温差是8℃。
故答案为:4;-4;8℃。
气温高于0℃记作正,则低于0℃就记作负。用最高气温减去最低气温求出温差。
48.圆锥;226.08
解:技术人员用一个直角三角形(如图),绕着一条直角 边旋转成一个圆锥;
它的体积是3.14×62×6×
=3.14×36×6×
=113.04×2
=226.08(cm3)
故答案为:226.08。
一个直角三角形,绕着一条直角边旋转得到的是一个圆锥,这个三角形是个等腰直角三角形,所以得到的圆锥的底面半径和高都是6厘米,再根据圆锥体积=π×半径2×高×,代入数值计算解答。
49.4
解:2÷=4;
故答案为:4。
比例的基本性质:内项积等于外项积,因此,两个内项是最小的质数2,两个外项的乘积也是2,用两个外项的积除以一个已知的外项即可求出另一个外项。
50.7.065
解:3÷2=1.5(分米)
3.14×1.5×1.5×3×
=7.065×3×
=7.065(立方分米)
故答案为:7.065。
将正方体木块削成一个最大的圆锥体,这个圆锥的底面直径=正方体的棱长,高=正方体的棱长,这个圆锥体的体积=π×半径×半径×高×。
期中考试真题分类汇编11 填空题
一、填空题
1.(2024六下·江门期中)把2米长的圆柱形木棒锯成三段,表面积增加了40dm3,原来木棒的体积是 dm3
2.(2024六下·鹰潭期中)如果a与b互为倒数,并且那么c= ,= 。
3.(2024六下·玉田期中)实验小学六⑴班学生的平均体重是39千克,如表所示是该班5名学生的体重统计表
学号 1 2 3 4 5
体重(千克) 35 39 50
与平均体重相比(千克) ﹣4 +5 ﹣7
4.(2024六下·江门期中)在一幅比例尺是1:20000000的地图上,量得甲乙两地的距离为3.04 厘米,那么这两地的实际距离是 千米:如果汽车每小时行驶 80千米,从甲地到乙地要 小时。
5.(2024六下·大余期中)用一张长15cm,宽12cm的长方形纸围成一个圆柱,圆柱的侧面积是 cm2。
6.(2024六下·江门期中)甲数的等于乙数的 (甲、乙均不为0),甲数与乙数的比是 。
7.(2024六下·江门期中)用18的因数写出一个比例是 。
8.(2024六下·鹰潭期中)写出两个比值都是的比,再组成比例是 。
9.(2024六下·江门期中)3÷5= :20= = (填小数)= %= 成。
10.(2024六下·江门期中)一件衣服打八五折出售,也就是便宜 %,便宜了30元,衣服原价是 元。
11.(2024六下·江门期中)一个圆柱的底面直径是4cm,高是15cm,它的侧面积是 cm2,表面积是 cm2,体积是 cm3.
12.(2024六下·江门期中)一个正方体木块的棱长是6cm,把它削成一个最大的圆柱体。圆柱体的体积是 cm3。再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积是 cm3。
13.(2024六下·瑞金期中)某市2023年接待旅游总人数约为96万人次,比上一年增长约16万人次。该市2023年接待旅游总人数比2022年增长 成。
14.(2024六下·鹰潭期中)一个圆柱的底面直径和高都是10cm,这个圆柱的侧面积是 。
15.(2024六下·南海期中)如图把圆柱沿高切成若干偶数等份,拼起来就是一个近似的长方体。这个长方体的高为 5cm,它的表面积比圆柱多 40cm2。圆柱的体积是 cm3,表面 积是 cm2。
16.(2024六下·徐闻期中)一个圆柱,如果把它的高截短3cm,表面积就减少94.2cm2,体积就减少 cm3。
17.(2024六下·玉田期中)如表所示是李叔叔四月份购买苹果的记录单。
数量(千克) 2 3 4.8
钱数(元) 9 22.5 27
(1)苹果的单价一定,请在表中空白处填上合适的数。
(2)买苹果的数量和应付的钱数成 比例。
18.(2024六下·玉田期中)把一个铁块放入下面的水杯中,水面的变化如图所示,这个铁块的体积是立方厘米。
19.(2024六下·鹰潭期中) 既不是正数,也不是负数,零下3℃记作 。
20.(2024六下·瑞金期中)如下图图象是光滑的曲线,可知图中的两种量成 比例关系。由如图图象,可以看出容器:底面积是 cm2时,高是20cm。底面积是55cm2时,高是 cm。
21.(2024六下·南海期中)如果圆柱和圆锥的底面积和体积分别相等,当圆柱的高是 1.5cm 时,圆锥的高是 cm;如果圆柱和圆锥的高和体积分别相等,当圆锥的底面积是 18.84cm2时,圆柱的底 面积是 cm2。
22.(2024六下·瑞金期中)西游记中的孙悟空正直勇敢、嫉恶如仇,他有一件神奇的兵器叫如意金箍棒,可以任意缩小或放大。如果孙悟空把如意金箍棒变化成底面周长是6.28分米,长是100分米的圆柱形铁棒,那么此时,它的体积是 立方分米。
23.(2024六下·南海期中)BMI 指数是衡量人体胖瘦程度及是否健康的常用指标,计算公式:BMI=体重÷(身高×身高),下表 是六年级学生的 BMI 正常值范围。低于正常范围为消瘦,高于正常范围的为超重。(体重单位:kg;身高单 位:m)
规定 BMI 为 17 是 0 点,高于 17 为正,低于 17 为负。
男生 14.7~21.8
女生 14.2~20.8
(1)用正、负数表示 BMI 指数的正常范围,男生正常范围的最高值记为 ,女生正常范围的最低值记为 。
(2)小明是一个六年级的男孩子,他的体重是 60 kg,身高 1.50 米,他的 BMI 值是 (结果保留一位小数)。根据他的 BMI 指数,判断他的胖瘦程度是属于 。(填“消瘦”、“正常”或“超重”)
24.(2024六下·徐闻期中)在下图表格中,如果a和b成正比例,那么a填 b填 ;如果a和b成反比例,那么a填 ,b填 。
a 20 5
b 4 2
25.(2024六下·瑞金期中)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,它的长是 cm,宽是 cm。
26.(2024六下·大余期中)等底等高的圆柱和圆锥体,它们的体积之和是150立方米,圆锥的体积是 立方米。
27.(2024六下·南昌期中)一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是 cm,和它等底等高的圆柱的体积是 cm3。
28.(2024六下·瑞金期中)如下图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了 平方厘米。
29.(2024六下·万载期中) 一件外套标价450元,按七八折售出,售价是 元。如果这件衣服进价是300元,售出这件衣服的利润是 元,利润率是 。
30.(2024六下·玉田期中)当=(y≠0)时,x和y成 比例。
31.(2024六下·玉田期中)把一个底面直径是16厘米,长是15厘米的圆柱形木头沿着底面直径竖直锯开后,表面积比原来增加 平方厘米。
32.(2024六下·南海期中)某新建商品房开售,每平方米 9000 元,阳阳的爸爸购买了一 套 100m2的房子,需要缴纳一定的契税(缴纳标准如图)。购买这套房子 一共需要缴纳 元的契税。
契税 新建商品房按房屋总价 的 1.5%征收,购买 90m2及以 下的普通住房,契税按1%征收。
33.(2024六下·陆川期中)在一个比例里,两个内项互为倒数,其中一个外项是3,另一个外项是 .
34.(2024六下·鹰潭期中)把一个棱长是6cm的正方体削成一个最大的圆锥体,这个圆锥的体积是 。
35.(2024六下·南华期中)一幅地图的比例尺是1:2000000,它表示地图上的1cm代表实际的 m。若甲、乙两地相距600km,在这幅地图上应该画 cm。
36.(2024六下·瑞金期中) 一张精密仪器图纸,用5cm长表示实际长5mm,则这幅图的比例尺是 。
37.(2024六下·鹰潭期中)把3×40=20×6,改写成比例是 。
38.(2024六下·鹰潭期中)在中,图中1cm表示实际距离 km,改写成数值比例尺是 。
39.(2024六下·瑞金期中)妈妈把80000元存入银行,存期为三年定期,年利率1.95%。请提出数学问题: ,列出算式: 。
40.(2024六下·鹰潭期中)一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作 千米;+10千米表示 。
41.(2024六下·南华期中)若把六年级学生的平均体重50kg记作0kg,甲、乙、丙三名同学的体重被分别记为+4kg、-3kg、0kg,则他们三人的实际体重分别是 kg、 kg、 kg。
42.(2024六下·鹰潭期中)把一个圆柱侧面展开,得到一个正方形,这个圆柱的底面直径是8cm,圆柱的高是 。
43.(2024六下·大余期中)在比例尺为1:5000000的地图上,南昌、广州两地相距16cm,在另一幅比例尺为1:4000000的地图上,南昌、广州两地相距 厘米。
44.(2024六下·大余期中)一个直角三角形的两条直角边分别为6cm,10cm,若以6cm的边为轴旋转一周,所围图形的体积是 cm3。
45.(2024六下·大余期中)把一根长10dm的圆柱形钢柱截成两段,表面积比原来增加:,这根圆柱原来的体积是 dm3。
46.(2024六下·大余期中)天虹超市举行“五一”商品大推销,有一套“”玩具打九折出售,“九折”表示现价相当于原价的 %,如果这件玩具现价卖72元,那么原价是 。
47.(2024六下·大余期中)某地某日的气温是-4℃~4℃,这表明这天的最高气温是 ℃,最低气温是 ℃,温差是 。
48.(2024六下·南海期中)3D 电脑动画成像技术展示活动中,技术人员用一个直角三角形(如图),绕着一条直角 边旋转成一个 ,它的体积是 cm3。
49.(2024六下·南海期中)在一个比例中,两个内项的积是最小的质数,已知一个外项是,另一个外项是 。
50.(2024六下·徐闻期中)将一个棱长为3dm的正方体木块削成一个最大的圆锥体,这个圆锥体的体积为 dm3。
答案解析部分
1.200
解:2米=20分米
(3-1)×2=4(个)
40÷4=10(平方分米)
10×20=200(立方分米)
故答案为:200。
通过实际操作可知每锯一次就增加2个底面,因此根据题意可得:段数-1=锯的次数,(段数-1)×2=增加的底面个数,增加的表面积÷增加的底面个数=圆柱形木棒的底面积,圆柱形木棒的底面积×长=原木棒的体积;计算时统一单位:1米=10分米,大单位转化成小单位乘进率。
2.;
解:则ab=5c,ab=1,所以5c=1,则c=;
=×=。
故答案为:;。
根据比例的基本性质把这个比例写成两个內项积等于两个外项积的行驶,a与b互为倒数,则a、b的积是1,这样就能求出c的值,然后求出的值即可。
3.44;32;0;+11
解:第一空:39+5=44(千克)
第二空:39-7=32(千克)
第三空:39-39=0(千克)
第四空:50-39=11(千克)
学号 1 2 3 4 5
体重(千克) 35 44 39 50 32
与平均体重相比(千克) ﹣4 +5 0 +11 ﹣7
故答案为:44;32;0;+11。
比39千克多的质量用正数表示,比39千克少的质量用负数表示,正数表示比39千克多的质量,负数表示比39千克少的质量,据此解答。
4.608;7.6
解:3.04÷=60800000(厘米)
60800000厘米=608千米;
608÷80=7.6(小时)
故答案为:608;7.6。
根据题意可得:图上距离÷比例尺=实际距离,实际距离÷汽车的速度=需要的时间;在计算时统一单位:1千米=100000厘米,小单位转化成大单位除以进率。
5.180
解:15×12=180(平方厘米)
故答案为:180。
根据圆柱的侧面展开图的特点:圆柱的底面周长是长方形的长,圆柱的高是长方形的宽,所以这个圆柱的侧面积就是这个长方形的面积;用长乘宽即可。
6.5:18
解::
=(×30):(×30)
=5:18
故答案为:5:18。
因为,甲数×=乙数×,所以,根据比例的基本性质:两个外项的积等于两个内项的积,可得:甲数:乙数=:,再化简即可。
7.2:3=6:9
解:18的因数有1,2,3,6,9,18,即2×9=3×6,所以2:3=6:9。
故答案为:2:3=6:9。
求一个数的因数可以通过从1开始想哪两个数相乘等于这个数,那么这两个因数就都是这个数的因数;也可以通过用这个数从1开始除以一个数,找到没有余数的商和除数,就都是这个数的因数。1和它本身也是这个数的因数;
比例的基本性质:两个外项的积等于两个内项的积;
先根据因数找法找到18的因数,再找到乘积相等的算式,最后根据比例的基本性质即可写比例。
8.1:2=2:4
解:写出两个比值都是的比,再组成比例是1:2=2:4。
故答案为:1:2=2:4(答案不唯一)。
比例是表示两个比相等的式子。由此写出两个比值是的比,再组成比例即可。
9.12;45;0.6;60;六
解:3÷5=0.6=;
=
=;
0.6=60%;
0.6=六成。
故答案为:12;45;0.6;60;六。
分数的基本性质:分数的分子与分母同时乘或除以相同的数(0除外),分数的大小不变;
整数除法与分数的关系:被除数÷除数=;
比与分数的关系:前项:后项=;
先根据比与分数的关系将比转化成分数形式,再根据分数的基本性质解答即可;
小数转化成百分数:先把小数点向右移动两位,再添上百分号“%”;
成数表示一个数是另一个数的十分之几,通称“几成”。几成改写成百分数就是百分之几十,几成几改写成百分数就是百分之几十几。
10.15;200
解:1-85%=15%,30÷15%=200(元)。
故答案为:15;200。
根据题意可知打八五折即现价是原价的85%,把衣服原价看作单位“1”,1-折扣=便宜的钱占原价的百分比,便宜的钱÷便宜的钱占原价的百分比=衣服原价。
11.188.4;213.52;188.4
解:侧面积:3.14×4×15=188.4(cm );
表面积:188.4+3.14×(4÷2) ×2
=188.4+25.12
=213.52(cm )
体积:3.14×(4÷2) ×15
=3.14×60
=188.4(cm )
故答案为:188.4;213.52;188.4。
用底面周长乘高求出侧面积;根据圆面积公式计算出底面积,用底面积的2倍加上侧面积就是表面积;用底面积乘高即可求出体积。
12.169.56;56.52
解:(6÷2)2×3.14×6=169.56cm3,所以圆柱的体积是169.56cm3;169.56×=56.52cm3,所以圆锥体的体积是56.52cm3。
故答案为:169.56;56.52。
由题意可知,圆锥的底面直径=圆柱的高=正方体的棱长,所以圆柱的体积=(底面直径÷2)2×π×高;把圆柱体削成一个最大的圆锥体,这个圆柱和圆锥等地等高,那么圆锥的体积=圆柱的体积×。
13.两
解:16÷(96-16)×100%
=16÷80×100%
=20%
20%=两成
故答案为:两。
增长百分比 = (增长人数 ÷ 2022年接待人数) × 100%;成数表示一个数是另一个数的十分之几。
14.314cm2
解:3.14×10×10=314(cm2)
故答案为:314cm2。
圆柱的侧面积=底面周长×高,根据公式计算圆柱的侧面积即可。
15.251.2;226.08
解:半径:40÷2÷5
=20÷5
=4(cm);
体积:3.14×42×5
=50.24×5
=251.2(cm3);
表面积:3.14×2×4×5+3.14×42×2
=25.12×5+50.24×2
=125.6+100.48
=226.08(cm2);
故答案为:251.2;226.08。
由图可知,圆柱的高等于长方体的高,增加的40cm2是2个长为底面半径,宽为圆柱的高的长方形面积,因此,用40除以2再除以5即可求出圆柱的半径,再根据圆柱的体积=π×半径2×高,圆柱表面积=侧面积+底面积×2=圆柱周长×高+π×半径2×2,代入数值计算即可。
16.235.5
解:圆柱半径:94.2÷3÷3.14÷2
=31.4÷3.14÷2
=10÷2
=5(厘米);
减少的体积:3.14×52×3
=3.14×25×3
=78.5×3
=235.5(立方厘米);
故答案为:235.5。
由题意可知,圆柱减少的表面积就是长为底面周长,宽为3厘米的长方形面积,据此用减少的表面积除以3即可求出圆柱的底面周长,再根据半径=圆周长÷π÷2求出圆柱的底面半径,最后根据圆柱体积=π×半径2×高代入数值计算即可。
17.(1)5,6,13.5,21.6
(2)正
解:(1)9÷2=4.5(元/千克)
3×4.5=13.5(元),22.5÷4.5=5(千克),4.8×4.5=21.6(元),27÷4.5=6(千克),
数量(千克) 2 3 5 4.8 6
钱数(元) 9 13.5 22.5 21.6 27
(2)应付的钱数÷买苹果的数量=苹果的单价(一定)
买苹果的数量和应付的钱数成正比例。
故答案为:(2)正。
(1)应付的钱数÷买苹果的数量=每千克的钱数,每千克的钱数×买苹果的数量=应付的钱数,应付的钱数÷每千克的钱数=数量;
(2)正比例的判断方法:相关联,能变化,商一定。
18.解:3.14×4×4×(9-7)
=50.24×2
=100.48(立方厘米)
答:这个铁块的体积是100.48立方厘米。
π×底面半径的平方=底面积,底面积×水面上升的高度=这个铁块的体积。
19.0;-3℃
解:0既不是正数,也不是负数,零下3℃记作-3℃。
故答案为:0;-3℃。
正负数表示相反意义的量,高于0℃的温度记作正,低于0℃的温度就记作负。
20.反;15;5
解:反比例图像是一条光滑的曲线;
当高度是20cm,底面积是300÷20=15(cm2);
当底面积是55cm2时,高度是:300÷55≈5(cm)
故答案为:反;15;5。
反比例指的是两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
21.4.5;6.28
解:当圆柱的高是 1.5cm 时,圆锥的高是1.5×3=4.5(cm);
当圆锥的底面积是 18.84cm2时,圆柱的底面积是 18.84÷3=6.28(cm2);
故答案为:4.5;6.28。
等底等高的圆锥体积是圆柱体积的,因此,当圆柱和圆锥体积和底面积分别相等时,圆锥的高是圆柱高的3倍;当圆柱和圆锥的高和体积分别相等时,圆锥的底面积是圆柱底面积的3倍,据此解答。
22.314
解:6.28÷3.14÷2=1(分米)
3.14×1×100
=3.14×100
=314(立方分米)
故答案为:314。
孙悟空的如意金箍棒如果是圆柱形,圆柱的体积 = π × (底面半径的平方) × 高;据此代入数值计算。
23.(1)+4.8;-2.8
(2)26.7;超重
解:(1)21.8-17=4.8,所以男生正常范围的最高值记为+4.8;
17-14.2=2.8,所以女生正常范围的最低值记为-2.8;
(2)BMI=60÷(1.50×1.50)
=60÷2.25
≈26.7;
26.7>21.8,所以他的胖瘦程度是属于超重。
故答案为:(1)+4.8;-2.8;(2)26.7;超重。
(1)根据题意可知,比17高几就记为“+几“,比17低几就记为”-几”;(2)将体重=60,身高=1.50代入到 BMI=体重÷(身高×身高) 中计算即可求出他的BMI值;再根据表格中的数据判断胖瘦程度即可。
24.10;1;40;16
解: 如果a和b成正比例, 那么a:2=20:4=5,所以a=5×2=10;
5:b=20:4=5,b=5÷5=1;
如果a和b成反比例,那么a×2=20×4=80,a=80÷2=40;
5×b=20×4=80,b=80÷5=16;
故答案为:10;1;40;16。
成正比例的两个比的比值相等,即a:2=20:4=5,5:b=20:4=5;成反比例的两个比的乘积相等,即a×2=20×4=80,5×b=20×4=80,据此解答。
25.31.4;20
解:2×π×5
=2×3.14×5
=31.4(cm)
圆柱的高即为商标纸的宽,为20cm。
故答案为:31.4;20。
圆柱的侧面展开后是一个长方形,其长等于圆柱底面的周长,宽等于圆柱的高;圆柱的底面积:S=r2。
26.37.5
解:150÷(3+1)
=150÷4
=37.5(立方米)
故答案为:37.5。
等底等高的圆柱的体积是圆锥体积的3倍,它们的体积之和是(3+1)倍,由此计算圆锥的体积即可。
27.8;226.08
解:3.14×(6÷2)2=28.26(cm2)
75.36÷÷28.26
=226.08÷28.26
=8(cm)
75.36×3=226.08(cm3)
故答案为:8;226.08。
πr2=圆锥的底面积,圆锥的体积÷÷底面积=圆锥的高;
根据圆柱与圆锥体积的关系可知:等底等高的圆柱的体积是圆锥体积的3倍,据此可以解答。
28.64
解:8×4×2
=32×2
=64(cm2)
故答案为:64。
圆柱切开后的一个切面是一个长方形,增加的面积就是2个长是8cm,宽是4cm的长方形的面积。
29.351;51;17%
解:450×78%=351(元)
351-300=51(元)
51÷300=17%。
故答案为:351;51;17%。
售价=标价×折扣;售出这件衣服的利润=售价-进价;利润率=售出这件衣服的利润÷售价。
30.反
解:由=可得:xy=8×5=40, x和y成反比例。
故答案为:反。
比例的基本性质:比例的外项之积等于比例的内项之积;
反比例的判断方法:相关联,能变化,积一定。
31.480
解:表面积比原来增加了2个长方形,
16×15×2
=240×2
=480(平方厘米)
表面积比原来增加480平方厘米。
故答案为:480。
底面直径×长=增加的一个面的面积,增加的一个面的面积×2=增加的面积。
32.13500
解:9000×100×1.5%
=900000×1.5%
=13500(元)
故答案为:13500。
由图可知,购买这套房子需要按1.5%的税率缴纳契税,先用每平方米价格乘房子面积求出房子总价,再乘税率即可解答。
33.
解:在一个比例里,两个内项互为倒数,
可知两个外项也互为倒数,其中一个外项是3,所以另一个外项就是3的倒数 .
故答案为: .
由“在一个比例里,两个内项互为倒数”,根据比例的性质“两外项的积等于两内项的积”,可知两个外项也互为倒数;再根据“其中一个外项是3”,进而求出3的倒数得解.
34.56.52cm3
解:3.14×(6÷2)2×6×
=3.14×9×2
=56.52(cm3)
故答案为:56.52cm3。
把这个正方体削成最大的圆锥,圆锥的底面直径和高都与正方体的棱长相等。圆锥的体积=底面积×高×,根据公式计算圆锥的体积即可。
35.20000;30
比例尺是1:2000000,表示地图上1cm代表实际距离2000000cm,换成m做单位后就是20000m;
600km=60000000cm,60000000×=30(cm)。
故答案为:20000m;30cm。
图上距离:实际距离=比例尺(1:2000000 ) ,就是表示图上1cm代表实际距离2000000cm,但题中的单位是m,所以还要注意化好单位即可;图上距离=实际距离×比例尺(比例尺的分数形式),先将实际距离化成用cm做单位再去求解即可。
36.10:1
解:图上距离是5cm,转换为毫米是5cm ×10 = 50mm,
5cm:5mm
=50mm:5mm
=10:1
故答案为:10:1。
比例尺=图上距离:实际距离;先进行单位换算,再求出比例尺。
37.3:20=6:40
解:把3×40=20×6,改写成比例是3:20=6:40。
故答案为:3:20=6:40。(答案不唯一)
在比例里,两个內项的积等于两个外项的积。把3和40作为外项,20和6就是內项,然后写出比例即可。
38.40;1:4000000
解:在中,图中1cm表示实际距离40km,改写成数值比例尺是1cm:40km=1cm:4000000cm=1:4000000。
故答案为:40;1:4000000。
线段比例尺表示图上1厘米相当于实际距离40千米。写出图上距离与实际距离的比,统一单位后写成前项是1的比就可以改写成数值比例尺。
39.妈妈能获得利息多少元;80000×3×1.95%
解:问题:妈妈能获得利息多少元?
本金是80000元,年利率是1.95%,存款时间为三年,所以利息为:80000×3×1.95%(元)。
故答案为:妈妈能获得利息多少元; 80000×3×1.95%。
利息=本金×利率×存款时间;据此提出问题列出算式。
40.-20;向东行10千米
解:一辆汽车从学校向东走21千米记作+21千米,那么汽车从学校向西行20千米可以记作-20千米;+10千米表示向东行10千米。
故答案为:-20;向东行10千米。
以学校为起点,向东走记作正,向西走记作负。根据正负数的意义填空即可。
41.54;47;50
甲:50+4=54(kg);
乙:50-3=47(kg);
丙跟标准一样,就是50kg。
故答案为:54kg;47kg;50kg。
这个题还是关于正负数的意义,题中已经规定50kg为0kg,找准这个标准,然后理解:+4kg就表示在标准的基础上加4kg,同样的-3kg在标准上减3kg,而0kg跟标准一样即可做出答案。
42.25.12cm
解:3.14×8=25.12(cm)
故答案为:25.12cm。
圆柱的侧面展开是正方形,那么圆柱的高与底面周长相等,所以计算出圆柱的底面周长就是这个圆柱的高。
43.20
解:16÷=80000000(厘米)
80000000×=20(厘米)
故答案为:20。
依据“实际距离=图上距离÷比例尺”即可求出南昌、广州两地的实际距离,再根据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离。
44.628
解:3.14×102×6×
=314×6×
=314×2
=628(立方厘米)
故答案为:628。
将这个直角三角形以6厘米为轴旋转一周,可得到一个以6厘米为高、以10厘米为底面半径的圆锥体,根据圆锥的体积公式V=sh进行计算。
45.0.18
解:10dm=100cm
3.6÷2×100
=1.8×100
=180(立方厘米)
180立方厘米=0.18立方分米
故答案为:0.18。
把一根长10dm的圆柱形钢柱截成两段 ,增加了2个面,每个面积都是圆柱的底面积,用3.6除以2求出圆柱的底面积,再根据圆柱的体积公式V=Sh,求出圆柱的体积,再换算单位。
46.90;80
解: “九折”表示现价相当于原价的90%。
72÷90%=80(元)
故答案为:90;80。
打几折,表示现价是原价的百分之几十;用现价÷折扣=原价。
47.4;-4;8℃
解:4-(-4℃)=8℃
这天的最高气温是4℃,最低气温是-4℃,温差是8℃。
故答案为:4;-4;8℃。
气温高于0℃记作正,则低于0℃就记作负。用最高气温减去最低气温求出温差。
48.圆锥;226.08
解:技术人员用一个直角三角形(如图),绕着一条直角 边旋转成一个圆锥;
它的体积是3.14×62×6×
=3.14×36×6×
=113.04×2
=226.08(cm3)
故答案为:226.08。
一个直角三角形,绕着一条直角边旋转得到的是一个圆锥,这个三角形是个等腰直角三角形,所以得到的圆锥的底面半径和高都是6厘米,再根据圆锥体积=π×半径2×高×,代入数值计算解答。
49.4
解:2÷=4;
故答案为:4。
比例的基本性质:内项积等于外项积,因此,两个内项是最小的质数2,两个外项的乘积也是2,用两个外项的积除以一个已知的外项即可求出另一个外项。
50.7.065
解:3÷2=1.5(分米)
3.14×1.5×1.5×3×
=7.065×3×
=7.065(立方分米)
故答案为:7.065。
将正方体木块削成一个最大的圆锥体,这个圆锥的底面直径=正方体的棱长,高=正方体的棱长,这个圆锥体的体积=π×半径×半径×高×。
同课章节目录
