期中考试真题分类汇编12 填空题(含答案+解析)---2024-2025学年苏教版六年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编12 填空题(含答案+解析)---2024-2025学年苏教版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 07:47:08 | ||
图片预览




文档简介
2024-2025学年苏教版六年级数学下册
期中考试真题分类汇编12 填空题
一、填空题
1.(2024六下·徐闻期中)根据4×6=3×8,写成一个比例式是 。
2.(2024六下·汉川期中)某服装店一件休闲装现价200元,比原价少了50元,相当于打了 折。照这样的折扣,原价800元的西装,现价 元。
3.(2024六下·七星关期中)一个圆柱和一个圆锥的体积相等,高也相等,已知圆柱的底面积是18平方厘米,圆锥的底面积是 平方厘米。
4.(2024六下·雷州期中)把一个底面周长大约 60cm 的圆柱沿着直径垂直底面切成两个半圆柱,表面积增加了 80cm3,这个圆柱的体积是 cm3。
5.(2024六下·徐闻期中)一幅图的比例尺是,这个比例尺用数值比例尺表示为 ;A、B两地相距80km,画在这幅图上应是 cm。
6.(2024六下·黄石期中)将一个底面半径4厘米的圆柱切拼成一个近似的长方体(如下图),其表面积增加了48cm2,圆柱的体积是 立方厘米。
7.(2024六下·徐闻期中)一个圆柱体的底面周长是12.56cm,高4cm,它的侧面积是 cm2。
8.(2024六下·隆回期中)如图,本次视力检测中,近视人数与视力正常人数的最简整数比是 。如果本次视力检测中,六年级视力正常的共有126人,近视学生有 人。
9.(2024六下·汝城期中)测量小组测量水塔的高度,量得水塔影长是22.5m,同时同地量得附近一根3m 长的标杆的影长是45m,那么水塔高 m。
10.(2024六下·汉川期中)王红把下图中的长方体橡皮泥捏成一个高是8cm的圆柱,捏成的圆柱的底面积是 cm2.如果捏成与圆柱底面相等的圆锥,这个圆锥的高是 cm。
11.(2024六下·汉川期中)下表中a和b是两种相关联的量。
a 30 m
b 6 50
(1)当m=250时,a和b成 比例.
(2)当m= 时,a和b成反比例.
12.(2024六下·汉川期中)“一带一路”沿线国家之一俄罗斯,某月的日均最高气温是零下12℃,可记作 ℃.我国海南自贸区该月的日均最高气温是24℃,可记作 ℃.
13.(2024六下·隆回期中)一个圆柱的底面直径是8厘米,高是5厘米,它的表面积是 平方厘米,体积是 立方厘米。
14.(2024六下·雷州期中)圆的周长与直径 比例,如果圆的周长一定,它的直径和圆周率 比例,
如果圆的直径一定,它的周长和周周率 比例。(填“成正”、“成反”或“不成”)
15.(2024六下·汝城期中)一幅平面图上的比例尺是50:1,表示 距离是 距离的50倍。
16.(2024六下·汝城期中) 李阿姨10月份工资收入为5000元,记作+5000元, 理财收入2500元,记作 ; 而当月支出费用3800元, 记作 。
17.(2024六下·雷州期中)在一个比例里,两个内项的积为最小的合数,一个外项为,另一个外项是 。
18.(2024六下·岷县期中)一个圆柱的侧面积是1570cm2,高是50cm,它的底面周长是 cm,底面的半径是 cm。
19.(2024六下·隆回期中)一个圆锥和它等底等高的圆柱的体积相差9.6立方厘米,圆柱的体积是 立方厘米,圆锥的体积是 立方厘米。
20.(2024六下·汉川期中)3÷4= = = %= 折= (填成数)
21.(2024六下·齐河期中)一支钢笔,打八折卖出亏10元,打九折卖出赚15元,则这件商品的标价是 元,若卖18元,可赚 元。
22.(2024六下·汉川期中)有一块长28.26厘米、宽15.7厘米的长方形铁皮,应配上直径 厘米的圆形铁皮,可以做成一个容积最大的圆柱体。
23.(2024六下·雷州期中)在下表中,如果和y成正比例,a是 ,如果和y成反比例,a是 。
x 4 5
y 20 a
24.(2024六下·徐闻期中)在比例里,两个内项的积是最小的合数,一个外项是4,另一个外项是 。
25.(2023六下·惠来期中)如图,把圆柱切开,拼成一个近似的长方体,量得长方体的长是12.56cm,高是10cm,这个圆柱的体积是 立方厘米。
26.(2024六下·徐闻期中)如果,那么x:y= : ,x和y成 比例。
27.(2024六下·汝城期中)一件商品打八折销售,原价1400元,那么便宜了 元。
28.(2024六下·七星关期中)把一个高是15厘米的圆柱平均切成若干等份,如右图所示,拼成一个近似的长方体,如果拼成的长方体的表面积比圆柱增加了60平方厘米,原来圆柱的体积是 立方厘米。
29.(2024六下·汝城期中) 如果A×B=C(A、B均不为0), 那么A:C= :B。
30.(2024六下·七星关期中)一个直角三角形的两条直角边分别是3厘米和4厘米,如果以它的一条直角边为轴,旋转一周,可以得到一个 ,它的体积最大是 立方厘米。
31.(2024六下·七星关期中)做一节底面半径是10厘米、长是50厘米的圆柱形烟囱,至少需要 平方分米的铁皮。
32.(2024六下·徐闻期中)一个圆柱体水桶(无盖),已知底面半径是2分米,高为3分米,那么做一个这样的水桶至少需要铁皮 dm2,最多可以装水 dm3。
33.(2024六下·七星关期中)从正面观察一个圆柱,看到的形状是一个边长是20厘米的正方形,这个圆柱的表面积是 平方厘米,体积是 立方厘米。
34.(2024六下·汝城期中)将一个底面直径是8cm,高是5cm的圆柱切成两个完全相等的部分,沿直径垂直切下,表面积增加 cm2,沿平行于底面横切,表面积增加 cm2。
35.(2024六下·七星关期中)一根圆柱形木料,底面直径是6分米,高是10分米,沿底面直径把它锯成完全一样的两块,表面积增加了 平方分米。
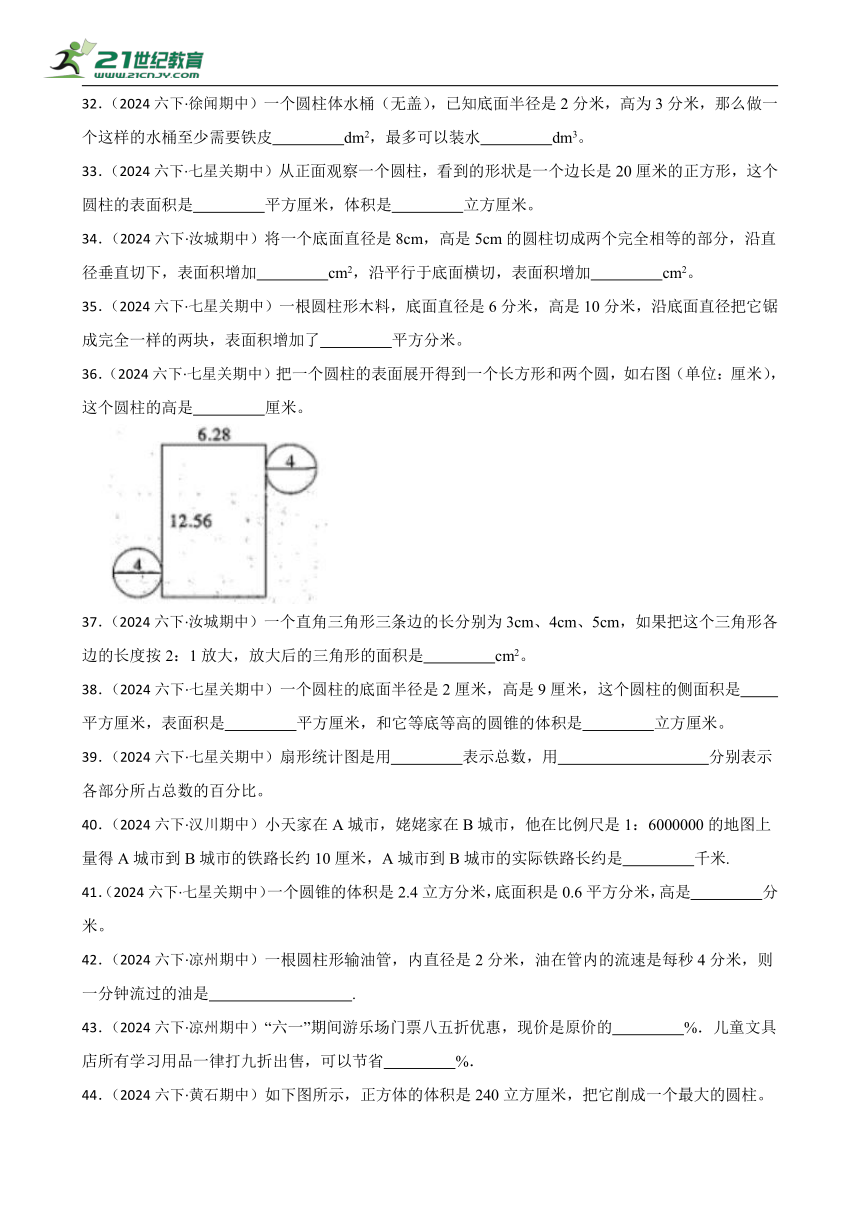
36.(2024六下·七星关期中)把一个圆柱的表面展开得到一个长方形和两个圆,如右图(单位:厘米),这个圆柱的高是 厘米。
37.(2024六下·汝城期中)一个直角三角形三条边的长分别为3cm、4cm、5cm,如果把这个三角形各边的长度按2:1放大,放大后的三角形的面积是 cm2。
38.(2024六下·七星关期中)一个圆柱的底面半径是2厘米,高是9厘米,这个圆柱的侧面积是 平方厘米,表面积是 平方厘米,和它等底等高的圆锥的体积是 立方厘米。
39.(2024六下·七星关期中)扇形统计图是用 表示总数,用 分别表示各部分所占总数的百分比。
40.(2024六下·汉川期中)小天家在A城市,姥姥家在B城市,他在比例尺是1:6000000的地图上量得A城市到B城市的铁路长约10厘米,A城市到B城市的实际铁路长约是 千米.
41.(2024六下·七星关期中)一个圆锥的体积是2.4立方分米,底面积是0.6平方分米,高是 分米。
42.(2024六下·凉州期中)一根圆柱形输油管,内直径是2分米,油在管内的流速是每秒4分米,则一分钟流过的油是 .
43.(2024六下·凉州期中)“六一”期间游乐场门票八五折优惠,现价是原价的 %.儿童文具店所有学习用品一律打九折出售,可以节省 %.
44.(2024六下·黄石期中)如下图所示,正方体的体积是240立方厘米,把它削成一个最大的圆柱。圆柱体积是 立方厘米。
45.(2024六下·雷州期中)一个直角三角形的两条直角边分别为3cm和6cm,现在以其中一条直角边为轴旋转一周得到一个尽可能大的圆锥,这个圆锥的体积是 cm3。
46.(2024六下·汝城期中)在一个比例里,两个内项互为倒数,一个外项是2.5,另一个外项是 。如果一个内项是0.5,那么这个比例可能是 。
47.(2024六下·雷州期中)一个长为 2mm 的精密零件,画在图纸上为6cm,这幅图的比例尺为 。
48.(2024六下·汝城期中)一个长方形零件长3 mm、宽2 mm,李工程师把它画在图纸上,量得零件长6cm,这幅图的比例尺是 ,图中零件的宽是 cm。
49.(2024六下·雷州期中)如果=y(x/y≠0)那么:y= : 。
50.(2023六下·怀来期中)小红到书店买5本同样的书,收银员只收了4本书的钱,这些书相当于打 折销售,最终小红少付了10元钱,若不打折小红应付 元。
答案解析部分
1.4:3=8:6(答案不唯一)
解:根据4×6=3×8,写成一个比例式是4:3=8:6(答案不唯一);
故答案为:4:3=8:6(答案不唯一)。
根据比例的基本性质:内项积等于外项积,可以将等式写成比例的形式(答案不唯一)。
2.八;640
解:200÷(200+50)
=200÷250
=80%
=八折
800×80%=640(元)
故答案为:八,640。
先用加法求出原价,用现价除以原价即可得出现价是原价的百分之几,即打的折数;用原价乘上折数就是现价。
3.54
解:18×3=54(平方厘米);
故答案为:54。
等底等高的圆锥体积是圆柱体积的,因此,如果圆柱和圆锥的体积相等,高也相等,那么圆锥的底面积就是圆柱底面积的3倍,据此解答。
4.600
解:60÷π=(cm),
80÷2÷
=40÷
=π
(÷2)2×π×π
=×π×π
=900×
=600(cm3)
故答案为:600。
圆柱的底面直径=底面周长÷π,那么圆柱的高=增加的表面积÷2÷底面直径,所以圆柱的体积=(底面直径÷2)2×π×高,据此代入数值作答即可。
5.1:4000000;2
解:1厘米:40千米
=1厘米:4000000厘米
=1:4000000;
80千米=8000000厘米
8000000×=2(厘米);
故答案为:1:4000000;2。
由线段比例尺可知,图上1厘米表示实际距离40千米,再根据比例尺=图上距离:实际距离,代入数值计算即可改写成数值比例尺;再根据图上距离=实际距离×比例尺,代入数值计算即可。
6.301.44
解:增加的表面积是长方体的左右两个面,面积是底面半径×高,
48÷2=24(平方厘米)
24÷4=6(厘米)
3.14×4×4×6=50.24×6=301.44(立方厘米)
故答案为:301.44。
增加的表面积÷2=增加的1个面的面积,增加的1个面的面积÷圆柱的底面半径=圆柱的高,
π×底面半径的平方×高=圆柱的体积。
7.50.24
解:12.56×4=50.24(平方厘米);
故答案为:50.24。
圆柱的侧面积=底面周长×高,据此代入数值计算即可。
8.2:3;84
解:1-42%-30%=28%,28%:42%=2:3;
126÷42%=300(人),300×28%=84(人)。
故答案为:2:3;84。
把参与检测的人数看作单位“1”,1-假性近视的人数占的百分比-视力正常的人数占的百分比=近视人数占的百分比,近视人数:视力正常人数=近视人数占的百分比:视力正常的人数占的百分比;六年级视力正常人数÷视力正常人数占的百分比=参与检测人数,参与检测人数×近视人数占的百分比=近视人数。
9.1.5
解:设水塔高x米。
x:22.5=3:45
45x=22.5×3
45x=67.5
x=67.5÷15
x=1.5
水塔高1.5米。
故答案为:1.5。
水塔高:水塔影长=标杆高:标杆的影长,据此列比例,根据比例的基本性质解比例。
10.9;24
解:6×3×4=72(立方厘米)
72÷8=9(平方厘米)
72×3÷9
=216÷9
=24(厘米)
故答案为:9;24。
根据题意,长方体的体积等于圆柱的体积,用体积除以高即可求出圆柱的底面积;再用体积乘3,再除以底面积,即可求出圆锥的高。
11.(1)正
(2)3.6
解:(1)30÷6=5
250÷50=5
它们的比值一定,所以a和b成正比例。
(2)30×6÷50
=180÷50
=3.6
当m=3.6时, a和b成反比例 。
故答案为:(1)正;(2)3.6。
(1) 如果a、b成正比例,那么a与b的比值一定 ;据此先计算再判断。
(2)a和b成反比例 ,就是a和b的乘积一定;先用a乘b求出积,再用这个积除以50即可。
12.-12;+24
解:日均最高气温是零下12℃,可记作-12℃,最高气温是24℃,可记作+24℃。
故答案为:-12;+24。
零上气温记作正,则零下气温就记作负。
13.226.08;251.2
解:8÷2=4(厘米)
侧面积:3.14×8×5
=25.12×5
=125.6(平方厘米)
底面积:3.14×42=50.24(平方厘米)
表面积:125.6+50.24×2
=125.6+100.48
=226.08(平方厘米);
50.24×5=251.2(立方厘米)。
故答案为:226.08;251.2。
圆柱的侧面积=πdh,圆柱的底面积=πr2,圆柱的表面积=侧面积+底面积×2;圆柱的体积=底面积×高。
14.成正;不成;不成
解:圆的周长=π×圆的直径,所以圆的周长与直径成正比例,如果圆的周长一定,它的直径和圆周率不成比例,如果圆的直径一定,它的周长和周周率不成比例。
故答案为:成正;不成;不成。
已知y=kx(x,y≠0),当k一定时,x和y成正比例。
15.图上;实际
一幅平面图上的比例尺是50:1,表示图上距离是实际距离的50倍。
故答案为:图上;实际。
图上距离:实际距离=比例尺。为了计算方便,一般把比例尺写成前项或后项是1的形式。
16.+2500元;-3800元
解:理财收入2500元,记作+2500元,
支出费用3800元, 记作-3800元。
故答案为:+2500元;-3800元。
收入用正数表示,支出用负数表示。
17.5
解:4÷=5,所以另一个外项是5。
故答案为:5。
在比例中,两个外项的积等于两个内项的积;
最小的合数是4。
18.31.4;5
解:1570÷50=31.4(cm);
31.4÷2÷3.14
=15.7÷3.14
=5(cm);
故答案为:31.4;5。
根据圆柱的侧面积=底面周长×高,据此可求出底面周长,再根据圆的周长=2×π×r,据此可求出底面的半径。
19.14.4;4.8
解:9.6÷(3-1)
=9.6÷2
=4.8(立方厘米)
圆柱的体积:4.8×3=14.4(立方厘米)
圆锥的体积:4.8×1=4.8(立方厘米)
故答案为:14.4;4.8。
根据等底等高的圆柱的体积是圆锥体积的3倍可知:圆柱的体积占3份,圆锥的体积占1份,则两者的体积差占(3-1)份。两者的体积差÷(3-1)=一份的体积,一份的体积×圆柱的体积占的份数=圆柱的体积,一份的体积×圆锥的体积占的份数=圆锥的体积。
20.9;16;75;七五;七成五
解:3÷4==;
3÷4==;
3÷4=0.75=75%;
3÷4=75%=七五折=七成五;
所以3÷4===75%=七五折=七成五。
故答案为:9;16;75;七五;七成五。
小数化成百分数,把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折,即几成。
21.250;8
解:(10+15)÷(90%-80%)
=25÷10%
=250(元);
250×80%+10
=200+10
=210(元);
218-210=8(元);
故答案为:250;8。
打八折出亏10元,打九折赚15元,是把标价看作单位“1”,标价的80%与标价的90%相差(10+15)元,因此,用(10+15)除以(90%-80%)即可求出标价;再用标价乘80%加10求出进价,最后用标价减去进价就是赚的钱;据此解答。
22.9
解:(1)28.26÷3.14÷2=4.5(厘米)
3.14×4.52×15.7
=63.585×15.7
=998.2645(平方厘米)
(2)15.7÷3.14÷2=2.5(厘米)
3.14×2.52×28.26
=19.625×28.26
=554.6025(平方厘米)
因为998.2645>554.6025
所以直径是:4.5×2=9(厘米)
故答案为:9。
先以28.26厘米为圆柱形的底面周长,15.7厘米为圆柱形的高,求出圆柱形的体积;再以15.7厘米为圆柱形的底面周长,28.26厘米为圆柱形的高,求出圆柱形的体积。再比较两个体积的大小即可。
23.25;16
解:如果x和y成正比例,a=20÷4×5=25;
如果x和y成反比例,a=4×20÷5=16。
故答案为:25;16。
当两个量成正比例关系时,这两个量的比值一定;
当两个量成反比例关系时,这两个量的乘积一定。
24.,
解:4÷4=1;
故答案为:1。
比例的基本性质是:内项积等于外项积,因此,两个内项积是最小的合数,那么两个外项的积也是最小的合数,最小的合数是4,用4除以已知的外项,即可求出另一个外项。
25.502.4
解:12.56×2÷3.14÷2
=25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×42×10
=50.24×10
=502.4(立方厘米)。
故答案为:502.4。
这个圆柱的体积=底面积×高=π×半径2×高;其中,半径=长方体的长×2÷π÷2。
26.;;正
解:如果,那么x:y=:;
x:y=:=÷=(一定),比值一定,所以x和y成正比例;
故答案为:;;正。
根据比例的基本性质:内项积等于外项积,可以将等式写成比例的形式;再根据正、反比例的意义(两种相关联的量,一种量变化,另一种量随之变化,如果它们的比值一定,则这两种量成正比例关系,如果它们的乘积一定,则这两种量成反比例关系)判断x和y组成的是什么比例。
27.280
解:1400-1400×80%
=1400-1120
=280(元)
故答案为:280。
根据现价=原价×折扣,求出现价,再用原价减去现价,即可求出便宜的钱数。
28.188.4
解:半径:60÷2÷15
=30÷15
=2(厘米);
体积:3.14×22×15
=3.14×4×15
=188.4(立方厘米);
故答案为:188.4。
拼成的长方体比圆柱多了2个长为圆柱半径,宽为圆柱的高的长方形面积,因此,用增加的面积除以2再除以圆柱的高可以求出圆柱的半径,再根据圆柱体积=π×半径2×高,代入数值计算即可。
29.1
解:A×B=C可以化为A×B=C×1,
由A×B=C×1可得:A:C=1:B。
故答案为:1。
在A×B=C×1中,根据比例的外项之积等于比例的内项之积。把A×B看做比例的外项,C×1看做比例的內项,据此把反比例改写成正比例的形式。
30.圆锥;50.24
解:以直角三角形的一条直角边为轴旋转一周可以得到一个圆锥;
①半径是3厘米,高是4厘米,
3.14×32×4×
=3.14×3×4
=37.68(立方厘米)
②半径是4厘米,高是3厘米,
3.14×42×3×
=3.14×16
=50.24(立方厘米);
50.24>37.68,所以它的体积最大是50.24立方厘米。
故答案为:圆锥;50.24。
以直角三角形的一条直角边为轴旋转一周可以得到一个圆锥,旋转得到的圆锥有两种,①半径是3厘米,高是4厘米;②半径是4厘米,高是3厘米;根据圆锥体积=π×半径2×高×,代入数值分别计算出两个圆锥的体积,再比较选出体积最大的即可。
31.31.4
解:3.14×2×10×50
=6.28×10×50
=62.8×50
=3140(平方厘米)=31.4平方分米;
故答案为:31.4。
做圆柱形烟囱需要的铁皮面积是圆柱的侧面积,根据圆柱侧面积=圆周长×高,据此代入数值计算,最后再进行单位换算即可。
32.50.24;37.68
解:需要的铁皮面积:3.14×22+3.14×2×2×3
=12.56+12.56×3
=12.56+37.68
=50.24(dm2);
最多可以装水体积:3.14×22×3
=12.56×3
=37.68(dm3);
故答案为:50.24;37.68。
需要的铁皮面积=底面积+侧面积=π×半径2+底面周长×高,最多可以装水的体积=圆柱的体积=π×半径2×高;据此代入数值计算即可。
33.1874;6280
解:表面积:3.14×(20÷2)2×2+3.14×20×20
=3.14×100×2+1256
=618+1256
=1874(平方厘米);
体积:3.14×(20÷2)2×20
=3.14×100×20
=6280(立方厘米);
故答案为:1874;6280。
由题意可知,这个圆柱的底面直径与高都是20厘米,根据圆柱表面积=底面积×2+侧面积,侧面积=底面周长×高,体积=底面积×高,代入数值计算即可。
34.80;100.48
解:8×5×2
=40×2
=80(平方厘米)
3.14×(8÷2)2×2
=3.14×16×2
=50.24×2
=100.48(平方厘米)
故答案为:80;100.48。
根据题意,把一个圆柱沿底面直径切割成两个半圆柱,那么增加的表面积是2个切面的面积,切面是长方形,宽等于圆柱的高5cm,长等于圆柱的底面直径8cm,根据长方形的面积公式S=ab,求出一个切面的面积,再乘2,即是增加的表面积; 沿平行于底面横切成两个圆柱,那么增加的表面积是2个切面的面积,切面是圆形,圆柱的底面直径8cm,根据圆形的面积公式S=πr2,求出一个切面的面积,再乘2,即是增加的表面积。
35.120
解:6×10×2
=60×2
=120(平方分米);
故答案为:120。
沿底面直径锯成两块,增加的是两个长为底面直径,宽为高的长方形面积,据此解答。
36.6.28
解:3.14×4=12.56(厘米),所以圆柱的底面周长是12.56厘米,高是6.28厘米。
故答案为:6.28。
圆柱的底面周长和高分别是展开图的长和宽,根据底面直径求出底面周长,也就是长方形的长,那么长方形另一条边就是圆柱的高。
37.24
解:因为斜边最长,所以3cm、4cm是直角三角形的两条直角边,
长度按2:1放大,直角三角形的两条直角边是6cm、8cm,
6×8÷2=24(平方厘米),放大后的三角形的面积是24平方厘米。
故答案为:24。
直角三角形的面积=两条直角边的积÷2。
38.113.04;138.16;37.68
解:圆柱的侧面积:3.14×2×2×9
=3.14×4×9
=12.56×9
=113.04(平方厘米);
圆柱的表面积:3.14×22×2+113.04
=3.14×4×2+113.04
=25.12+113.04
=138.16(平方厘米);
圆柱的体积:3.14×22×9
=3.14×4×9
=113.04(立方厘米);
圆锥的体积:113.04×=37.68(立方厘米);
故答案为:113.04;138.16;37.68。
根据圆柱的侧面积=底面周长×高,圆柱的表面积=底面积×2+侧面积,圆柱的体积=底面积×高,代入数值计算即可;与圆柱等底等高的圆锥的体积是它体积的,再用圆柱的体积乘即可求出圆锥的体积。
39.整圆;大小不同的扇形
解:扇形统计图是用整圆表示总数,用大小不同的扇形表示各部分所占总数的百分比。
故答案为:整圆;大小不同的扇形。
扇形统计图是用整圆表示总数,用大小不同的扇形表示各部分所占总数的百分比。
40.600
解: 10÷=60000000(厘米)
60000000厘米=600(千米)
故答案为:600。
根据“图上距离÷比例尺=实际距离”,代入数值,计算即可。
41.12
解:2.4×3÷0.6
=7.2÷0.6
=12(分米)。
故答案为:12。
圆锥的体积=底面积×高×,因此,圆锥的高=圆锥体积×3÷底面积。
42.753.6立方分米
解:3.14×(2÷2)2×4×60
=3.14×4×60
=12.56×60
=753.6(立方分米);
故答案为:753.6立方分米。
每秒流过的油的体积,就是直径为2分米,高为4分米的圆柱的体积,圆柱的体积=,1分钟=60秒,相当于60个这样的圆柱,据此解答。
43.85;10
解:现价是原价的85%,
1-90%=10%;
故答案为:85;10。
门票八五折优惠,也就是按原价的85%出售,因此现价是原价的85%,九折就是90%,学习用品一律打九折出售,就是按原价的90%出售,即比原价便宜了1-90%=10%,据此即可求解。
44.188.4
解:设正方体的棱长是a厘米,正方体的棱长也是圆柱的底面直径,正方体的高也是圆柱的高,
圆柱的底面半径:a÷2=a(厘米),
圆柱的体积:π×a×a×a=π××a×a×a=π××240=60π=188.4(立方厘米)
故答案为:188.4。
π×底面半径的平方×高=圆柱的体积,据此解答。
45.113.04
解:当以3cm的边为轴时,圆锥的体积:62×3.14×3×=113.04(cm3);
当以6cm的边为轴时,圆锥的体积:32×3.14×6×=56.52(cm3)。
113.04>56.52,所以这个圆锥的体积是113.04cm3。
故答案为:113.04。
圆锥的体积=πr2h×,据此代入数值作答即可。
46.0.4;2.5:0.5=2:0.4
解:两个内项互为倒数,两个内项的积是1,
1÷2.5=0.4,另一个外项是0.4,
1÷0.5=2,如果一个内项是0.5,那么这个比例可能是2.5:0.5=2:0.4。
故答案为:0.4;2.5:0.5=2:0.4。
第一空:比例的两个内项之积÷其中一个外项=另一个外项;
第二空:比值相等的两个比,可以组成比例。
47.30:1
解:6cm=60mm,60mm:2mm=30:1,所以这幅图的比例尺为30:1。
故答案为:30:1。
先把单位进行换算,即6cm=60mm,那么这幅图的比例尺=图上距离:实际距离。
48.20:1;4
解:6cm:3mm
=60mm:3mm
=60:3
=(60÷3):(3÷3)
=20:1
2×=40(mm)=4(cm)
故答案为:20:1;4。
根据比例尺的意义可知,比例尺=图上距离:实际距离,图上距离=实际距离×比例尺,据此代入数据解答即可。
49.9;8
解:x:y=:=9:8。
故答案为:9;8。
在比例中,两个外项的积等于两个内项的积,据此作答即可。
50.八;50
解:4÷5=80%,即书店是按八折销售的;
10×5=50元;
故答案为:八;50。
买了5本同样的书,收银员只收了4本书的钱,即收了原价的4÷5=80%,所以书店是按八折销售的;根据买5本书付了4本的钱,可知少付了一本书的钱,最终小明少付了10元,也就是说一本书10元钱,据此解答即可。
期中考试真题分类汇编12 填空题
一、填空题
1.(2024六下·徐闻期中)根据4×6=3×8,写成一个比例式是 。
2.(2024六下·汉川期中)某服装店一件休闲装现价200元,比原价少了50元,相当于打了 折。照这样的折扣,原价800元的西装,现价 元。
3.(2024六下·七星关期中)一个圆柱和一个圆锥的体积相等,高也相等,已知圆柱的底面积是18平方厘米,圆锥的底面积是 平方厘米。
4.(2024六下·雷州期中)把一个底面周长大约 60cm 的圆柱沿着直径垂直底面切成两个半圆柱,表面积增加了 80cm3,这个圆柱的体积是 cm3。
5.(2024六下·徐闻期中)一幅图的比例尺是,这个比例尺用数值比例尺表示为 ;A、B两地相距80km,画在这幅图上应是 cm。
6.(2024六下·黄石期中)将一个底面半径4厘米的圆柱切拼成一个近似的长方体(如下图),其表面积增加了48cm2,圆柱的体积是 立方厘米。
7.(2024六下·徐闻期中)一个圆柱体的底面周长是12.56cm,高4cm,它的侧面积是 cm2。
8.(2024六下·隆回期中)如图,本次视力检测中,近视人数与视力正常人数的最简整数比是 。如果本次视力检测中,六年级视力正常的共有126人,近视学生有 人。
9.(2024六下·汝城期中)测量小组测量水塔的高度,量得水塔影长是22.5m,同时同地量得附近一根3m 长的标杆的影长是45m,那么水塔高 m。
10.(2024六下·汉川期中)王红把下图中的长方体橡皮泥捏成一个高是8cm的圆柱,捏成的圆柱的底面积是 cm2.如果捏成与圆柱底面相等的圆锥,这个圆锥的高是 cm。
11.(2024六下·汉川期中)下表中a和b是两种相关联的量。
a 30 m
b 6 50
(1)当m=250时,a和b成 比例.
(2)当m= 时,a和b成反比例.
12.(2024六下·汉川期中)“一带一路”沿线国家之一俄罗斯,某月的日均最高气温是零下12℃,可记作 ℃.我国海南自贸区该月的日均最高气温是24℃,可记作 ℃.
13.(2024六下·隆回期中)一个圆柱的底面直径是8厘米,高是5厘米,它的表面积是 平方厘米,体积是 立方厘米。
14.(2024六下·雷州期中)圆的周长与直径 比例,如果圆的周长一定,它的直径和圆周率 比例,
如果圆的直径一定,它的周长和周周率 比例。(填“成正”、“成反”或“不成”)
15.(2024六下·汝城期中)一幅平面图上的比例尺是50:1,表示 距离是 距离的50倍。
16.(2024六下·汝城期中) 李阿姨10月份工资收入为5000元,记作+5000元, 理财收入2500元,记作 ; 而当月支出费用3800元, 记作 。
17.(2024六下·雷州期中)在一个比例里,两个内项的积为最小的合数,一个外项为,另一个外项是 。
18.(2024六下·岷县期中)一个圆柱的侧面积是1570cm2,高是50cm,它的底面周长是 cm,底面的半径是 cm。
19.(2024六下·隆回期中)一个圆锥和它等底等高的圆柱的体积相差9.6立方厘米,圆柱的体积是 立方厘米,圆锥的体积是 立方厘米。
20.(2024六下·汉川期中)3÷4= = = %= 折= (填成数)
21.(2024六下·齐河期中)一支钢笔,打八折卖出亏10元,打九折卖出赚15元,则这件商品的标价是 元,若卖18元,可赚 元。
22.(2024六下·汉川期中)有一块长28.26厘米、宽15.7厘米的长方形铁皮,应配上直径 厘米的圆形铁皮,可以做成一个容积最大的圆柱体。
23.(2024六下·雷州期中)在下表中,如果和y成正比例,a是 ,如果和y成反比例,a是 。
x 4 5
y 20 a
24.(2024六下·徐闻期中)在比例里,两个内项的积是最小的合数,一个外项是4,另一个外项是 。
25.(2023六下·惠来期中)如图,把圆柱切开,拼成一个近似的长方体,量得长方体的长是12.56cm,高是10cm,这个圆柱的体积是 立方厘米。
26.(2024六下·徐闻期中)如果,那么x:y= : ,x和y成 比例。
27.(2024六下·汝城期中)一件商品打八折销售,原价1400元,那么便宜了 元。
28.(2024六下·七星关期中)把一个高是15厘米的圆柱平均切成若干等份,如右图所示,拼成一个近似的长方体,如果拼成的长方体的表面积比圆柱增加了60平方厘米,原来圆柱的体积是 立方厘米。
29.(2024六下·汝城期中) 如果A×B=C(A、B均不为0), 那么A:C= :B。
30.(2024六下·七星关期中)一个直角三角形的两条直角边分别是3厘米和4厘米,如果以它的一条直角边为轴,旋转一周,可以得到一个 ,它的体积最大是 立方厘米。
31.(2024六下·七星关期中)做一节底面半径是10厘米、长是50厘米的圆柱形烟囱,至少需要 平方分米的铁皮。
32.(2024六下·徐闻期中)一个圆柱体水桶(无盖),已知底面半径是2分米,高为3分米,那么做一个这样的水桶至少需要铁皮 dm2,最多可以装水 dm3。
33.(2024六下·七星关期中)从正面观察一个圆柱,看到的形状是一个边长是20厘米的正方形,这个圆柱的表面积是 平方厘米,体积是 立方厘米。
34.(2024六下·汝城期中)将一个底面直径是8cm,高是5cm的圆柱切成两个完全相等的部分,沿直径垂直切下,表面积增加 cm2,沿平行于底面横切,表面积增加 cm2。
35.(2024六下·七星关期中)一根圆柱形木料,底面直径是6分米,高是10分米,沿底面直径把它锯成完全一样的两块,表面积增加了 平方分米。
36.(2024六下·七星关期中)把一个圆柱的表面展开得到一个长方形和两个圆,如右图(单位:厘米),这个圆柱的高是 厘米。
37.(2024六下·汝城期中)一个直角三角形三条边的长分别为3cm、4cm、5cm,如果把这个三角形各边的长度按2:1放大,放大后的三角形的面积是 cm2。
38.(2024六下·七星关期中)一个圆柱的底面半径是2厘米,高是9厘米,这个圆柱的侧面积是 平方厘米,表面积是 平方厘米,和它等底等高的圆锥的体积是 立方厘米。
39.(2024六下·七星关期中)扇形统计图是用 表示总数,用 分别表示各部分所占总数的百分比。
40.(2024六下·汉川期中)小天家在A城市,姥姥家在B城市,他在比例尺是1:6000000的地图上量得A城市到B城市的铁路长约10厘米,A城市到B城市的实际铁路长约是 千米.
41.(2024六下·七星关期中)一个圆锥的体积是2.4立方分米,底面积是0.6平方分米,高是 分米。
42.(2024六下·凉州期中)一根圆柱形输油管,内直径是2分米,油在管内的流速是每秒4分米,则一分钟流过的油是 .
43.(2024六下·凉州期中)“六一”期间游乐场门票八五折优惠,现价是原价的 %.儿童文具店所有学习用品一律打九折出售,可以节省 %.
44.(2024六下·黄石期中)如下图所示,正方体的体积是240立方厘米,把它削成一个最大的圆柱。圆柱体积是 立方厘米。
45.(2024六下·雷州期中)一个直角三角形的两条直角边分别为3cm和6cm,现在以其中一条直角边为轴旋转一周得到一个尽可能大的圆锥,这个圆锥的体积是 cm3。
46.(2024六下·汝城期中)在一个比例里,两个内项互为倒数,一个外项是2.5,另一个外项是 。如果一个内项是0.5,那么这个比例可能是 。
47.(2024六下·雷州期中)一个长为 2mm 的精密零件,画在图纸上为6cm,这幅图的比例尺为 。
48.(2024六下·汝城期中)一个长方形零件长3 mm、宽2 mm,李工程师把它画在图纸上,量得零件长6cm,这幅图的比例尺是 ,图中零件的宽是 cm。
49.(2024六下·雷州期中)如果=y(x/y≠0)那么:y= : 。
50.(2023六下·怀来期中)小红到书店买5本同样的书,收银员只收了4本书的钱,这些书相当于打 折销售,最终小红少付了10元钱,若不打折小红应付 元。
答案解析部分
1.4:3=8:6(答案不唯一)
解:根据4×6=3×8,写成一个比例式是4:3=8:6(答案不唯一);
故答案为:4:3=8:6(答案不唯一)。
根据比例的基本性质:内项积等于外项积,可以将等式写成比例的形式(答案不唯一)。
2.八;640
解:200÷(200+50)
=200÷250
=80%
=八折
800×80%=640(元)
故答案为:八,640。
先用加法求出原价,用现价除以原价即可得出现价是原价的百分之几,即打的折数;用原价乘上折数就是现价。
3.54
解:18×3=54(平方厘米);
故答案为:54。
等底等高的圆锥体积是圆柱体积的,因此,如果圆柱和圆锥的体积相等,高也相等,那么圆锥的底面积就是圆柱底面积的3倍,据此解答。
4.600
解:60÷π=(cm),
80÷2÷
=40÷
=π
(÷2)2×π×π
=×π×π
=900×
=600(cm3)
故答案为:600。
圆柱的底面直径=底面周长÷π,那么圆柱的高=增加的表面积÷2÷底面直径,所以圆柱的体积=(底面直径÷2)2×π×高,据此代入数值作答即可。
5.1:4000000;2
解:1厘米:40千米
=1厘米:4000000厘米
=1:4000000;
80千米=8000000厘米
8000000×=2(厘米);
故答案为:1:4000000;2。
由线段比例尺可知,图上1厘米表示实际距离40千米,再根据比例尺=图上距离:实际距离,代入数值计算即可改写成数值比例尺;再根据图上距离=实际距离×比例尺,代入数值计算即可。
6.301.44
解:增加的表面积是长方体的左右两个面,面积是底面半径×高,
48÷2=24(平方厘米)
24÷4=6(厘米)
3.14×4×4×6=50.24×6=301.44(立方厘米)
故答案为:301.44。
增加的表面积÷2=增加的1个面的面积,增加的1个面的面积÷圆柱的底面半径=圆柱的高,
π×底面半径的平方×高=圆柱的体积。
7.50.24
解:12.56×4=50.24(平方厘米);
故答案为:50.24。
圆柱的侧面积=底面周长×高,据此代入数值计算即可。
8.2:3;84
解:1-42%-30%=28%,28%:42%=2:3;
126÷42%=300(人),300×28%=84(人)。
故答案为:2:3;84。
把参与检测的人数看作单位“1”,1-假性近视的人数占的百分比-视力正常的人数占的百分比=近视人数占的百分比,近视人数:视力正常人数=近视人数占的百分比:视力正常的人数占的百分比;六年级视力正常人数÷视力正常人数占的百分比=参与检测人数,参与检测人数×近视人数占的百分比=近视人数。
9.1.5
解:设水塔高x米。
x:22.5=3:45
45x=22.5×3
45x=67.5
x=67.5÷15
x=1.5
水塔高1.5米。
故答案为:1.5。
水塔高:水塔影长=标杆高:标杆的影长,据此列比例,根据比例的基本性质解比例。
10.9;24
解:6×3×4=72(立方厘米)
72÷8=9(平方厘米)
72×3÷9
=216÷9
=24(厘米)
故答案为:9;24。
根据题意,长方体的体积等于圆柱的体积,用体积除以高即可求出圆柱的底面积;再用体积乘3,再除以底面积,即可求出圆锥的高。
11.(1)正
(2)3.6
解:(1)30÷6=5
250÷50=5
它们的比值一定,所以a和b成正比例。
(2)30×6÷50
=180÷50
=3.6
当m=3.6时, a和b成反比例 。
故答案为:(1)正;(2)3.6。
(1) 如果a、b成正比例,那么a与b的比值一定 ;据此先计算再判断。
(2)a和b成反比例 ,就是a和b的乘积一定;先用a乘b求出积,再用这个积除以50即可。
12.-12;+24
解:日均最高气温是零下12℃,可记作-12℃,最高气温是24℃,可记作+24℃。
故答案为:-12;+24。
零上气温记作正,则零下气温就记作负。
13.226.08;251.2
解:8÷2=4(厘米)
侧面积:3.14×8×5
=25.12×5
=125.6(平方厘米)
底面积:3.14×42=50.24(平方厘米)
表面积:125.6+50.24×2
=125.6+100.48
=226.08(平方厘米);
50.24×5=251.2(立方厘米)。
故答案为:226.08;251.2。
圆柱的侧面积=πdh,圆柱的底面积=πr2,圆柱的表面积=侧面积+底面积×2;圆柱的体积=底面积×高。
14.成正;不成;不成
解:圆的周长=π×圆的直径,所以圆的周长与直径成正比例,如果圆的周长一定,它的直径和圆周率不成比例,如果圆的直径一定,它的周长和周周率不成比例。
故答案为:成正;不成;不成。
已知y=kx(x,y≠0),当k一定时,x和y成正比例。
15.图上;实际
一幅平面图上的比例尺是50:1,表示图上距离是实际距离的50倍。
故答案为:图上;实际。
图上距离:实际距离=比例尺。为了计算方便,一般把比例尺写成前项或后项是1的形式。
16.+2500元;-3800元
解:理财收入2500元,记作+2500元,
支出费用3800元, 记作-3800元。
故答案为:+2500元;-3800元。
收入用正数表示,支出用负数表示。
17.5
解:4÷=5,所以另一个外项是5。
故答案为:5。
在比例中,两个外项的积等于两个内项的积;
最小的合数是4。
18.31.4;5
解:1570÷50=31.4(cm);
31.4÷2÷3.14
=15.7÷3.14
=5(cm);
故答案为:31.4;5。
根据圆柱的侧面积=底面周长×高,据此可求出底面周长,再根据圆的周长=2×π×r,据此可求出底面的半径。
19.14.4;4.8
解:9.6÷(3-1)
=9.6÷2
=4.8(立方厘米)
圆柱的体积:4.8×3=14.4(立方厘米)
圆锥的体积:4.8×1=4.8(立方厘米)
故答案为:14.4;4.8。
根据等底等高的圆柱的体积是圆锥体积的3倍可知:圆柱的体积占3份,圆锥的体积占1份,则两者的体积差占(3-1)份。两者的体积差÷(3-1)=一份的体积,一份的体积×圆柱的体积占的份数=圆柱的体积,一份的体积×圆锥的体积占的份数=圆锥的体积。
20.9;16;75;七五;七成五
解:3÷4==;
3÷4==;
3÷4=0.75=75%;
3÷4=75%=七五折=七成五;
所以3÷4===75%=七五折=七成五。
故答案为:9;16;75;七五;七成五。
小数化成百分数,把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折,即几成。
21.250;8
解:(10+15)÷(90%-80%)
=25÷10%
=250(元);
250×80%+10
=200+10
=210(元);
218-210=8(元);
故答案为:250;8。
打八折出亏10元,打九折赚15元,是把标价看作单位“1”,标价的80%与标价的90%相差(10+15)元,因此,用(10+15)除以(90%-80%)即可求出标价;再用标价乘80%加10求出进价,最后用标价减去进价就是赚的钱;据此解答。
22.9
解:(1)28.26÷3.14÷2=4.5(厘米)
3.14×4.52×15.7
=63.585×15.7
=998.2645(平方厘米)
(2)15.7÷3.14÷2=2.5(厘米)
3.14×2.52×28.26
=19.625×28.26
=554.6025(平方厘米)
因为998.2645>554.6025
所以直径是:4.5×2=9(厘米)
故答案为:9。
先以28.26厘米为圆柱形的底面周长,15.7厘米为圆柱形的高,求出圆柱形的体积;再以15.7厘米为圆柱形的底面周长,28.26厘米为圆柱形的高,求出圆柱形的体积。再比较两个体积的大小即可。
23.25;16
解:如果x和y成正比例,a=20÷4×5=25;
如果x和y成反比例,a=4×20÷5=16。
故答案为:25;16。
当两个量成正比例关系时,这两个量的比值一定;
当两个量成反比例关系时,这两个量的乘积一定。
24.,
解:4÷4=1;
故答案为:1。
比例的基本性质是:内项积等于外项积,因此,两个内项积是最小的合数,那么两个外项的积也是最小的合数,最小的合数是4,用4除以已知的外项,即可求出另一个外项。
25.502.4
解:12.56×2÷3.14÷2
=25.12÷3.14÷2
=8÷2
=4(厘米)
3.14×42×10
=50.24×10
=502.4(立方厘米)。
故答案为:502.4。
这个圆柱的体积=底面积×高=π×半径2×高;其中,半径=长方体的长×2÷π÷2。
26.;;正
解:如果,那么x:y=:;
x:y=:=÷=(一定),比值一定,所以x和y成正比例;
故答案为:;;正。
根据比例的基本性质:内项积等于外项积,可以将等式写成比例的形式;再根据正、反比例的意义(两种相关联的量,一种量变化,另一种量随之变化,如果它们的比值一定,则这两种量成正比例关系,如果它们的乘积一定,则这两种量成反比例关系)判断x和y组成的是什么比例。
27.280
解:1400-1400×80%
=1400-1120
=280(元)
故答案为:280。
根据现价=原价×折扣,求出现价,再用原价减去现价,即可求出便宜的钱数。
28.188.4
解:半径:60÷2÷15
=30÷15
=2(厘米);
体积:3.14×22×15
=3.14×4×15
=188.4(立方厘米);
故答案为:188.4。
拼成的长方体比圆柱多了2个长为圆柱半径,宽为圆柱的高的长方形面积,因此,用增加的面积除以2再除以圆柱的高可以求出圆柱的半径,再根据圆柱体积=π×半径2×高,代入数值计算即可。
29.1
解:A×B=C可以化为A×B=C×1,
由A×B=C×1可得:A:C=1:B。
故答案为:1。
在A×B=C×1中,根据比例的外项之积等于比例的内项之积。把A×B看做比例的外项,C×1看做比例的內项,据此把反比例改写成正比例的形式。
30.圆锥;50.24
解:以直角三角形的一条直角边为轴旋转一周可以得到一个圆锥;
①半径是3厘米,高是4厘米,
3.14×32×4×
=3.14×3×4
=37.68(立方厘米)
②半径是4厘米,高是3厘米,
3.14×42×3×
=3.14×16
=50.24(立方厘米);
50.24>37.68,所以它的体积最大是50.24立方厘米。
故答案为:圆锥;50.24。
以直角三角形的一条直角边为轴旋转一周可以得到一个圆锥,旋转得到的圆锥有两种,①半径是3厘米,高是4厘米;②半径是4厘米,高是3厘米;根据圆锥体积=π×半径2×高×,代入数值分别计算出两个圆锥的体积,再比较选出体积最大的即可。
31.31.4
解:3.14×2×10×50
=6.28×10×50
=62.8×50
=3140(平方厘米)=31.4平方分米;
故答案为:31.4。
做圆柱形烟囱需要的铁皮面积是圆柱的侧面积,根据圆柱侧面积=圆周长×高,据此代入数值计算,最后再进行单位换算即可。
32.50.24;37.68
解:需要的铁皮面积:3.14×22+3.14×2×2×3
=12.56+12.56×3
=12.56+37.68
=50.24(dm2);
最多可以装水体积:3.14×22×3
=12.56×3
=37.68(dm3);
故答案为:50.24;37.68。
需要的铁皮面积=底面积+侧面积=π×半径2+底面周长×高,最多可以装水的体积=圆柱的体积=π×半径2×高;据此代入数值计算即可。
33.1874;6280
解:表面积:3.14×(20÷2)2×2+3.14×20×20
=3.14×100×2+1256
=618+1256
=1874(平方厘米);
体积:3.14×(20÷2)2×20
=3.14×100×20
=6280(立方厘米);
故答案为:1874;6280。
由题意可知,这个圆柱的底面直径与高都是20厘米,根据圆柱表面积=底面积×2+侧面积,侧面积=底面周长×高,体积=底面积×高,代入数值计算即可。
34.80;100.48
解:8×5×2
=40×2
=80(平方厘米)
3.14×(8÷2)2×2
=3.14×16×2
=50.24×2
=100.48(平方厘米)
故答案为:80;100.48。
根据题意,把一个圆柱沿底面直径切割成两个半圆柱,那么增加的表面积是2个切面的面积,切面是长方形,宽等于圆柱的高5cm,长等于圆柱的底面直径8cm,根据长方形的面积公式S=ab,求出一个切面的面积,再乘2,即是增加的表面积; 沿平行于底面横切成两个圆柱,那么增加的表面积是2个切面的面积,切面是圆形,圆柱的底面直径8cm,根据圆形的面积公式S=πr2,求出一个切面的面积,再乘2,即是增加的表面积。
35.120
解:6×10×2
=60×2
=120(平方分米);
故答案为:120。
沿底面直径锯成两块,增加的是两个长为底面直径,宽为高的长方形面积,据此解答。
36.6.28
解:3.14×4=12.56(厘米),所以圆柱的底面周长是12.56厘米,高是6.28厘米。
故答案为:6.28。
圆柱的底面周长和高分别是展开图的长和宽,根据底面直径求出底面周长,也就是长方形的长,那么长方形另一条边就是圆柱的高。
37.24
解:因为斜边最长,所以3cm、4cm是直角三角形的两条直角边,
长度按2:1放大,直角三角形的两条直角边是6cm、8cm,
6×8÷2=24(平方厘米),放大后的三角形的面积是24平方厘米。
故答案为:24。
直角三角形的面积=两条直角边的积÷2。
38.113.04;138.16;37.68
解:圆柱的侧面积:3.14×2×2×9
=3.14×4×9
=12.56×9
=113.04(平方厘米);
圆柱的表面积:3.14×22×2+113.04
=3.14×4×2+113.04
=25.12+113.04
=138.16(平方厘米);
圆柱的体积:3.14×22×9
=3.14×4×9
=113.04(立方厘米);
圆锥的体积:113.04×=37.68(立方厘米);
故答案为:113.04;138.16;37.68。
根据圆柱的侧面积=底面周长×高,圆柱的表面积=底面积×2+侧面积,圆柱的体积=底面积×高,代入数值计算即可;与圆柱等底等高的圆锥的体积是它体积的,再用圆柱的体积乘即可求出圆锥的体积。
39.整圆;大小不同的扇形
解:扇形统计图是用整圆表示总数,用大小不同的扇形表示各部分所占总数的百分比。
故答案为:整圆;大小不同的扇形。
扇形统计图是用整圆表示总数,用大小不同的扇形表示各部分所占总数的百分比。
40.600
解: 10÷=60000000(厘米)
60000000厘米=600(千米)
故答案为:600。
根据“图上距离÷比例尺=实际距离”,代入数值,计算即可。
41.12
解:2.4×3÷0.6
=7.2÷0.6
=12(分米)。
故答案为:12。
圆锥的体积=底面积×高×,因此,圆锥的高=圆锥体积×3÷底面积。
42.753.6立方分米
解:3.14×(2÷2)2×4×60
=3.14×4×60
=12.56×60
=753.6(立方分米);
故答案为:753.6立方分米。
每秒流过的油的体积,就是直径为2分米,高为4分米的圆柱的体积,圆柱的体积=,1分钟=60秒,相当于60个这样的圆柱,据此解答。
43.85;10
解:现价是原价的85%,
1-90%=10%;
故答案为:85;10。
门票八五折优惠,也就是按原价的85%出售,因此现价是原价的85%,九折就是90%,学习用品一律打九折出售,就是按原价的90%出售,即比原价便宜了1-90%=10%,据此即可求解。
44.188.4
解:设正方体的棱长是a厘米,正方体的棱长也是圆柱的底面直径,正方体的高也是圆柱的高,
圆柱的底面半径:a÷2=a(厘米),
圆柱的体积:π×a×a×a=π××a×a×a=π××240=60π=188.4(立方厘米)
故答案为:188.4。
π×底面半径的平方×高=圆柱的体积,据此解答。
45.113.04
解:当以3cm的边为轴时,圆锥的体积:62×3.14×3×=113.04(cm3);
当以6cm的边为轴时,圆锥的体积:32×3.14×6×=56.52(cm3)。
113.04>56.52,所以这个圆锥的体积是113.04cm3。
故答案为:113.04。
圆锥的体积=πr2h×,据此代入数值作答即可。
46.0.4;2.5:0.5=2:0.4
解:两个内项互为倒数,两个内项的积是1,
1÷2.5=0.4,另一个外项是0.4,
1÷0.5=2,如果一个内项是0.5,那么这个比例可能是2.5:0.5=2:0.4。
故答案为:0.4;2.5:0.5=2:0.4。
第一空:比例的两个内项之积÷其中一个外项=另一个外项;
第二空:比值相等的两个比,可以组成比例。
47.30:1
解:6cm=60mm,60mm:2mm=30:1,所以这幅图的比例尺为30:1。
故答案为:30:1。
先把单位进行换算,即6cm=60mm,那么这幅图的比例尺=图上距离:实际距离。
48.20:1;4
解:6cm:3mm
=60mm:3mm
=60:3
=(60÷3):(3÷3)
=20:1
2×=40(mm)=4(cm)
故答案为:20:1;4。
根据比例尺的意义可知,比例尺=图上距离:实际距离,图上距离=实际距离×比例尺,据此代入数据解答即可。
49.9;8
解:x:y=:=9:8。
故答案为:9;8。
在比例中,两个外项的积等于两个内项的积,据此作答即可。
50.八;50
解:4÷5=80%,即书店是按八折销售的;
10×5=50元;
故答案为:八;50。
买了5本同样的书,收银员只收了4本书的钱,即收了原价的4÷5=80%,所以书店是按八折销售的;根据买5本书付了4本的钱,可知少付了一本书的钱,最终小明少付了10元,也就是说一本书10元钱,据此解答即可。
同课章节目录
