期中考试真题分类汇编01 单选题(含答案+解析)---2024-2025学年苏教版四年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编01 单选题(含答案+解析)---2024-2025学年苏教版四年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 07:53:41 | ||
图片预览




文档简介
2024-2025学年苏教版四年级数学下册
期中考试真题分类汇编01 单选题
一、单选题
1.(2024四下·周村期中)甲地到乙地的高速公路全长1056千米,一辆货车以平均88千米/时的速度行驶,在求货车从甲地行驶到乙地需要多少小时时,计算如图所示。箭头所指的数表示的是( )
A.货车1小时行驶的路程 B.货车 12小时行驶的路程
C.货车2小时行驶的路程 D.货车10小时行驶的路程
2.(2023四下·冷水滩期中)下面各数中,要读出两个“零”的数是( )。
A.201008 B.300.06 C.805.07 D.190.07
3.(2023五上·巨野期中)如图,如果将△ABC向左平移2格,则顶点A’的位置用数对表示为( )。
A.(5,1) B.(1,1) C.(7,1) D.(3,3)
4.(2024四下·齐河期中)下面结果是用计算机算出来的,结果不合理的是( )
A.897÷3=299 B.345×26=8970 C.63129-3607=66736
5.(2024四下·白云期中)明明计算器上的数字“8”坏了,他要用这个计算器计算256×49,下面计算方法错误的是( )。
A.256×7×7 B.256×(50—1)
C.256×50—256 D.256×50—1
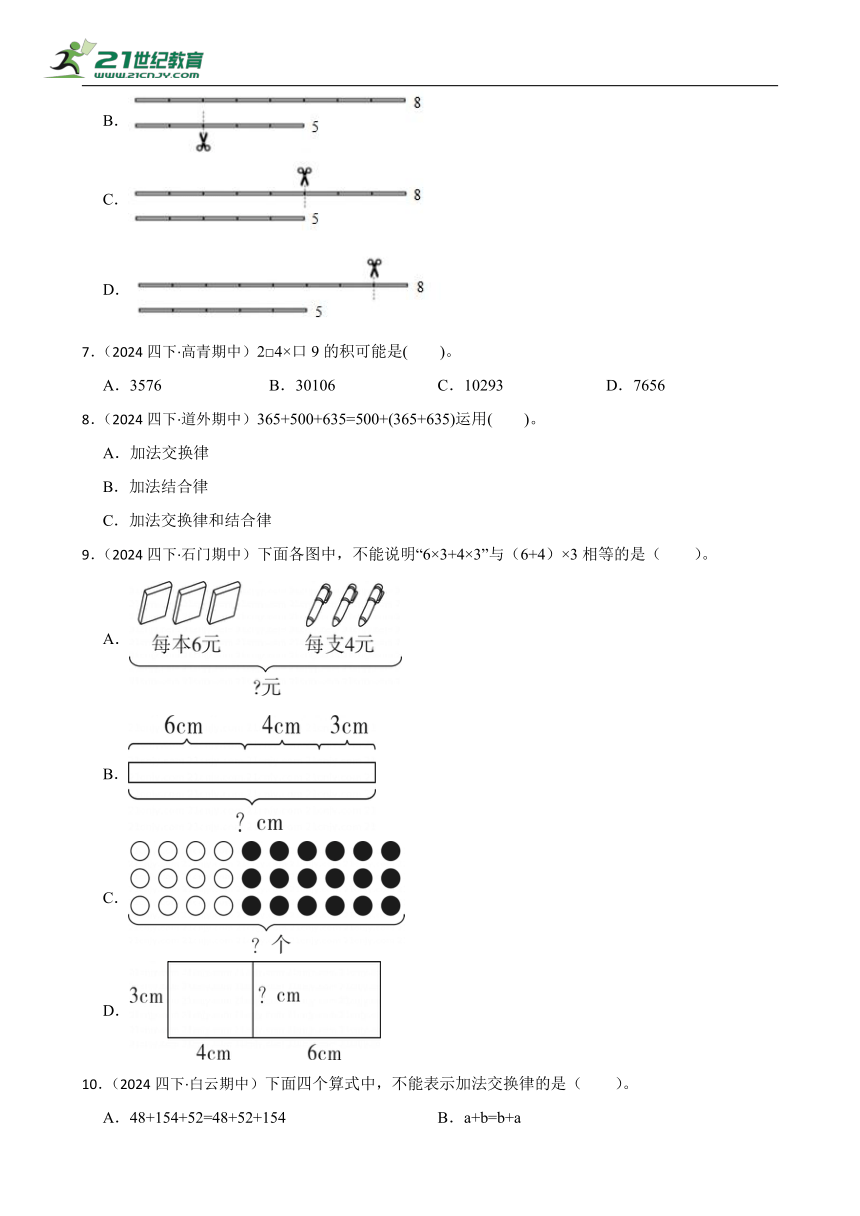
6.(2024四下·坊子期中) 淘气有两根塑料小棒,如下图所示。(单位:厘米)
他想剪断其中一根,把剪后的三根小棒首尾相接围一个三角形。以下四种剪法中,可以围成三角形的是( )。
A.
B.
C.
D.
7.(2024四下·高青期中)2□4×口9的积可能是( )。
A.3576 B.30106 C.10293 D.7656
8.(2024四下·道外期中)365+500+635=500+(365+635)运用( )。
A.加法交换律
B.加法结合律
C.加法交换律和结合律
9.(2024四下·石门期中)下面各图中,不能说明“6×3+4×3”与(6+4)×3相等的是( )。
A.
B.
C.
D.
10.(2024四下·白云期中)下面四个算式中,不能表示加法交换律的是( )。
A.48+154+52=48+52+154 B.a+b=b+a
C.甲+乙=乙+甲 D.49+76+151=59+141+76
11.(2024四下·孝昌期中)小亮在用计算器计算“48×256”时,按键“4”坏了,小亮想出了下列四种方法,其中错误的是( )。
A.50×256-2 B.(30+18)×256
C.(50-2)×256 D.16×3×256
12.(2024四下·海城期中)下列图中,不能说明“6×3 +4×3”与“(6 +4) ×3”相等的是( )。
A.
B.
C.
13.(2024四下·石门期中)已知在三角形ABC中,∠A+∠B=∠C,那么这是一个( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
14.(2024四下·湛江期中)下面每组三条线段,不能围成三角形的是( )。
A.3cm、4cm、5cm B.2cm、2cm、6cm C.3cm、3cm、3cm
15.(2024四下·齐河期中)在一个三角形中,有一个角是65°,另外两个角可能是( )
A.55°,70° B.95°,20° C.45°,80°
16.(2024四下·坊子期中)雷雷从七巧板中拿出了两个完全一样的直角三角形,拼成了一个大三角形,大三角形的内角和是( )。
A.90° B.180° C.270° D.360°
17.(2019四下·沾益期中)a×b的一个因数乘10,另一个因数也乘10,得到的积等于( ).
A.原来的积乘100 B.原来的积乘20 C.原来的积乘10
18.(2024四下·衡阳期中)计算时,小红使用的方法是:这是依据( )。
A.乘法结合律 B.加法结合律 C.乘法分配律
19.(2024四下·龙湖期中)下面可以用乘法分配律进行简便计算的算式是( )
A.(125+90)×8 B.52×25×4 C.7.6+1.25+2.4
20.(2024四下·高青期中)李明在课中研究三角形,用直尺、圆规绘制了下面三幅图,你知道他在探究什么问题吗 ( )
A.三角形的特征 B.三角形的内角和
C.三角形三边关系 D.三角形的周长
21.(2024四下·高青期中)下面四种事例中,没有应用平行四边形容易变形这一特点的是( )。
A.伸缩门 B.升降机 C.伸缩晾衣架 D.停车位
22.(2024四下·高青期中)如图,箭头所指的数大约是( )。
A.418000 B.455000 C.466000 D.520000
23.(2024四下·高青期中)李伯伯种植了14盆蝴蝶兰,以每盆135元的价格全部卖完,能卖多少元 用竖式计算李伯伯卖得的总钱数(如图),竖式中箭头所指的“135”表示( )。
A.1 盆蝴蝶兰卖了135元 B.10盆蝴蝶兰卖了1350元
C.4盆蝴蝶兰卖了135元 D.14盆蝴蝶兰卖了1350元
24.(2024四下·汝城期中)下列各数中,( )最接近5万。
A.5.01万 B.49999 C.51000
25.(2024四下·龙湖期中)下面图形中,属于轴对称图形的是( )。
A. B. C.
26.(2024四下·龙湖期中)与12×25计算结果不相等的算式是( )。
A.3×4×25 B.12×20+5 C.10×25+2×25
27.(2024四下·永兴期中)计算102×48,下面计算过程中没有运用乘法分配律的是( )。
A.100×48+2×48 B.102×40+102×8
C.102×50-102×2 D.102×6×8
28.(2024四下·湛江期中)算式56+72+28=56+(72+28)运用了( )。
A.加法交换律
B.加法结合律
C.加法交换律和结合律
29.(2024四下·上饶期中)下列( )组的得数不相等。
A.
B.
C.
30.(2024四下·丰县期中)2分)最接近30万的数是( )
A.298000 B.302000 C.300200 D.290800
31.(2024四下·游仙期中)小东把30×(□+4)算成了30×□+4,这样得到的结果与正确结果相比,( )。
A.少算了30 B.少算了29 C.少算了30×4 D.少算了29×4
32.(2024四下·龙湖期中) 一个三角形中,其中两个角的度数分别是40°和60°,那么第三个
角是( )。
A.80° B.60° C.40°
33.(2024四下·丰县期中)2分)下面的数中只读一个“零”的是( )
A.6606000 B.606600 C.6060600 D.600060
34.(2024四下·衡阳期中)299772km约是( )万千米(保留一位小数)。
A.30.0 B.29.0 C.29.9
35.(2024四下·孝昌期中)笔算17×21时,可以理解为( )。
A.1个17的和加上2个17的和 B.1个17的和加上2
C.1个17.的和加上20个17的和 D.2个17的和加上10个17的和
36.(2024四下·汝城期中)根据17×42=714, 下列计算错误的是 ( )
A.714÷17=42 B.42÷17= 714 C.42×17=714
37.(2024四下·丰县期中)2分)要使□21×31的积是五位数,□最小填( )
A.2 B.3 C.4 D.5
38.(2024四下·万载期中)下列说法完全正确的有( )个。
①把用“万”作单位的数改写成用“亿”作单位后,这个数会变大。
②4×(25×5)=25×4+5×4
③0.3和0.300的大小相等,但计数单位不同。
④(300-15)×(18-4),去掉括号后,结果不变。
A.1 B.2 C.3 D.4
39.(2024四下·齐河期中)若等腰三角形的其中两边长分别是5cm和11cm,则此三角形的周长是( )cm。
A.21 B.27 C.21或27
40.(2024四下·修水期中)下面计算与86×101结果相同的算式是( )
A.86×100+1 B.86×100﹣86 C.86×100+86
41.(2024四下·桑植期中)下面各数中,最接近20万的数是( )。
A.201000 B.199999 C.204000 D.200010
42.(2024四下·游仙期中)下面算式中,( )运用了乘法分配律。
A.42×(18+12)=42×30 B.a×b+a×c=a×(b+c)
C.4×a×5=a×(4×5) D.25×8×15=25×4×15×2
43.(2024四下·衡阳期中)如果▲×45=■×123(▲、■都不等于0),那么( )。
A.▲<■ B.▲=■ C.▲>■ D.无法确定
44.(2024四下·汝城期中)一个计算器的按键“4”坏了,如果用这个计算器计算125×24,那么下面方法正确的是( ) 。
A.125×8×3 B.125×25-1 C.125×25-25
45.(2024四下·安乡县期中)简算时,下面正确的方法是( ).
A.36×100-2 B.36×(100-2)
C.36×98+2 D.36×(98+2)
46.(2024四下·安乡县期中)看一本故事书,前两周每天看11页,后又看了9天,每天看14页,正好看完。这本书共有多少页 下面列式正确的是( )。
A.14×11-14×9 B.11×14+14×9
C.14×11×9 D.11+14×9
47.(2024四下·坊子期中)妈妈不小心把一块三角形玻璃摔成了三小块(如下图),现在要去重新配一块和原来一样大的玻璃,需要带编号为( )的玻璃。
A.① B.② C.③ D.①②
48.(2024四下·坊子期中)以平行四边形的一条边为底,能做出( )条高。
A.1 B.2 C.3 D.无数条
答案解析部分
1.D
解:88×10=880,箭头所指的数表示的是货车10小时行驶的路程 。
故答案为:D。
除数是两位数的除法:从被除数的高位除起,先看被除数的前两位,如果不够除,就多看一位;除到被除数的哪一位,就把商写在哪一位的上面,如果不够除,就在这一位上商0;每次除得的余数必须比除数小,并在余数右边一位落下被除数在这一位上的数,再继续除。
2.C
201008读作:二十万一千零八;
300.06读作:三百点零六;
805.07读作:八百零五点零七;
190.07读作:一百九十点零七。
故答案为:C。
整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零;
小数的读法:小数的整数部分就按整数的读法来读,小数部分就按数字的顺序依次读出来。
3.B
解:如果将△ABC向左平移2格,则顶点A’所对应的列为(3-2),所对应的行不变为1,即顶点A’的位置用数对表示为(1,1)。
故答案为:B。
点A向左平移2格后的点A’所对应的行不变,所对应的列为(3-2),据此解答即可。
4.C
解:A.299×3=897,所以897-3=299正确。
B.26×345=8970,所以345×26=8970正确。
C.63129-3607=59522,63129+3607=66736,所以63129-3607=66736的结果不合理。
故答案为:C。
A.用299×3来进行验算,看结果是不是等于897.
B.交换两个乘数的位置再计算一遍,看它们的结果是否相等。
C.63129<66736,可以发现被减数比差还小,按计算器时把减号错按成了加号。
5.D
解:256×7×7=256×(7×7)=256×49,A正确,
256×(50-1)=256×49,B正确,
256×50-256=256×50-256×1=256×(50-1)=256×49,C正确,
256×50-1≠256×49,D错误;
故答案为:D。
A.256×49中49接近7×7,可以将49写成7×7,用乘法结合律进行计算;B.256×49中49接近50,可以将49写成50-1,用乘法分配律进行计算;C.256×49中49接近50,可以将49写成50-1,用乘法分配律进行计算;D.根据四则运算法则,先算乘除,后算加减,有括号先算括号里的,据此解答。
6.C
解:根据三角形三边关系可知,应该剪长的那根小棒,因此,选项A和选项B错误;
选项C:5+3=8,8>5,所以可以围成三角形;
选项D:5+1=6,6<7,所以不可以围成三角形;
故答案为:C。
根据三角形的三边关系:两边之和大于第三边,进行解答。
7.D
解:2□4×口9的积末位数字是6,排除C;
假设□里面是最小的数0和1,204×19=3876,排除A;
假设□里面是最大的数9,294×99=29106,排除B;剩余D可能是这个积。
故答案为:D。
依据4×9=36的积末位数字是6,排除C;先假设□里面最小的数,最大数分别计算出积,用排除法得到答案。
8.C
解:365+500+635=500+(365+635)运用了加法交换律和加法结合律。
故答案为:C。
加法交换律:两个加数相加交换两个加数的位置,和不变,用字母表示为:a+b=b+a;
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变,用字母表示为:a+b+c=a+(b+c)。
9.B
解:根据图中表达的意思,只有B选项不能说明 “6×3+4×3”与(6+4)×3 ,它表示的是6+4+3的和。
故答案为:B
利用乘法分配律根据选项最终列式解答。
10.D
解:A.48+154+52=48+52+154,
B.a+b=b+a,
C.甲+乙=乙+甲,
D.49+76+151≠59+141+76;
故答案为:D。
根据加法交换律的定义,两个加数相加,交换加数的位置,和不变,49不等于59,数字改变和不同,据此解答即可。
11.A
解:48=50-2=30+18=16×3,所以BCD选项都正确;
48×256=(50-2)×256=50×256-2×256,所以A项错误。
故答案为:A。
因为按键“4”坏了,那么就把48替换成其他,而且要计算结果不变;据此作答即可。
12.A
解:A、6+4+3=13(cm),不能说明两算式相等,符合题意;
B、左边一行4个,有3行,右边一行有6个,有3行,所以一共有(6×3+4×3)个;也可以这样想:一行有(4+6)个,一共有3行,所以一共有(4+6)×3个,即6×3+4×3=(6+4)×3,能说明两算式相等,不符合题意;
C、小长方形面积=4×3,大长方形面积=6×3,组合图形面积=6×3+4×3;也可以先找组合图形的长(6+4)cm,宽3cm,则组合图形的面积=(6+4)×3,即6×3+4×3=(6+4)×3,能说明两算式相等,不符合题意。
故答案为:A。
A、看线段图可知是求三段线段一共长多少cm,即三段线段的和,不能说明题目中要求说明的两个算式相等;
B、看图可知是求一共有多少个小圆圈,方法一:右边每行个数×行数=右边小圆圈个数,左边每行个数×行数=左边小圆圈个数,右边每行个数×行数+左边每行个数×行数=小圆圈总数;方法二:右边每行个数+左边每行个数=总的每行个数,(右边每行个数+左边每行个数)×行数=小圆圈总数,方法一、二最后计算的都是小圆圈总数,所以右边每行个数×行数+左边每行个数×行数=(右边每行个数+左边每行个数)×行数,即可以说明两个算式相等;
C、长方形的面积=长×宽,先分别计算两个长方形的面积再求和即为组合图形的面积,或者先计算组合图形的长,再利用公式计算面积,两种方法都可以说明两个算式相等。
13.B
解:在三角形ABC中,∠A+∠B=∠C,
又因为三角形内角和是180°,所以∠A+∠B=∠C=90°,这是一个直角三角形。
故答案为:B。
有一个角是直角的三角形是直角三角形;据此解答。
14.B
解:A:任意两边之和大于第三边,能围成三角形;
B:, 不围成三角形 ;
C:任意两边之和大于第三边,能围成三角形;
故答案为:B。
三角形的三条边关系定则:任意两边之和大于第三边,任意两边之差小于第三边;据此求解即可。
15.B
解:180°-65°=115°
A:55°+70°=125°
B:95°+20°=115°
C:45°+80°=125°
故答案为:B。
根据三角形内角和等于180°,只要选项中的两个角的度数的和加上题干中已知角的度数,等于180°即可
16.B
解:所有三角形的内角和都是180°;
故答案为:B。
三角形的内角和是180°,据此解答。
17.A
10×10=100,得到的积等于原来的积乘100.
故答案为:A。
积扩大的倍数就是两个因数扩大的倍数之积。
18.C
解:21×101=21×(100+1)=21×100+21,这个算式是依据乘法分配律。
故答案为:C。
乘法分配律:ab+ac=a×(b+c),据此作答即可。
19.A
解:A:可以运用乘法分配律简便计算;
B:可以运用乘法结合律简便计算;
C:可以运用加法交换律简便计算。
故答案为:A。
乘法分配律:a×(b+c)=a×b+a×c;乘法结合律:a×b×c=a×(b×c);加法交换律:a+b=b+a。
20.C
解:他在探究三角形三边关系。
故答案为:C。
他在探究三角形三边关系,通过研究得出结论:三角形任意两边之和大于第三边,任意两边之差小于第三边。
21.D
解:停车位没有应用平行四边形容易变形这一特点,是为了停车方便才画成平行四边形。
故答案为:D。
平行四边形容易变形,其中,伸缩门、升降机、伸缩晾衣架等都应用了平行四边形容易变形这一特点 。
22.B
解:箭头所指的数大约在45万~46万之间,则可能是455000。
故答案为:B。
每个格表示2万,箭头所指的数大约在45万~46万之间,据此选择。
23.B
解:竖式中箭头所指的“135”表示:135×10=1350(元),即10盆蝴蝶兰卖了1350元。
故答案为:B。
两位数乘两位数的笔算乘法,相同数位对齐,先用第二个因数个位上的数去乘第一个因数,再用十位上去乘第一个因数,最后把两次乘得的积相加。
24.B
解:5万=50000
A:5.01万-5万=0.01万=100
B:50000-49999=1
C:51000-50000=1000
1最小,说明49999最接近5万。
故答案为:B。
哪个数与5万的差最小,哪个数就最接近5万。
25.C
解:不是轴对称图形,
不是轴对称图形,
是轴对称图形。
故答案为:C。
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。
26.B
解:A:3×4=12,所以3×4×25 =12×25;
B:12×20+12×5=12×(20+5)≠12×20+5;
C:10×25+2×25 =(10+2)×25=12×25;
故答案为:B。
乘法分配律:一个相同的数分别同两个不同的数相乘,积相加,等于这个相同的数乘另外两个不同数的和。
27.D
解:102×48=102×6×8应用了乘法结合律,其余各项应用乘法分配律。
故答案为:D。
乘法分配律:两个数的和与一个数相乘,等于这两个数分别与这个数相乘,再把所得的积相加;
乘法结合律:三个数相乘,可以先把前两个数相乘,再同第三个数相乘,或者先把后两个数相乘,再同第一个数相乘,结果不变。
28.B
29.C
解:根据乘法分配律可以判断,A组的得数相等;
根据乘法交换律、乘法结合律可以判断,B组的得数相等;
78×102=78×(100+2)=78×100+78×2,根据乘法分配律可以判断,C组的得数不相等。
故答案为:C。
乘法分配律:
一个数乘两个数的和,等于这个数分别同这两个数相乘,再把积相加,结果不变;
一个相同的数分别同两个不同的数相乘,积相减,等于这个相同的数乘另外两个不同数的差;
乘法交换律:两个数相乘,交换因数的位置,积不变;
乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
30.C
解:A:300000-298000=2000
B:302000-300000=2000
C:300200-300000=200
D:300000-290800 =9200
最接近30万的数是300200
故答案为:C。
哪个数与300000的差最小,说明哪个数最接近30万。
31.D
解:30×(□+4)-(30×□+4)
=30×□+30×4-30×□-4
=30×4-4
=29×4
故答案为:D。
根据乘法分配律,正确的结果为30×□+30×4,错误的计算结果为30×□-4,将正确的结果减去错误的结果即可。
32.A
解:180°-40°-60°=80°,第三个角是80°。
故答案为:A。
三角形的内角和-一个内角的度数-另一个内角的度数=第三个内角的度数。
33.D
解:A:6606000读作:六百六十万六千
B:606600读作:六十万六千六百
C:6060600 读作:六百零六万零六百
D:600060读作:六十万零六十
故答案为:D。
含有两级数的读法:先读万级,再读个级;万级的数,按照个级的读法来读,再在后面加一个万字;每级末尾不管有几个0都不读,其他数位上有一个0或连续几个0,都只读一个0。
34.A
解:299772千米=29.9772万千米≈30.0万千米。
故答案为:A。
把一个数取用“万”作单位的数,就是从这个数的末尾起数出四位点上小数点,再在后面加上“万”字;
把一个小数保留一位小数,就是把百分位上的数进行四舍五入即可。
35.C
解:17×21=17×(1+20)=17×1+17×20,可以理解为1个17的和加上20个17的和。
故答案为:C。
笔算两位数乘两位数,先用其中一个两位数的个位乘另一个两位数的每一位,所得结果的末尾与因数的个位对齐,然后用这个两位数的十位乘另一个两位数的每一位,所得结果的末尾与因数的十位对齐,最后把两次计算得出的结果加起来即可。
36.B
解:A:714÷17=42 ,正确,
B:42÷17= 714 ,错误,
C:42×17=714 ,正确。
故答案为:B。
积÷一个因数=另一个因数,据此可知A正确;两个数相乘,交换因数的位置,积不变,据此可知C正确。
37.C
解:321×31=9951,421×31=13051,
要使□21×31的积是五位数,□最小填4。
故答案为:C。
先计算,再根据计算的结果判断。
38.A
解:①把用“万”作单位的数改写成用“亿”作单位后,这个数不变,故错误;
②4×(25×5)=(25×4)×5,故错误;
③0.3和0.300的大小相等,但计数单位不同,0.3的计数单位是0.1,0.300的计数单位是0.01,故正确;
④(300-15)×(18-4),去掉括号后,结果变了,故错误。
故答案为:A。
改写前后的数大小不变;
乘法结合律:(a×b)×c=a×(b×c);
小数的末尾添上或去掉0,小数的大小不变;
一位小数的计数单位是0.1,三位小数的计数单位是0.001;
在有小括号的计算中,要先算小括号里面的,没有小括号的计算中,要按照先乘除后加减的计算方法计算。
39.B
解:当5cm为腰时,三边长为5、5、11,而5+5=10<11,此时无法构成三角形;
当5cm为底时,三边长为5、11、11,此时可以构成三角形,则它的周长是:5+11+11=27厘米。
故答案为:B。
三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边;
题目中没有明确腰和底,故要分情况讨论,再结合三角形的三边关系求解即可。
40.C
解:86×101
=86×(100+1)
=86×100+86×1
与86×101结果相同的算式是86×100+86
故答案为:C。
乘法分配律:一个数乘两个数的和,等于这个数分别同这两个数相乘,再把积相加,结果不变。
41.B
解:20万=200000
A:201000-200000=1000
B:200000-199999=1
C:204000-200000=4000
D:200010 -200000=10
最接近20万的数是199999
故答案为:B。
哪个数与20万的差最小,哪个数最接近20万。
42.B
解:乘法分配律公式为:a×(b+c)=a×b+a×c;
乘法分配律逆运算为:a×b+a×c=a×(b+c)。
故答案为:B。
乘法分配律:两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。
43.C
解:在▲×45=■×123中,45<123,所以▲>■。
故答案为:C。
在乘法计算中,一个乘数越小,另一个乘数就越大。
44.A
解:A:125×8×3 =125×(8×3)=125×24,
B:125×25-1≠ 125×24,
C:125×25-25 =25×(125-1)=124×25,
方法正确的是125×8×3 。
故答案为:A。
乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变;
乘法分配律:一个相同的数分别同两个不同的数相乘,积相减,等于这个相同的数乘另外两个不同数的差。
45.B
解:36×98
=36×(100-2)
=36×100-36×2。
故答案为:B。
计算36×98时,把98看作100-2,然后再乘36。
46.B
解:2×7=14(天),可以列成:11×14+14×9。
故答案为:B。
一周是7天,两周是7×2=14天,这本书的总页数=前两周平均每天看的页数×14天+后来平均每天看的页数×9天。
47.C
解:需要带编号为③的玻璃;
故答案为:C。
只带①和②无法确定玻璃的大小,而带③可以将两边延伸,确定玻璃的大小。
48.D
解:以平行四边形的一条边为底,能做出无数条高。
故答案为:D。
从平行四边形的底边向对边的一点引一条垂线,这点和垂足之间的距离就是平行四边形的高,据此解答。
期中考试真题分类汇编01 单选题
一、单选题
1.(2024四下·周村期中)甲地到乙地的高速公路全长1056千米,一辆货车以平均88千米/时的速度行驶,在求货车从甲地行驶到乙地需要多少小时时,计算如图所示。箭头所指的数表示的是( )
A.货车1小时行驶的路程 B.货车 12小时行驶的路程
C.货车2小时行驶的路程 D.货车10小时行驶的路程
2.(2023四下·冷水滩期中)下面各数中,要读出两个“零”的数是( )。
A.201008 B.300.06 C.805.07 D.190.07
3.(2023五上·巨野期中)如图,如果将△ABC向左平移2格,则顶点A’的位置用数对表示为( )。
A.(5,1) B.(1,1) C.(7,1) D.(3,3)
4.(2024四下·齐河期中)下面结果是用计算机算出来的,结果不合理的是( )
A.897÷3=299 B.345×26=8970 C.63129-3607=66736
5.(2024四下·白云期中)明明计算器上的数字“8”坏了,他要用这个计算器计算256×49,下面计算方法错误的是( )。
A.256×7×7 B.256×(50—1)
C.256×50—256 D.256×50—1
6.(2024四下·坊子期中) 淘气有两根塑料小棒,如下图所示。(单位:厘米)
他想剪断其中一根,把剪后的三根小棒首尾相接围一个三角形。以下四种剪法中,可以围成三角形的是( )。
A.
B.
C.
D.
7.(2024四下·高青期中)2□4×口9的积可能是( )。
A.3576 B.30106 C.10293 D.7656
8.(2024四下·道外期中)365+500+635=500+(365+635)运用( )。
A.加法交换律
B.加法结合律
C.加法交换律和结合律
9.(2024四下·石门期中)下面各图中,不能说明“6×3+4×3”与(6+4)×3相等的是( )。
A.
B.
C.
D.
10.(2024四下·白云期中)下面四个算式中,不能表示加法交换律的是( )。
A.48+154+52=48+52+154 B.a+b=b+a
C.甲+乙=乙+甲 D.49+76+151=59+141+76
11.(2024四下·孝昌期中)小亮在用计算器计算“48×256”时,按键“4”坏了,小亮想出了下列四种方法,其中错误的是( )。
A.50×256-2 B.(30+18)×256
C.(50-2)×256 D.16×3×256
12.(2024四下·海城期中)下列图中,不能说明“6×3 +4×3”与“(6 +4) ×3”相等的是( )。
A.
B.
C.
13.(2024四下·石门期中)已知在三角形ABC中,∠A+∠B=∠C,那么这是一个( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
14.(2024四下·湛江期中)下面每组三条线段,不能围成三角形的是( )。
A.3cm、4cm、5cm B.2cm、2cm、6cm C.3cm、3cm、3cm
15.(2024四下·齐河期中)在一个三角形中,有一个角是65°,另外两个角可能是( )
A.55°,70° B.95°,20° C.45°,80°
16.(2024四下·坊子期中)雷雷从七巧板中拿出了两个完全一样的直角三角形,拼成了一个大三角形,大三角形的内角和是( )。
A.90° B.180° C.270° D.360°
17.(2019四下·沾益期中)a×b的一个因数乘10,另一个因数也乘10,得到的积等于( ).
A.原来的积乘100 B.原来的积乘20 C.原来的积乘10
18.(2024四下·衡阳期中)计算时,小红使用的方法是:这是依据( )。
A.乘法结合律 B.加法结合律 C.乘法分配律
19.(2024四下·龙湖期中)下面可以用乘法分配律进行简便计算的算式是( )
A.(125+90)×8 B.52×25×4 C.7.6+1.25+2.4
20.(2024四下·高青期中)李明在课中研究三角形,用直尺、圆规绘制了下面三幅图,你知道他在探究什么问题吗 ( )
A.三角形的特征 B.三角形的内角和
C.三角形三边关系 D.三角形的周长
21.(2024四下·高青期中)下面四种事例中,没有应用平行四边形容易变形这一特点的是( )。
A.伸缩门 B.升降机 C.伸缩晾衣架 D.停车位
22.(2024四下·高青期中)如图,箭头所指的数大约是( )。
A.418000 B.455000 C.466000 D.520000
23.(2024四下·高青期中)李伯伯种植了14盆蝴蝶兰,以每盆135元的价格全部卖完,能卖多少元 用竖式计算李伯伯卖得的总钱数(如图),竖式中箭头所指的“135”表示( )。
A.1 盆蝴蝶兰卖了135元 B.10盆蝴蝶兰卖了1350元
C.4盆蝴蝶兰卖了135元 D.14盆蝴蝶兰卖了1350元
24.(2024四下·汝城期中)下列各数中,( )最接近5万。
A.5.01万 B.49999 C.51000
25.(2024四下·龙湖期中)下面图形中,属于轴对称图形的是( )。
A. B. C.
26.(2024四下·龙湖期中)与12×25计算结果不相等的算式是( )。
A.3×4×25 B.12×20+5 C.10×25+2×25
27.(2024四下·永兴期中)计算102×48,下面计算过程中没有运用乘法分配律的是( )。
A.100×48+2×48 B.102×40+102×8
C.102×50-102×2 D.102×6×8
28.(2024四下·湛江期中)算式56+72+28=56+(72+28)运用了( )。
A.加法交换律
B.加法结合律
C.加法交换律和结合律
29.(2024四下·上饶期中)下列( )组的得数不相等。
A.
B.
C.
30.(2024四下·丰县期中)2分)最接近30万的数是( )
A.298000 B.302000 C.300200 D.290800
31.(2024四下·游仙期中)小东把30×(□+4)算成了30×□+4,这样得到的结果与正确结果相比,( )。
A.少算了30 B.少算了29 C.少算了30×4 D.少算了29×4
32.(2024四下·龙湖期中) 一个三角形中,其中两个角的度数分别是40°和60°,那么第三个
角是( )。
A.80° B.60° C.40°
33.(2024四下·丰县期中)2分)下面的数中只读一个“零”的是( )
A.6606000 B.606600 C.6060600 D.600060
34.(2024四下·衡阳期中)299772km约是( )万千米(保留一位小数)。
A.30.0 B.29.0 C.29.9
35.(2024四下·孝昌期中)笔算17×21时,可以理解为( )。
A.1个17的和加上2个17的和 B.1个17的和加上2
C.1个17.的和加上20个17的和 D.2个17的和加上10个17的和
36.(2024四下·汝城期中)根据17×42=714, 下列计算错误的是 ( )
A.714÷17=42 B.42÷17= 714 C.42×17=714
37.(2024四下·丰县期中)2分)要使□21×31的积是五位数,□最小填( )
A.2 B.3 C.4 D.5
38.(2024四下·万载期中)下列说法完全正确的有( )个。
①把用“万”作单位的数改写成用“亿”作单位后,这个数会变大。
②4×(25×5)=25×4+5×4
③0.3和0.300的大小相等,但计数单位不同。
④(300-15)×(18-4),去掉括号后,结果不变。
A.1 B.2 C.3 D.4
39.(2024四下·齐河期中)若等腰三角形的其中两边长分别是5cm和11cm,则此三角形的周长是( )cm。
A.21 B.27 C.21或27
40.(2024四下·修水期中)下面计算与86×101结果相同的算式是( )
A.86×100+1 B.86×100﹣86 C.86×100+86
41.(2024四下·桑植期中)下面各数中,最接近20万的数是( )。
A.201000 B.199999 C.204000 D.200010
42.(2024四下·游仙期中)下面算式中,( )运用了乘法分配律。
A.42×(18+12)=42×30 B.a×b+a×c=a×(b+c)
C.4×a×5=a×(4×5) D.25×8×15=25×4×15×2
43.(2024四下·衡阳期中)如果▲×45=■×123(▲、■都不等于0),那么( )。
A.▲<■ B.▲=■ C.▲>■ D.无法确定
44.(2024四下·汝城期中)一个计算器的按键“4”坏了,如果用这个计算器计算125×24,那么下面方法正确的是( ) 。
A.125×8×3 B.125×25-1 C.125×25-25
45.(2024四下·安乡县期中)简算时,下面正确的方法是( ).
A.36×100-2 B.36×(100-2)
C.36×98+2 D.36×(98+2)
46.(2024四下·安乡县期中)看一本故事书,前两周每天看11页,后又看了9天,每天看14页,正好看完。这本书共有多少页 下面列式正确的是( )。
A.14×11-14×9 B.11×14+14×9
C.14×11×9 D.11+14×9
47.(2024四下·坊子期中)妈妈不小心把一块三角形玻璃摔成了三小块(如下图),现在要去重新配一块和原来一样大的玻璃,需要带编号为( )的玻璃。
A.① B.② C.③ D.①②
48.(2024四下·坊子期中)以平行四边形的一条边为底,能做出( )条高。
A.1 B.2 C.3 D.无数条
答案解析部分
1.D
解:88×10=880,箭头所指的数表示的是货车10小时行驶的路程 。
故答案为:D。
除数是两位数的除法:从被除数的高位除起,先看被除数的前两位,如果不够除,就多看一位;除到被除数的哪一位,就把商写在哪一位的上面,如果不够除,就在这一位上商0;每次除得的余数必须比除数小,并在余数右边一位落下被除数在这一位上的数,再继续除。
2.C
201008读作:二十万一千零八;
300.06读作:三百点零六;
805.07读作:八百零五点零七;
190.07读作:一百九十点零七。
故答案为:C。
整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零;
小数的读法:小数的整数部分就按整数的读法来读,小数部分就按数字的顺序依次读出来。
3.B
解:如果将△ABC向左平移2格,则顶点A’所对应的列为(3-2),所对应的行不变为1,即顶点A’的位置用数对表示为(1,1)。
故答案为:B。
点A向左平移2格后的点A’所对应的行不变,所对应的列为(3-2),据此解答即可。
4.C
解:A.299×3=897,所以897-3=299正确。
B.26×345=8970,所以345×26=8970正确。
C.63129-3607=59522,63129+3607=66736,所以63129-3607=66736的结果不合理。
故答案为:C。
A.用299×3来进行验算,看结果是不是等于897.
B.交换两个乘数的位置再计算一遍,看它们的结果是否相等。
C.63129<66736,可以发现被减数比差还小,按计算器时把减号错按成了加号。
5.D
解:256×7×7=256×(7×7)=256×49,A正确,
256×(50-1)=256×49,B正确,
256×50-256=256×50-256×1=256×(50-1)=256×49,C正确,
256×50-1≠256×49,D错误;
故答案为:D。
A.256×49中49接近7×7,可以将49写成7×7,用乘法结合律进行计算;B.256×49中49接近50,可以将49写成50-1,用乘法分配律进行计算;C.256×49中49接近50,可以将49写成50-1,用乘法分配律进行计算;D.根据四则运算法则,先算乘除,后算加减,有括号先算括号里的,据此解答。
6.C
解:根据三角形三边关系可知,应该剪长的那根小棒,因此,选项A和选项B错误;
选项C:5+3=8,8>5,所以可以围成三角形;
选项D:5+1=6,6<7,所以不可以围成三角形;
故答案为:C。
根据三角形的三边关系:两边之和大于第三边,进行解答。
7.D
解:2□4×口9的积末位数字是6,排除C;
假设□里面是最小的数0和1,204×19=3876,排除A;
假设□里面是最大的数9,294×99=29106,排除B;剩余D可能是这个积。
故答案为:D。
依据4×9=36的积末位数字是6,排除C;先假设□里面最小的数,最大数分别计算出积,用排除法得到答案。
8.C
解:365+500+635=500+(365+635)运用了加法交换律和加法结合律。
故答案为:C。
加法交换律:两个加数相加交换两个加数的位置,和不变,用字母表示为:a+b=b+a;
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变,用字母表示为:a+b+c=a+(b+c)。
9.B
解:根据图中表达的意思,只有B选项不能说明 “6×3+4×3”与(6+4)×3 ,它表示的是6+4+3的和。
故答案为:B
利用乘法分配律根据选项最终列式解答。
10.D
解:A.48+154+52=48+52+154,
B.a+b=b+a,
C.甲+乙=乙+甲,
D.49+76+151≠59+141+76;
故答案为:D。
根据加法交换律的定义,两个加数相加,交换加数的位置,和不变,49不等于59,数字改变和不同,据此解答即可。
11.A
解:48=50-2=30+18=16×3,所以BCD选项都正确;
48×256=(50-2)×256=50×256-2×256,所以A项错误。
故答案为:A。
因为按键“4”坏了,那么就把48替换成其他,而且要计算结果不变;据此作答即可。
12.A
解:A、6+4+3=13(cm),不能说明两算式相等,符合题意;
B、左边一行4个,有3行,右边一行有6个,有3行,所以一共有(6×3+4×3)个;也可以这样想:一行有(4+6)个,一共有3行,所以一共有(4+6)×3个,即6×3+4×3=(6+4)×3,能说明两算式相等,不符合题意;
C、小长方形面积=4×3,大长方形面积=6×3,组合图形面积=6×3+4×3;也可以先找组合图形的长(6+4)cm,宽3cm,则组合图形的面积=(6+4)×3,即6×3+4×3=(6+4)×3,能说明两算式相等,不符合题意。
故答案为:A。
A、看线段图可知是求三段线段一共长多少cm,即三段线段的和,不能说明题目中要求说明的两个算式相等;
B、看图可知是求一共有多少个小圆圈,方法一:右边每行个数×行数=右边小圆圈个数,左边每行个数×行数=左边小圆圈个数,右边每行个数×行数+左边每行个数×行数=小圆圈总数;方法二:右边每行个数+左边每行个数=总的每行个数,(右边每行个数+左边每行个数)×行数=小圆圈总数,方法一、二最后计算的都是小圆圈总数,所以右边每行个数×行数+左边每行个数×行数=(右边每行个数+左边每行个数)×行数,即可以说明两个算式相等;
C、长方形的面积=长×宽,先分别计算两个长方形的面积再求和即为组合图形的面积,或者先计算组合图形的长,再利用公式计算面积,两种方法都可以说明两个算式相等。
13.B
解:在三角形ABC中,∠A+∠B=∠C,
又因为三角形内角和是180°,所以∠A+∠B=∠C=90°,这是一个直角三角形。
故答案为:B。
有一个角是直角的三角形是直角三角形;据此解答。
14.B
解:A:任意两边之和大于第三边,能围成三角形;
B:, 不围成三角形 ;
C:任意两边之和大于第三边,能围成三角形;
故答案为:B。
三角形的三条边关系定则:任意两边之和大于第三边,任意两边之差小于第三边;据此求解即可。
15.B
解:180°-65°=115°
A:55°+70°=125°
B:95°+20°=115°
C:45°+80°=125°
故答案为:B。
根据三角形内角和等于180°,只要选项中的两个角的度数的和加上题干中已知角的度数,等于180°即可
16.B
解:所有三角形的内角和都是180°;
故答案为:B。
三角形的内角和是180°,据此解答。
17.A
10×10=100,得到的积等于原来的积乘100.
故答案为:A。
积扩大的倍数就是两个因数扩大的倍数之积。
18.C
解:21×101=21×(100+1)=21×100+21,这个算式是依据乘法分配律。
故答案为:C。
乘法分配律:ab+ac=a×(b+c),据此作答即可。
19.A
解:A:可以运用乘法分配律简便计算;
B:可以运用乘法结合律简便计算;
C:可以运用加法交换律简便计算。
故答案为:A。
乘法分配律:a×(b+c)=a×b+a×c;乘法结合律:a×b×c=a×(b×c);加法交换律:a+b=b+a。
20.C
解:他在探究三角形三边关系。
故答案为:C。
他在探究三角形三边关系,通过研究得出结论:三角形任意两边之和大于第三边,任意两边之差小于第三边。
21.D
解:停车位没有应用平行四边形容易变形这一特点,是为了停车方便才画成平行四边形。
故答案为:D。
平行四边形容易变形,其中,伸缩门、升降机、伸缩晾衣架等都应用了平行四边形容易变形这一特点 。
22.B
解:箭头所指的数大约在45万~46万之间,则可能是455000。
故答案为:B。
每个格表示2万,箭头所指的数大约在45万~46万之间,据此选择。
23.B
解:竖式中箭头所指的“135”表示:135×10=1350(元),即10盆蝴蝶兰卖了1350元。
故答案为:B。
两位数乘两位数的笔算乘法,相同数位对齐,先用第二个因数个位上的数去乘第一个因数,再用十位上去乘第一个因数,最后把两次乘得的积相加。
24.B
解:5万=50000
A:5.01万-5万=0.01万=100
B:50000-49999=1
C:51000-50000=1000
1最小,说明49999最接近5万。
故答案为:B。
哪个数与5万的差最小,哪个数就最接近5万。
25.C
解:不是轴对称图形,
不是轴对称图形,
是轴对称图形。
故答案为:C。
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。
26.B
解:A:3×4=12,所以3×4×25 =12×25;
B:12×20+12×5=12×(20+5)≠12×20+5;
C:10×25+2×25 =(10+2)×25=12×25;
故答案为:B。
乘法分配律:一个相同的数分别同两个不同的数相乘,积相加,等于这个相同的数乘另外两个不同数的和。
27.D
解:102×48=102×6×8应用了乘法结合律,其余各项应用乘法分配律。
故答案为:D。
乘法分配律:两个数的和与一个数相乘,等于这两个数分别与这个数相乘,再把所得的积相加;
乘法结合律:三个数相乘,可以先把前两个数相乘,再同第三个数相乘,或者先把后两个数相乘,再同第一个数相乘,结果不变。
28.B
29.C
解:根据乘法分配律可以判断,A组的得数相等;
根据乘法交换律、乘法结合律可以判断,B组的得数相等;
78×102=78×(100+2)=78×100+78×2,根据乘法分配律可以判断,C组的得数不相等。
故答案为:C。
乘法分配律:
一个数乘两个数的和,等于这个数分别同这两个数相乘,再把积相加,结果不变;
一个相同的数分别同两个不同的数相乘,积相减,等于这个相同的数乘另外两个不同数的差;
乘法交换律:两个数相乘,交换因数的位置,积不变;
乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
30.C
解:A:300000-298000=2000
B:302000-300000=2000
C:300200-300000=200
D:300000-290800 =9200
最接近30万的数是300200
故答案为:C。
哪个数与300000的差最小,说明哪个数最接近30万。
31.D
解:30×(□+4)-(30×□+4)
=30×□+30×4-30×□-4
=30×4-4
=29×4
故答案为:D。
根据乘法分配律,正确的结果为30×□+30×4,错误的计算结果为30×□-4,将正确的结果减去错误的结果即可。
32.A
解:180°-40°-60°=80°,第三个角是80°。
故答案为:A。
三角形的内角和-一个内角的度数-另一个内角的度数=第三个内角的度数。
33.D
解:A:6606000读作:六百六十万六千
B:606600读作:六十万六千六百
C:6060600 读作:六百零六万零六百
D:600060读作:六十万零六十
故答案为:D。
含有两级数的读法:先读万级,再读个级;万级的数,按照个级的读法来读,再在后面加一个万字;每级末尾不管有几个0都不读,其他数位上有一个0或连续几个0,都只读一个0。
34.A
解:299772千米=29.9772万千米≈30.0万千米。
故答案为:A。
把一个数取用“万”作单位的数,就是从这个数的末尾起数出四位点上小数点,再在后面加上“万”字;
把一个小数保留一位小数,就是把百分位上的数进行四舍五入即可。
35.C
解:17×21=17×(1+20)=17×1+17×20,可以理解为1个17的和加上20个17的和。
故答案为:C。
笔算两位数乘两位数,先用其中一个两位数的个位乘另一个两位数的每一位,所得结果的末尾与因数的个位对齐,然后用这个两位数的十位乘另一个两位数的每一位,所得结果的末尾与因数的十位对齐,最后把两次计算得出的结果加起来即可。
36.B
解:A:714÷17=42 ,正确,
B:42÷17= 714 ,错误,
C:42×17=714 ,正确。
故答案为:B。
积÷一个因数=另一个因数,据此可知A正确;两个数相乘,交换因数的位置,积不变,据此可知C正确。
37.C
解:321×31=9951,421×31=13051,
要使□21×31的积是五位数,□最小填4。
故答案为:C。
先计算,再根据计算的结果判断。
38.A
解:①把用“万”作单位的数改写成用“亿”作单位后,这个数不变,故错误;
②4×(25×5)=(25×4)×5,故错误;
③0.3和0.300的大小相等,但计数单位不同,0.3的计数单位是0.1,0.300的计数单位是0.01,故正确;
④(300-15)×(18-4),去掉括号后,结果变了,故错误。
故答案为:A。
改写前后的数大小不变;
乘法结合律:(a×b)×c=a×(b×c);
小数的末尾添上或去掉0,小数的大小不变;
一位小数的计数单位是0.1,三位小数的计数单位是0.001;
在有小括号的计算中,要先算小括号里面的,没有小括号的计算中,要按照先乘除后加减的计算方法计算。
39.B
解:当5cm为腰时,三边长为5、5、11,而5+5=10<11,此时无法构成三角形;
当5cm为底时,三边长为5、11、11,此时可以构成三角形,则它的周长是:5+11+11=27厘米。
故答案为:B。
三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边;
题目中没有明确腰和底,故要分情况讨论,再结合三角形的三边关系求解即可。
40.C
解:86×101
=86×(100+1)
=86×100+86×1
与86×101结果相同的算式是86×100+86
故答案为:C。
乘法分配律:一个数乘两个数的和,等于这个数分别同这两个数相乘,再把积相加,结果不变。
41.B
解:20万=200000
A:201000-200000=1000
B:200000-199999=1
C:204000-200000=4000
D:200010 -200000=10
最接近20万的数是199999
故答案为:B。
哪个数与20万的差最小,哪个数最接近20万。
42.B
解:乘法分配律公式为:a×(b+c)=a×b+a×c;
乘法分配律逆运算为:a×b+a×c=a×(b+c)。
故答案为:B。
乘法分配律:两个数的和同一个数相乘,等于把两个加数分别同这个数相乘,再把两个积加起来,结果不变。
43.C
解:在▲×45=■×123中,45<123,所以▲>■。
故答案为:C。
在乘法计算中,一个乘数越小,另一个乘数就越大。
44.A
解:A:125×8×3 =125×(8×3)=125×24,
B:125×25-1≠ 125×24,
C:125×25-25 =25×(125-1)=124×25,
方法正确的是125×8×3 。
故答案为:A。
乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变;
乘法分配律:一个相同的数分别同两个不同的数相乘,积相减,等于这个相同的数乘另外两个不同数的差。
45.B
解:36×98
=36×(100-2)
=36×100-36×2。
故答案为:B。
计算36×98时,把98看作100-2,然后再乘36。
46.B
解:2×7=14(天),可以列成:11×14+14×9。
故答案为:B。
一周是7天,两周是7×2=14天,这本书的总页数=前两周平均每天看的页数×14天+后来平均每天看的页数×9天。
47.C
解:需要带编号为③的玻璃;
故答案为:C。
只带①和②无法确定玻璃的大小,而带③可以将两边延伸,确定玻璃的大小。
48.D
解:以平行四边形的一条边为底,能做出无数条高。
故答案为:D。
从平行四边形的底边向对边的一点引一条垂线,这点和垂足之间的距离就是平行四边形的高,据此解答。
同课章节目录
