2025年北京朝阳高三2月六校联考数学(含答案)
文档属性
| 名称 | 2025年北京朝阳高三2月六校联考数学(含答案) |  | |
| 格式 | |||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 10:25:11 | ||
图片预览




文档简介
2025北京朝阳高三 2月六校联考
数 学
2025.2
第一部分(选择题 共 40 分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合 A = x x 3, x Z , B = x x2 1 ,则 A B =
(A) 1,0,1 (B) 3, 2,2,3 (C) 2,0,2 (D) 2,2
2i
(2)已知复数 z = ,则 z =
1+ i
(A) 1+ i (B) 1 i (C) 2 (D) 2
4
(3)在 ( x 2) 的展开式中 x3 项的系数为
(A) 8 (B)8 (C) 12 (D)12
(4)已知直线 x y + m = 0 与圆O : x2 + y2 = 2 相交于 A, B 两点,且 OAB 为等腰直角三角
形,则实数m 的值为
(A) 2 (B) 1 (C) 2 (D) 2
2
(5)下列函数中,以 π为周期,且在区间( , )上单调递增的是
2
(A) y = sin x (B) y = cos x (C) y = sin ( 2x + )(D) y = cos x
6
5
(6)若非零向量a,b满足 a = 2 b = 8,且向量a b与向量 a 的夹角是 ,则 (a b) b
6
的值为
(A) 24 (B) 24 (C)8 3 (D) 0
(7)已知等比数列 a 的公比为 q ,记n Tn = a1a2 an (n =1,2,3, ) ,则“ a 0 ,且 1
0 q 1 ”是“ T 为递减数列”的 n
(A)充分不必要条 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(8)某同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面 ABCD
是边长为 2 的正方形,△AEB ,△FBC ,△GCD ,△HDA均为正三角形,且它们所
在的平面都与平面 ABCD 垂直,则该包装盒的容积为( )
第1页/共15页
4 20
(A) (B) (C)10 32 3 + 6 (D)20
3 3 3
(9)已知 (x , y ) ,(x , y )是函数 y = ln x图象上两个不同的点,则下列 4 个式子中正确的是 1 1 2 2
y1+ yx + x 2
y
x + x 1
+ y2
① 1 2 e 2 ; ② 1 2 e 2 ;
2 2
2 y1 + y 2 y + y③ ln 2 ; ④ ln 1 2 .
x1 + x2 2 x1 + x2 2
(A)① ③ (B)② ③ (C)① ④ (D)② ④
sin x
(10)已知函数 f (x) = ,下列四个命题正确的序号是
x
3
① y = f (x) 是偶函数 ; ② f (x) 1;③当 x = 时, y = f (x) 取得极小值;④满足
2
n n +1
f ( ) f ( ) 的正整数 n的最小值为 9.
6 6
(A)① ② ③ (B)① ③ ④ (C)① ② (D)① ② ④
第二部分(非选择题 共 110 分)
二、填空题共 5 小题,每小题 5 分,共 25 分。
(11)抛物线 x2 = 10y 的焦点坐标是 .
(12)在平面直角坐标系 xOy 中,角 与角 均以Ox 为始边,它们的终边关于直线 y = x 对称.若
π 2π
, ,则 cos 的最小值为 .
6 3
2
(13)若直线 y = 2x与双曲线
y
x2 =1的右支只有一个公共点,则双曲线离心率的一个取值
m
为 .
(14)剪纸,又叫刻纸,是一种镂空艺术,是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下:取
一张半径为1的圆形纸片,记为 O ,在 O 内作内接正方形,接着在该正方形内作内切圆,记为
O ,并裁剪去该正方形内多余的部分(如图所示阴影部分),记为一次裁剪操1
作,……重复上述裁剪操作 n次,最终得到该剪纸.则第 4 次裁剪操作结束后所
得 O 的面积为 ;第 n次操作后,所有裁剪操作中裁剪去除的面积之和4
为 .
第2页/共15页
(15)不相同的数列 an 与 b ,且都不为常数数列,n M = k a ,给出下列 个结论: k = bk 4
①若数列 a , b 均为无穷等差数列且公差相等,则 M 中可能恰有一个元素; n n
②若数列 an 为递增数列,数列 bn 为递减数列,则 M 中恰有一个元素;
③若数列 a 为等差数列, b 为等比数列,则 M 中至多有三个元素; n n
④若数列 a , b 为公比不相等的等比数列,则 M 中至多有两个元素。 n n
其中所有错误结论的序号是 .
三、解答题共 6 小题,共 85 分。解答应写出文字说明,演算步骤或证明过程。
(16)(本小题 13 分)
在△ABC 中,已知b cosC a,c = 2 .
(Ⅰ)求证: B 是钝角;
(Ⅱ)请从下面三个条件中选择两个作为已知,使△ABC 存在且唯一确定,并求△ABC 的面积.
2 3
① b = 2 2 ; ② sinC = ; ③ sin B = .
2 2
注:如果选择的条件不符合要求,第(Ⅱ)问得 0 分;如果选择多个符合要求的条件分别解答,按第一个解
答计分.
(17)(本小题 13 分)
如图,在四棱锥 P ABCD 中,底面 ABCD 是平行四边形, PA⊥平面 ABCD ,平面 PAB ⊥平面 PAD ,
点 F 为线段 PD的中点, PA= AB = 2,直线 PC 与平面 ABCD 所成的角为30 .
(Ⅰ)若点G 为线段 BC 的中点,求证:CF // 平面 PAG ;
(Ⅱ)求二面角 B AF C 的余弦值;
(Ⅲ)求点 D 到平面 ABF 的距离.
(18)(本小题 14 分)
2019 年国产动画电影《哪吒之魔童降世》自上映以来斩获 50.35 亿票房,六年后,《哪吒之魔童闹海》
震撼上映,再次掀起观影热潮,票房最终或达150 亿,刷新多项纪录,成为中国电影的骄傲。下图是两部
电影第一天至第十三天上映期间的综合票房(亿元)及综合票房占比。其中条形图表示综合票房占比,折
线图为综合票房(亿元)。
图 1 《哪吒之魔童降世》综合票房及占比
第3页/共15页
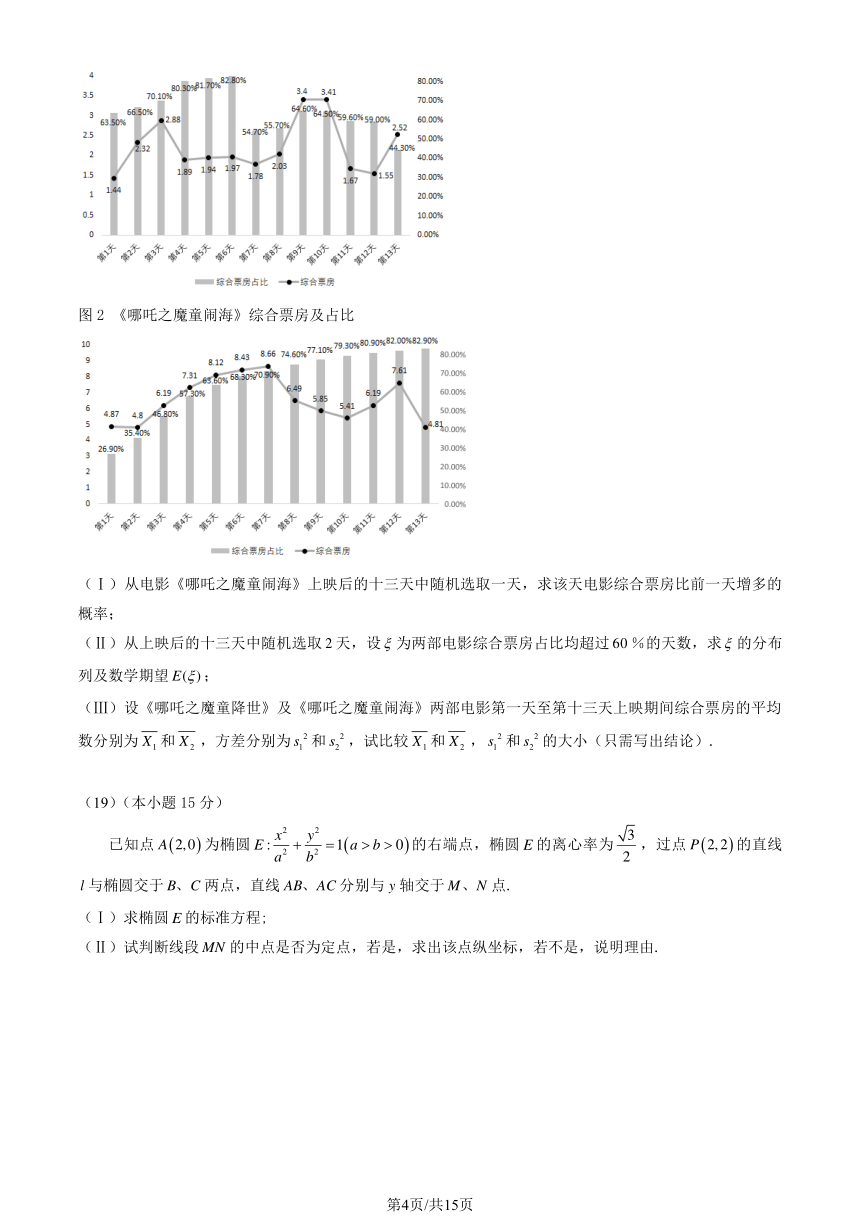
图 2 《哪吒之魔童闹海》综合票房及占比
(Ⅰ)从电影《哪吒之魔童闹海》上映后的十三天中随机选取一天,求该天电影综合票房比前一天增多的
概率;
(Ⅱ)从上映后的十三天中随机选取 2 天,设 为两部电影综合票房占比均超过 60 %的天数,求 的分布
列及数学期望 E( );
(Ⅲ)设《哪吒之魔童降世》及《哪吒之魔童闹海》两部电影第一天至第十三天上映期间综合票房的平均
数分别为 X1 和 X 2 ,方差分别为 s
2
1 和 s
2
2 ,试比较 X1 和 X
2 2
2 , s1 和 s2 的大小(只需写出结论).
(19)(本小题 15 分)
x2 y2 3
已知点 A(2,0)为椭圆 E : + =1(a b 0)的右端点,椭圆 E 的离心率为 ,过点 P (2,2)的直线
a2 b2 2
l 与椭圆交于 B、C 两点,直线 AB、AC 分别与 y 轴交于M、N 点.
(Ⅰ)求椭圆 E 的标准方程;
(Ⅱ)试判断线段 MN 的中点是否为定点,若是,求出该点纵坐标,若不是,说明理由.
第4页/共15页
(20)(本小题 15 分)
1 x
已知函数 f (x) = mx 1,
ex
(Ⅰ)当m = 0时,求曲线 f (x)在 (0, f (0))处的切线方程;
(Ⅱ)当m = 2时,求函数 f (x)的单调区间;
(Ⅲ)若 f (x)在 (0,+ ) 上存在零点,求实数m 的取值范围。
(21)(本小题 15 分)
已知数集 A = a1,a2 ,...,an (1= a1 a2 ... an ,n 2)具有性质 P :对任意的 k (2 k n) ,
i, j(1 i j n) ,使得 ak = ai + a j 成立.
(Ⅰ)分别判断数集{1,2,3,6,10}与{1,2,4,5,9} 是否具有性质 P ,并说明理由;
(Ⅱ)求证 an 2a1 + a2 + ...+ an 1(n 2) ;
(Ⅲ)若 an = 36 ,求数集 A中所有元素的和的最小值.
第5页/共15页
参考答案
第一部分(选择题 共 40 分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)D.
2i 2i
(2)C . z = = = 2 .
1+ i 1+ i
1 3 3
(3)A. 展开式中 x3 项为C4 x ( 2) = 8x
m
(4)C. 由题意: d =1, 即 =1,m = 2
2
π
(5)B. ABD 由图象判断,区间( , )长为 ,为 C 的半个周期,所以区间端点取最值,不符。
2 2
(7)D.
(7)D. 举反例: 4,2,1, ; 举反例: 0.1,0.1,0.1,
(8)C.
1
如图,把几何体补全为长方体,则 A1E = A1H = A1B1 =1,
2
AA 21 = AE A1E
2 = 22 12 = 3 ,
所以该包装盒的容积为
1 1 10 3
V , ABCD A1B1C1D 4V1 A A1EH = 2 2 3 4 1 1 3 =3 2 3
y1+ y2 ln x1+ln x2
(9)B. ln x x x + xe 2 = e 2 = e 1 2 = x 1 2 1x2
2
y1+ y2 x
e 2 1
+ x2 y 1
+ y2 x ln 1
+ x2 y 1
+ y2 x + x ln 1 2
2
= ln
2 2 2 2 2 x1 + x2
(10)D.
sin x
对①, f (x) = 定义域为,当 x 0 时,
x
sin( x) sin x sin x
f ( x) = = = = f (x) ,故 f (x) 是偶函数,①正确
x x x
sin x
对②,因为 f (x) = x x 0 为偶函数,故只需考虑 x 0 时的情况即可.
x
画出 y = sin x 与 y = x 的函数图像如图.因为 sin' x = cos x 1= x ' 且当 x = 0 时成立,由图可得当 x 0 时,
x sin x 恒成立.
sin x sin x sin x
故当 x 0 时, f (x) = 1 .又 f (x) = 为偶函数,故 f (x) = 1恒成立.
x x x
第6页/共15页
xcos x sin x
对③, f '(x) = 令 f '(x) = 0则 x cos x sin x = 0 .
x2
3
当 x = 时 x cos x sin x = 0 不成立,故③错误.
2
xcos x sin x
对④, f '(x) = 令 g(x) = xcos x sin x ,当 x = 时,
x2 2
g( ) = cos sin = 1,当 x 时, g(x) = xcos x sin x = cos x(x tan x)
2 2 2 2 2
先画出 y = x 与 y = tan x 的图像如图
1
注意当 x (0, ) 时, tan' x = 1,此时 x tan x ,此时 g(x) = cos x(x tan x) 0
2 cos2 x
当 x ( , )时, cos x 0 , x tan x ,故 g(x) = cos x(x tan x) 0
2
xcos x sin x
当 x = 时, g( ) = cos sin 0 .故当 x (0, ] 时, f '(x) = 0
x2
3
当 x ( , ) 时, cos x 0 ,且 x tan x = 0 有根.
2
sin x 6 7 3 9 2
又对 8 3 3f (x) = , f ( ) = 0 , f ( ) = , f ( ) = , f ( ) = ,
x 6 6 7 6 8 6 3
10 3 3 n n +1
f ( ) = .故满足 f ( ) f ( ) 的正整数 n的最小值为 9.
6 10 6 6
故④正确.
第二部分(非选择题 共 110 分)
二、填空题共 5 小题,每小题 5 分,共 25 分。
5
( 11) 0, .
2
第7页/共15页
5π 4π
(12)-1. 由题意,画出图形,得 + 2k , + 2k ,k Z ,所以 cos 的最小值为-1。
6 3
b
(13) e 5 .直线 y = 2x为双曲线的渐近线时, = 2,e = 5 ,由离心率的定义, e越大,开口越大,直
a
线与双曲线右支只有一个交点, e 5 。
1
(14) ; (4 π) 2 1 . 设 O 的半径为 R ,则 R = ,则第 n次裁剪操作得到的正方形边长为n i i
16 2
1
2
2R , O 的半径为
2 ,即 2
i i+1 R R = R
,
i i+1 i
2 2
i 1 i i
2 2 1 2故 Ri = R1 = =
,
2
2 2
i
1 π π π
O 的面积为i S = π = ,故 O 的面积为 = .
2 2i
4
24 16
n n
1
又第 n次裁剪操作的正方形边长为 1 2 1 22R = ,在该正方形的圆半径为 R = , n n
2 2
n n
1 2 2 n 2 n
故第 n次裁剪操作裁剪掉的面积为 1 2 1 2 1 1 π = π
2 2 2 2
1 π 4 π 1 1 1 1
= = ,所以第 n次裁剪操作裁剪掉的面积之和为 (4 π) + + ...+ = (4 π) 1 . n 2 n n 2 22 2n n 2 2 2 2
(15)①②④.
① 函数观点看数列,代表等差数列的两直线平行,所以无公共项;
② 举反例: a b 或者函数观点看数列,代表数列的两曲线交点横坐标不是正整数; 1 1
③ 函数观点看数列,当 q 0 且 q 1时,代表数列的两曲线可以有三个交点,所以 M 中至多有三个元
素;
④ 举反例:看数列取值规律,当两等比数列首项相等,公比相反时,有无数公共项。
三、解答题共 6 小题,共 85 分。解答应写出文字说明,演算步骤或证明过程。
(16)(本小题 13 分)
解:(I) b cosC a ,
a b
由正弦定理 = ,
sin A sin B
可得 sin B cosC sin A .…………………………………………………………1 分
又,在 ABC 中, A = π (B +C ),
所以 sin A = sin π (B +C ) = sin (B +C ) = sin BcosC + sinC cos B ,…………2 分
所以 sin B cosC sin B cosC + sin C cos B ,………………………………………3 分
即 sin C cos B 0 ,又 B,C (0,π) ,………………………………………………4 分
第8页/共15页
所以 sin C 0 , cos B 0 ,
所以 B 为钝角.………………………………………………………………5分
(II)选择①②不符合题意;
选择①③,即 3c = 2,b = 2 2,sin B = .………………………………………………6 分
2
B 1由 为钝角,得 cos B = .……………………………………………………7 分
2
2 2 2
b c =
由正弦定理 = ,得
6
3 sin C ,解得 sinC = .………………9分
sin B sinC 4
2
又 C 为锐角,得 10cosC = .……………………………………………………10 分
4
所以 30 6sin A = sin (B +C ) = sin BcosC + sinC cos B = .………………12 分
8
所以 的面积 1 15 3 ABC S = bcsin A = .………………………………13 分
2 2
选择②③,即 2 3c = 2,sinC = ,sin B = .………………………………6 分
2 2
b 2
b c =
由正弦定理 = 得 3 2 ,解得b = 6 .……………………8 分
sin B sinC
2 2
由 2 3
2π π
sinC = ,sin B = ,及 B 为钝角,C 为锐角,得 B = ,C = ,……9 分
2 2 3 4
π
所以 A = π (B +C ) = ,……………………………………………………10 分
12
π π π 6 2
所以 sin A = sin = sin = .……………………………………12 分
12 3 4 4
所以△ABC 的面积 .……………………………………13 分 1 3 3
S = bcsin A =
2 2
(17)(本小题 13 分)
解:法一:(Ⅰ)取 AP 的中点 M ,连接MF ,MG ;
因为 F , M 分别为 PD, PA的中点,
1
所以 MF / / AD ,MF = AD .
2
因为四边形 ABCD 是平行四边形,G 为线段 BC 的中点,
1
所以CG / / AD ,CG = AD,
2
所以CG / /MF ,CG = MF .
所以四边形 CGMF 为平行四边形,…… 2 分
第9页/共15页
所以CF / /GM .
因为GM 面PAG,CF 面PAG,
所以 CF∥平面 PAG .…… 4分
M
G
法二:(Ⅰ)取 AD的中点 E ,连接 EF , EC , AG , PG ;
因为 E, F 分别为 PD, AD 的中点,所以 EF / /PA, PA 平面 PAG ,
EF 平面 PAG ,所以 EF / / 平面 PAG ,
又因为G, E 分别为 BC, AD 的中点,四边形 ABCD 为平行四边形,
所以 AE / /GC 且 AE = GC ,则四边形 AGCE 为平行四边形,
所以CE / /GA,GA 平面 PAG ,CE 平面 PAG ,所以CE / / 平面 PAG ,
因为CE EF = E ,CE, EF 平面 EFC ,所以平面 PAG / / 平面 EFC ,
因为 FC 平面 EFC ,所以 FC / / 平面 PAG .
(II)因为 PA⊥平面 ABCD ,所以 PCA即为直线 PC 与平面 ABCD 所成的角,
由题意可知: PCA = 30 ,又 PA= AB = 2,所以 AC = 2 3 ,
因为 PA⊥平面 ABCD ,
所以 AB ⊥ PA, AD ⊥ PA
因为平面 PAD⊥平面 PAB ,平面 PAD 平面 PAB = PA,
所以 AB ⊥平面 PAD ,
所以 AB ⊥ AD ,
所以 AD = 2 2 且 AB , AP , AD两两垂直,
分别以 AB , AP , AD所在直线为 x轴, z 轴, y 轴如图建立空间直角坐标系,……6 分
第10页/共15页
则 A(0,0,0) , B(2,0,0) , F (0, 2,1) ,C(2,2 2,0) ,则 AB = (2,0,0), AF = (0, 2,1), AC = (2,2 2,0) ,
设平面 ABF 的法向量为m = (x , y , z ) ,平面 AFC 的法向量为1 1 1 n = (x , 2 , y2 , z2 )
m·AF = 0 2y + z
则有 1 1
= 0
,也即 ,令 z ,则1 = 2 m = (0, 2,2);…… 7 分
m·AB = 0 2x1 = 0
n·AF = 0 2y + z = 0
则有 ,也即
2 2
,令 z1 = 2 ,则 n = (2, 2,2) ,…… 8 分
n·AC = 0 2x2 + 2 2y2 = 0
m n 6 15
则 cos m,n = = = ,…… 10分
m n 2 + 4 4 + 2 + 4 5
由图可知:二面角 B AF C 为锐二面角,
所以二面角 15B AF C 的余弦值为 .…… 11 分
5
法一:(Ⅲ)因为 AD = (0,2 2,0)
AD m 4 2 6
所以点 D 到平面 ABF 的距离 d = = = …… 13 分
m 6 3
法二:(Ⅲ)因为 PA⊥平面 ABCD ,所以 PCA即为直线 PC 与平面 ABCD 所成的角,
由题意可知: PCA = 30 ,又 PA= AB = 2,所以 AC = 2 3 .
因为平面 PAD⊥平面 PAB ,且平面 PAD 平面 PAB = PA,因为 PA⊥平面 ABCD ,
所以 AB ⊥ PA,所以 AB ⊥平面 PAD , AD 平面 PAD ,所以 AB ⊥ AD ,
则四边形 ABCD 为矩形,因为 AB = 2, AC = 2 3 ,所以 AD = AC2 CD2 = 2 2 ,
设点 D 到平面 ABF 的距离为 h ,由 AB ⊥平面 PAD 可知: AB ⊥ AF ,
在Rt△PAD 中, PD = PA2 + AD2 = 2 3,
1
因为 F 为 PD的中点,所以 AF = PD = 3 ,
2
1 1 1 1
所以 S , , ABF = AB AF = 2 3 = 3 S ABD = AB AD = 2 2 2 = 2 2
2 2 2 2
因为 DC / / AB , AB 平面 ABF , DC 平面 ABF ,所以 DC / / 平面 ABF ,
所以点 D 到平面 ABF 的距离也就是直线CD 到平面 ABF 的距离.
第11页/共15页
1 1 1
因为VD ABF =V ,即F ABD S ABF h = S ABD AP ,
3 3 2
1 1
也即 ,所以 2 6 3 h = 2 2 1 h =
3 3 3
故直线CD 到平面
2 6
ABF 的距离为 .
3
(18)(本小题 14 分)
7
(Ⅰ)
12
C0 2 1 1 2 0
(Ⅱ) P( = 0) = 4
C9 6 C C= P( =1) = 4 9
6 C4 C9 1= P( = 2) = =
C213 13 C
2 2
13 13 C13 13
8
E( ) =
13
(Ⅲ) X < X , s 2 < s 21 2 1 2
(19)(本小题 15 分)
x2
解:(I)椭圆方程为 + y2 =1
4
(II)设 B (x1, y1 ),C ( x2 , y2 ),
因为直线 l 与椭圆交于 BC 两点,所以直线 BC 的斜率一定存在,故设直线 BC 的方程为: y = kx + m ,其中
m = 2(1 k ),
y = kx + m
由 x2 得:1+ 4k
2 x2 + 8kmx + 4m2 4 = 0 ,
+ y2 =1
4
2 2 2 2 3 8km 4m
2 4
Δ = 64k m 161+ 4k (m 1) 0,得 k ; x1 + x2 = , x1x2 =
8 1+ 4k 2 1+ 4k 2
y 2y 2y
又因为直线 AB 的方程: y = 1 (x 2),得M 0, 1 ,同理 N 0, 2
x1 2 x1 2 x2 2
2y1 2y由 + 2 =
x1 2 x2 2
(kx1 +m)(x2 2) + (kx2 +m)(x1 2) 2kx1x2 + (m 2k )(x1 + x2 ) 4m
2 = 2
(x1 2)(x2 2) x1x2 2(x1 + x2 ) + 4
第12页/共15页
2k (4m2 4) 8km(m 2k ) 4m(1+ 4k 2 )
= 2
(4m2 4) +16km + 4(1+ 4k 2 )
2k (4m2 4) 8km(m 2k ) 4m(1+ 4k 2 )
= 2
(4m2 4) +16km + 4(1+ 4k 2 )
8k 4m 4k + 2m 4k + 4(1 k )
= 2 = = =1
4m2 +16km +16k 2 m2 + 4km k 2 2+ 4 4(1 k ) +8k (1 k ) + 4k 2
1
故 MN 的中点为 0,
2
(20)(本小题 15 分)
1 x
解:(I))当m = 0时, f (x) = 1, f (0) = 0,切点为 (0,0) ,
ex
x 2
f (x) = , k = f (0) = 2,所以切线方程为: y = 2x
ex
1 x x 2
(II)当m = 2时, f (x) = + 2x 1, f (x) = + 2,
ex ex
x 2 3 x
令 g (x) = f (x) = + 2, g (x) = ,令g (x) = 0 x = 3
ex ex
x ( ,3)时,g (x) 0, g(x)在( ,3)单调递增,即f (x)在( ,3)单调递增
x (3,+ )时,g (x) 0, g(x)在(3,+ )单调递减,即f (x)在(3,+ )单调递减
因为 f (0) = 0,且x 3时,f (x) 0恒成立,
所以 x变化时,f (x)、f (x)的变化情况如下表
x ( ,0) 0 (0,+ )
f (x) 0 +
f (x) 极小值
所以 f (x)的单调递减区间为( ,0),单调递增区间为(0,+ )
1 x
(III) f (x) = mx 1,
ex
1 x
x (0,+ )时,1 x 1,ex 1, 1 0,若m 0,则f (x) 0恒成立,
ex
因为 f (x)在 (0,+ ) 上存在零点,所以m 0 ;
x 2
f (x) = m,由(II) f (x)在( ,3)单调递增,在(3,+ )单调递减
ex
1
f (x) max = f (3) = m, m 0, f (3) 0
e3
(1)若 f (0) 0,即 2 m 0 m 2时,
第13页/共15页
x 2
此时,x (0,3), f (x) f (0) 0, x (3,+ ), f (x) = m 0,
ex
x (0,+ ), f (x) 0, f (x)在(0,+ )单调递增, f (x) f (0) = 0
f (x)无零点
(2)若 f (0) 0,即 2 m 0 2 m 0时,
若 f (3) 0, x0 (0,3)使f (x ) = 0,x 3时f (x) 0 0
所以 x变化时,f (x)、f (x)的变化情况如下表
x ( , x ) x (x ,+ ) 0 0 0
f (x) 0 +
f (x) 极小值
f (x)在(0, x0 )上单调递减, f (x0 ) f (0) = 0, f (x)在(0, x0 )上无零点,
2
1+
2 2 t
f ( ) = m +1, 令 = t (1,+ ),h(t) = e t +1
m 2 m
e m
h (t) = et 1 0,h(t)单调递增, 所以h(t) h(1) e 0, et t +1 0,
2
1+
1 t 2
et t +1 0 1, m 1, f ( ) 0
et 2 m
e m
2
f (x0 ) f ( ) 0, f (x)在(x 0 ,+ )上存在零点,
m
综上,若 f (x)在 (0,+ ) 上存在零点,求实数m 的取值范围为 ( 2,0)
(21)(本小题 15 分)
解:(Ⅰ)∵10 无法表示,∴数集 1,2,3,6,10 不具有性质 P . ……2 分
∵ 2 =1+1, 4 = 2+ 2, 5 =1+ 4 , 9 = 4 + 5,∴数集{1,2,4,5,9} 具有性质 P .……4 分
(II)∵集合 A = a1,a2 , ,a 具有性质 即对任意的n P : k (2 k n), i , j (1 i j n)使得 ak = a j + a 成i
立,
又1= a , , 1 a2 an n≥ 2
∴ a a , a a ,……5 分 i k j k
a a , a a ,……6 分 i k 1 j k 1
∴ ak = a + a 2a ,……7 分 i j k 1
即 an 1 2a ,n 2 an 2 2a ,n 3 a3 2a ,2 a2 2a , 1
累加得 a2 + + an 1 + an 2(a1 + a2 + + a ),……8 分 n 1
化简得 a .……9 分 n 2a1 + a2 + + an 1
第14页/共15页
(Ⅲ)最小值为 75 .
首先注意到 a =1,根据性质 ,得到1 P a2 = 2a = 2 ,……10 分 1
所以易知数集 A的元素都是整数,
构造 A = 1,2,3,6,9,18,36 或者 A = 1,2,4,5,9,18,36 ,这两个集合具有性质 P ,此时元素和为 75 .下面证明
75 是最小的和.
n
假设数集 A = a1,a2 , ,an (a1 a2 an ,n 2) ,满足 S = ai 75最小,
i=1
第一步:首先说明集合 A = a ,a , ,a (a a a ,n 2) 中至少有 7 个元素: 1 2 n 1 2 n
由( 2 )可知, a2 2a ,1 a3 2a , ,又2 a1 =1,
∴ a , , , ,2 2 a3 4 an 8 a5 16 a6 32 36 , ∴ n 7 .……11 分
第二步:证明 an 1 =18, a = 9, n 2
若18 A,设 a , t =18
n
∵ a = 36 =18 +18,为了使 S = a 最小, n i
i=1
在集合 A中一定不含有元素 a ,使得18 a 36 ,从而 a =18; k k n 1
若18 A,根据性质 P ,对 an = 36,有 a , a ,使得 ,显然 ,∴ , i j an = 36 = ai + a j ai a j an + ai + a j = 72
此时集合 A中至少有 4 个不同于 a , a , a 的元素,从而n i j S (an + ai + a j ) + 4a = 76 ,矛盾, 1
∴18 A,且 an 1 =18.
同理可证: a = 9. n 2
至此,我们得到 a ,n 1 =18 a = 9, ……13 分 n 2
根据性质 P ,有 a , a ,使得 9 = a + a ,我们需要考虑如下几种情形: i j i j
① a =1, a = 8 ,此时集合中至少还需要一个大于等于 4 的元素 a ,才能得到元素 ,则 ; i j k 8 S 78
② a = 2 , a ,此时集合中至少还需要一个大于 的元素 ,才能得到元素 ,则 ; i j = 7 4 ak 7 S 78
③ a = 3, a = 6,此时集合j A = 1,2,3,6,9,18,36 , S = 75; i
④ a = 4 , a j = 5 ,此时集合 A = 1,2,4,5,9,18,36i , S = 75.
综上所述,若 an = 36,则数集 A中所有元素的和的最小值是 75 .……15 分
第15页/共15页
数 学
2025.2
第一部分(选择题 共 40 分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合 A = x x 3, x Z , B = x x2 1 ,则 A B =
(A) 1,0,1 (B) 3, 2,2,3 (C) 2,0,2 (D) 2,2
2i
(2)已知复数 z = ,则 z =
1+ i
(A) 1+ i (B) 1 i (C) 2 (D) 2
4
(3)在 ( x 2) 的展开式中 x3 项的系数为
(A) 8 (B)8 (C) 12 (D)12
(4)已知直线 x y + m = 0 与圆O : x2 + y2 = 2 相交于 A, B 两点,且 OAB 为等腰直角三角
形,则实数m 的值为
(A) 2 (B) 1 (C) 2 (D) 2
2
(5)下列函数中,以 π为周期,且在区间( , )上单调递增的是
2
(A) y = sin x (B) y = cos x (C) y = sin ( 2x + )(D) y = cos x
6
5
(6)若非零向量a,b满足 a = 2 b = 8,且向量a b与向量 a 的夹角是 ,则 (a b) b
6
的值为
(A) 24 (B) 24 (C)8 3 (D) 0
(7)已知等比数列 a 的公比为 q ,记n Tn = a1a2 an (n =1,2,3, ) ,则“ a 0 ,且 1
0 q 1 ”是“ T 为递减数列”的 n
(A)充分不必要条 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(8)某同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面 ABCD
是边长为 2 的正方形,△AEB ,△FBC ,△GCD ,△HDA均为正三角形,且它们所
在的平面都与平面 ABCD 垂直,则该包装盒的容积为( )
第1页/共15页
4 20
(A) (B) (C)10 32 3 + 6 (D)20
3 3 3
(9)已知 (x , y ) ,(x , y )是函数 y = ln x图象上两个不同的点,则下列 4 个式子中正确的是 1 1 2 2
y1+ yx + x 2
y
x + x 1
+ y2
① 1 2 e 2 ; ② 1 2 e 2 ;
2 2
2 y1 + y 2 y + y③ ln 2 ; ④ ln 1 2 .
x1 + x2 2 x1 + x2 2
(A)① ③ (B)② ③ (C)① ④ (D)② ④
sin x
(10)已知函数 f (x) = ,下列四个命题正确的序号是
x
3
① y = f (x) 是偶函数 ; ② f (x) 1;③当 x = 时, y = f (x) 取得极小值;④满足
2
n n +1
f ( ) f ( ) 的正整数 n的最小值为 9.
6 6
(A)① ② ③ (B)① ③ ④ (C)① ② (D)① ② ④
第二部分(非选择题 共 110 分)
二、填空题共 5 小题,每小题 5 分,共 25 分。
(11)抛物线 x2 = 10y 的焦点坐标是 .
(12)在平面直角坐标系 xOy 中,角 与角 均以Ox 为始边,它们的终边关于直线 y = x 对称.若
π 2π
, ,则 cos 的最小值为 .
6 3
2
(13)若直线 y = 2x与双曲线
y
x2 =1的右支只有一个公共点,则双曲线离心率的一个取值
m
为 .
(14)剪纸,又叫刻纸,是一种镂空艺术,是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下:取
一张半径为1的圆形纸片,记为 O ,在 O 内作内接正方形,接着在该正方形内作内切圆,记为
O ,并裁剪去该正方形内多余的部分(如图所示阴影部分),记为一次裁剪操1
作,……重复上述裁剪操作 n次,最终得到该剪纸.则第 4 次裁剪操作结束后所
得 O 的面积为 ;第 n次操作后,所有裁剪操作中裁剪去除的面积之和4
为 .
第2页/共15页
(15)不相同的数列 an 与 b ,且都不为常数数列,n M = k a ,给出下列 个结论: k = bk 4
①若数列 a , b 均为无穷等差数列且公差相等,则 M 中可能恰有一个元素; n n
②若数列 an 为递增数列,数列 bn 为递减数列,则 M 中恰有一个元素;
③若数列 a 为等差数列, b 为等比数列,则 M 中至多有三个元素; n n
④若数列 a , b 为公比不相等的等比数列,则 M 中至多有两个元素。 n n
其中所有错误结论的序号是 .
三、解答题共 6 小题,共 85 分。解答应写出文字说明,演算步骤或证明过程。
(16)(本小题 13 分)
在△ABC 中,已知b cosC a,c = 2 .
(Ⅰ)求证: B 是钝角;
(Ⅱ)请从下面三个条件中选择两个作为已知,使△ABC 存在且唯一确定,并求△ABC 的面积.
2 3
① b = 2 2 ; ② sinC = ; ③ sin B = .
2 2
注:如果选择的条件不符合要求,第(Ⅱ)问得 0 分;如果选择多个符合要求的条件分别解答,按第一个解
答计分.
(17)(本小题 13 分)
如图,在四棱锥 P ABCD 中,底面 ABCD 是平行四边形, PA⊥平面 ABCD ,平面 PAB ⊥平面 PAD ,
点 F 为线段 PD的中点, PA= AB = 2,直线 PC 与平面 ABCD 所成的角为30 .
(Ⅰ)若点G 为线段 BC 的中点,求证:CF // 平面 PAG ;
(Ⅱ)求二面角 B AF C 的余弦值;
(Ⅲ)求点 D 到平面 ABF 的距离.
(18)(本小题 14 分)
2019 年国产动画电影《哪吒之魔童降世》自上映以来斩获 50.35 亿票房,六年后,《哪吒之魔童闹海》
震撼上映,再次掀起观影热潮,票房最终或达150 亿,刷新多项纪录,成为中国电影的骄傲。下图是两部
电影第一天至第十三天上映期间的综合票房(亿元)及综合票房占比。其中条形图表示综合票房占比,折
线图为综合票房(亿元)。
图 1 《哪吒之魔童降世》综合票房及占比
第3页/共15页
图 2 《哪吒之魔童闹海》综合票房及占比
(Ⅰ)从电影《哪吒之魔童闹海》上映后的十三天中随机选取一天,求该天电影综合票房比前一天增多的
概率;
(Ⅱ)从上映后的十三天中随机选取 2 天,设 为两部电影综合票房占比均超过 60 %的天数,求 的分布
列及数学期望 E( );
(Ⅲ)设《哪吒之魔童降世》及《哪吒之魔童闹海》两部电影第一天至第十三天上映期间综合票房的平均
数分别为 X1 和 X 2 ,方差分别为 s
2
1 和 s
2
2 ,试比较 X1 和 X
2 2
2 , s1 和 s2 的大小(只需写出结论).
(19)(本小题 15 分)
x2 y2 3
已知点 A(2,0)为椭圆 E : + =1(a b 0)的右端点,椭圆 E 的离心率为 ,过点 P (2,2)的直线
a2 b2 2
l 与椭圆交于 B、C 两点,直线 AB、AC 分别与 y 轴交于M、N 点.
(Ⅰ)求椭圆 E 的标准方程;
(Ⅱ)试判断线段 MN 的中点是否为定点,若是,求出该点纵坐标,若不是,说明理由.
第4页/共15页
(20)(本小题 15 分)
1 x
已知函数 f (x) = mx 1,
ex
(Ⅰ)当m = 0时,求曲线 f (x)在 (0, f (0))处的切线方程;
(Ⅱ)当m = 2时,求函数 f (x)的单调区间;
(Ⅲ)若 f (x)在 (0,+ ) 上存在零点,求实数m 的取值范围。
(21)(本小题 15 分)
已知数集 A = a1,a2 ,...,an (1= a1 a2 ... an ,n 2)具有性质 P :对任意的 k (2 k n) ,
i, j(1 i j n) ,使得 ak = ai + a j 成立.
(Ⅰ)分别判断数集{1,2,3,6,10}与{1,2,4,5,9} 是否具有性质 P ,并说明理由;
(Ⅱ)求证 an 2a1 + a2 + ...+ an 1(n 2) ;
(Ⅲ)若 an = 36 ,求数集 A中所有元素的和的最小值.
第5页/共15页
参考答案
第一部分(选择题 共 40 分)
一、选择题共 10 小题,每小题 4 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)D.
2i 2i
(2)C . z = = = 2 .
1+ i 1+ i
1 3 3
(3)A. 展开式中 x3 项为C4 x ( 2) = 8x
m
(4)C. 由题意: d =1, 即 =1,m = 2
2
π
(5)B. ABD 由图象判断,区间( , )长为 ,为 C 的半个周期,所以区间端点取最值,不符。
2 2
(7)D.
(7)D. 举反例: 4,2,1, ; 举反例: 0.1,0.1,0.1,
(8)C.
1
如图,把几何体补全为长方体,则 A1E = A1H = A1B1 =1,
2
AA 21 = AE A1E
2 = 22 12 = 3 ,
所以该包装盒的容积为
1 1 10 3
V , ABCD A1B1C1D 4V1 A A1EH = 2 2 3 4 1 1 3 =3 2 3
y1+ y2 ln x1+ln x2
(9)B. ln x x x + xe 2 = e 2 = e 1 2 = x 1 2 1x2
2
y1+ y2 x
e 2 1
+ x2 y 1
+ y2 x ln 1
+ x2 y 1
+ y2 x + x ln 1 2
2
= ln
2 2 2 2 2 x1 + x2
(10)D.
sin x
对①, f (x) = 定义域为,当 x 0 时,
x
sin( x) sin x sin x
f ( x) = = = = f (x) ,故 f (x) 是偶函数,①正确
x x x
sin x
对②,因为 f (x) = x x 0 为偶函数,故只需考虑 x 0 时的情况即可.
x
画出 y = sin x 与 y = x 的函数图像如图.因为 sin' x = cos x 1= x ' 且当 x = 0 时成立,由图可得当 x 0 时,
x sin x 恒成立.
sin x sin x sin x
故当 x 0 时, f (x) = 1 .又 f (x) = 为偶函数,故 f (x) = 1恒成立.
x x x
第6页/共15页
xcos x sin x
对③, f '(x) = 令 f '(x) = 0则 x cos x sin x = 0 .
x2
3
当 x = 时 x cos x sin x = 0 不成立,故③错误.
2
xcos x sin x
对④, f '(x) = 令 g(x) = xcos x sin x ,当 x = 时,
x2 2
g( ) = cos sin = 1,当 x 时, g(x) = xcos x sin x = cos x(x tan x)
2 2 2 2 2
先画出 y = x 与 y = tan x 的图像如图
1
注意当 x (0, ) 时, tan' x = 1,此时 x tan x ,此时 g(x) = cos x(x tan x) 0
2 cos2 x
当 x ( , )时, cos x 0 , x tan x ,故 g(x) = cos x(x tan x) 0
2
xcos x sin x
当 x = 时, g( ) = cos sin 0 .故当 x (0, ] 时, f '(x) = 0
x2
3
当 x ( , ) 时, cos x 0 ,且 x tan x = 0 有根.
2
sin x 6 7 3 9 2
又对 8 3 3f (x) = , f ( ) = 0 , f ( ) = , f ( ) = , f ( ) = ,
x 6 6 7 6 8 6 3
10 3 3 n n +1
f ( ) = .故满足 f ( ) f ( ) 的正整数 n的最小值为 9.
6 10 6 6
故④正确.
第二部分(非选择题 共 110 分)
二、填空题共 5 小题,每小题 5 分,共 25 分。
5
( 11) 0, .
2
第7页/共15页
5π 4π
(12)-1. 由题意,画出图形,得 + 2k , + 2k ,k Z ,所以 cos 的最小值为-1。
6 3
b
(13) e 5 .直线 y = 2x为双曲线的渐近线时, = 2,e = 5 ,由离心率的定义, e越大,开口越大,直
a
线与双曲线右支只有一个交点, e 5 。
1
(14) ; (4 π) 2 1 . 设 O 的半径为 R ,则 R = ,则第 n次裁剪操作得到的正方形边长为n i i
16 2
1
2
2R , O 的半径为
2 ,即 2
i i+1 R R = R
,
i i+1 i
2 2
i 1 i i
2 2 1 2故 Ri = R1 = =
,
2
2 2
i
1 π π π
O 的面积为i S = π = ,故 O 的面积为 = .
2 2i
4
24 16
n n
1
又第 n次裁剪操作的正方形边长为 1 2 1 22R = ,在该正方形的圆半径为 R = , n n
2 2
n n
1 2 2 n 2 n
故第 n次裁剪操作裁剪掉的面积为 1 2 1 2 1 1 π = π
2 2 2 2
1 π 4 π 1 1 1 1
= = ,所以第 n次裁剪操作裁剪掉的面积之和为 (4 π) + + ...+ = (4 π) 1 . n 2 n n 2 22 2n n 2 2 2 2
(15)①②④.
① 函数观点看数列,代表等差数列的两直线平行,所以无公共项;
② 举反例: a b 或者函数观点看数列,代表数列的两曲线交点横坐标不是正整数; 1 1
③ 函数观点看数列,当 q 0 且 q 1时,代表数列的两曲线可以有三个交点,所以 M 中至多有三个元
素;
④ 举反例:看数列取值规律,当两等比数列首项相等,公比相反时,有无数公共项。
三、解答题共 6 小题,共 85 分。解答应写出文字说明,演算步骤或证明过程。
(16)(本小题 13 分)
解:(I) b cosC a ,
a b
由正弦定理 = ,
sin A sin B
可得 sin B cosC sin A .…………………………………………………………1 分
又,在 ABC 中, A = π (B +C ),
所以 sin A = sin π (B +C ) = sin (B +C ) = sin BcosC + sinC cos B ,…………2 分
所以 sin B cosC sin B cosC + sin C cos B ,………………………………………3 分
即 sin C cos B 0 ,又 B,C (0,π) ,………………………………………………4 分
第8页/共15页
所以 sin C 0 , cos B 0 ,
所以 B 为钝角.………………………………………………………………5分
(II)选择①②不符合题意;
选择①③,即 3c = 2,b = 2 2,sin B = .………………………………………………6 分
2
B 1由 为钝角,得 cos B = .……………………………………………………7 分
2
2 2 2
b c =
由正弦定理 = ,得
6
3 sin C ,解得 sinC = .………………9分
sin B sinC 4
2
又 C 为锐角,得 10cosC = .……………………………………………………10 分
4
所以 30 6sin A = sin (B +C ) = sin BcosC + sinC cos B = .………………12 分
8
所以 的面积 1 15 3 ABC S = bcsin A = .………………………………13 分
2 2
选择②③,即 2 3c = 2,sinC = ,sin B = .………………………………6 分
2 2
b 2
b c =
由正弦定理 = 得 3 2 ,解得b = 6 .……………………8 分
sin B sinC
2 2
由 2 3
2π π
sinC = ,sin B = ,及 B 为钝角,C 为锐角,得 B = ,C = ,……9 分
2 2 3 4
π
所以 A = π (B +C ) = ,……………………………………………………10 分
12
π π π 6 2
所以 sin A = sin = sin = .……………………………………12 分
12 3 4 4
所以△ABC 的面积 .……………………………………13 分 1 3 3
S = bcsin A =
2 2
(17)(本小题 13 分)
解:法一:(Ⅰ)取 AP 的中点 M ,连接MF ,MG ;
因为 F , M 分别为 PD, PA的中点,
1
所以 MF / / AD ,MF = AD .
2
因为四边形 ABCD 是平行四边形,G 为线段 BC 的中点,
1
所以CG / / AD ,CG = AD,
2
所以CG / /MF ,CG = MF .
所以四边形 CGMF 为平行四边形,…… 2 分
第9页/共15页
所以CF / /GM .
因为GM 面PAG,CF 面PAG,
所以 CF∥平面 PAG .…… 4分
M
G
法二:(Ⅰ)取 AD的中点 E ,连接 EF , EC , AG , PG ;
因为 E, F 分别为 PD, AD 的中点,所以 EF / /PA, PA 平面 PAG ,
EF 平面 PAG ,所以 EF / / 平面 PAG ,
又因为G, E 分别为 BC, AD 的中点,四边形 ABCD 为平行四边形,
所以 AE / /GC 且 AE = GC ,则四边形 AGCE 为平行四边形,
所以CE / /GA,GA 平面 PAG ,CE 平面 PAG ,所以CE / / 平面 PAG ,
因为CE EF = E ,CE, EF 平面 EFC ,所以平面 PAG / / 平面 EFC ,
因为 FC 平面 EFC ,所以 FC / / 平面 PAG .
(II)因为 PA⊥平面 ABCD ,所以 PCA即为直线 PC 与平面 ABCD 所成的角,
由题意可知: PCA = 30 ,又 PA= AB = 2,所以 AC = 2 3 ,
因为 PA⊥平面 ABCD ,
所以 AB ⊥ PA, AD ⊥ PA
因为平面 PAD⊥平面 PAB ,平面 PAD 平面 PAB = PA,
所以 AB ⊥平面 PAD ,
所以 AB ⊥ AD ,
所以 AD = 2 2 且 AB , AP , AD两两垂直,
分别以 AB , AP , AD所在直线为 x轴, z 轴, y 轴如图建立空间直角坐标系,……6 分
第10页/共15页
则 A(0,0,0) , B(2,0,0) , F (0, 2,1) ,C(2,2 2,0) ,则 AB = (2,0,0), AF = (0, 2,1), AC = (2,2 2,0) ,
设平面 ABF 的法向量为m = (x , y , z ) ,平面 AFC 的法向量为1 1 1 n = (x , 2 , y2 , z2 )
m·AF = 0 2y + z
则有 1 1
= 0
,也即 ,令 z ,则1 = 2 m = (0, 2,2);…… 7 分
m·AB = 0 2x1 = 0
n·AF = 0 2y + z = 0
则有 ,也即
2 2
,令 z1 = 2 ,则 n = (2, 2,2) ,…… 8 分
n·AC = 0 2x2 + 2 2y2 = 0
m n 6 15
则 cos m,n = = = ,…… 10分
m n 2 + 4 4 + 2 + 4 5
由图可知:二面角 B AF C 为锐二面角,
所以二面角 15B AF C 的余弦值为 .…… 11 分
5
法一:(Ⅲ)因为 AD = (0,2 2,0)
AD m 4 2 6
所以点 D 到平面 ABF 的距离 d = = = …… 13 分
m 6 3
法二:(Ⅲ)因为 PA⊥平面 ABCD ,所以 PCA即为直线 PC 与平面 ABCD 所成的角,
由题意可知: PCA = 30 ,又 PA= AB = 2,所以 AC = 2 3 .
因为平面 PAD⊥平面 PAB ,且平面 PAD 平面 PAB = PA,因为 PA⊥平面 ABCD ,
所以 AB ⊥ PA,所以 AB ⊥平面 PAD , AD 平面 PAD ,所以 AB ⊥ AD ,
则四边形 ABCD 为矩形,因为 AB = 2, AC = 2 3 ,所以 AD = AC2 CD2 = 2 2 ,
设点 D 到平面 ABF 的距离为 h ,由 AB ⊥平面 PAD 可知: AB ⊥ AF ,
在Rt△PAD 中, PD = PA2 + AD2 = 2 3,
1
因为 F 为 PD的中点,所以 AF = PD = 3 ,
2
1 1 1 1
所以 S , , ABF = AB AF = 2 3 = 3 S ABD = AB AD = 2 2 2 = 2 2
2 2 2 2
因为 DC / / AB , AB 平面 ABF , DC 平面 ABF ,所以 DC / / 平面 ABF ,
所以点 D 到平面 ABF 的距离也就是直线CD 到平面 ABF 的距离.
第11页/共15页
1 1 1
因为VD ABF =V ,即F ABD S ABF h = S ABD AP ,
3 3 2
1 1
也即 ,所以 2 6 3 h = 2 2 1 h =
3 3 3
故直线CD 到平面
2 6
ABF 的距离为 .
3
(18)(本小题 14 分)
7
(Ⅰ)
12
C0 2 1 1 2 0
(Ⅱ) P( = 0) = 4
C9 6 C C= P( =1) = 4 9
6 C4 C9 1= P( = 2) = =
C213 13 C
2 2
13 13 C13 13
8
E( ) =
13
(Ⅲ) X < X , s 2 < s 21 2 1 2
(19)(本小题 15 分)
x2
解:(I)椭圆方程为 + y2 =1
4
(II)设 B (x1, y1 ),C ( x2 , y2 ),
因为直线 l 与椭圆交于 BC 两点,所以直线 BC 的斜率一定存在,故设直线 BC 的方程为: y = kx + m ,其中
m = 2(1 k ),
y = kx + m
由 x2 得:1+ 4k
2 x2 + 8kmx + 4m2 4 = 0 ,
+ y2 =1
4
2 2 2 2 3 8km 4m
2 4
Δ = 64k m 161+ 4k (m 1) 0,得 k ; x1 + x2 = , x1x2 =
8 1+ 4k 2 1+ 4k 2
y 2y 2y
又因为直线 AB 的方程: y = 1 (x 2),得M 0, 1 ,同理 N 0, 2
x1 2 x1 2 x2 2
2y1 2y由 + 2 =
x1 2 x2 2
(kx1 +m)(x2 2) + (kx2 +m)(x1 2) 2kx1x2 + (m 2k )(x1 + x2 ) 4m
2 = 2
(x1 2)(x2 2) x1x2 2(x1 + x2 ) + 4
第12页/共15页
2k (4m2 4) 8km(m 2k ) 4m(1+ 4k 2 )
= 2
(4m2 4) +16km + 4(1+ 4k 2 )
2k (4m2 4) 8km(m 2k ) 4m(1+ 4k 2 )
= 2
(4m2 4) +16km + 4(1+ 4k 2 )
8k 4m 4k + 2m 4k + 4(1 k )
= 2 = = =1
4m2 +16km +16k 2 m2 + 4km k 2 2+ 4 4(1 k ) +8k (1 k ) + 4k 2
1
故 MN 的中点为 0,
2
(20)(本小题 15 分)
1 x
解:(I))当m = 0时, f (x) = 1, f (0) = 0,切点为 (0,0) ,
ex
x 2
f (x) = , k = f (0) = 2,所以切线方程为: y = 2x
ex
1 x x 2
(II)当m = 2时, f (x) = + 2x 1, f (x) = + 2,
ex ex
x 2 3 x
令 g (x) = f (x) = + 2, g (x) = ,令g (x) = 0 x = 3
ex ex
x ( ,3)时,g (x) 0, g(x)在( ,3)单调递增,即f (x)在( ,3)单调递增
x (3,+ )时,g (x) 0, g(x)在(3,+ )单调递减,即f (x)在(3,+ )单调递减
因为 f (0) = 0,且x 3时,f (x) 0恒成立,
所以 x变化时,f (x)、f (x)的变化情况如下表
x ( ,0) 0 (0,+ )
f (x) 0 +
f (x) 极小值
所以 f (x)的单调递减区间为( ,0),单调递增区间为(0,+ )
1 x
(III) f (x) = mx 1,
ex
1 x
x (0,+ )时,1 x 1,ex 1, 1 0,若m 0,则f (x) 0恒成立,
ex
因为 f (x)在 (0,+ ) 上存在零点,所以m 0 ;
x 2
f (x) = m,由(II) f (x)在( ,3)单调递增,在(3,+ )单调递减
ex
1
f (x) max = f (3) = m, m 0, f (3) 0
e3
(1)若 f (0) 0,即 2 m 0 m 2时,
第13页/共15页
x 2
此时,x (0,3), f (x) f (0) 0, x (3,+ ), f (x) = m 0,
ex
x (0,+ ), f (x) 0, f (x)在(0,+ )单调递增, f (x) f (0) = 0
f (x)无零点
(2)若 f (0) 0,即 2 m 0 2 m 0时,
若 f (3) 0, x0 (0,3)使f (x ) = 0,x 3时f (x) 0 0
所以 x变化时,f (x)、f (x)的变化情况如下表
x ( , x ) x (x ,+ ) 0 0 0
f (x) 0 +
f (x) 极小值
f (x)在(0, x0 )上单调递减, f (x0 ) f (0) = 0, f (x)在(0, x0 )上无零点,
2
1+
2 2 t
f ( ) = m +1, 令 = t (1,+ ),h(t) = e t +1
m 2 m
e m
h (t) = et 1 0,h(t)单调递增, 所以h(t) h(1) e 0, et t +1 0,
2
1+
1 t 2
et t +1 0 1, m 1, f ( ) 0
et 2 m
e m
2
f (x0 ) f ( ) 0, f (x)在(x 0 ,+ )上存在零点,
m
综上,若 f (x)在 (0,+ ) 上存在零点,求实数m 的取值范围为 ( 2,0)
(21)(本小题 15 分)
解:(Ⅰ)∵10 无法表示,∴数集 1,2,3,6,10 不具有性质 P . ……2 分
∵ 2 =1+1, 4 = 2+ 2, 5 =1+ 4 , 9 = 4 + 5,∴数集{1,2,4,5,9} 具有性质 P .……4 分
(II)∵集合 A = a1,a2 , ,a 具有性质 即对任意的n P : k (2 k n), i , j (1 i j n)使得 ak = a j + a 成i
立,
又1= a , , 1 a2 an n≥ 2
∴ a a , a a ,……5 分 i k j k
a a , a a ,……6 分 i k 1 j k 1
∴ ak = a + a 2a ,……7 分 i j k 1
即 an 1 2a ,n 2 an 2 2a ,n 3 a3 2a ,2 a2 2a , 1
累加得 a2 + + an 1 + an 2(a1 + a2 + + a ),……8 分 n 1
化简得 a .……9 分 n 2a1 + a2 + + an 1
第14页/共15页
(Ⅲ)最小值为 75 .
首先注意到 a =1,根据性质 ,得到1 P a2 = 2a = 2 ,……10 分 1
所以易知数集 A的元素都是整数,
构造 A = 1,2,3,6,9,18,36 或者 A = 1,2,4,5,9,18,36 ,这两个集合具有性质 P ,此时元素和为 75 .下面证明
75 是最小的和.
n
假设数集 A = a1,a2 , ,an (a1 a2 an ,n 2) ,满足 S = ai 75最小,
i=1
第一步:首先说明集合 A = a ,a , ,a (a a a ,n 2) 中至少有 7 个元素: 1 2 n 1 2 n
由( 2 )可知, a2 2a ,1 a3 2a , ,又2 a1 =1,
∴ a , , , ,2 2 a3 4 an 8 a5 16 a6 32 36 , ∴ n 7 .……11 分
第二步:证明 an 1 =18, a = 9, n 2
若18 A,设 a , t =18
n
∵ a = 36 =18 +18,为了使 S = a 最小, n i
i=1
在集合 A中一定不含有元素 a ,使得18 a 36 ,从而 a =18; k k n 1
若18 A,根据性质 P ,对 an = 36,有 a , a ,使得 ,显然 ,∴ , i j an = 36 = ai + a j ai a j an + ai + a j = 72
此时集合 A中至少有 4 个不同于 a , a , a 的元素,从而n i j S (an + ai + a j ) + 4a = 76 ,矛盾, 1
∴18 A,且 an 1 =18.
同理可证: a = 9. n 2
至此,我们得到 a ,n 1 =18 a = 9, ……13 分 n 2
根据性质 P ,有 a , a ,使得 9 = a + a ,我们需要考虑如下几种情形: i j i j
① a =1, a = 8 ,此时集合中至少还需要一个大于等于 4 的元素 a ,才能得到元素 ,则 ; i j k 8 S 78
② a = 2 , a ,此时集合中至少还需要一个大于 的元素 ,才能得到元素 ,则 ; i j = 7 4 ak 7 S 78
③ a = 3, a = 6,此时集合j A = 1,2,3,6,9,18,36 , S = 75; i
④ a = 4 , a j = 5 ,此时集合 A = 1,2,4,5,9,18,36i , S = 75.
综上所述,若 an = 36,则数集 A中所有元素的和的最小值是 75 .……15 分
第15页/共15页
同课章节目录
