【2025春新教材】人教版七年级下册数学11.1.2 不等式的性质(教学设计)
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学11.1.2 不等式的性质(教学设计) |  | |
| 格式 | zip | ||
| 文件大小 | 939.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 12:58:10 | ||
图片预览



文档简介
/ 让教学更有效 高效备课 | 数学学科
11.1.2不等式的性质 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第十一章“不等式与不等式组”11.1.2 不等式的性质,内容包括:掌握不等式的基本事实和性质,会利用不等式的性质求出不等式的解集,并能在数轴上表示其解集.
2.内容解析
不等式的性质在初中数学知识体系中占据关键位置,与前后知识紧密相连.从知识的承接来看,学生此前已学习有理数的大小比较,这为理解不等式的基本事实奠定了基础.同时,等式性质的学习让学生熟悉了等式变形规则,在探究不等式性质时,可通过类比等式性质,助力学生快速掌握不等式性质.
从后续知识关联而言,不等式性质是解各类不等式(如一元一次不等式、一元一次不等式组)的核心依据,为解决含不等关系的实际问题提供理论支撑,也为高中进一步学习不等式的综合运用筑牢根基.
基于以上分析,确定本节课的教学重点为:掌握不等式的性质1,2,3.
二、目标和目标解析
1.目标
(1)掌握不等式的基本事实和性质,会利用不等式的性质求出不等式的解集,并能在数轴上表示其解集.
(2)经历不等式性质的探索过程,培养观察和推理能力、体会类比思想,分类讨论思想和数学归纳思想.
(3)用不等式的基本性质解简单的不等式,培养应用意识,发展运算能力.
2.目标解析
(1)学生需要理解不等式的基本事实中数的大小关系与不等式符号的联系.对于不等式的性质,不仅要知道文字表述,更要能通过具体例子进行验证、运用和理解.学生要能够根据给定的不等式,正确运用性质进行变形,逐步求出使不等式成立的未知数的取值范围.在数轴上表示解集,学生要掌握用实心点或空心点表示端点值,以及根据不等号方向确定取值范围在数轴上的表示方法.
(2)在探索不等式的性质时,学生通过观察不同的不等式在进行加、减、乘、除运算后,不等号的变化情况,归纳总结出一般性的性质,培养观察和数学归纳能力.学生在等式性质的基础上,发现不等式性质与等式性质有相似之处,但在乘除负数时又有不同,在体会类比思想的同时加深对不等式性质的理解.分类讨论思想在研究不等式两边乘(或除以)同一个数时体现明显.因为乘(或除以)正数和负数时不等号方向变化不同,所以需要分类讨论,让学生明白不同情况下的处理方式.
(3)学生要能将实际问题中的不等关系抽象为不等式模型,然后运用不等式性质求解,培养应用意识.在解不等式的过程中,学生要熟练运用不等式的性质进行去分母、去括号、移项、合并同类项、系数化为1等运算,逐步提高运算的准确性和速度,发展运算能力.
三、教学问题诊断分析
1.学生对不等式的性质理解困难:
不等式的性质较为抽象,尤其是涉及到乘除负数时不等号方向改变,学生容易与等式性质混淆,难以理解其本质原因.因此在教学过程中,需要通过大量具体数字的例子,让学生自主计算并观察不等号方向的变化,引导学生思考变化原因.同时,利用数轴直观展示数的大小变化与不等号方向的关系,帮助学生理解.
2.求解不等式解集时出错:
在运用不等式的性质求解不等式时,学生可能会在去分母、系数化为1的过程中出现运算错误,或者在处理不等号方向时出错.因此在教学过程中,需要加强对运算步骤的规范训练,每一步变形都要让学生说明依据.通过小组竞赛等形式,让学生相互检查纠错,提高运算的准确性.对于容易出错的乘除负数改变不等号方向的情况,进行专项练习和强调.
基于以上分析,确定本节课的教学难点为:探索并理解不等式的性质3.
四、教学过程设计
(一)复习引入
问题1 直接说出下列不等式的解集.
(1)x+4>10 (2)2x<6 (3)
解:(1)x>6 (2)x<3 (3)直接得出它的解集比较困难,因此要讨论怎样解不等式.
问题2 解一元一次方程的步骤有哪些?解方程的依据是什么?
答:解一元一次方程的步骤有:去分母,去括号,移项,合并同类项,系数化为一.
解方程的依据是:等式的性质.
问题3 你能说说等式有哪些性质吗?
答:等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
(二)合作探究
关于不等式的基本事实
(1)交换不等式两边,不等号的方向改变:如果a>b,那么b<a.
(2)不等关系可以传递:如果a>b,b>c,那么a>c.
借助数轴理解这两个基本事实
探究1 用 “>”或 “<”填空,并观察不等号的方向是否改变,总结其中的规律:
(1)5>3, (2)-1<3,
5+2 > 3+2, -1+4 < 3+4,
5+0 > 3+0, -1+0 < 3+0,
5+(-2) > 3+(-2); -1+(-7) < 3+(-7).
根据发现的规律填空:不等式两边加同一个数,不等号的方向不变.
不等式两边减同一个数,不等号的方向不变.
追问 换一些其他数,验证这个发现.
不等式的性质1
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c>b±c.
探究2 用 “>”或 “<”填空,并观察不等号的方向是否改变,总结其中的规律:
(1)6>2, (2)-2<3,
6×5 > 2×5, -2×4 < 3×4,
6×(-5) < 2×(-5); -2×(-0.5) > 3×(-0.5).
根据发现的规律填空:不等式两边乘同一个正数,不等号的方向不变.
不等式两边乘同一个负数,不等号的方向改变.
不等式两边除以同一个正数,不等号的方向不变.
不等式两边除以同一个负数,不等号的方向改变.
追问 如果不等式两边乘0,结果又如何呢?
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,那么ac>bc(或 > ).
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c<0,那么ac<bc(或 < ).
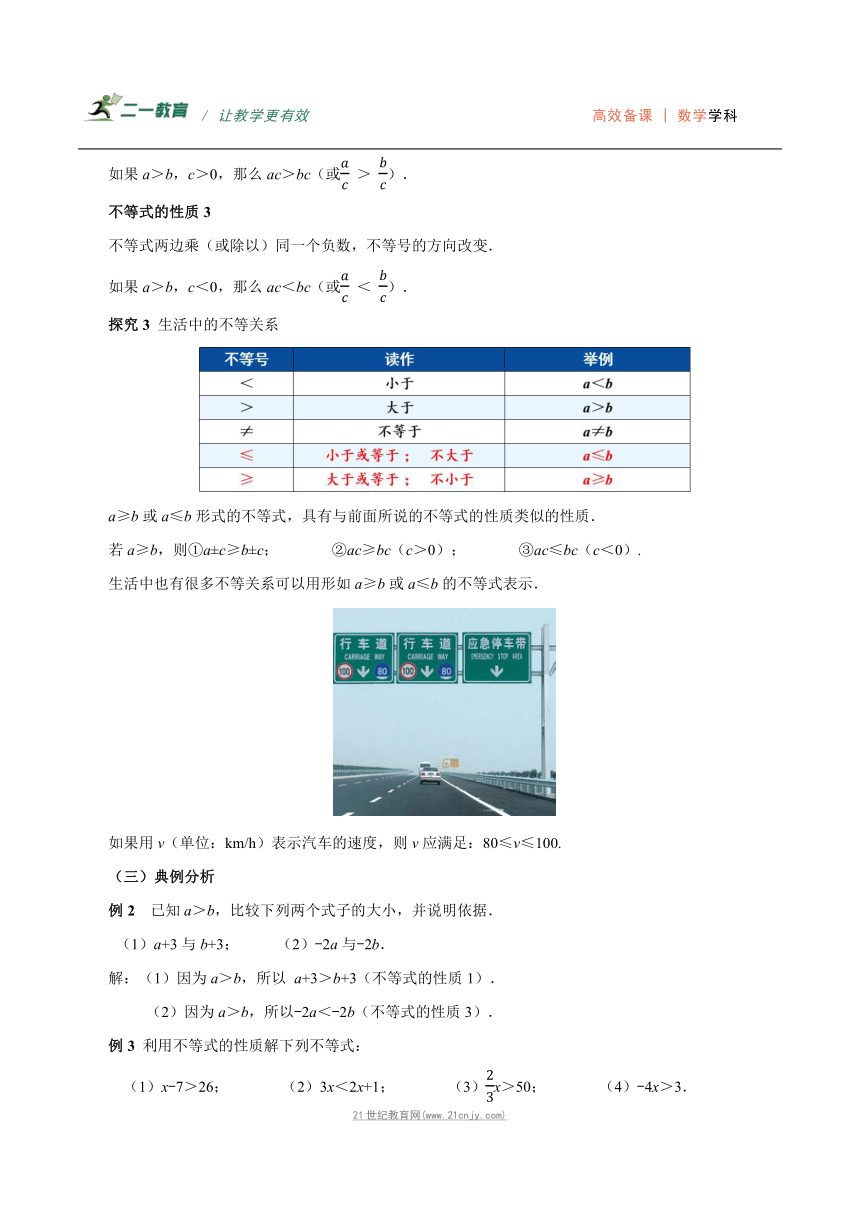
探究3 生活中的不等关系
a≥b或a≤b形式的不等式,具有与前面所说的不等式的性质类似的性质.
若a≥b,则①a±c≥b±c; ②ac≥bc(c>0); ③ac≤bc(c<0).
生活中也有很多不等关系可以用形如a≥b或a≤b的不等式表示.
如果用v(单位:km/h)表示汽车的速度,则v应满足:80≤v≤100.
(三)典例分析
例2 已知a>b,比较下列两个式子的大小,并说明依据.
(1)a+3与b+3; (2)-2a与-2b.
解:(1)因为a>b,所以 a+3>b+3(不等式的性质1).
因为a>b,所以-2a<-2b(不等式的性质3).
例3 利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1; (3)x>50; (4)-4x>3.
借助不等式的性质,将不等式逐步化为x>m或x<m (m为常数) 的形式.
解:(1)根据不等式的性质1,不等式两边加7,不等号的方向不变,所以
x-7+7>26+7,
x>33.
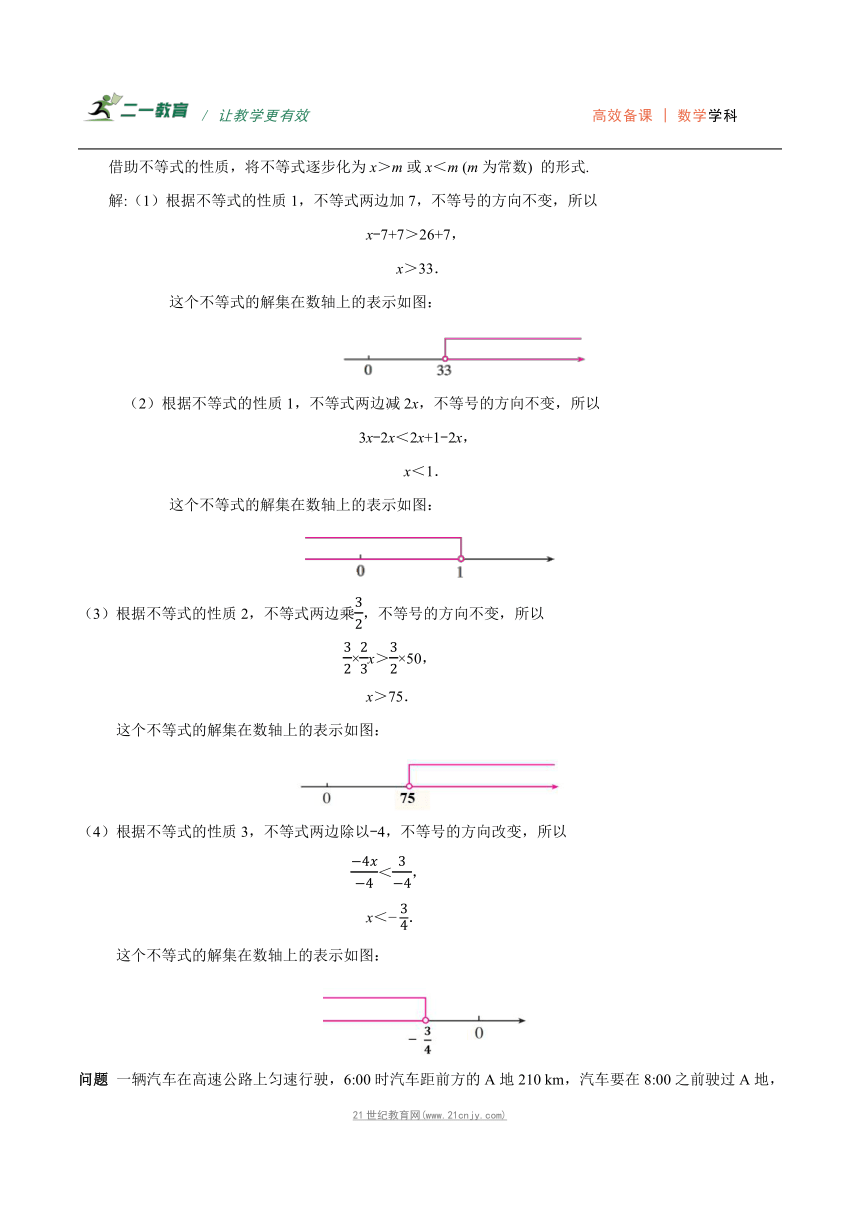
这个不等式的解集在数轴上的表示如图:
(2)根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以
3x-2x<2x+1-2x,
x<1.
这个不等式的解集在数轴上的表示如图:
(3)根据不等式的性质2,不等式两边乘,不等号的方向不变,所以
×x>×50,
x>75.
这个不等式的解集在数轴上的表示如图:
(4)根据不等式的性质3,不等式两边除以-4,不等号的方向改变,所以
<,
x<.
这个不等式的解集在数轴上的表示如图:
问题 一辆汽车在高速公路上匀速行驶,6:00时汽车距前方的A地210 km,汽车要在8:00之前驶过A地,且汽车所行驶道路的最高限速是120 km/h,车速应满足什么条件?
解:设车速是x km/h.从路程上看,就是以x km/h的速度行驶2 h的路程要超过210 km,这个不等关系可以表示为
2x>210
解得 x>105.
因为汽车所行驶道路的最高限速是120 km/h,所以车速应满足105例4 如图,一个长方体形状的鱼缸长10 dm,宽3.5 dm,高7 dm.若鱼缸内已有水的高度为1 dm,现准备向鱼缸内继续注水.用V(单位:dm3)表示新注入水的体积,写出V的取值范围并在数轴上表示.
分析 问题中的不等关系是:已有水的体积与新注入水的体积之和不能超过鱼缸的容积.
解:因为 “已有水的体积+新注入水的体积V≤鱼缸的容积”,所以
10×3.5×1+V≤10×3.5×7,
解得 V≤210.
又由于新注入水的体积V不能是负数,所以V的取值范围是0≤V≤210.
在数轴上表示V的取值范围如图所示.
(四)巩固练习
1. 已知p>q,用 “>”或 “<”填空,并说明依据:
(1)p+ > q+; 不等式的性质1 (2)p-2 > q-2; 不等式的性质1
(3)p+2m > q+2m; 不等式的性质1 (4)-5p < -5q; 不等式的性质3
(5) > ; 不等式的性质2 (6)4p+1 < 4q+1.不等式的性质2和性质1
2. 已知m>3,利用不等式的性质写出下列各式的取值范围:
(1)m+5; (2); (3)-2m; (4)3m-4.
解:(1)m+5>8;不等式的性质1 (2)>;不等式的性质2
(3)-2m<-6;不等式的性质3 (4)3m-4>5.不等式的性质2和性质1
3.已知a>b,用 “<”或 “>”填空,并说明依据:
(1)2a-5 > 2b-5;不等式的性质2,不等式的性质1.
(2)-3.5b+1 > -3.5a+1.不等式的基本事实,不等式的性质3,不等式的性质1.
4. 关于x的不等式的解集在数轴上的表示如图所示,写出相应的解集.
(1)(2)(3)
解:(1)x≥-2 (2)x<3 (3)-15. 利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+5>-1; (2)4x<3x+5; (3) x ≤ ; (4)-8x>10.
6. 某日北京的最低气温是19 ℃,最高气温是28 ℃,用不等式表示这天的气温t(单位:℃)的变化范围.
解:气温t(单位:℃)的变化范围是197. 如图是某机器零件的设计图纸 (图中长度单位:mm),用不等式表示零件长度L的合格尺寸 (L的取值范围).
解:零件长度L的合格尺寸是39.98≤L≤40.02.
8. 用不等式表示下列不等关系,写出解集并在数轴上表示解集:
(1)x的3倍大于1; (2)x与3的和不小于7;
(3)y的小于或等于-2; (4)y的2倍小于y与1的差.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
归纳总结
思考 比较不等式的性质2和性质3,指出它们有什么区别.再比较不等式的性质和等式的性质,它们有什么异同?
答:等式的性质有两条,它们表明了等式两边进行同样的加(减)、乘(除)运算时,相等关系不变.
不等式的性质有三条,它们表明了不等式两边进行同样的加(减)、乘(除)运算时,大小关系有时不变,有时改变. 对于乘法和除法运算,不等式的性质要分两种情况论述.
感受中考
1.(2024 长春)不等关系在生活中广泛存在.如图,a、b分别表示两位同学的身高,c表示台阶的高度.图中两人的对话体现的数学原理是(A)
A.若a>b,则a+c>b+c B.若a>b,b>c,则a>c
C.若a>b,c>0,则ac>bc D.若a>b,c>0,则
2.(2024 苏州)若a>b﹣1,则下列结论一定正确的是(D)
A.a+1<b B.a﹣1<b C.a>b D.a+1>b
3.(2024 内江)不等式3x≥x﹣4的解集是(A)
A.x≥﹣2 B.x≤﹣2 C.x>﹣2 D.x<﹣2
4.(2024 湖北)不等式x+1≥2的解集在数轴上表示正确的是(A)
A. B.
C. D.
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(七)小结梳理
(八)布置作业
1.必做题:习题11.1 第4题,第5题,第6题.
2.探究性作业:习题11.1 第11题,第12题.
五、教学反思
21世纪教育网(www.21cnjy.com)
11.1.2不等式的性质 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第十一章“不等式与不等式组”11.1.2 不等式的性质,内容包括:掌握不等式的基本事实和性质,会利用不等式的性质求出不等式的解集,并能在数轴上表示其解集.
2.内容解析
不等式的性质在初中数学知识体系中占据关键位置,与前后知识紧密相连.从知识的承接来看,学生此前已学习有理数的大小比较,这为理解不等式的基本事实奠定了基础.同时,等式性质的学习让学生熟悉了等式变形规则,在探究不等式性质时,可通过类比等式性质,助力学生快速掌握不等式性质.
从后续知识关联而言,不等式性质是解各类不等式(如一元一次不等式、一元一次不等式组)的核心依据,为解决含不等关系的实际问题提供理论支撑,也为高中进一步学习不等式的综合运用筑牢根基.
基于以上分析,确定本节课的教学重点为:掌握不等式的性质1,2,3.
二、目标和目标解析
1.目标
(1)掌握不等式的基本事实和性质,会利用不等式的性质求出不等式的解集,并能在数轴上表示其解集.
(2)经历不等式性质的探索过程,培养观察和推理能力、体会类比思想,分类讨论思想和数学归纳思想.
(3)用不等式的基本性质解简单的不等式,培养应用意识,发展运算能力.
2.目标解析
(1)学生需要理解不等式的基本事实中数的大小关系与不等式符号的联系.对于不等式的性质,不仅要知道文字表述,更要能通过具体例子进行验证、运用和理解.学生要能够根据给定的不等式,正确运用性质进行变形,逐步求出使不等式成立的未知数的取值范围.在数轴上表示解集,学生要掌握用实心点或空心点表示端点值,以及根据不等号方向确定取值范围在数轴上的表示方法.
(2)在探索不等式的性质时,学生通过观察不同的不等式在进行加、减、乘、除运算后,不等号的变化情况,归纳总结出一般性的性质,培养观察和数学归纳能力.学生在等式性质的基础上,发现不等式性质与等式性质有相似之处,但在乘除负数时又有不同,在体会类比思想的同时加深对不等式性质的理解.分类讨论思想在研究不等式两边乘(或除以)同一个数时体现明显.因为乘(或除以)正数和负数时不等号方向变化不同,所以需要分类讨论,让学生明白不同情况下的处理方式.
(3)学生要能将实际问题中的不等关系抽象为不等式模型,然后运用不等式性质求解,培养应用意识.在解不等式的过程中,学生要熟练运用不等式的性质进行去分母、去括号、移项、合并同类项、系数化为1等运算,逐步提高运算的准确性和速度,发展运算能力.
三、教学问题诊断分析
1.学生对不等式的性质理解困难:
不等式的性质较为抽象,尤其是涉及到乘除负数时不等号方向改变,学生容易与等式性质混淆,难以理解其本质原因.因此在教学过程中,需要通过大量具体数字的例子,让学生自主计算并观察不等号方向的变化,引导学生思考变化原因.同时,利用数轴直观展示数的大小变化与不等号方向的关系,帮助学生理解.
2.求解不等式解集时出错:
在运用不等式的性质求解不等式时,学生可能会在去分母、系数化为1的过程中出现运算错误,或者在处理不等号方向时出错.因此在教学过程中,需要加强对运算步骤的规范训练,每一步变形都要让学生说明依据.通过小组竞赛等形式,让学生相互检查纠错,提高运算的准确性.对于容易出错的乘除负数改变不等号方向的情况,进行专项练习和强调.
基于以上分析,确定本节课的教学难点为:探索并理解不等式的性质3.
四、教学过程设计
(一)复习引入
问题1 直接说出下列不等式的解集.
(1)x+4>10 (2)2x<6 (3)
解:(1)x>6 (2)x<3 (3)直接得出它的解集比较困难,因此要讨论怎样解不等式.
问题2 解一元一次方程的步骤有哪些?解方程的依据是什么?
答:解一元一次方程的步骤有:去分母,去括号,移项,合并同类项,系数化为一.
解方程的依据是:等式的性质.
问题3 你能说说等式有哪些性质吗?
答:等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
(二)合作探究
关于不等式的基本事实
(1)交换不等式两边,不等号的方向改变:如果a>b,那么b<a.
(2)不等关系可以传递:如果a>b,b>c,那么a>c.
借助数轴理解这两个基本事实
探究1 用 “>”或 “<”填空,并观察不等号的方向是否改变,总结其中的规律:
(1)5>3, (2)-1<3,
5+2 > 3+2, -1+4 < 3+4,
5+0 > 3+0, -1+0 < 3+0,
5+(-2) > 3+(-2); -1+(-7) < 3+(-7).
根据发现的规律填空:不等式两边加同一个数,不等号的方向不变.
不等式两边减同一个数,不等号的方向不变.
追问 换一些其他数,验证这个发现.
不等式的性质1
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c>b±c.
探究2 用 “>”或 “<”填空,并观察不等号的方向是否改变,总结其中的规律:
(1)6>2, (2)-2<3,
6×5 > 2×5, -2×4 < 3×4,
6×(-5) < 2×(-5); -2×(-0.5) > 3×(-0.5).
根据发现的规律填空:不等式两边乘同一个正数,不等号的方向不变.
不等式两边乘同一个负数,不等号的方向改变.
不等式两边除以同一个正数,不等号的方向不变.
不等式两边除以同一个负数,不等号的方向改变.
追问 如果不等式两边乘0,结果又如何呢?
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0,那么ac>bc(或 > ).
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,c<0,那么ac<bc(或 < ).
探究3 生活中的不等关系
a≥b或a≤b形式的不等式,具有与前面所说的不等式的性质类似的性质.
若a≥b,则①a±c≥b±c; ②ac≥bc(c>0); ③ac≤bc(c<0).
生活中也有很多不等关系可以用形如a≥b或a≤b的不等式表示.
如果用v(单位:km/h)表示汽车的速度,则v应满足:80≤v≤100.
(三)典例分析
例2 已知a>b,比较下列两个式子的大小,并说明依据.
(1)a+3与b+3; (2)-2a与-2b.
解:(1)因为a>b,所以 a+3>b+3(不等式的性质1).
因为a>b,所以-2a<-2b(不等式的性质3).
例3 利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1; (3)x>50; (4)-4x>3.
借助不等式的性质,将不等式逐步化为x>m或x<m (m为常数) 的形式.
解:(1)根据不等式的性质1,不等式两边加7,不等号的方向不变,所以
x-7+7>26+7,
x>33.
这个不等式的解集在数轴上的表示如图:
(2)根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以
3x-2x<2x+1-2x,
x<1.
这个不等式的解集在数轴上的表示如图:
(3)根据不等式的性质2,不等式两边乘,不等号的方向不变,所以
×x>×50,
x>75.
这个不等式的解集在数轴上的表示如图:
(4)根据不等式的性质3,不等式两边除以-4,不等号的方向改变,所以
<,
x<.
这个不等式的解集在数轴上的表示如图:
问题 一辆汽车在高速公路上匀速行驶,6:00时汽车距前方的A地210 km,汽车要在8:00之前驶过A地,且汽车所行驶道路的最高限速是120 km/h,车速应满足什么条件?
解:设车速是x km/h.从路程上看,就是以x km/h的速度行驶2 h的路程要超过210 km,这个不等关系可以表示为
2x>210
解得 x>105.
因为汽车所行驶道路的最高限速是120 km/h,所以车速应满足105
分析 问题中的不等关系是:已有水的体积与新注入水的体积之和不能超过鱼缸的容积.
解:因为 “已有水的体积+新注入水的体积V≤鱼缸的容积”,所以
10×3.5×1+V≤10×3.5×7,
解得 V≤210.
又由于新注入水的体积V不能是负数,所以V的取值范围是0≤V≤210.
在数轴上表示V的取值范围如图所示.
(四)巩固练习
1. 已知p>q,用 “>”或 “<”填空,并说明依据:
(1)p+ > q+; 不等式的性质1 (2)p-2 > q-2; 不等式的性质1
(3)p+2m > q+2m; 不等式的性质1 (4)-5p < -5q; 不等式的性质3
(5) > ; 不等式的性质2 (6)4p+1 < 4q+1.不等式的性质2和性质1
2. 已知m>3,利用不等式的性质写出下列各式的取值范围:
(1)m+5; (2); (3)-2m; (4)3m-4.
解:(1)m+5>8;不等式的性质1 (2)>;不等式的性质2
(3)-2m<-6;不等式的性质3 (4)3m-4>5.不等式的性质2和性质1
3.已知a>b,用 “<”或 “>”填空,并说明依据:
(1)2a-5 > 2b-5;不等式的性质2,不等式的性质1.
(2)-3.5b+1 > -3.5a+1.不等式的基本事实,不等式的性质3,不等式的性质1.
4. 关于x的不等式的解集在数轴上的表示如图所示,写出相应的解集.
(1)(2)(3)
解:(1)x≥-2 (2)x<3 (3)-1
(1)x+5>-1; (2)4x<3x+5; (3) x ≤ ; (4)-8x>10.
6. 某日北京的最低气温是19 ℃,最高气温是28 ℃,用不等式表示这天的气温t(单位:℃)的变化范围.
解:气温t(单位:℃)的变化范围是19
解:零件长度L的合格尺寸是39.98≤L≤40.02.
8. 用不等式表示下列不等关系,写出解集并在数轴上表示解集:
(1)x的3倍大于1; (2)x与3的和不小于7;
(3)y的小于或等于-2; (4)y的2倍小于y与1的差.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
归纳总结
思考 比较不等式的性质2和性质3,指出它们有什么区别.再比较不等式的性质和等式的性质,它们有什么异同?
答:等式的性质有两条,它们表明了等式两边进行同样的加(减)、乘(除)运算时,相等关系不变.
不等式的性质有三条,它们表明了不等式两边进行同样的加(减)、乘(除)运算时,大小关系有时不变,有时改变. 对于乘法和除法运算,不等式的性质要分两种情况论述.
感受中考
1.(2024 长春)不等关系在生活中广泛存在.如图,a、b分别表示两位同学的身高,c表示台阶的高度.图中两人的对话体现的数学原理是(A)
A.若a>b,则a+c>b+c B.若a>b,b>c,则a>c
C.若a>b,c>0,则ac>bc D.若a>b,c>0,则
2.(2024 苏州)若a>b﹣1,则下列结论一定正确的是(D)
A.a+1<b B.a﹣1<b C.a>b D.a+1>b
3.(2024 内江)不等式3x≥x﹣4的解集是(A)
A.x≥﹣2 B.x≤﹣2 C.x>﹣2 D.x<﹣2
4.(2024 湖北)不等式x+1≥2的解集在数轴上表示正确的是(A)
A. B.
C. D.
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(七)小结梳理
(八)布置作业
1.必做题:习题11.1 第4题,第5题,第6题.
2.探究性作业:习题11.1 第11题,第12题.
五、教学反思
21世纪教育网(www.21cnjy.com)
同课章节目录
