【2025春新教材】人教版七年级下册数学11.2一元一次不等式(第2课时)(教学设计)
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学11.2一元一次不等式(第2课时)(教学设计) |  | |
| 格式 | zip | ||
| 文件大小 | 735.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 13:05:39 | ||
图片预览



文档简介
/ 让教学更有效 高效备课 | 数学学科
11.2.2 一元一次不等式(第2课时) 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第十一章“不等式与不等式组”11.2.2 一元一次不等式(2),内容包括:能够根据具体的数量关系,列出一元一次不等式解决实际问题;掌握列一元一次不等式解决实际问题的基本步骤.
2.内容解析
作为解决实际问题的有力工具,一元一次不等式能帮助学生处理生活中大量涉及不等关系的问题,增强数学应用能力. 列一元一次不等式解决实际问题与列方程解决实际问题有相似之处,同样需要分析题目中的已知量和未知量,但不同的是,此时挖掘的是不等关系. 学生先前列方程的经验,在设未知数和分析数量关系环节能为列不等式提供一定思路,但需引导他们转变思维,关注不等关系的识别.
基于以上分析,确定本节课的教学重点为:能够根据具体的数量关系,列出一元一次不等式解决实际问题.
二、目标和目标解析
1.目标
(1)能够根据具体的数量关系,列出一元一次不等式解决实际问题.
(2)掌握列一元一次不等式解决实际问题的基本步骤.
(3)通过探究实际问题,进一步体会一元一次不等式的应用价值,发展模型观念.
2.目标解析
(1)学生需要掌握一元一次不等式及其解法,更要能在实际情境中依据具体数量关系列出并求解不等式. 这意味着学生不仅能准确辨别式子是否为一元一次不等式,按步骤正确解题,还能在实际问题中敏锐捕捉不等关系,完成从实际到数学模型构建及求解的全过程
(2)学生要全程参与列一元一次不等式解决实际问题的探索. 通过对比一元一次方程与一元一次不等式,自主总结类比方法;在求解不等式和解决实际问题时,深入理解转化过程,学会将现实问题数学化,构建不等式模型并求解,借此提升分析与解决问题的综合能力.
(3)在解不等式及处理实际问题的过程中,学生要逐渐培养应用意识,提升运算能力. 从生活情境中抽象出不等式模型并解决问题,能增强对数学实用性的认知. 反复运算求解与处理实际问题,有助于提高运算准确性和速度,养成严谨认真的学习态度,深刻体会数学对生活实践的指导价值.
三、教学问题诊断分析
从实际问题抽象数学模型需较强分析理解能力,对部分学生颇具挑战. 面对实际问题,学生可能难以快速梳理不等关系列出不等式.
1.在实际应用中,学生容易误解题意,找错不等关系,列出错误的不等式. 因此,课堂上应针对实际应用易错点增加专项练习,剖析常见错误案例,让学生明确错误根源,提升识别与避免错误的能力.
2.教学中多引导学生逐步分析题目中的已知、未知量,寻找不等关系列出不等式. 引导学生结合实际问题背景,详细阐述不等式解的含义,通过具体实例强化理解. 鼓励学生小组合作交流,共同探讨分析解决问题的方法,培养合作与思维能力.
基于以上分析,确定本节课的教学难点为:从实际情境中抽象出数学模型,准确找到不等关系列出一元一次不等式.
四、教学过程设计
(一)复习引入
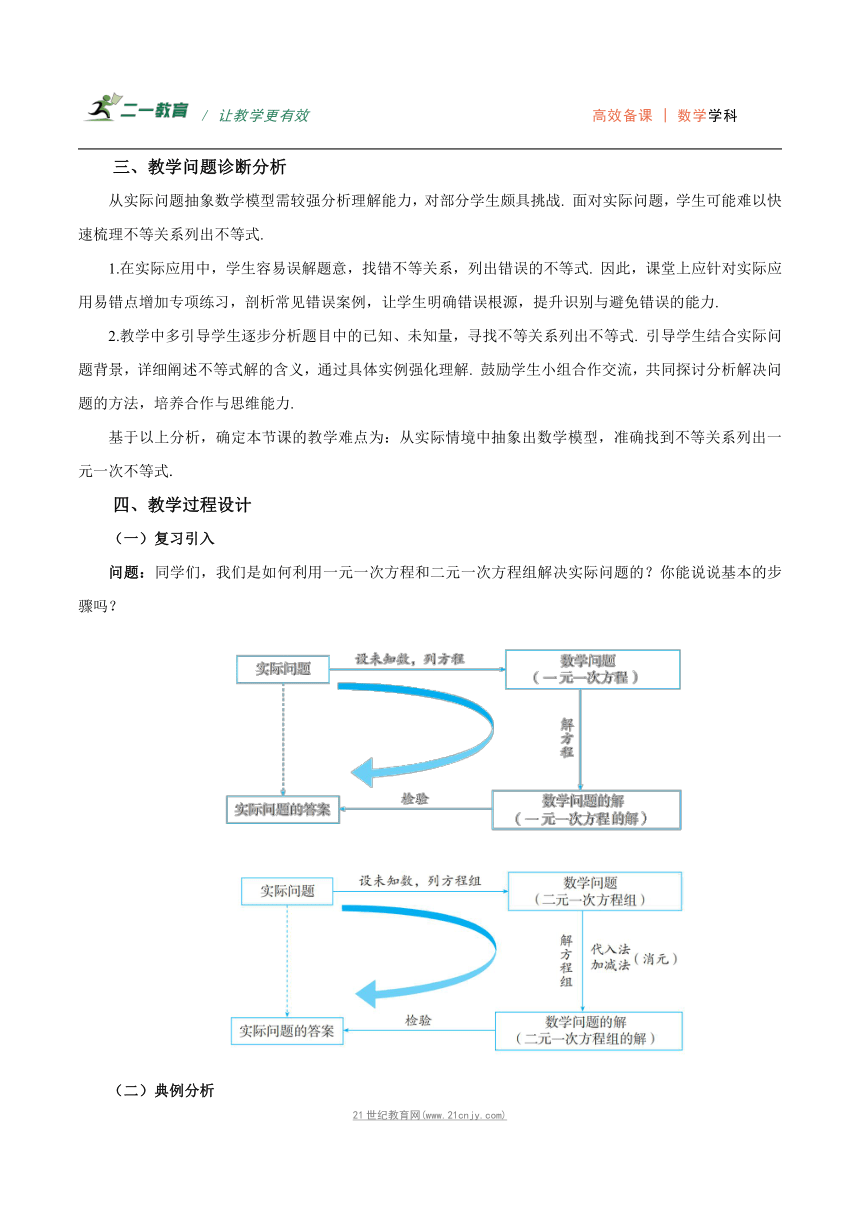
问题:同学们,我们是如何利用一元一次方程和二元一次方程组解决实际问题的?你能说说基本的步骤吗?
(二)典例分析
例2 七年级举办古诗词知识竞赛,共有20道题,每一题答对得10分, 答错或不答都扣5分.如果规定初赛成绩超过90分晋级决赛,那么至少要答对多少道题才能成功晋级?
分析:“初赛成绩超过90分”是问题中蕴含的不等关系,可以根据这个不等关系列出不等式.
解:设初赛答对了x道题. 根据 “初赛成绩超过90分”晋级决赛,列得不等式
10x-5(20-x)>90.
去括号,得 10x-100+5x>90.
移项,合并同类项,得 15x>190.
系数化为1,得 x>12.
由x应为正整数,可得x至少为13.
答:初赛至少要答对13道题才能成功晋级.
“设”中没有描述不等关系的词语,“答”中含有描述不等关系的词语.
例3 某市去年万元地区生产总值能耗为0.320 t标准煤,如果计划使今年万元地区生产总值能耗比去年的下降率不小于5%,那么这个市今年万元地区生产总值能耗至多为多少?
万元地区生产总值能耗是指每万元地区生产总值所消费的能源总量 (折算为标准煤),其下降率是衡量一个地区节能减排成效的重要指标.
分析 “今年万元地区生产总值能耗比去年的下降率不小于5%”是问题中蕴含的不等关系,即
解:设这个市今年万元地区生产总值能耗为x t标准煤.根据题意,列得不等式
去分母,得 0.320-x≥0.320×5%.
移项,合并同类项,得 -x≥-0.304.
系数化为1,得 x≤0.304.
答:这个市今年万元地区生产总值能耗至多为0.304 t标准煤.
例4 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少?
分析:在甲超市购物超过100元后享受优惠,在乙超市购物超过50元后享受优惠.因此,需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
解:设累计购物花费x元.
(1)当累计购物不超过50元,即x≤50时,在甲、乙两超市购物都不享受优惠,而两家超市以同样价格出售同样的商品,因此到两超市购物花费相同.
(2)当累计购物超过50元而不超过100元,即50<x≤100时,在甲超市购物不享受优惠,但在乙超市购物能享受优惠,因此到乙超市购物花费较少.
(3)当累计购物超过100元,即x>100时,在甲、乙两超市购物都能享受优惠.
① 若到甲超市购物花费较少,则
100+0.9(x-100)<50+0.95(x-50). 解得x>150.
即x>150时,到甲超市购物花费较少.
② 若到乙超市购物花费较少,则
100+0.9(x-100)>50+0.95(x-50).解得x<150.
即100<x<150时,到乙超市购物花费较少.
③ 若到两超市购物花费相同,则
100+0.9(x-100)=50+0.95(x-50). 解得x=150.
即x=150时,到甲、乙两超市购物花费相同.
答:当累计购物花费不超过50元或等于150元时,到两家超市购物花费相同;当累计购物超过50元而不到150元时,到乙超市购物花费较少;当累计购物超过150元时,到甲超市购物花费较少.
(三)巩固练习
1. 某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化,准备至少提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设该工程队以后几天内平均每天修路x km.根据题意,列得不等式
(10-2-2)x≥6-1.2.
解得 x≥0.8.
答:该工程队以后几天内平均每天至少要修路0.8 km.
2. 一家商店以每辆340元的进价购入一批自行车共150辆,并以每辆450元的价格销售.两个月后,自行车的销售额已超过这批自行车进货的总费用,这时至少已售出多少辆自行车?
解:设这时已售出x辆自行车.根据题意,列得不等式
450x>340×150.
解得 x>113.
由x应为正整数,可得x至少为114.
答:这时至少已售出114辆自行车.
3.一批苹果的进价是8.55元/kg,销售中估计有5%的苹果正常损耗.商家把售价至少定为多少,才能避免亏本?
解:设苹果的售价是x元/kg.根据题意,列得不等式
(1-5%)x≥8.55.
解得 x≥9.
答:商家把售价至少定为9元/kg.
4.学校打算购买某款笔记本和中性笔作为奖品,奖励给在绘画比赛中获奖的学生.笔记本的价格为16元/个,中性笔的价格为4元/支.如果学校一共要购买100件奖品,总费用不能超过900元,那么学校最多能买多少个笔记本?
解:设学校购买x个笔记本.根据题意,列得不等式
16x+4(100-x)≤900.
解得 x≤41.
由x应为正整数,可得x最大为41.
答:学校最多能买41个笔记本.
5.一家水果店花费10 000元购进了大樱桃和小樱桃各200 kg,计划分别以39元/kg和29元/kg的价格销售,但大樱桃在运输中损耗了20%.若小樱桃的售价不变,为了使获得的总利润不低于预期利润的90%,大樱桃的售价至少要定为每千克多少元?
解:设大樱桃的售价应定为x元/kg.根据题意,列得不等式
200×(1-20%)x+200×29-10 000≥(200×39+200×29-10 000)×90%.
解得 x≥46.5.
答:大樱桃的售价至少要定为每千克46.5元.
6.一条食品包装生产线完成智能化升级后,每个月生产的无菌纸盒包装饮料的数量是原来月均产量的1.7倍.升级后,这条生产线8个月生产的无菌纸盒包装饮料的数量比原来12个月的生产量至少多1 000万盒,这条生产线原来平均每月的产量至少是多少万盒?
解:设这条生产线原来平均每月的产量是x万盒.根据题意,列得不等式
8×1.7x-12x≥1 000.
解得 x≥625.
答:这条生产线原来平均每月的产量至少是625万盒.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
(四)归纳总结
感受中考
1.(2024 山西)为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为540元/个,干粉灭火器的单价为380元/个.若学校购买这两种灭火器的总价不超过21000元,则最多可购买这种型号的水基灭火器多少个?
解:设可购买这种型号的水基灭火器x个,则购买干粉灭火器(50﹣x)个,根据题意得:
540x+380(50﹣x)≤21000,
解得: x≤12.5,
∵x为整数,
∴x取最大值为12,
答:最多可购买这种型号的水基灭火器12个.
2.(2024 哈尔滨)春浩中学在校本课程的实施过程中,计划组织学生编织大、小两种中国结.若编织2个大号中国结和4个小号中国结需用绳20米;若编织1个大号中国结和3个小号中国结需用绳13米.
(1)求编织1个大号中国结和1个小号中国结各需用绳多少米;
(2)春浩中学决定编织以上两种中国结共50个,这两种中国结所用绳长不超过165米,那么该中学最多编织多少个大号中国结?
解:(1)设编织1个大号中国结需用绳x米,编织1个小号中国结需用绳y米,由题意得:
,
解得: ,
答:编织1个大号中国结需用绳4米,编织1个小号中国结需用绳3米;
(2)该中学编织m个大号中国结,则编织(50﹣m)个小号中国结, 由题意得:
4m+3(50﹣m)≤165,
解得: m≤15,
答:该中学最多编织15个大号中国结.
3.(2024 成都)推进中国式现代化,必须坚持不懈夯实农业基础,推进乡村全面振兴.某合作社着力发展乡村水果网络销售,在水果收获的季节,该合作社用17 500元从农户处购进A,B两种水果共1 500kg进行销售,其中A种水果收购单价10元/kg,B种水果收购单价15元/kg.
(1)求A,B两种水果各购进多少千克;
(2)已知A种水果运输和仓储过程中质量损失4%,若合作社计划A种水果至少要获得20%的利润,不计其他费用,求A种水果的最低销售单价.
解:(1)设A种水果购进x千克,B种水果购进y千克,根据题意得:
,
解得: .
答:A种水果购进1000千克,B种水果购进500千克;
(2)设A种水果的销售单价为m元/千克,根据题意得:
1000×(1﹣4%)m﹣10×1000≥10×1000×20%,
解得: m≥12.5,
∴m的最小值为12.5.
答:A种水果的最低销售单价为12.5元/千克.
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(六)小结梳理
(七)布置作业
1.必做题:习题11.2 第5,6题.
2.探究性作业:习题11.2 第10题.
五、教学反思
21世纪教育网(www.21cnjy.com)
11.2.2 一元一次不等式(第2课时) 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第十一章“不等式与不等式组”11.2.2 一元一次不等式(2),内容包括:能够根据具体的数量关系,列出一元一次不等式解决实际问题;掌握列一元一次不等式解决实际问题的基本步骤.
2.内容解析
作为解决实际问题的有力工具,一元一次不等式能帮助学生处理生活中大量涉及不等关系的问题,增强数学应用能力. 列一元一次不等式解决实际问题与列方程解决实际问题有相似之处,同样需要分析题目中的已知量和未知量,但不同的是,此时挖掘的是不等关系. 学生先前列方程的经验,在设未知数和分析数量关系环节能为列不等式提供一定思路,但需引导他们转变思维,关注不等关系的识别.
基于以上分析,确定本节课的教学重点为:能够根据具体的数量关系,列出一元一次不等式解决实际问题.
二、目标和目标解析
1.目标
(1)能够根据具体的数量关系,列出一元一次不等式解决实际问题.
(2)掌握列一元一次不等式解决实际问题的基本步骤.
(3)通过探究实际问题,进一步体会一元一次不等式的应用价值,发展模型观念.
2.目标解析
(1)学生需要掌握一元一次不等式及其解法,更要能在实际情境中依据具体数量关系列出并求解不等式. 这意味着学生不仅能准确辨别式子是否为一元一次不等式,按步骤正确解题,还能在实际问题中敏锐捕捉不等关系,完成从实际到数学模型构建及求解的全过程
(2)学生要全程参与列一元一次不等式解决实际问题的探索. 通过对比一元一次方程与一元一次不等式,自主总结类比方法;在求解不等式和解决实际问题时,深入理解转化过程,学会将现实问题数学化,构建不等式模型并求解,借此提升分析与解决问题的综合能力.
(3)在解不等式及处理实际问题的过程中,学生要逐渐培养应用意识,提升运算能力. 从生活情境中抽象出不等式模型并解决问题,能增强对数学实用性的认知. 反复运算求解与处理实际问题,有助于提高运算准确性和速度,养成严谨认真的学习态度,深刻体会数学对生活实践的指导价值.
三、教学问题诊断分析
从实际问题抽象数学模型需较强分析理解能力,对部分学生颇具挑战. 面对实际问题,学生可能难以快速梳理不等关系列出不等式.
1.在实际应用中,学生容易误解题意,找错不等关系,列出错误的不等式. 因此,课堂上应针对实际应用易错点增加专项练习,剖析常见错误案例,让学生明确错误根源,提升识别与避免错误的能力.
2.教学中多引导学生逐步分析题目中的已知、未知量,寻找不等关系列出不等式. 引导学生结合实际问题背景,详细阐述不等式解的含义,通过具体实例强化理解. 鼓励学生小组合作交流,共同探讨分析解决问题的方法,培养合作与思维能力.
基于以上分析,确定本节课的教学难点为:从实际情境中抽象出数学模型,准确找到不等关系列出一元一次不等式.
四、教学过程设计
(一)复习引入
问题:同学们,我们是如何利用一元一次方程和二元一次方程组解决实际问题的?你能说说基本的步骤吗?
(二)典例分析
例2 七年级举办古诗词知识竞赛,共有20道题,每一题答对得10分, 答错或不答都扣5分.如果规定初赛成绩超过90分晋级决赛,那么至少要答对多少道题才能成功晋级?
分析:“初赛成绩超过90分”是问题中蕴含的不等关系,可以根据这个不等关系列出不等式.
解:设初赛答对了x道题. 根据 “初赛成绩超过90分”晋级决赛,列得不等式
10x-5(20-x)>90.
去括号,得 10x-100+5x>90.
移项,合并同类项,得 15x>190.
系数化为1,得 x>12.
由x应为正整数,可得x至少为13.
答:初赛至少要答对13道题才能成功晋级.
“设”中没有描述不等关系的词语,“答”中含有描述不等关系的词语.
例3 某市去年万元地区生产总值能耗为0.320 t标准煤,如果计划使今年万元地区生产总值能耗比去年的下降率不小于5%,那么这个市今年万元地区生产总值能耗至多为多少?
万元地区生产总值能耗是指每万元地区生产总值所消费的能源总量 (折算为标准煤),其下降率是衡量一个地区节能减排成效的重要指标.
分析 “今年万元地区生产总值能耗比去年的下降率不小于5%”是问题中蕴含的不等关系,即
解:设这个市今年万元地区生产总值能耗为x t标准煤.根据题意,列得不等式
去分母,得 0.320-x≥0.320×5%.
移项,合并同类项,得 -x≥-0.304.
系数化为1,得 x≤0.304.
答:这个市今年万元地区生产总值能耗至多为0.304 t标准煤.
例4 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少?
分析:在甲超市购物超过100元后享受优惠,在乙超市购物超过50元后享受优惠.因此,需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
解:设累计购物花费x元.
(1)当累计购物不超过50元,即x≤50时,在甲、乙两超市购物都不享受优惠,而两家超市以同样价格出售同样的商品,因此到两超市购物花费相同.
(2)当累计购物超过50元而不超过100元,即50<x≤100时,在甲超市购物不享受优惠,但在乙超市购物能享受优惠,因此到乙超市购物花费较少.
(3)当累计购物超过100元,即x>100时,在甲、乙两超市购物都能享受优惠.
① 若到甲超市购物花费较少,则
100+0.9(x-100)<50+0.95(x-50). 解得x>150.
即x>150时,到甲超市购物花费较少.
② 若到乙超市购物花费较少,则
100+0.9(x-100)>50+0.95(x-50).解得x<150.
即100<x<150时,到乙超市购物花费较少.
③ 若到两超市购物花费相同,则
100+0.9(x-100)=50+0.95(x-50). 解得x=150.
即x=150时,到甲、乙两超市购物花费相同.
答:当累计购物花费不超过50元或等于150元时,到两家超市购物花费相同;当累计购物超过50元而不到150元时,到乙超市购物花费较少;当累计购物超过150元时,到甲超市购物花费较少.
(三)巩固练习
1. 某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化,准备至少提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设该工程队以后几天内平均每天修路x km.根据题意,列得不等式
(10-2-2)x≥6-1.2.
解得 x≥0.8.
答:该工程队以后几天内平均每天至少要修路0.8 km.
2. 一家商店以每辆340元的进价购入一批自行车共150辆,并以每辆450元的价格销售.两个月后,自行车的销售额已超过这批自行车进货的总费用,这时至少已售出多少辆自行车?
解:设这时已售出x辆自行车.根据题意,列得不等式
450x>340×150.
解得 x>113.
由x应为正整数,可得x至少为114.
答:这时至少已售出114辆自行车.
3.一批苹果的进价是8.55元/kg,销售中估计有5%的苹果正常损耗.商家把售价至少定为多少,才能避免亏本?
解:设苹果的售价是x元/kg.根据题意,列得不等式
(1-5%)x≥8.55.
解得 x≥9.
答:商家把售价至少定为9元/kg.
4.学校打算购买某款笔记本和中性笔作为奖品,奖励给在绘画比赛中获奖的学生.笔记本的价格为16元/个,中性笔的价格为4元/支.如果学校一共要购买100件奖品,总费用不能超过900元,那么学校最多能买多少个笔记本?
解:设学校购买x个笔记本.根据题意,列得不等式
16x+4(100-x)≤900.
解得 x≤41.
由x应为正整数,可得x最大为41.
答:学校最多能买41个笔记本.
5.一家水果店花费10 000元购进了大樱桃和小樱桃各200 kg,计划分别以39元/kg和29元/kg的价格销售,但大樱桃在运输中损耗了20%.若小樱桃的售价不变,为了使获得的总利润不低于预期利润的90%,大樱桃的售价至少要定为每千克多少元?
解:设大樱桃的售价应定为x元/kg.根据题意,列得不等式
200×(1-20%)x+200×29-10 000≥(200×39+200×29-10 000)×90%.
解得 x≥46.5.
答:大樱桃的售价至少要定为每千克46.5元.
6.一条食品包装生产线完成智能化升级后,每个月生产的无菌纸盒包装饮料的数量是原来月均产量的1.7倍.升级后,这条生产线8个月生产的无菌纸盒包装饮料的数量比原来12个月的生产量至少多1 000万盒,这条生产线原来平均每月的产量至少是多少万盒?
解:设这条生产线原来平均每月的产量是x万盒.根据题意,列得不等式
8×1.7x-12x≥1 000.
解得 x≥625.
答:这条生产线原来平均每月的产量至少是625万盒.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
(四)归纳总结
感受中考
1.(2024 山西)为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为540元/个,干粉灭火器的单价为380元/个.若学校购买这两种灭火器的总价不超过21000元,则最多可购买这种型号的水基灭火器多少个?
解:设可购买这种型号的水基灭火器x个,则购买干粉灭火器(50﹣x)个,根据题意得:
540x+380(50﹣x)≤21000,
解得: x≤12.5,
∵x为整数,
∴x取最大值为12,
答:最多可购买这种型号的水基灭火器12个.
2.(2024 哈尔滨)春浩中学在校本课程的实施过程中,计划组织学生编织大、小两种中国结.若编织2个大号中国结和4个小号中国结需用绳20米;若编织1个大号中国结和3个小号中国结需用绳13米.
(1)求编织1个大号中国结和1个小号中国结各需用绳多少米;
(2)春浩中学决定编织以上两种中国结共50个,这两种中国结所用绳长不超过165米,那么该中学最多编织多少个大号中国结?
解:(1)设编织1个大号中国结需用绳x米,编织1个小号中国结需用绳y米,由题意得:
,
解得: ,
答:编织1个大号中国结需用绳4米,编织1个小号中国结需用绳3米;
(2)该中学编织m个大号中国结,则编织(50﹣m)个小号中国结, 由题意得:
4m+3(50﹣m)≤165,
解得: m≤15,
答:该中学最多编织15个大号中国结.
3.(2024 成都)推进中国式现代化,必须坚持不懈夯实农业基础,推进乡村全面振兴.某合作社着力发展乡村水果网络销售,在水果收获的季节,该合作社用17 500元从农户处购进A,B两种水果共1 500kg进行销售,其中A种水果收购单价10元/kg,B种水果收购单价15元/kg.
(1)求A,B两种水果各购进多少千克;
(2)已知A种水果运输和仓储过程中质量损失4%,若合作社计划A种水果至少要获得20%的利润,不计其他费用,求A种水果的最低销售单价.
解:(1)设A种水果购进x千克,B种水果购进y千克,根据题意得:
,
解得: .
答:A种水果购进1000千克,B种水果购进500千克;
(2)设A种水果的销售单价为m元/千克,根据题意得:
1000×(1﹣4%)m﹣10×1000≥10×1000×20%,
解得: m≥12.5,
∴m的最小值为12.5.
答:A种水果的最低销售单价为12.5元/千克.
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(六)小结梳理
(七)布置作业
1.必做题:习题11.2 第5,6题.
2.探究性作业:习题11.2 第10题.
五、教学反思
21世纪教育网(www.21cnjy.com)
同课章节目录
