第26章反比例函数检测卷(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
第26章反比例函数检测卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.关于反比例函数,下列说法中正确的是( )
A.图象位于第一、三象限 B.图象与坐标轴没有交点
C.图象是一条直线 D.的值随的值增大而减小
2.反比例函数(,)的图象如图所示,点是图象上一点,轴且与轴交于点,点是轴上任意一点,若的面积为,则的值为( )
A. B. C. D.
3.如图,在反比例函数的图象上任取一点,过点作轴交反比例函数的图象于点,是轴负半轴上一点,连接,,则的面积为( )
A.8 B.10 C.14 D.16
4.若点,,都在反比例函数的图象上,若,则,,的大小关系是( )
A. B. C. D.
5.已知反比例函数与一次函数的图象的一个交点的横坐标为,则的值为( )
A. B. C.5 D.3
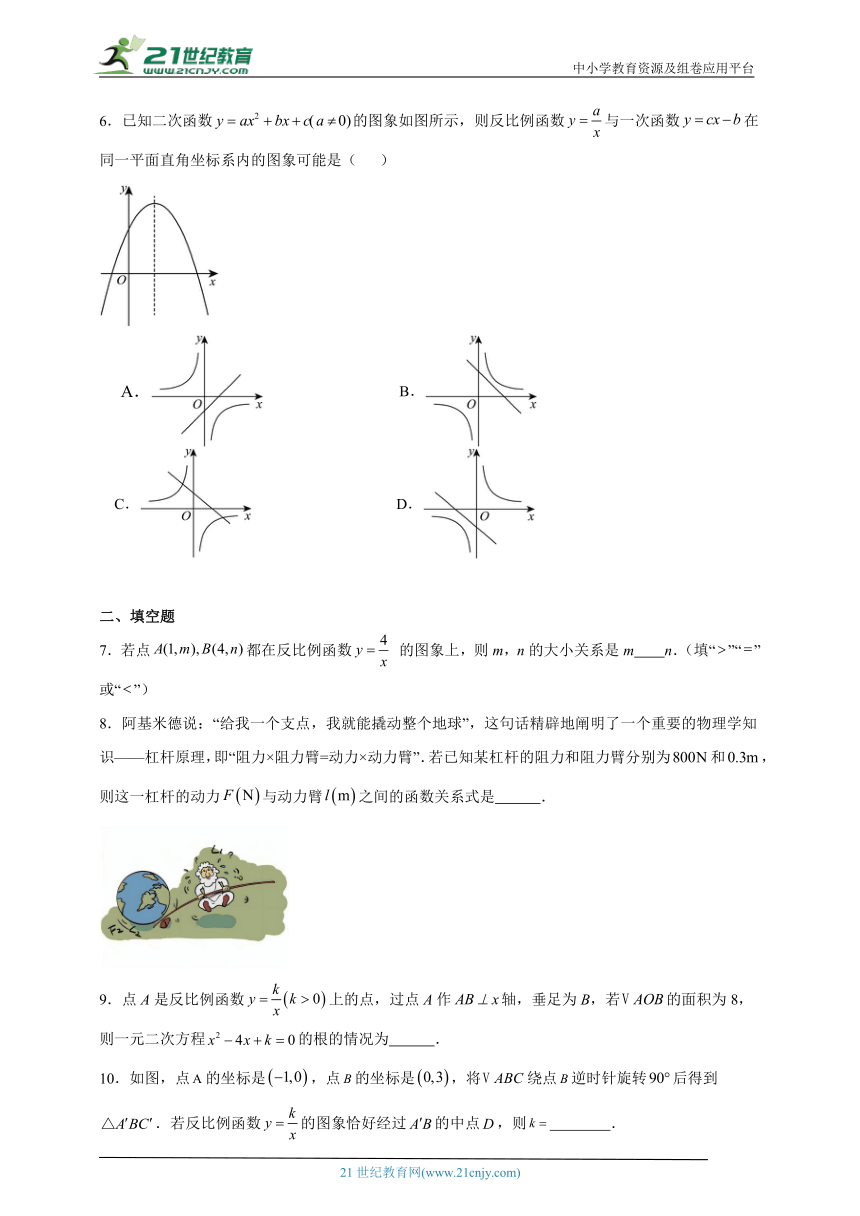
6.已知二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系内的图象可能是( )
B.
C. D.
二、填空题
7.若点都在反比例函数 的图象上,则m,n的大小关系是m n.(填“”“”或“”)
8.阿基米德说:“给我一个支点,我就能撬动整个地球”,这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某杠杆的阻力和阻力臂分别为和,则这一杠杆的动力与动力臂之间的函数关系式是 .
9.点A是反比例函数上的点,过点A作轴,垂足为B,若的面积为8,则一元二次方程的根的情况为 .
10.如图,点的坐标是,点的坐标是,将绕点逆时针旋转后得到.若反比例函数的图象恰好经过的中点,则 .
11.如图,反比例函数的图象经过斜边的中点,且与直角边相交于点.若点的坐标为,则的面积为 .
12.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为 .
三、解答题
13.已知一次函数的图像与反比例函数的图像相交于两点.
(1)求反比例函数与一次函数的表达式,并在图中画出这个一次函数的图像;
(2)根据函数图像,直接写出不等式的解集;
14.如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像相交于点,.
(1)求反比例函数的表达式;
(2)连接、,求的面积.
15.如图,一次函数与反比例函数(k为常数,)的图象在第一象限内交于点,且与轴、轴分别交于B,C两点,已知.
(1)求一次函数和反比例函数的解析式;
(2)若有一点在轴上,且的面积等于6,求点的坐标.
16.手工制品在当今市场上越来越受欢迎.某大学生团队对成本为20元/个的某手工制品进行40天试营销,其销量(个)与销售的时间(天)满足一次函数关系,部分数据如下表:
时间(天) 1 2 3 4 ...
销量(个) 49 48 47 46
团队制定的销售单价(元)与销售的时间(天)关系如下:当时,,当时,.
(1)直接写出关于的函数关系式;
(2)求该团队第天获得的利润关于的函数关系式;
(3)这40天中该团队第几天获得的利润最大?最大利润是多少?
17.如图1,反比例函数与一次函数()的图象交于点,点,一次函数与轴相交于点.
(1)求反比例函数和一次函数的表达式;
(2)连接,,求的面积;
(3)如图2,点是反比例函数图象上点左侧一点,连接,把线段绕点顺时针旋转,点的对应点恰好也落在这个反比例函数的图象上,求点的坐标.
18.如图,在四边形中,,,,,,连接BD,动点P从点A出发沿折线方向运动,动点Q从点C出发沿方向运动,动点P,Q的运动速度均为每秒1个单位长度,当点P到达点D时,P,Q两点时同时停止运动,连接DP,BQ.设运动的时间为x秒,记的面积为,的面积与的面积之比为.
(1)请直接写出,分别关于的函数表达式,并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出函数,的图象,并写出的一条性质;
(3)结合函数图象,请直接写出时的取值范围(结果保留小数点后一位,误差不超过0.2).
《第26章反比例函数检测卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 B C A A A A
1.B
【分析】本题考查了反比例函数的性质,掌握反比例函数的性质是解题的关键.
根据反比例函数解析式得到反比例函数图象是双曲线,经过第二、四象限,与坐标轴没有交点,每个象限随的增大而增大,由此即可求解.
【详解】解:反比例函数,
∵,
∴反比例函数图象是双曲线,经过第二、四象限,与坐标轴没有交点,每个象限随的增大而增大,
∴只有B选项符合题意,
故选:B .
2.C
【分析】本题主要考查了反比例函数的几何意义,掌握反比例函数的几何意义是解题的关键.
连接,由轴,则,然后由反比例函数的几何意义得出,从而求解.
【详解】解:连接,
∵轴,
∴,
∴,
∴,
∵,
∴,
故选:.
3.A
【分析】本题考查反比例函数,熟练利用反比例函数的解析式求点的坐标,运用三角形的面积公式是解答此题的关键.
设点的横坐标为,代入反比例函数中,可得到,由于轴,可得,从而可得的长,知道的底和高,即可得到答案.
【详解】解:设点横坐标为
∵点在上
∴
∵轴
∴
∵在上
∴,则
∴.
故选:A.
4.A
【分析】本题考查了反比例函数的图象与性质,熟练掌握反比例函数的图象与性质是解题关键.先得出,,从而可得,,,再根据反比例函数的增减性可得,由此即可得.
【详解】解:∵,
∴,,
∵点,,都在反比例函数的图象上,
∴,,,
∵反比例函数中的,
∴在每一象限内,随的增大而增大,
又∵点,都在反比例函数的图象上,且,
∴,
∴,
故选:A.
5.A
【分析】本题考查了用待定系数法确定函数的解析式.把代入反比例函数的解析式,即可求得交点坐标,然后利用待定系数法即可求得k的值.
【详解】解:在中,
令,
解得,
则交点坐标是:,
代入,得.
解得.
故选:A.
6.A
【分析】本题主要考查了二次函数图象,一次函数图象,反比例函数图象,首先根据二次函数图象与y轴的交点可得,根据抛物线开口向下可得,由对称轴在y轴右边可得a,b异号,故,再根据反比例函数的性质与一次函数图象与系数的关系画出图象可得答案.
【详解】解:根据二次函数图象与y轴的交点可得,根据抛物线开口向下可得,由对称轴在y轴右边可得a,b异号,故,
则反比例函数的图象在第二,四象限,
一次函数经过第一,二,四象限,
故选:.
7.
【分析】本题考查的是反比例函数图象的性质,利用函数的增减性求解.根据反比例函数的值,判断函数的增减性即可求解.
【详解】解:反比例函数,,
∴函数的图象在一 、三象限,
根据函数性质,函数在一 、三象限,在每一个象限内,随的增大而减小,
,
,
故答案为:.
8.
【分析】本题考查了反比例函数的应用.直接利用阻力×阻力臂=动力×动力臂,进而得出动力F关于动力臂l的函数关系式,从而确定其图象即可.
【详解】解:∵阻力×阻力臂=动力×动力臂,阻力和阻力臂分别为和,
∴动力F和动力臂l之间的函数解析式为,
则,
∴这一杠杆的动力与动力臂之间的函数关系式是,
故答案为:.
9.无实数根
【分析】本题考查了反比例函数系数的几何意义,一次二次方程的根的情况,根据反比例函数系数k的几何意义得到,求得到k的值,再根据一元二次方程根的判别式的正负得出根的情况.
【详解】解:根据题意得,
∵,
∴,
∴一元二次方程为,
∵,
∴方程无实数根,
故答案为:无实数根.
10.
【分析】本题考查旋转的性质,全等三角形性质和判定,待定系数法求反比例函数解析式,解题的关键在于熟练掌握相关知识.过点作于点,结合旋转的性质,证明,结合全等三角形性质得到点的坐标,进而得到点的坐标,最后利用待定系数法求解,即可解题.
【详解】解:过点作于点,
,
由旋转的性质可知,,,
,
,
,
,
点的坐标是,点的坐标是,
,,
,
,
点,
反比例函数的图象恰好经过的中点,
则,
故答案为:.
11.3
【分析】本题考查了反比例函数解析式以及三角形的面积,由斜边的中点得到,再求出反比例函数解析式,再根据垂直得到,最后根据计算即可.
【详解】解:∵点的坐标为,
∴斜边的中点,
把代入得,,解得,
∴反比例函数解析式为
∵,
∴轴,
∴、的横坐标为,
当时,,
∴,
∴,
∴,
故答案为:.
12.
【分析】本题考查了求反比例函数的解析式,熟练掌握待定系数法求函数解析式是解题的关键.设函数解析式为I(),把代入函数解析式求得值即可.
【详解】解:设函数解析式为I(),
把代入函数解析式得,
,
.
故答案为:.
13.(1),,见解析
(2)或
【分析】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式.
(1)待定系数法求出两个函数解析式即可;
(2)根据函数图象直接写出不等式的解集即可.
【详解】(1)解:一次函数的图象与反比例函数的图象相交于,两点,
,解得,.
一次函数的表达式为:,
反比例函数的表达式为:.
图象如图:
(2)解:把代入,得,
,
根据函数图象不等式的解集为:或.
14.(1)
(2)
【分析】本题考查反比例函数与一次函数的交点问题,解题的关键是掌握一次函数、反比例函数的图像与性质.
(1)先将点,代入,求出,,再利用待定系数法求出反比例函数解析式即可;
(2)设一次函数的图像与轴交于点,求出,得到,再用分割法求出的面积即可.
【详解】(1)解:将点,代入得:,,
,,
,,
将代入反比例函数中,得:,
反比例函数的表达式为;
(2)解:连接,如图所示:
设一次函数的图像与轴交于点,
在中,令,则,
,
,
由(1)知,,,
.
15.(1),
(2)点的坐标为或
【分析】(1)由一次函数与轴、轴分别交于B,C两点,得到,得到,把两函数的交点A的坐标分别代入,可得到两函数解析式;
(2)设点的坐标为,利用三角形面积公式得到,然后求出t得到P点坐标.
本题考查了反比例函数与一次函数的交点问题:待定系数法,三角形的面积的计算方法,求出点B坐标是解本题的关键.
【详解】(1)解:一次函数与轴、轴分别交于B,C两点,
.
,
,
一次函数的解析式为;
点在一次函数上,
点.
把点代入,得,
反比例函数的解析式为.
(2)设点的坐标为.
当时,,解得,则点.
的面积等于6,
,
解得或,
点的坐标为或.
16.(1)
(2)
(3)这40天中第21天获得的利润最大,最大利润是725元
【分析】(1)根据表格数据,由待定系数法确定函数关系式即可得到答案;
(2)由团队制定的销售单价(元)与销售的时间(天)关系计算出单个手工制品的利润,再由总利润单个商品利润销量即可得到利润关于的函数关系式;
(3)由(2)中所得的利润关于的函数关系式,分段讨论,由二次函数图象与性质、反比例函数图象与性质求出最值即可得到答案.
【详解】(1)解:设关于的函数关系式为,
将和代入得
,
解得,
关于的函数关系式为;
(2)解:当时,;
当时,
;
关于的函数关系式为;
(3)解:当时,
,
,
∴当时,有最大值,且;
当时,
∵,
随着的增大而减小,
当时,有最大值,且;
,
这40天中第21天获得的利润最大,最大利润是725元.
【点睛】本题考查函数解应用题,涉及一次函数的应用、二次函数的应用及反比例函数的应用、待定系数法求一次函数关系式、求分段函数关系式、二次函数图象与性质求最值、反比例函数图象与性质求最值等知识,熟练掌握函数相关知识是解决问题的关键.
17.(1)一次函数的解析式式为,反比例函数的解析式式为;
(2);
(3)点
【分析】(1)将代入反比例函数的解析式求得m的值,再将代入,再把点A和点B的坐标代入求解即可;
(2)先求出点的坐标为,然后利用即可求解;
(3)过点作轴的平行线,作于点,作于点,设,则,,由旋转的性质得,,证明得,,求出点,然后代入反比例函数解析式即可.
【详解】(1)解:因为点在的图象上,所以.
所以反比例函数的解析式式为,
因为点在的图象上,所以.
因为点,在的图象上,
所以,
所以,
所以一次函数的解析式为.
(2)解:令,则,
则点的坐标为.
所以.
(3)解:如图,过点作轴的平行线,作于点,作于点,
设,
∵点,
∴,.
∵线段绕点顺时针旋转,点的对应点恰好也落在这个反比例函数的图象上,
∴,,
∴,
∴,
∴,
在与中,
,
∴,
∴,,
∴,
∴点.
∵点恰好也落在这个反比例函数的图象上,
∴,
解得:(舍去),,
∴点.
【点睛】本题考查了反比例函数与一次函数的交点问题,旋转的性质,全等三角形的判定与性质,利用待定系数法确定反比例函数与一次函数的解析式,数形结合是解题的关键.
18.(1),
(2)见解析,当时,随的增大而增大
(3)或
【分析】本题主要考查了一次函数与反比例函数综合,勾股定理,掌握一次函数与反比例函数综合应用是解题的关键.
(1)由勾股定理得到,当点P在上时,,
当点P在上时,过点A作于E,根据等面积法求出,则,再求出,,由此可求出;
(2)根据(1)所求画出对应的函数图象,再写出对应函数的性质即可;
(3)求出两函数的交点坐标,根据函数图象找到函数图象在函数图象下方方时自变量的取值范围即可.
【详解】(1)解:∵,
∴
∵,
∴
在中,,,
∴,
如图1,当时,如图1,
∴,即;
当时,如图2,过点A作
∵,
∴;
而
∴,即
综上,;
∵
∴,,
∴;
(2)解:①画的图象:
列表:
x 1 2 3 8
y 2 4 6 0
描点,连线,如图:
画的图象,
列表得,
x 1 2 4 5
y 8 4 2 1.6
描点,连线,如图:
性质:当时,随的增大而增大;
(3)解:联立方程组,
解得,或(舍去)
联立方程组
整理得,,
解得,或,
由函数图象可知,当或时,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第26章反比例函数检测卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.关于反比例函数,下列说法中正确的是( )
A.图象位于第一、三象限 B.图象与坐标轴没有交点
C.图象是一条直线 D.的值随的值增大而减小
2.反比例函数(,)的图象如图所示,点是图象上一点,轴且与轴交于点,点是轴上任意一点,若的面积为,则的值为( )
A. B. C. D.
3.如图,在反比例函数的图象上任取一点,过点作轴交反比例函数的图象于点,是轴负半轴上一点,连接,,则的面积为( )
A.8 B.10 C.14 D.16
4.若点,,都在反比例函数的图象上,若,则,,的大小关系是( )
A. B. C. D.
5.已知反比例函数与一次函数的图象的一个交点的横坐标为,则的值为( )
A. B. C.5 D.3
6.已知二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系内的图象可能是( )
B.
C. D.
二、填空题
7.若点都在反比例函数 的图象上,则m,n的大小关系是m n.(填“”“”或“”)
8.阿基米德说:“给我一个支点,我就能撬动整个地球”,这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某杠杆的阻力和阻力臂分别为和,则这一杠杆的动力与动力臂之间的函数关系式是 .
9.点A是反比例函数上的点,过点A作轴,垂足为B,若的面积为8,则一元二次方程的根的情况为 .
10.如图,点的坐标是,点的坐标是,将绕点逆时针旋转后得到.若反比例函数的图象恰好经过的中点,则 .
11.如图,反比例函数的图象经过斜边的中点,且与直角边相交于点.若点的坐标为,则的面积为 .
12.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为 .
三、解答题
13.已知一次函数的图像与反比例函数的图像相交于两点.
(1)求反比例函数与一次函数的表达式,并在图中画出这个一次函数的图像;
(2)根据函数图像,直接写出不等式的解集;
14.如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像相交于点,.
(1)求反比例函数的表达式;
(2)连接、,求的面积.
15.如图,一次函数与反比例函数(k为常数,)的图象在第一象限内交于点,且与轴、轴分别交于B,C两点,已知.
(1)求一次函数和反比例函数的解析式;
(2)若有一点在轴上,且的面积等于6,求点的坐标.
16.手工制品在当今市场上越来越受欢迎.某大学生团队对成本为20元/个的某手工制品进行40天试营销,其销量(个)与销售的时间(天)满足一次函数关系,部分数据如下表:
时间(天) 1 2 3 4 ...
销量(个) 49 48 47 46
团队制定的销售单价(元)与销售的时间(天)关系如下:当时,,当时,.
(1)直接写出关于的函数关系式;
(2)求该团队第天获得的利润关于的函数关系式;
(3)这40天中该团队第几天获得的利润最大?最大利润是多少?
17.如图1,反比例函数与一次函数()的图象交于点,点,一次函数与轴相交于点.
(1)求反比例函数和一次函数的表达式;
(2)连接,,求的面积;
(3)如图2,点是反比例函数图象上点左侧一点,连接,把线段绕点顺时针旋转,点的对应点恰好也落在这个反比例函数的图象上,求点的坐标.
18.如图,在四边形中,,,,,,连接BD,动点P从点A出发沿折线方向运动,动点Q从点C出发沿方向运动,动点P,Q的运动速度均为每秒1个单位长度,当点P到达点D时,P,Q两点时同时停止运动,连接DP,BQ.设运动的时间为x秒,记的面积为,的面积与的面积之比为.
(1)请直接写出,分别关于的函数表达式,并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出函数,的图象,并写出的一条性质;
(3)结合函数图象,请直接写出时的取值范围(结果保留小数点后一位,误差不超过0.2).
《第26章反比例函数检测卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 B C A A A A
1.B
【分析】本题考查了反比例函数的性质,掌握反比例函数的性质是解题的关键.
根据反比例函数解析式得到反比例函数图象是双曲线,经过第二、四象限,与坐标轴没有交点,每个象限随的增大而增大,由此即可求解.
【详解】解:反比例函数,
∵,
∴反比例函数图象是双曲线,经过第二、四象限,与坐标轴没有交点,每个象限随的增大而增大,
∴只有B选项符合题意,
故选:B .
2.C
【分析】本题主要考查了反比例函数的几何意义,掌握反比例函数的几何意义是解题的关键.
连接,由轴,则,然后由反比例函数的几何意义得出,从而求解.
【详解】解:连接,
∵轴,
∴,
∴,
∴,
∵,
∴,
故选:.
3.A
【分析】本题考查反比例函数,熟练利用反比例函数的解析式求点的坐标,运用三角形的面积公式是解答此题的关键.
设点的横坐标为,代入反比例函数中,可得到,由于轴,可得,从而可得的长,知道的底和高,即可得到答案.
【详解】解:设点横坐标为
∵点在上
∴
∵轴
∴
∵在上
∴,则
∴.
故选:A.
4.A
【分析】本题考查了反比例函数的图象与性质,熟练掌握反比例函数的图象与性质是解题关键.先得出,,从而可得,,,再根据反比例函数的增减性可得,由此即可得.
【详解】解:∵,
∴,,
∵点,,都在反比例函数的图象上,
∴,,,
∵反比例函数中的,
∴在每一象限内,随的增大而增大,
又∵点,都在反比例函数的图象上,且,
∴,
∴,
故选:A.
5.A
【分析】本题考查了用待定系数法确定函数的解析式.把代入反比例函数的解析式,即可求得交点坐标,然后利用待定系数法即可求得k的值.
【详解】解:在中,
令,
解得,
则交点坐标是:,
代入,得.
解得.
故选:A.
6.A
【分析】本题主要考查了二次函数图象,一次函数图象,反比例函数图象,首先根据二次函数图象与y轴的交点可得,根据抛物线开口向下可得,由对称轴在y轴右边可得a,b异号,故,再根据反比例函数的性质与一次函数图象与系数的关系画出图象可得答案.
【详解】解:根据二次函数图象与y轴的交点可得,根据抛物线开口向下可得,由对称轴在y轴右边可得a,b异号,故,
则反比例函数的图象在第二,四象限,
一次函数经过第一,二,四象限,
故选:.
7.
【分析】本题考查的是反比例函数图象的性质,利用函数的增减性求解.根据反比例函数的值,判断函数的增减性即可求解.
【详解】解:反比例函数,,
∴函数的图象在一 、三象限,
根据函数性质,函数在一 、三象限,在每一个象限内,随的增大而减小,
,
,
故答案为:.
8.
【分析】本题考查了反比例函数的应用.直接利用阻力×阻力臂=动力×动力臂,进而得出动力F关于动力臂l的函数关系式,从而确定其图象即可.
【详解】解:∵阻力×阻力臂=动力×动力臂,阻力和阻力臂分别为和,
∴动力F和动力臂l之间的函数解析式为,
则,
∴这一杠杆的动力与动力臂之间的函数关系式是,
故答案为:.
9.无实数根
【分析】本题考查了反比例函数系数的几何意义,一次二次方程的根的情况,根据反比例函数系数k的几何意义得到,求得到k的值,再根据一元二次方程根的判别式的正负得出根的情况.
【详解】解:根据题意得,
∵,
∴,
∴一元二次方程为,
∵,
∴方程无实数根,
故答案为:无实数根.
10.
【分析】本题考查旋转的性质,全等三角形性质和判定,待定系数法求反比例函数解析式,解题的关键在于熟练掌握相关知识.过点作于点,结合旋转的性质,证明,结合全等三角形性质得到点的坐标,进而得到点的坐标,最后利用待定系数法求解,即可解题.
【详解】解:过点作于点,
,
由旋转的性质可知,,,
,
,
,
,
点的坐标是,点的坐标是,
,,
,
,
点,
反比例函数的图象恰好经过的中点,
则,
故答案为:.
11.3
【分析】本题考查了反比例函数解析式以及三角形的面积,由斜边的中点得到,再求出反比例函数解析式,再根据垂直得到,最后根据计算即可.
【详解】解:∵点的坐标为,
∴斜边的中点,
把代入得,,解得,
∴反比例函数解析式为
∵,
∴轴,
∴、的横坐标为,
当时,,
∴,
∴,
∴,
故答案为:.
12.
【分析】本题考查了求反比例函数的解析式,熟练掌握待定系数法求函数解析式是解题的关键.设函数解析式为I(),把代入函数解析式求得值即可.
【详解】解:设函数解析式为I(),
把代入函数解析式得,
,
.
故答案为:.
13.(1),,见解析
(2)或
【分析】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式.
(1)待定系数法求出两个函数解析式即可;
(2)根据函数图象直接写出不等式的解集即可.
【详解】(1)解:一次函数的图象与反比例函数的图象相交于,两点,
,解得,.
一次函数的表达式为:,
反比例函数的表达式为:.
图象如图:
(2)解:把代入,得,
,
根据函数图象不等式的解集为:或.
14.(1)
(2)
【分析】本题考查反比例函数与一次函数的交点问题,解题的关键是掌握一次函数、反比例函数的图像与性质.
(1)先将点,代入,求出,,再利用待定系数法求出反比例函数解析式即可;
(2)设一次函数的图像与轴交于点,求出,得到,再用分割法求出的面积即可.
【详解】(1)解:将点,代入得:,,
,,
,,
将代入反比例函数中,得:,
反比例函数的表达式为;
(2)解:连接,如图所示:
设一次函数的图像与轴交于点,
在中,令,则,
,
,
由(1)知,,,
.
15.(1),
(2)点的坐标为或
【分析】(1)由一次函数与轴、轴分别交于B,C两点,得到,得到,把两函数的交点A的坐标分别代入,可得到两函数解析式;
(2)设点的坐标为,利用三角形面积公式得到,然后求出t得到P点坐标.
本题考查了反比例函数与一次函数的交点问题:待定系数法,三角形的面积的计算方法,求出点B坐标是解本题的关键.
【详解】(1)解:一次函数与轴、轴分别交于B,C两点,
.
,
,
一次函数的解析式为;
点在一次函数上,
点.
把点代入,得,
反比例函数的解析式为.
(2)设点的坐标为.
当时,,解得,则点.
的面积等于6,
,
解得或,
点的坐标为或.
16.(1)
(2)
(3)这40天中第21天获得的利润最大,最大利润是725元
【分析】(1)根据表格数据,由待定系数法确定函数关系式即可得到答案;
(2)由团队制定的销售单价(元)与销售的时间(天)关系计算出单个手工制品的利润,再由总利润单个商品利润销量即可得到利润关于的函数关系式;
(3)由(2)中所得的利润关于的函数关系式,分段讨论,由二次函数图象与性质、反比例函数图象与性质求出最值即可得到答案.
【详解】(1)解:设关于的函数关系式为,
将和代入得
,
解得,
关于的函数关系式为;
(2)解:当时,;
当时,
;
关于的函数关系式为;
(3)解:当时,
,
,
∴当时,有最大值,且;
当时,
∵,
随着的增大而减小,
当时,有最大值,且;
,
这40天中第21天获得的利润最大,最大利润是725元.
【点睛】本题考查函数解应用题,涉及一次函数的应用、二次函数的应用及反比例函数的应用、待定系数法求一次函数关系式、求分段函数关系式、二次函数图象与性质求最值、反比例函数图象与性质求最值等知识,熟练掌握函数相关知识是解决问题的关键.
17.(1)一次函数的解析式式为,反比例函数的解析式式为;
(2);
(3)点
【分析】(1)将代入反比例函数的解析式求得m的值,再将代入,再把点A和点B的坐标代入求解即可;
(2)先求出点的坐标为,然后利用即可求解;
(3)过点作轴的平行线,作于点,作于点,设,则,,由旋转的性质得,,证明得,,求出点,然后代入反比例函数解析式即可.
【详解】(1)解:因为点在的图象上,所以.
所以反比例函数的解析式式为,
因为点在的图象上,所以.
因为点,在的图象上,
所以,
所以,
所以一次函数的解析式为.
(2)解:令,则,
则点的坐标为.
所以.
(3)解:如图,过点作轴的平行线,作于点,作于点,
设,
∵点,
∴,.
∵线段绕点顺时针旋转,点的对应点恰好也落在这个反比例函数的图象上,
∴,,
∴,
∴,
∴,
在与中,
,
∴,
∴,,
∴,
∴点.
∵点恰好也落在这个反比例函数的图象上,
∴,
解得:(舍去),,
∴点.
【点睛】本题考查了反比例函数与一次函数的交点问题,旋转的性质,全等三角形的判定与性质,利用待定系数法确定反比例函数与一次函数的解析式,数形结合是解题的关键.
18.(1),
(2)见解析,当时,随的增大而增大
(3)或
【分析】本题主要考查了一次函数与反比例函数综合,勾股定理,掌握一次函数与反比例函数综合应用是解题的关键.
(1)由勾股定理得到,当点P在上时,,
当点P在上时,过点A作于E,根据等面积法求出,则,再求出,,由此可求出;
(2)根据(1)所求画出对应的函数图象,再写出对应函数的性质即可;
(3)求出两函数的交点坐标,根据函数图象找到函数图象在函数图象下方方时自变量的取值范围即可.
【详解】(1)解:∵,
∴
∵,
∴
在中,,,
∴,
如图1,当时,如图1,
∴,即;
当时,如图2,过点A作
∵,
∴;
而
∴,即
综上,;
∵
∴,,
∴;
(2)解:①画的图象:
列表:
x 1 2 3 8
y 2 4 6 0
描点,连线,如图:
画的图象,
列表得,
x 1 2 4 5
y 8 4 2 1.6
描点,连线,如图:
性质:当时,随的增大而增大;
(3)解:联立方程组,
解得,或(舍去)
联立方程组
整理得,,
解得,或,
由函数图象可知,当或时,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
