第11章解三角形章末检测卷(含解析)-2024-2025学年高一数学下学期苏教版2019必修第二册
文档属性
| 名称 | 第11章解三角形章末检测卷(含解析)-2024-2025学年高一数学下学期苏教版2019必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 07:56:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第11章解三角形章末检测卷-2024-2025学年高一数学下学期苏教版2019必修第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若锐角三角形三边长分别为,则的范围是( )
A. B. C. D.
2.在中,,,则的值为( )
A.2 B.3 C.4 D.5
3.的内角A,B,C的对边分别为a,b,c,若,则为( ).
A.等腰直角三角形 B.等腰三角形或直角三角形
C.直角三角形 D.等边三角形
4.某数学兴趣小组成员为测量某建筑的高度OP,选取了在同一水平面上的A,B,C三处,如图.已知在A,B,C处测得该建筑顶部P的仰角分别为,,,,米,则该建筑的高度( )
A.米 B.米 C.米 D.米
5.已知的内角A,B,C所对应的边分别为a,b,c,若,.则( )
A.2 B.3 C. D.
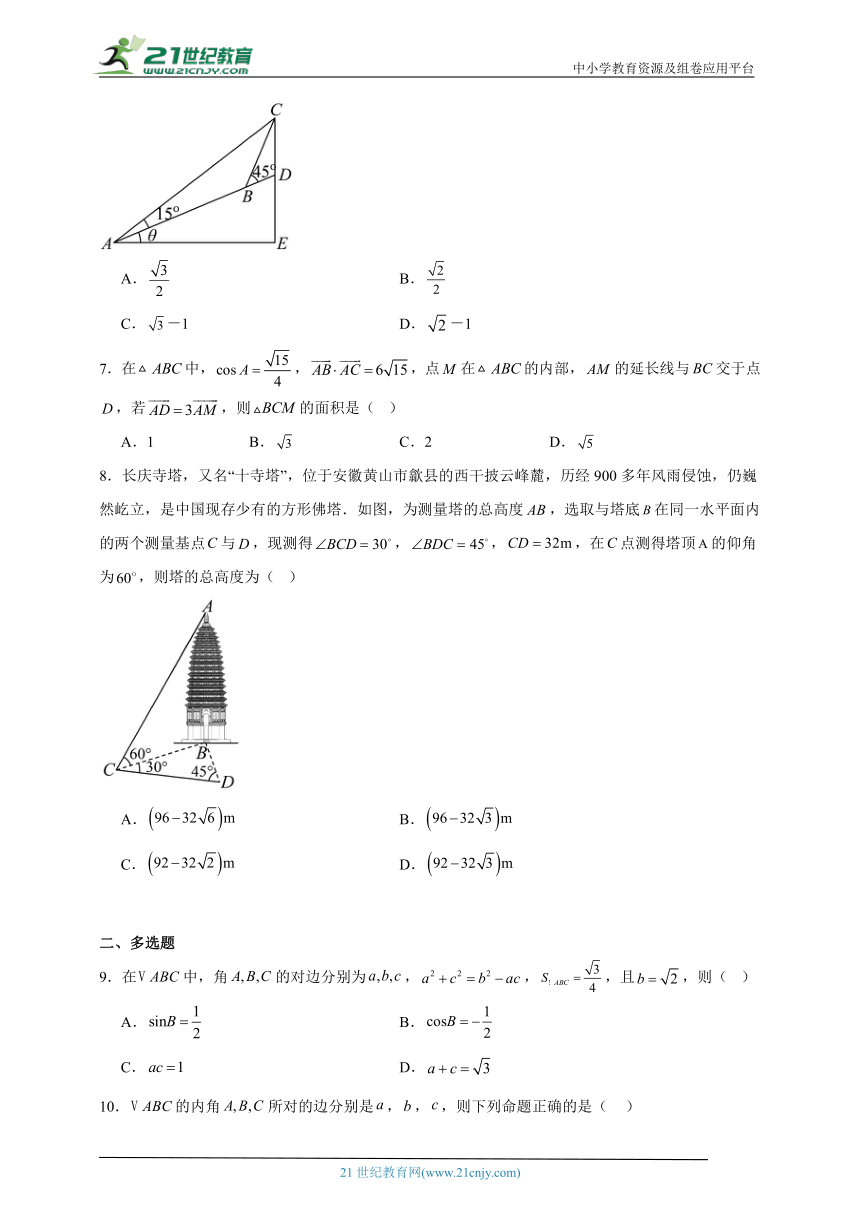
6.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于( )
A. B.
C.-1 D.-1
7.在中,,,点在的内部,的延长线与交于点,若,则的面积是( )
A.1 B. C.2 D.
8.长庆寺塔,又名“十寺塔”,位于安徽黄山市歙县的西干披云峰麓,历经900多年风雨侵蚀,仍巍然屹立,是中国现存少有的方形佛塔.如图,为测量塔的总高度,选取与塔底在同一水平面内的两个测量基点与,现测得,,,在点测得塔顶的仰角为,则塔的总高度为( )
A. B.
C. D.
二、多选题
9.在中,角的对边分别为,,,且,则( )
A. B.
C. D.
10.的内角所对的边分别是,,,则下列命题正确的是( )
A.若,则是钝角三角形
B.若,则是锐角三角形
C.若,则是等腰三角形
D.若,则是直角三角形
11.如图,在平面直角坐标系xAy中,,,,则下列说法正确的有( )
A. B.四边形ABCD的面积为
C.外接圆的周长为 D.
三、填空题
12.在中,内角所对的边分别为,且,则 .
13.在中,内角所对的边分别为,若,,则的面积为 .
14.高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,为山的两侧共线的三点,且与山脚处于同一水平线上,在山顶处测得三点的俯角分别为,计划沿直线开通穿山遂道,现已测得三条线段的长度分别为,则隧道的长度为 .
四、解答题
15.在中,内角所对的边分别为,且.
(1)求;
(2)若的面积为,求.
16.在中,,,分别是角,,所对的边,且满足.
(1)求角的大小;
(2)设向量,向量,且,判断的形状.
17.记锐角三角形的内角,,的对边分别为a,b,c,已知,.
(1)求;
(2)求的最大值.
18.养殖户承包一片靠岸水域,如图为直岸线,,,该承包水域的水面边界是某圆的一段弧,过弧上一点按线段和修建养殖网箱,已知.
(1)求岸线上点与点之间的直线距离;
(2)如果线段上的网箱每千米可获得2万元的经济收益,线段上的网箱每千米可获得4万元的经济收益.记,设两段网箱获得的经济总收益为万元,求的取值范围.
19.设函数.
(1)当时,求函数的最小值并求出对应的;
(2)在中,角的对边分别为,若,且,求周长的取值范围.
《第11章解三角形章末检测卷-2024-2025学年高一数学下学期苏教版2019必修第二册》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B B D C C B BCD AD
题号 11
答案 BC
1.D
【分析】根据题意,分与,结合余弦定理代入计算,即可得到结果.
【详解】由三角形的三边关系可得,解得,
当时,长边所对的角为最大角,由三角形为锐角三角形可得,
,解得,且,则;
当时,长边所对的角为最大角,由三角形为锐角三角形可得,
,解得,且,则;
综上所述,.
故选:D
2.B
【分析】利用余弦定理建立一元二次方程进行求解即可.
【详解】解:中,,
,
即,化简得,
解得或(不合题意,舍去),
,
故选:B.
3.B
【分析】利用余弦定理角化边,然后确定的形状即可.
【详解】因为,
根据余弦定理得,
整理得,
所以或,
所以为等腰三角形或直角三角形,
故选:B.
4.B
【分析】设,由,结合余弦定理可得,求解即可.
【详解】设,则可得,
由,可得B是AC的中点,所以,
而,则,
,中,由余弦定理可得:,
解得:,所以该建筑的高度米.
故选:B.
5.D
【分析】根据已知条件,利用三角形的内角和性质,利用两角差的正弦公式求得角,进而利用正弦定理得解.
【详解】由于三角形的内角和为,即:,已知,所以:,
代入到中,得到:,
展开并化简:,即,
整理得到:,即,
根据正弦定理:,即.
故选:D.
6.C
【分析】在ABC中,由正弦定理得,再在ADC中,由正弦定理得解.
【详解】在ABC中,由正弦定理得,
∴.
在ADC中,,
∴.
故选:C
7.C
【分析】由,,可得,然后由,可得,据此可得答案.
【详解】,因,
则,,得.
又,则,过A,M做BC垂线,垂足为G,F,
则,,又底边相同,
则.
故选:C
8.B
【分析】设,则,在中,利用正弦定理求解.
【详解】设,则,且,
在中,,
∴,即,
解得.
故选:B.
9.BCD
【分析】由已知和余弦定理可求得,进而求得,即可判断A,B;利用三角形面积公式可求得,判断C;由已知和可得,再由可求得,判断D.
【详解】在中,因为,即,
由余弦定理,
又,所以,,故A错误,B正确;
因为,则,所以,故C正确;
因为, ,,
则,
所以,
因为,所以,故D正确.
故答案为:BCD.
10.AD
【分析】由余弦定理易得A项正确;通过举反例,可迅速排除B,C 项,对于D,则先用降幂公式,再用余弦定理,化简后即可判定直角三角形.
【详解】对于A,由余弦定理,,因,故角为钝角,
则是钝角三角形,故A正确;
对于B,若,,显然满足,但此时是直角三角形,故B错误;
对于C,若,显然满足,但此时是直角三角形,故C错误;
对于D,由可得,,即得,,
由余弦定理,,整理得,,故是直角三角形,即D正确.
故选:AD.
11.BC
【分析】利用向量的坐标运算求得即可求解选项A;根据四边形的面积为求解选项B;利用正弦定理求解选项C;利用向量数量积公式求解选项D.
【详解】由题意可得,
所以,故A错误;
过点C作x轴的垂线,设垂足为点E,过点D作x轴的垂线,设垂足为点F,
,
则四边形的面积为
=,故B正确;
因,
在直角三角形中,易得,
设外接圆的半径为R,由正弦定理,,解得,
故外接圆的周长为,故C正确;
因,,
,故D错误.
故选:BC.
12.3
【分析】由余弦定理即可求解;
【详解】由余弦定理知,
即,
整理得,解得.(负值舍去)
故答案为:3
13.
【分析】由正弦定理边角转化得,结合余弦定理可得,利用三角形面积公式可得结果.
【详解】∵,∴由正弦定理得,
∴,即,
∴,即,
由正弦定理得,
∵,∴,
由余弦定理得,得,
∴的面积.
故答案为:.
14.
【分析】过作于,设,则有,从而可得,,在中,可得,从而解得,再由求解即可.
【详解】解:过作于,如图所示:
设,
由题意可知设,
则有,,
所以,
解得,
所以,
在中,,
所以,
所以.
故答案为:
15.(1)
(2).
【分析】(1)对给定式子合理变形,结合余弦定理求解角度即可.
(2)利用三角形面积公式求出,再结合给定条件利用余弦定理建立方程,求解边长即可.
【详解】(1)因为,所以,
整理得,则,
由余弦定理得.
又,解得.
(2)由的面积为,得,
即,解得,
由余弦定理得,
因为,,所以,
即,而,解得.
16.(1)
(2)是以为直角的直角三角形.
【分析】(1)用余弦定理可求角;
(2)根据向量平行的结论,可求角,进而判断的形状.
【详解】(1)由余弦定理:,
又为三角形内角,所以
(2)由(1)可得:,
因为,所以或(因为,不成立,故舍去).
所以,所以.
所以是以为直角的直角三角形.
17.(1)
(2).
【分析】(1)由倍角公式结合正弦定理即可求;
(2)由正弦定理边化角,由为锐角三角形得出的范围,利用正弦型函数性质即可求.
【详解】(1)因为,所以.
又为锐角三角形,故,则.
因为,所以.
又,故.
(2)由正弦定理得,
则,.
由(1)知,则.
所以
,
因为为锐角三角形,
所以,所以,
所以,
所以当时,即时,取得最大值.
18.(1)千米
(2)
【分析】(1)由余弦定理,结合题意,可得答案;
(2)由正弦定理,表示出边,整理利润的三角函数表达式,可得答案.
【详解】(1)在中,由余弦定理,得
即岸线上点A与点之间的直线距离为千米.
(2)在中,设,
,
故有,
,
设两段网箱获得的经济总收益为万元,则
,
故的取值范围为.
19.(1)当时,函数取到最小值为
(2)
【分析】(1)先对函数化简,得到,再利用函数的图像与性质即可求出结果.
(2)利用(1)中条件求出角,再利用余弦定理建立方程,再利用基本不等式和三角形任何两边之和大于第三边,即可求得周长的范围.
【详解】(1)因为
,
因为,所以,
由的图象与性质知,当,即时,函数取到最小值为,
即当时,函数的最小值为,此时.
(2)因为,由(1)得到,
,
即,又在中,则,
所以,即,
又,由余弦定理,得到,
又由基本不等式知,,当且仅当取等号,
所以,则,
又因为,所以,
所以周长的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第11章解三角形章末检测卷-2024-2025学年高一数学下学期苏教版2019必修第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若锐角三角形三边长分别为,则的范围是( )
A. B. C. D.
2.在中,,,则的值为( )
A.2 B.3 C.4 D.5
3.的内角A,B,C的对边分别为a,b,c,若,则为( ).
A.等腰直角三角形 B.等腰三角形或直角三角形
C.直角三角形 D.等边三角形
4.某数学兴趣小组成员为测量某建筑的高度OP,选取了在同一水平面上的A,B,C三处,如图.已知在A,B,C处测得该建筑顶部P的仰角分别为,,,,米,则该建筑的高度( )
A.米 B.米 C.米 D.米
5.已知的内角A,B,C所对应的边分别为a,b,c,若,.则( )
A.2 B.3 C. D.
6.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于( )
A. B.
C.-1 D.-1
7.在中,,,点在的内部,的延长线与交于点,若,则的面积是( )
A.1 B. C.2 D.
8.长庆寺塔,又名“十寺塔”,位于安徽黄山市歙县的西干披云峰麓,历经900多年风雨侵蚀,仍巍然屹立,是中国现存少有的方形佛塔.如图,为测量塔的总高度,选取与塔底在同一水平面内的两个测量基点与,现测得,,,在点测得塔顶的仰角为,则塔的总高度为( )
A. B.
C. D.
二、多选题
9.在中,角的对边分别为,,,且,则( )
A. B.
C. D.
10.的内角所对的边分别是,,,则下列命题正确的是( )
A.若,则是钝角三角形
B.若,则是锐角三角形
C.若,则是等腰三角形
D.若,则是直角三角形
11.如图,在平面直角坐标系xAy中,,,,则下列说法正确的有( )
A. B.四边形ABCD的面积为
C.外接圆的周长为 D.
三、填空题
12.在中,内角所对的边分别为,且,则 .
13.在中,内角所对的边分别为,若,,则的面积为 .
14.高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,为山的两侧共线的三点,且与山脚处于同一水平线上,在山顶处测得三点的俯角分别为,计划沿直线开通穿山遂道,现已测得三条线段的长度分别为,则隧道的长度为 .
四、解答题
15.在中,内角所对的边分别为,且.
(1)求;
(2)若的面积为,求.
16.在中,,,分别是角,,所对的边,且满足.
(1)求角的大小;
(2)设向量,向量,且,判断的形状.
17.记锐角三角形的内角,,的对边分别为a,b,c,已知,.
(1)求;
(2)求的最大值.
18.养殖户承包一片靠岸水域,如图为直岸线,,,该承包水域的水面边界是某圆的一段弧,过弧上一点按线段和修建养殖网箱,已知.
(1)求岸线上点与点之间的直线距离;
(2)如果线段上的网箱每千米可获得2万元的经济收益,线段上的网箱每千米可获得4万元的经济收益.记,设两段网箱获得的经济总收益为万元,求的取值范围.
19.设函数.
(1)当时,求函数的最小值并求出对应的;
(2)在中,角的对边分别为,若,且,求周长的取值范围.
《第11章解三角形章末检测卷-2024-2025学年高一数学下学期苏教版2019必修第二册》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B B D C C B BCD AD
题号 11
答案 BC
1.D
【分析】根据题意,分与,结合余弦定理代入计算,即可得到结果.
【详解】由三角形的三边关系可得,解得,
当时,长边所对的角为最大角,由三角形为锐角三角形可得,
,解得,且,则;
当时,长边所对的角为最大角,由三角形为锐角三角形可得,
,解得,且,则;
综上所述,.
故选:D
2.B
【分析】利用余弦定理建立一元二次方程进行求解即可.
【详解】解:中,,
,
即,化简得,
解得或(不合题意,舍去),
,
故选:B.
3.B
【分析】利用余弦定理角化边,然后确定的形状即可.
【详解】因为,
根据余弦定理得,
整理得,
所以或,
所以为等腰三角形或直角三角形,
故选:B.
4.B
【分析】设,由,结合余弦定理可得,求解即可.
【详解】设,则可得,
由,可得B是AC的中点,所以,
而,则,
,中,由余弦定理可得:,
解得:,所以该建筑的高度米.
故选:B.
5.D
【分析】根据已知条件,利用三角形的内角和性质,利用两角差的正弦公式求得角,进而利用正弦定理得解.
【详解】由于三角形的内角和为,即:,已知,所以:,
代入到中,得到:,
展开并化简:,即,
整理得到:,即,
根据正弦定理:,即.
故选:D.
6.C
【分析】在ABC中,由正弦定理得,再在ADC中,由正弦定理得解.
【详解】在ABC中,由正弦定理得,
∴.
在ADC中,,
∴.
故选:C
7.C
【分析】由,,可得,然后由,可得,据此可得答案.
【详解】,因,
则,,得.
又,则,过A,M做BC垂线,垂足为G,F,
则,,又底边相同,
则.
故选:C
8.B
【分析】设,则,在中,利用正弦定理求解.
【详解】设,则,且,
在中,,
∴,即,
解得.
故选:B.
9.BCD
【分析】由已知和余弦定理可求得,进而求得,即可判断A,B;利用三角形面积公式可求得,判断C;由已知和可得,再由可求得,判断D.
【详解】在中,因为,即,
由余弦定理,
又,所以,,故A错误,B正确;
因为,则,所以,故C正确;
因为, ,,
则,
所以,
因为,所以,故D正确.
故答案为:BCD.
10.AD
【分析】由余弦定理易得A项正确;通过举反例,可迅速排除B,C 项,对于D,则先用降幂公式,再用余弦定理,化简后即可判定直角三角形.
【详解】对于A,由余弦定理,,因,故角为钝角,
则是钝角三角形,故A正确;
对于B,若,,显然满足,但此时是直角三角形,故B错误;
对于C,若,显然满足,但此时是直角三角形,故C错误;
对于D,由可得,,即得,,
由余弦定理,,整理得,,故是直角三角形,即D正确.
故选:AD.
11.BC
【分析】利用向量的坐标运算求得即可求解选项A;根据四边形的面积为求解选项B;利用正弦定理求解选项C;利用向量数量积公式求解选项D.
【详解】由题意可得,
所以,故A错误;
过点C作x轴的垂线,设垂足为点E,过点D作x轴的垂线,设垂足为点F,
,
则四边形的面积为
=,故B正确;
因,
在直角三角形中,易得,
设外接圆的半径为R,由正弦定理,,解得,
故外接圆的周长为,故C正确;
因,,
,故D错误.
故选:BC.
12.3
【分析】由余弦定理即可求解;
【详解】由余弦定理知,
即,
整理得,解得.(负值舍去)
故答案为:3
13.
【分析】由正弦定理边角转化得,结合余弦定理可得,利用三角形面积公式可得结果.
【详解】∵,∴由正弦定理得,
∴,即,
∴,即,
由正弦定理得,
∵,∴,
由余弦定理得,得,
∴的面积.
故答案为:.
14.
【分析】过作于,设,则有,从而可得,,在中,可得,从而解得,再由求解即可.
【详解】解:过作于,如图所示:
设,
由题意可知设,
则有,,
所以,
解得,
所以,
在中,,
所以,
所以.
故答案为:
15.(1)
(2).
【分析】(1)对给定式子合理变形,结合余弦定理求解角度即可.
(2)利用三角形面积公式求出,再结合给定条件利用余弦定理建立方程,求解边长即可.
【详解】(1)因为,所以,
整理得,则,
由余弦定理得.
又,解得.
(2)由的面积为,得,
即,解得,
由余弦定理得,
因为,,所以,
即,而,解得.
16.(1)
(2)是以为直角的直角三角形.
【分析】(1)用余弦定理可求角;
(2)根据向量平行的结论,可求角,进而判断的形状.
【详解】(1)由余弦定理:,
又为三角形内角,所以
(2)由(1)可得:,
因为,所以或(因为,不成立,故舍去).
所以,所以.
所以是以为直角的直角三角形.
17.(1)
(2).
【分析】(1)由倍角公式结合正弦定理即可求;
(2)由正弦定理边化角,由为锐角三角形得出的范围,利用正弦型函数性质即可求.
【详解】(1)因为,所以.
又为锐角三角形,故,则.
因为,所以.
又,故.
(2)由正弦定理得,
则,.
由(1)知,则.
所以
,
因为为锐角三角形,
所以,所以,
所以,
所以当时,即时,取得最大值.
18.(1)千米
(2)
【分析】(1)由余弦定理,结合题意,可得答案;
(2)由正弦定理,表示出边,整理利润的三角函数表达式,可得答案.
【详解】(1)在中,由余弦定理,得
即岸线上点A与点之间的直线距离为千米.
(2)在中,设,
,
故有,
,
设两段网箱获得的经济总收益为万元,则
,
故的取值范围为.
19.(1)当时,函数取到最小值为
(2)
【分析】(1)先对函数化简,得到,再利用函数的图像与性质即可求出结果.
(2)利用(1)中条件求出角,再利用余弦定理建立方程,再利用基本不等式和三角形任何两边之和大于第三边,即可求得周长的范围.
【详解】(1)因为
,
因为,所以,
由的图象与性质知,当,即时,函数取到最小值为,
即当时,函数的最小值为,此时.
(2)因为,由(1)得到,
,
即,又在中,则,
所以,即,
又,由余弦定理,得到,
又由基本不等式知,,当且仅当取等号,
所以,则,
又因为,所以,
所以周长的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
