1.1.1 同底数幂的乘法 课件(共26张PPT)
文档属性
| 名称 | 1.1.1 同底数幂的乘法 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:14:31 | ||
图片预览








文档简介
(共26张PPT)
1.1.1 同底数幂的乘法
第1章 整式的乘法
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解并掌握同底数幂的乘法法则.
2.能够运用同底数幂的乘法法则进行相关计算.
)知识与技能目标
学生能清晰阐述单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘的运算法则,并能准确运用这些法则进行运算。
熟练掌握整式乘法的运算技巧,能够对复杂的整式乘法式子进行化简和求值,确保计算结果的准确性。
(二)过程与方法目标
经历整式乘法运算法则的推导过程,培养学生观察、归纳、类比、推理的能力,提升逻辑思维水平。
引导学生在解决整式乘法问题的过程中,体会从特殊到一般,再从一般到特殊的数学思想方法,增强分析和解决问题的能力。
(三)情感态度与价值观目标
通过自主探究与合作交流,激发学生对数学的探索热情,培养学生勇于创新和团队协作的精神。
让学生感受整式乘法运算的简洁美和规律性,体会数学在实际生活中的广泛应用,增强学习数学的兴趣和自信心。
二、教学重难点
(一)教学重点
深入理解单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘运算法则的推导过程。
熟练运用整式乘法运算法则进行准确计算,包括单项式、多项式的乘法运算及混合运算。
(二)教学难点
理解多项式与多项式相乘时,乘法分配律的运用以及如何准确合并同类项。
灵活运用整式乘法运算法则解决复杂问题,避免在计算过程中出现符号错误和运算顺序错误。
三、教学方法
讲授法:系统讲解整式乘法的概念、运算法则及其推导过程,帮助学生构建清晰的知识框架。
讨论法:组织学生对整式乘法中的重点、难点问题进行讨论,促进学生之间的思维碰撞,加深对知识的理解。
探究法:创设问题情境,引导学生自主探究整式乘法的规律,培养学生的自主学习能力和创新精神。
练习法:通过多样化的练习题,让学生巩固所学的运算法则,提高运算能力和解题技巧,教师及时反馈练习情况,针对错误进行详细讲解。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
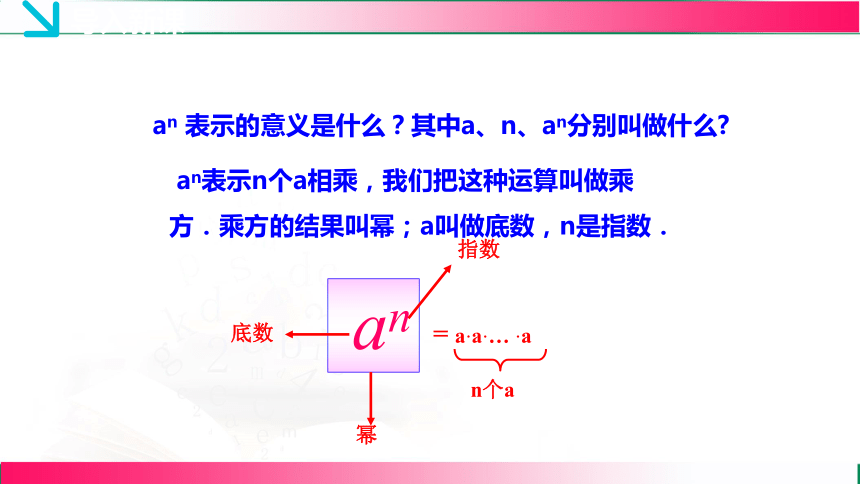
= a·a·… ·a
n个a
an 表示的意义是什么?其中a、n、an分别叫做什么
an
底数
幂
指数
an表示n个a相乘,我们把这种运算叫做乘方.乘方的结果叫幂;a叫做底数,n是指数.
导入新课
探究新知
做一做
22×24=____________; a2·a4=____________;
a3·am=____________(m是正整数).
22×24=
(2×2)×(2×2×2×2)=
26
2个2
4个2
2×2×2×2×2×2=
(2+4)个2
2个a
4个a
(2+4)个a
探究新知
做一做
22×24=____________; a2·a4=____________;
a3·am=____________(m是正整数).
26
a3+m
a6
猜一猜:
比较上述三个式子两端的底数和指数,你会发现什么?
说一说
底数不变,指数相加.
你能将它推导出来吗?
←乘方的意义
←乘法结合律
←乘方的意义
证明:
(m,n都是正整数).
探究新知
总结归纳
于是,我们得到:
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法法则:
正整数)
条件:
结果:
①底数不变
①乘法
②同底数幂
②指数相加
探究新知
例题讲解
例1
计算:
(1)105×103;
(2)x3 · x4.
解: 105×103
= 105+3
= 108.
解: x3 · x4
= x3+4
= x7.
同底数幂相乘,底数不变,指数相加
例题讲解
例2
(1) -a·a3;
解: -a·a3
= (-1)·a1+3
=﹣a4
(2) -y n · y n+1 (n为正整数).
解: -yn · yn+1
= (-1)·yn+n+1
= -y2n+1.
计算:
运用同底数幂乘法法则计算时注意符号问题。
当三个或三个以上的同底数幂相乘时,怎样用公式表示运算的结果呢?
am·an·ak =
(m,n,k都是正整数).
思考
am·an·ak =
( a·a·····a )·(a·a·····a) ·(a·a·····a)
证明:
m个a
n个a
k个a
=a·a·a·····a
(m+n+k)个a
=am+n+k
(m,n,k都是正整数).
同理可知,若三个以上的同底数幂相乘,
底数______,
指数______.
不变
相加
探究新知
例 3
计算:
(2)(-x)×(-x2)×(-x3);
(1) y · y2 · y4 .
解: y · y2 · y4
= (y · y2) · y4
= y7.
= y3 · y4
或: y · y2 · y4
= y1+2+4
= y7.
解: (-x)×(-x2)×(-x3)
=-(x·x2·x3)
=-x6
或: (-x)×(-x2)×(-x3)
=-x1+2+3
= -x6 .
=-(x3·x3)
am·an·ak=am+n+k(m、n、k都是正整数)
例题讲解
1. 教材P3例2(1) 计算 的结果是( )
B
A. B. C. D.
2. 计算 的结果是( )
B
A. B. C. D.
3.[2024·邵阳期末] 计算:
(1) ;
【解】原式 .
(2) .
原式
.
4. [2024·海口校级月考] 当,且 为正整数时,
的值为( )
A
A. 正数 B. 负数
C. 非正数 D. 非负数
【点拨】 .
因为, 为正整数,
所以 .故选A.
5. 已知,,则 的值为
( )
A
A. 15 B.
C. D. 以上都不对
【点拨】因为, ,
所以 ,故选A.
6. 若,则 的值为( )
C
A. 0 B. 1 C. 2 D. 4
【点拨】因为 ,
所以.所以 .
所以 .故选C.
7. 信息技术的存储设备常用B,, ,
等作为存储量的单位.例如,我们常说某手机的容量是
,某个文件的大小是 等,其中
,, ,对于一个存
储量为的 盘,其容量有( )
A
A. B. C. D.
【点拨】因为,, ,
所以 ,故选A.
8. 若 ,则
的值为____.
16
【点拨】因为 ,所以
.
9. 我们知道,同底数幂的乘法法则
为:(其中,, 为正整数),类似
地,我们规定关于任意正整数, 的一种新运算:
,若 ,那么
_________(用含和 的代数式表示,其中
为正整数).
【点拨】因为, ,
所以 ,
,
, ,所以
, .所以原式
.
10. 阅读理解:①根据幂的意义,表示 个
相乘,则;②对于,知道和 可以求
出,我们不妨思考:如果知道,,能否求出 呢?对于
,规定,例如:因为,所以 .
(1)___, ___;
2
3
(2)分别计算,的值,试猜想, ,
之间的等量关系式;
【解】, ,
所以 .
(3)若记,,请用含 的代数
式表示 .
根据题意,得, ,
所以 .
所以 .
课堂小结
同底数幂的乘法
( 都是正整数)
同底数幂相乘,底数不变,指数相加.
法则
扩充法则
当三个或三个以上的同底数幂相乘时,法则仍然适用:
正整数)
谢谢观看!
1.1.1 同底数幂的乘法
第1章 整式的乘法
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解并掌握同底数幂的乘法法则.
2.能够运用同底数幂的乘法法则进行相关计算.
)知识与技能目标
学生能清晰阐述单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘的运算法则,并能准确运用这些法则进行运算。
熟练掌握整式乘法的运算技巧,能够对复杂的整式乘法式子进行化简和求值,确保计算结果的准确性。
(二)过程与方法目标
经历整式乘法运算法则的推导过程,培养学生观察、归纳、类比、推理的能力,提升逻辑思维水平。
引导学生在解决整式乘法问题的过程中,体会从特殊到一般,再从一般到特殊的数学思想方法,增强分析和解决问题的能力。
(三)情感态度与价值观目标
通过自主探究与合作交流,激发学生对数学的探索热情,培养学生勇于创新和团队协作的精神。
让学生感受整式乘法运算的简洁美和规律性,体会数学在实际生活中的广泛应用,增强学习数学的兴趣和自信心。
二、教学重难点
(一)教学重点
深入理解单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘运算法则的推导过程。
熟练运用整式乘法运算法则进行准确计算,包括单项式、多项式的乘法运算及混合运算。
(二)教学难点
理解多项式与多项式相乘时,乘法分配律的运用以及如何准确合并同类项。
灵活运用整式乘法运算法则解决复杂问题,避免在计算过程中出现符号错误和运算顺序错误。
三、教学方法
讲授法:系统讲解整式乘法的概念、运算法则及其推导过程,帮助学生构建清晰的知识框架。
讨论法:组织学生对整式乘法中的重点、难点问题进行讨论,促进学生之间的思维碰撞,加深对知识的理解。
探究法:创设问题情境,引导学生自主探究整式乘法的规律,培养学生的自主学习能力和创新精神。
练习法:通过多样化的练习题,让学生巩固所学的运算法则,提高运算能力和解题技巧,教师及时反馈练习情况,针对错误进行详细讲解。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
= a·a·… ·a
n个a
an 表示的意义是什么?其中a、n、an分别叫做什么
an
底数
幂
指数
an表示n个a相乘,我们把这种运算叫做乘方.乘方的结果叫幂;a叫做底数,n是指数.
导入新课
探究新知
做一做
22×24=____________; a2·a4=____________;
a3·am=____________(m是正整数).
22×24=
(2×2)×(2×2×2×2)=
26
2个2
4个2
2×2×2×2×2×2=
(2+4)个2
2个a
4个a
(2+4)个a
探究新知
做一做
22×24=____________; a2·a4=____________;
a3·am=____________(m是正整数).
26
a3+m
a6
猜一猜:
比较上述三个式子两端的底数和指数,你会发现什么?
说一说
底数不变,指数相加.
你能将它推导出来吗?
←乘方的意义
←乘法结合律
←乘方的意义
证明:
(m,n都是正整数).
探究新知
总结归纳
于是,我们得到:
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法法则:
正整数)
条件:
结果:
①底数不变
①乘法
②同底数幂
②指数相加
探究新知
例题讲解
例1
计算:
(1)105×103;
(2)x3 · x4.
解: 105×103
= 105+3
= 108.
解: x3 · x4
= x3+4
= x7.
同底数幂相乘,底数不变,指数相加
例题讲解
例2
(1) -a·a3;
解: -a·a3
= (-1)·a1+3
=﹣a4
(2) -y n · y n+1 (n为正整数).
解: -yn · yn+1
= (-1)·yn+n+1
= -y2n+1.
计算:
运用同底数幂乘法法则计算时注意符号问题。
当三个或三个以上的同底数幂相乘时,怎样用公式表示运算的结果呢?
am·an·ak =
(m,n,k都是正整数).
思考
am·an·ak =
( a·a·····a )·(a·a·····a) ·(a·a·····a)
证明:
m个a
n个a
k个a
=a·a·a·····a
(m+n+k)个a
=am+n+k
(m,n,k都是正整数).
同理可知,若三个以上的同底数幂相乘,
底数______,
指数______.
不变
相加
探究新知
例 3
计算:
(2)(-x)×(-x2)×(-x3);
(1) y · y2 · y4 .
解: y · y2 · y4
= (y · y2) · y4
= y7.
= y3 · y4
或: y · y2 · y4
= y1+2+4
= y7.
解: (-x)×(-x2)×(-x3)
=-(x·x2·x3)
=-x6
或: (-x)×(-x2)×(-x3)
=-x1+2+3
= -x6 .
=-(x3·x3)
am·an·ak=am+n+k(m、n、k都是正整数)
例题讲解
1. 教材P3例2(1) 计算 的结果是( )
B
A. B. C. D.
2. 计算 的结果是( )
B
A. B. C. D.
3.[2024·邵阳期末] 计算:
(1) ;
【解】原式 .
(2) .
原式
.
4. [2024·海口校级月考] 当,且 为正整数时,
的值为( )
A
A. 正数 B. 负数
C. 非正数 D. 非负数
【点拨】 .
因为, 为正整数,
所以 .故选A.
5. 已知,,则 的值为
( )
A
A. 15 B.
C. D. 以上都不对
【点拨】因为, ,
所以 ,故选A.
6. 若,则 的值为( )
C
A. 0 B. 1 C. 2 D. 4
【点拨】因为 ,
所以.所以 .
所以 .故选C.
7. 信息技术的存储设备常用B,, ,
等作为存储量的单位.例如,我们常说某手机的容量是
,某个文件的大小是 等,其中
,, ,对于一个存
储量为的 盘,其容量有( )
A
A. B. C. D.
【点拨】因为,, ,
所以 ,故选A.
8. 若 ,则
的值为____.
16
【点拨】因为 ,所以
.
9. 我们知道,同底数幂的乘法法则
为:(其中,, 为正整数),类似
地,我们规定关于任意正整数, 的一种新运算:
,若 ,那么
_________(用含和 的代数式表示,其中
为正整数).
【点拨】因为, ,
所以 ,
,
, ,所以
, .所以原式
.
10. 阅读理解:①根据幂的意义,表示 个
相乘,则;②对于,知道和 可以求
出,我们不妨思考:如果知道,,能否求出 呢?对于
,规定,例如:因为,所以 .
(1)___, ___;
2
3
(2)分别计算,的值,试猜想, ,
之间的等量关系式;
【解】, ,
所以 .
(3)若记,,请用含 的代数
式表示 .
根据题意,得, ,
所以 .
所以 .
课堂小结
同底数幂的乘法
( 都是正整数)
同底数幂相乘,底数不变,指数相加.
法则
扩充法则
当三个或三个以上的同底数幂相乘时,法则仍然适用:
正整数)
谢谢观看!
同课章节目录
