1.2.1 平方差公式 课件(共25张PPT)
文档属性
| 名称 | 1.2.1 平方差公式 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:21:14 | ||
图片预览






文档简介
(共25张PPT)
1.2.1 平方差公式
第1章 整式的乘法
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.从代数、几何两个不同的角度理解平方差公式的推导过程.(难点)
2.掌握平方差公式的结构特征并能够运用平方差公式进行计算.(重点)
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
说一说
多项式 x+y 与 x-y 相乘,其积为多少?
(x + y)( x - y ) = x2 - xy + xy -y2= .
x2-y2
多项式 x+y 与 x-y 的乘积,等于多项式 x2-y2
平方差公式:
(x + y )( x - y) =
x2-y2
探究新知
探 究
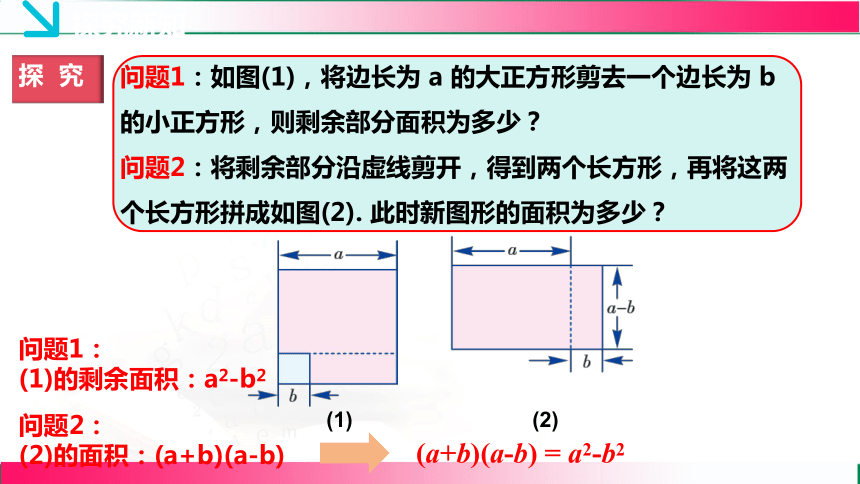
问题1:如图(1),将边长为 a 的大正方形剪去一个边长为 b 的小正方形,则剩余部分面积为多少?
问题2:将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成如图(2). 此时新图形的面积为多少?
(1)
(2)
问题1:
(1)的剩余面积:a2-b2
问题2:
(2)的面积:(a+b)(a-b)
(a+b)(a-b) = a2-b2
总结归纳
平方差公式:
两个数的和与这两个数的差的积等于这两个数的平方差.
(x + y )( x - y) = x2-y2
(x + y )( x - y) =
x2-y2
相同项为x
相反项为y
平方相减
【口诀】
一同一反,平方相减。
探究新知
例题讲解
例1
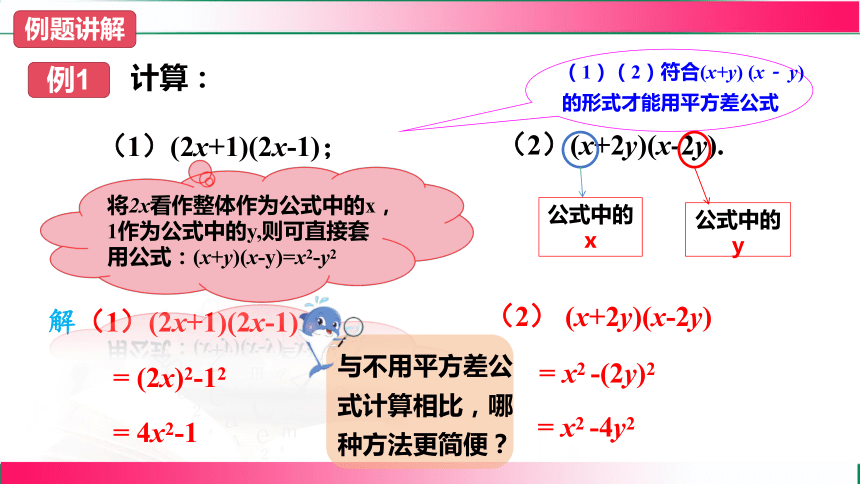
计算:
(1)(2x+1)(2x-1);
(2)(x+2y)(x-2y).
解(1)(2x+1)(2x-1)
= (2x)2-12
= 4x2-1
(1)(2)符合(x+y) (x- y)的形式才能用平方差公式
将2x看作整体作为公式中的x,1作为公式中的y,则可直接套用公式:(x+y)(x-y)=x2-y2
公式中的x
公式中的y
(2) (x+2y)(x-2y)
= x2 -(2y)2
= x2 -4y2
与不用平方差公式计算相比,哪种方法更简便?
例题讲解
例2
运用平方差公式计算:
公式中的x
公式中的y
平方差公式最关键的是找到公式中的x和y, 就可直接套用公式:(x+y)(x-y)=x2-y2
例题讲解
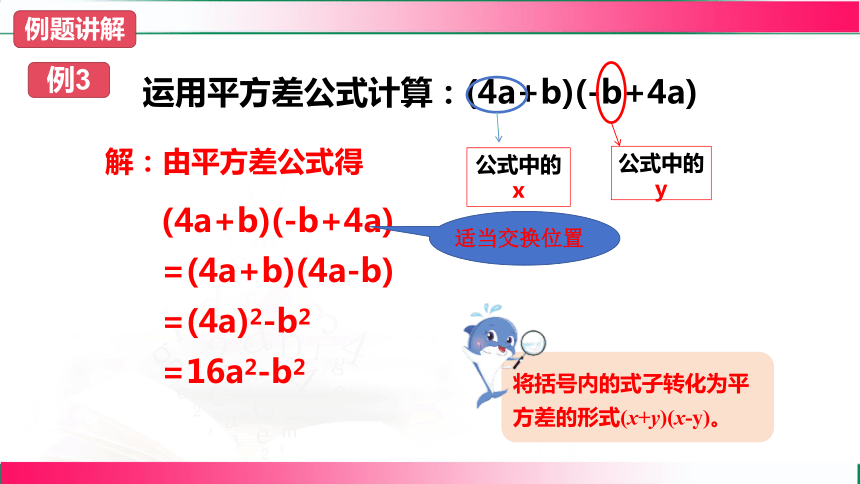
例3
运用平方差公式计算:(4a+b)(-b+4a)
解:由平方差公式得
(4a+b)(-b+4a)
=(4a+b)(4a-b)
=(4a)2-b2
=16a2-b2
将括号内的式子转化为平方差的形式(x+y)(x-y)。
公式中的x
公式中的y
适当交换位置
【平方差公式】
【口诀】
【结构特征总结】
【注意点】
(x+y)(x-y)=x2-y2。
一同一反,平方相减。
①左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
②右边是相同项的平方-相反项的平方。
①公式中的a、b可是具体数,也可以是单项式或多项式;
②对形如两数和与这两数差相乘的计算,都可以用这个公式。
探究新知
计算:1002×998.
解:由平方差公式得
1 002×998
= (1 000+2)(1 000-2)
= 1 0002-22
= 1 000 000-4
= 999 996.
例 4
因此:1002×998=999 996.
运用平方差公式可以简化一些运算。
例题讲解
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
1、利用平方差公式填表。
基础检测
一同一反,平方相减(同的平方减去反的平方)
1. 下列各式中,不能用平方差公式计算的是( )
D
A. B.
C. D.
2. [2024·重庆月考] 若成立,则 的
值为( )
C
A. 3 B. 6 C. 9 D.
3.已知,且,则 ____.
4. 教材P17练习 计算:
(1) ;
【解】原式
.
(2) .
原式
.
5.[2025·广州月考] 已知
,化简 .
【解】
.
6. 若,则 等于
( )
B
A. B. C. 6 D. 8
7. 利用平方差公式计算 ,以下
结果正确的是( )
D
A. B.
C. D.
8. 从前,一位庄园主把一块边长为
的正方形土地租给租户张老汉,第二年,他对张
老汉说:“我把这块地的一边增加 ,相邻的另一边减少
,变成一块长方形的土地继续租给你,租金不变,你也
没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积
( )
A
A. 变小了 B. 变大了
C. 没有变化 D. 无法确定
9. 若,则 ( )
B
A. 4 B. 8 C. D.
10. 如图,大正方形与
小正方形的面积之差是48,则阴影部分
的面积是( )
C
A. 12 B. 18 C. 24 D. 30
【点拨】设大正方形的边长为 ,小正方形的边
长为,所以, .
因为大正方形与小正方形的面积之差是48,所
以.根据题图可得 ,
所以 ,
.
所以阴影部分的面积
故选C.
11. 如果一个正整数可以表示为两个连续奇
数的平方差,那么称该正整数为“和谐数”,如 ,
,则8,16均为“和谐数”.在不超过217的正整数
中,所有的“和谐数”之和为( )
B
A. 3 014 B. 3 024 C. 3 034 D. 3 044
12.已知,则 的值为____.
13.[2024·株洲校级期末] 计算: ________.
25
课堂小结
平方差公式
内容
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(x+y)(x-y)=x2-y2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
注意
谢谢观看!
1.2.1 平方差公式
第1章 整式的乘法
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.从代数、几何两个不同的角度理解平方差公式的推导过程.(难点)
2.掌握平方差公式的结构特征并能够运用平方差公式进行计算.(重点)
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
说一说
多项式 x+y 与 x-y 相乘,其积为多少?
(x + y)( x - y ) = x2 - xy + xy -y2= .
x2-y2
多项式 x+y 与 x-y 的乘积,等于多项式 x2-y2
平方差公式:
(x + y )( x - y) =
x2-y2
探究新知
探 究
问题1:如图(1),将边长为 a 的大正方形剪去一个边长为 b 的小正方形,则剩余部分面积为多少?
问题2:将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成如图(2). 此时新图形的面积为多少?
(1)
(2)
问题1:
(1)的剩余面积:a2-b2
问题2:
(2)的面积:(a+b)(a-b)
(a+b)(a-b) = a2-b2
总结归纳
平方差公式:
两个数的和与这两个数的差的积等于这两个数的平方差.
(x + y )( x - y) = x2-y2
(x + y )( x - y) =
x2-y2
相同项为x
相反项为y
平方相减
【口诀】
一同一反,平方相减。
探究新知
例题讲解
例1
计算:
(1)(2x+1)(2x-1);
(2)(x+2y)(x-2y).
解(1)(2x+1)(2x-1)
= (2x)2-12
= 4x2-1
(1)(2)符合(x+y) (x- y)的形式才能用平方差公式
将2x看作整体作为公式中的x,1作为公式中的y,则可直接套用公式:(x+y)(x-y)=x2-y2
公式中的x
公式中的y
(2) (x+2y)(x-2y)
= x2 -(2y)2
= x2 -4y2
与不用平方差公式计算相比,哪种方法更简便?
例题讲解
例2
运用平方差公式计算:
公式中的x
公式中的y
平方差公式最关键的是找到公式中的x和y, 就可直接套用公式:(x+y)(x-y)=x2-y2
例题讲解
例3
运用平方差公式计算:(4a+b)(-b+4a)
解:由平方差公式得
(4a+b)(-b+4a)
=(4a+b)(4a-b)
=(4a)2-b2
=16a2-b2
将括号内的式子转化为平方差的形式(x+y)(x-y)。
公式中的x
公式中的y
适当交换位置
【平方差公式】
【口诀】
【结构特征总结】
【注意点】
(x+y)(x-y)=x2-y2。
一同一反,平方相减。
①左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
②右边是相同项的平方-相反项的平方。
①公式中的a、b可是具体数,也可以是单项式或多项式;
②对形如两数和与这两数差相乘的计算,都可以用这个公式。
探究新知
计算:1002×998.
解:由平方差公式得
1 002×998
= (1 000+2)(1 000-2)
= 1 0002-22
= 1 000 000-4
= 999 996.
例 4
因此:1002×998=999 996.
运用平方差公式可以简化一些运算。
例题讲解
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
1、利用平方差公式填表。
基础检测
一同一反,平方相减(同的平方减去反的平方)
1. 下列各式中,不能用平方差公式计算的是( )
D
A. B.
C. D.
2. [2024·重庆月考] 若成立,则 的
值为( )
C
A. 3 B. 6 C. 9 D.
3.已知,且,则 ____.
4. 教材P17练习 计算:
(1) ;
【解】原式
.
(2) .
原式
.
5.[2025·广州月考] 已知
,化简 .
【解】
.
6. 若,则 等于
( )
B
A. B. C. 6 D. 8
7. 利用平方差公式计算 ,以下
结果正确的是( )
D
A. B.
C. D.
8. 从前,一位庄园主把一块边长为
的正方形土地租给租户张老汉,第二年,他对张
老汉说:“我把这块地的一边增加 ,相邻的另一边减少
,变成一块长方形的土地继续租给你,租金不变,你也
没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积
( )
A
A. 变小了 B. 变大了
C. 没有变化 D. 无法确定
9. 若,则 ( )
B
A. 4 B. 8 C. D.
10. 如图,大正方形与
小正方形的面积之差是48,则阴影部分
的面积是( )
C
A. 12 B. 18 C. 24 D. 30
【点拨】设大正方形的边长为 ,小正方形的边
长为,所以, .
因为大正方形与小正方形的面积之差是48,所
以.根据题图可得 ,
所以 ,
.
所以阴影部分的面积
故选C.
11. 如果一个正整数可以表示为两个连续奇
数的平方差,那么称该正整数为“和谐数”,如 ,
,则8,16均为“和谐数”.在不超过217的正整数
中,所有的“和谐数”之和为( )
B
A. 3 014 B. 3 024 C. 3 034 D. 3 044
12.已知,则 的值为____.
13.[2024·株洲校级期末] 计算: ________.
25
课堂小结
平方差公式
内容
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(x+y)(x-y)=x2-y2
2.抓住 “一同一反”这一特征,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
注意
谢谢观看!
同课章节目录
