1.2.3 运用乘法公式进行计算和推理 课件(共22张PPT)
文档属性
| 名称 | 1.2.3 运用乘法公式进行计算和推理 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 21:41:59 | ||
图片预览








文档简介
(共22张PPT)
1.2.3 运用乘法公式进行计算和推理
第1章 整式的乘法
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1、灵活运用平方差公式与完全平方公式.(重点)
2、公式变形过程中添括号、变符号等问题.(难点)
学生能清晰阐述单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘的运算法则,并能准确运用这些法则进行运算。
熟练掌握整式乘法的运算技巧,能够对复杂的整式乘法式子进行化简和求值,确保计算结果的准确性。
(二)过程与方法目标
经历整式乘法运算法则的推导过程,培养学生观察、归纳、类比、推理的能力,提升逻辑思维水平。
引导学生在解决整式乘法问题的过程中,体会从特殊到一般,再从一般到特殊的数学思想方法,增强分析和解决问题的能力。
(三)情感态度与价值观目标
通过自主探究与合作交流,激发学生对数学的探索热情,培养学生勇于创新和团队协作的精神。
让学生感受整式乘法运算的简洁美和规律性,体会数学在实际生活中的广泛应用,增强学习数学的兴趣和自信心。
二、教学重难点
(一)教学重点
深入理解单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘运算法则的推导过程。
熟练运用整式乘法运算法则进行准确计算,包括单项式、多项式的乘法运算及混合运算。
(二)教学难点
理解多项式与多项式相乘时,乘法分配律的运用以及如何准确合并同类项。
灵活运用整式乘法运算法则解决复杂问题,避免在计算过程中出现符号错误和运算顺序错误。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
做一做
运用乘法公式计算:(x+1)(x2+1)(x-1)
观察式子有什么结构特点?适合用什么乘法公式?
平方差公式
= x4-1
乘法交换律和结合律
解:原式=(x+1)(x-1)(x2+1)
= (x2-1)(x2 +1 )
平方差公式
发现(x+1)(x-1)符合平方差公式结构特点。
例题讲解
例7
运用乘法公式计算:
(1) (a+b+c)2
(2) (a-b+c) (a+b-c)
怎样才能用完全平方公式呢?
注意:要把(a+b)、c看着一个整体,那么(a+b)就相当于完全平方公式中的x;c就相当于平方差公式中的y.
= [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2+b2+c2+2ab+2ac+2bc
解:(a+b+c)2
完全平方公式
完全平方公式
= a2-(b-c)2
= a2-(b2-2bc+c2)
=a2-b2+2bc-c2
平方差公式
完全平方公式
注意:要把a、(b-c)看着一个整体,那么a就相当于平方差公式中的x,(b-c)就相当于平方差公式中的y. (-b+c)前添负号时,要变号即-(b-c)
解:原式= [a-(b-c)] [a+(b-c)]
例题讲解
例7
运用乘法公式计算:
(1) (a+b+c)2
(2) (a-b+c) (a+b-c)
怎样运用乘法公式计算?
添括号时注意符号的变化。
运用乘法公式计算
例题讲解
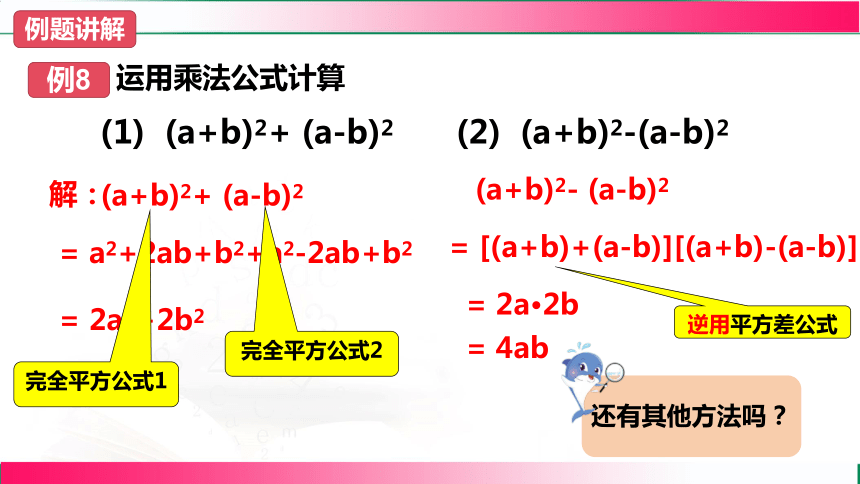
例8
(1) (a+b)2+ (a-b)2
(a+b)2+ (a-b)2
解:
= a2+2ab+b2+a2-2ab+b2
= 2a2+2b2
(2) (a+b)2-(a-b)2
(a+b)2- (a-b)2
= [(a+b)+(a-b)][(a+b)-(a-b)]
= 2a·2b
= 4ab
还有其他方法吗?
完全平方公式2
完全平方公式1
逆用平方差公式
例题讲解
例9
运用乘法公式计算:(x+y)3
(x+y)3
解:
= (x+y) (x+y)2
= (x+y) (x2+2xy+y2)
= x3+2x2y+xy2+yx2+2xy2+y3
= x3+3x2y+3xy2+y3
完全平方公式1
1. [2024·北京朝阳区月考] 已知 ,则代数式
的值为( )
A
A. 4 B. 2 C. 1 D. 0
2.计算:
(1) ;
【解】原式 .
(2) .
原式
.
3.[2024·长沙] 先化简,再求值:
,其中 .
【解】
.
当时,原式 .
4. 已知满足,则
的值是( )
C
A. 512 B. 516 C. 520 D. 1 032
【点拨】因为 ,
所以
.
故选C.
5.已知多项式加上一个单项式 后能成为一个完全平
方式,试写出这个单项式 __________________
(写出一种即可).
(答案不唯一)
6.[2024·厦门第九中学期中] 已知,, , 是从0,
1,2这三个数中取值的一列数,若
,
,则在
,, 中,取值为2的个数为_____.
506
【点拨】因为,, 是从0,1,2这三个数中取
值的一列数,且
,
所以,,中为1的个数是 ,
因为 ,
所以2的个数为 .
7. 【阅读与思考】
下面是小丽同学的数学学习笔记,请仔细阅读并完成相应任务.
两个连续整数平方的平均数与它们平均数的平方之间有什
么关系呢 为了弄清这个问题,我选取两个连续整数7和8进
行探究,为表达方便,设它们平方的平均数为 ,平均数的
平方为,则, ,
发现,且 .我又取了几组连续整
数进行验证,发现的值均为 .
为探究结论的一般性,我设两个连续整数分别为和 ,
进行如下验证: ,
续表
【任务】
(1)请你按小丽的思路完成结论的验证.
【解】设两个连续整数分别为和 ,
则 ,
,
所以 ,
即的值均为 .
(2)按小丽的思路进一步思考:两个连续偶数平方的平均
数与这两个数平均数的平方,它们的差是否也是一个确定的
值?若是,请直接写出这个值;若不是,请说明理由.
是.这个值是1.
【点拨】设两个连续偶数分别为和 ,它们平方的平
均数为,平均数的平方为 ,
则 ,
,
所以 .
所以它们的差也是一个确定的值,这个值是1.
课堂小结
1、乘法公式
平方差公式:
完全平方公式:
(x+y)(x-y)=x2-y2
2、数学思想:
整体思想、转化思想
(x+y)2= x2+2xy+y2
(x-y)2= x2-2xy+y2
运用乘法公式注意事项:
1.要根据具体情况灵活运用乘法公式、幂的运算性质(正用与逆用)。
2.式子变形添括号时注意符号的变化。
谢谢观看!
1.2.3 运用乘法公式进行计算和推理
第1章 整式的乘法
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1、灵活运用平方差公式与完全平方公式.(重点)
2、公式变形过程中添括号、变符号等问题.(难点)
学生能清晰阐述单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘的运算法则,并能准确运用这些法则进行运算。
熟练掌握整式乘法的运算技巧,能够对复杂的整式乘法式子进行化简和求值,确保计算结果的准确性。
(二)过程与方法目标
经历整式乘法运算法则的推导过程,培养学生观察、归纳、类比、推理的能力,提升逻辑思维水平。
引导学生在解决整式乘法问题的过程中,体会从特殊到一般,再从一般到特殊的数学思想方法,增强分析和解决问题的能力。
(三)情感态度与价值观目标
通过自主探究与合作交流,激发学生对数学的探索热情,培养学生勇于创新和团队协作的精神。
让学生感受整式乘法运算的简洁美和规律性,体会数学在实际生活中的广泛应用,增强学习数学的兴趣和自信心。
二、教学重难点
(一)教学重点
深入理解单项式与单项式相乘、单项式与多项式相乘、多项式与多项式相乘运算法则的推导过程。
熟练运用整式乘法运算法则进行准确计算,包括单项式、多项式的乘法运算及混合运算。
(二)教学难点
理解多项式与多项式相乘时,乘法分配律的运用以及如何准确合并同类项。
灵活运用整式乘法运算法则解决复杂问题,避免在计算过程中出现符号错误和运算顺序错误。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
做一做
运用乘法公式计算:(x+1)(x2+1)(x-1)
观察式子有什么结构特点?适合用什么乘法公式?
平方差公式
= x4-1
乘法交换律和结合律
解:原式=(x+1)(x-1)(x2+1)
= (x2-1)(x2 +1 )
平方差公式
发现(x+1)(x-1)符合平方差公式结构特点。
例题讲解
例7
运用乘法公式计算:
(1) (a+b+c)2
(2) (a-b+c) (a+b-c)
怎样才能用完全平方公式呢?
注意:要把(a+b)、c看着一个整体,那么(a+b)就相当于完全平方公式中的x;c就相当于平方差公式中的y.
= [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2+b2+c2+2ab+2ac+2bc
解:(a+b+c)2
完全平方公式
完全平方公式
= a2-(b-c)2
= a2-(b2-2bc+c2)
=a2-b2+2bc-c2
平方差公式
完全平方公式
注意:要把a、(b-c)看着一个整体,那么a就相当于平方差公式中的x,(b-c)就相当于平方差公式中的y. (-b+c)前添负号时,要变号即-(b-c)
解:原式= [a-(b-c)] [a+(b-c)]
例题讲解
例7
运用乘法公式计算:
(1) (a+b+c)2
(2) (a-b+c) (a+b-c)
怎样运用乘法公式计算?
添括号时注意符号的变化。
运用乘法公式计算
例题讲解
例8
(1) (a+b)2+ (a-b)2
(a+b)2+ (a-b)2
解:
= a2+2ab+b2+a2-2ab+b2
= 2a2+2b2
(2) (a+b)2-(a-b)2
(a+b)2- (a-b)2
= [(a+b)+(a-b)][(a+b)-(a-b)]
= 2a·2b
= 4ab
还有其他方法吗?
完全平方公式2
完全平方公式1
逆用平方差公式
例题讲解
例9
运用乘法公式计算:(x+y)3
(x+y)3
解:
= (x+y) (x+y)2
= (x+y) (x2+2xy+y2)
= x3+2x2y+xy2+yx2+2xy2+y3
= x3+3x2y+3xy2+y3
完全平方公式1
1. [2024·北京朝阳区月考] 已知 ,则代数式
的值为( )
A
A. 4 B. 2 C. 1 D. 0
2.计算:
(1) ;
【解】原式 .
(2) .
原式
.
3.[2024·长沙] 先化简,再求值:
,其中 .
【解】
.
当时,原式 .
4. 已知满足,则
的值是( )
C
A. 512 B. 516 C. 520 D. 1 032
【点拨】因为 ,
所以
.
故选C.
5.已知多项式加上一个单项式 后能成为一个完全平
方式,试写出这个单项式 __________________
(写出一种即可).
(答案不唯一)
6.[2024·厦门第九中学期中] 已知,, , 是从0,
1,2这三个数中取值的一列数,若
,
,则在
,, 中,取值为2的个数为_____.
506
【点拨】因为,, 是从0,1,2这三个数中取
值的一列数,且
,
所以,,中为1的个数是 ,
因为 ,
所以2的个数为 .
7. 【阅读与思考】
下面是小丽同学的数学学习笔记,请仔细阅读并完成相应任务.
两个连续整数平方的平均数与它们平均数的平方之间有什
么关系呢 为了弄清这个问题,我选取两个连续整数7和8进
行探究,为表达方便,设它们平方的平均数为 ,平均数的
平方为,则, ,
发现,且 .我又取了几组连续整
数进行验证,发现的值均为 .
为探究结论的一般性,我设两个连续整数分别为和 ,
进行如下验证: ,
续表
【任务】
(1)请你按小丽的思路完成结论的验证.
【解】设两个连续整数分别为和 ,
则 ,
,
所以 ,
即的值均为 .
(2)按小丽的思路进一步思考:两个连续偶数平方的平均
数与这两个数平均数的平方,它们的差是否也是一个确定的
值?若是,请直接写出这个值;若不是,请说明理由.
是.这个值是1.
【点拨】设两个连续偶数分别为和 ,它们平方的平
均数为,平均数的平方为 ,
则 ,
,
所以 .
所以它们的差也是一个确定的值,这个值是1.
课堂小结
1、乘法公式
平方差公式:
完全平方公式:
(x+y)(x-y)=x2-y2
2、数学思想:
整体思想、转化思想
(x+y)2= x2+2xy+y2
(x-y)2= x2-2xy+y2
运用乘法公式注意事项:
1.要根据具体情况灵活运用乘法公式、幂的运算性质(正用与逆用)。
2.式子变形添括号时注意符号的变化。
谢谢观看!
同课章节目录
