3.1 不等式的意义 课件(共23张PPT)
文档属性
| 名称 | 3.1 不等式的意义 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:16:31 | ||
图片预览








文档简介
(共23张PPT)
3.1 不等式的意义
第3章 一元一次不等式(组)
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1、通过实际问题,感受现实生活中存在着大量不等关系.(重点)
2、理解不等式的概念,会判断一个式子是不是不等式.(重点)
学生能够理解一元一次不等式(组)的概念,明确其与一元一次方程的区别与联系。
熟练掌握一元一次不等式(组)的解法,能准确求出其解集,并在数轴上正确表示出来。
过程与方法目标
通过类比一元一次方程的解法探究一元一次不等式(组)的解法,培养学生的类比推理能力和知识迁移能力。
在解决实际问题的过程中,学会将实际问题转化为数学模型,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
通过小组合作学习,培养学生的团队协作精神和交流表达能力。
让学生在探索知识的过程中,体验成功的喜悦,增强学习数学的自信心。
二、教学重难点
教学重点
一元一次不等式(组)的概念和解法。
用数轴表示不等式(组)的解集。
教学难点
不等式基本性质 3 的理解和应用,在不等式两边同时乘以(或除以)同一个负数时,不等号方向要改变。
确定不等式组的解集,尤其是在解复杂的不等式组时,如何准确找到各个不等式解集的公共部分。
三、教学方法
讲授法:通过清晰的讲解,向学生传授一元一次不等式(组)的基本概念、解法步骤和相关理论知识,使学生对新知识有初步的系统认识。
讨论法:组织学生进行小组讨论,针对一元一次不等式(组)与一元一次方程的异同点、不等式组解集的确定方法等问题展开讨论,激发学生的思维,促进学生之间的思想交流与碰撞,培养学生的合作能力和自主探究能力。
练习法:安排适量的练习题,让学生在练习过程中巩固所学的一元一次不等式(组)的解法,及时发现并解决学生在解题过程中出现的问题,提高学生的解题能力和应用知识的能力。
直观演示法:借助数轴,直观地展示不等式(组)的解集,帮助学生更好地理解和掌握解集的概念,突破教学难点。
现实生活中,数量之间存在着相等与不相等的关系.
例如,小华的身高为155cm,小楠的身高为160cm,
160 > 155或155 < 160.
155cm
160cm
对于不相等的关系问题,我们如何用式子来表示它们呢?
则我们可以用不等号“>”或“<”来表示它们的高度之间的关系;
导入新课
探究新知
思 考
(1)如图所示,处于平衡状态的托盘天平的左盘放上一个网球、右盘放上一质量为20 g的砝码后,天平向左倾斜,问网球的质量m g与砝码的质量20 g之间具有怎样的关系?
mg
20g
网球的质量>砝码的质量
m>20
(2)一辆轿车在一条规定车速不低于60 km/h,且不高于100km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km) 与行驶时间t (h) 之间的关系呢?
s ≥ 60t,且 s ≤ 100t
总结归纳
不等式:
用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.
156>155,155<156,m>20, s≥60t, s≤100t,它们有什么共同的特点?
特别提醒:不等号具有方向性,不等号两边的数(或式子)不能随意交换。
探究新知
例题讲解
例1
用不等式表示下列数量关系:
(1)a的5倍大于-7;
(2)a与b的和的一半小于-1;
(3)长、宽分别为b cm,c cm的长方形的面积小于边长为acm的正方形的面积.
5a>-7
bc<a2
解题关键:
1.抓关键词;
2.选准不等号
列不等式,表示出不等关系的步骤有哪些呢?
列不等式
总结归纳
①认真审题,找出问题中要对比的量;
②将要对比的量用代数式表示出来;
③找出问题中表示不等关系的关键词,并用不等号表示出来;
④用不等号将所列的代数式连接起来,列出不等式.
探究新知
例题讲解
例2
已知一支圆珠笔1.5元,签字笔与圆珠笔相比每支贵2元.小华带了50元,买了x支圆珠笔和10支签字笔,请用含x的不等式来表示小华支付的金额与50元之间的关系?
分析
1.x支圆珠笔需要支付_____元, 10支签字笔需要支付___________元,共需要支付__________________元.
1.5x
(2+1.5) ×10
1.5x+(1.5+2) ×10
2.“付50元仍找回若干元”代表支付金额少于50元.
解:1.5x+(1.5+2)×10<50.
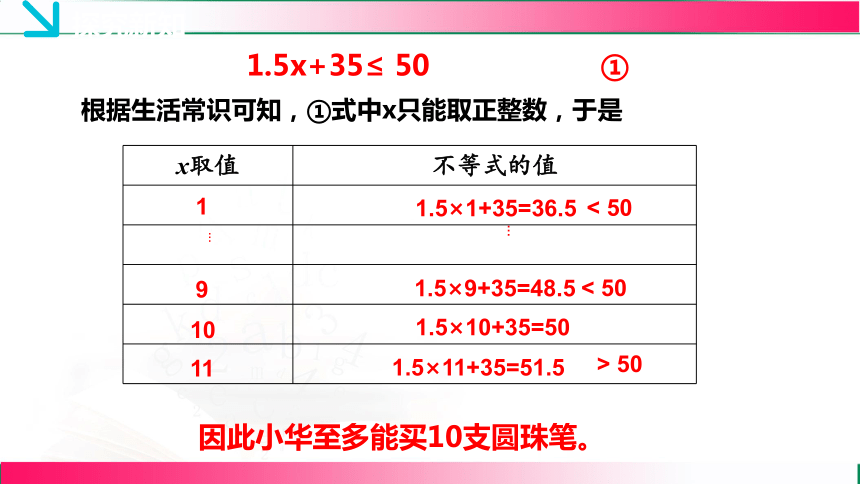
即 1.5x+35≤ 50 ①
x取值 不等式的值
根据生活常识可知,①式中x只能取正整数,于是
1.5×1+35=36.5
1
1.5x+35≤ 50 ①
< 50
···
···
9
10
11
1.5×9+35=48.5
1.5×10+35=50
1.5×11+35=51.5
< 50
> 50
因此小华至多能买10支圆珠笔。
探究新知
例2中,如果小华带了60元,他至多能买多少只圆珠笔?
1.5x+(1.5+2)×10 ≤ 60
解:由于小华带了60元,因此他买x支圆珠笔和10支签字笔支付的金额不超过60元,则有以下不等量关系:
即 1.5x+35≤ 60 ②
探究新知
做一做
x取值 不等式的值
12
···
···
16
17
1.5x+35≤ 60 ②
1.5×12+35=53
1.5×16+35=59
1.5×17+35=60.5
因此小华至多能买16支圆珠笔。
< 60
< 60
> 60
同样,②式中x只能取正整数,于是
探究新知
1. [2024·沈阳和平区月考] 下列式子: ;
;;; .其
中是不等式的有( )
C
A. 5个 B. 4个 C. 3个 D. 2个
2. 某发酵乳的包装瓶上标注“每100克含钙量 毫克”,它
的含义是( )
A
A. 每100克含钙量高于87毫克
B. 每100克含钙量低于87毫克
C. 每100克含钙量不低于87毫克
D. 每100克含钙量不超过87毫克
3. 教材P56例1 用不等式表示:
(1) 的5倍不大于2:_______;
(2) 的一半与5的差是负数:_ __________;
(3)的7倍与 的和不小于15:____________;
(4)三件单价为元的上衣与四条单价为 元的长裤的总价
钱不高于268元:______________.
4. 教材P57例2 小明准备用自己的零花钱买一台价值
1 000元的英语学习机,现在已存100元,如果从现在起每月
存30元,设个月后,他存够了所需钱数,则 应满足的关系
式是( )
B
A. B.
C. D.
5. 小红帮妈妈整理家中药箱,发现其中某瓶药
品的说明书上贴有如图所示的标签,设一次服用药品的剂量
为,则 的取值范围是____________.
6.北斗高精导航能够实时显示当前路口的信号灯颜色及时长,
一辆小车行驶在限速 的路段上,当距离下一路口
时,发现导航显示下一路口的信号灯为绿灯,且剩余
时间为 ,此时导航提示:按照当前时速行驶能通过下一
路口,则小车当前行驶速度 的取值范围是_________
___.
【点拨】 ,
当距离下一路口时,以 的速度通过需要的时间
为 ,
因为要在 内通过,
所以小车的速度至少为 ,
因为导航提示:按照当前时速行驶能通过下一路口,
所以小车当前行驶速度的取值范围是 .
7. 用甲、乙两种原料配制成某种饮料,已知
这两种原料的维生素C的含量及购买这两种原料的价格如下表:
原料 甲种原料 乙种原料
维生素C含量(单位/ ) 500 80
原料价格(元/ ) 16 4
(1)现配制这种饮料 ,要求至少含有4 000单位的维生
素C,试写出所需甲种原料的质量 应满足的不等式;
【解】由题意得 .
(2)如果还要求购买甲、乙两种原料的费用不超过70元,
试写出 应满足的另一个不等式.
由题意得 .
本题运用了建模思想,根据实际问题中的不等关系
建立不等式模型是解题的关键.
课堂小结
2.如何从实际问题中列出不等关系?
1.什么叫不等式?
不等式和等式的联系和区别是什么?
答:把用不等号(>, <, ≥, ≤, ≠)连接而成的式子叫作不等式;
不等式和等式的联系是都是用符号连接的式子;
区别是连接符号不同.
答:读懂题意,并找出表示不等关系的关键词.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
谢谢观看!
3.1 不等式的意义
第3章 一元一次不等式(组)
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1、通过实际问题,感受现实生活中存在着大量不等关系.(重点)
2、理解不等式的概念,会判断一个式子是不是不等式.(重点)
学生能够理解一元一次不等式(组)的概念,明确其与一元一次方程的区别与联系。
熟练掌握一元一次不等式(组)的解法,能准确求出其解集,并在数轴上正确表示出来。
过程与方法目标
通过类比一元一次方程的解法探究一元一次不等式(组)的解法,培养学生的类比推理能力和知识迁移能力。
在解决实际问题的过程中,学会将实际问题转化为数学模型,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
通过小组合作学习,培养学生的团队协作精神和交流表达能力。
让学生在探索知识的过程中,体验成功的喜悦,增强学习数学的自信心。
二、教学重难点
教学重点
一元一次不等式(组)的概念和解法。
用数轴表示不等式(组)的解集。
教学难点
不等式基本性质 3 的理解和应用,在不等式两边同时乘以(或除以)同一个负数时,不等号方向要改变。
确定不等式组的解集,尤其是在解复杂的不等式组时,如何准确找到各个不等式解集的公共部分。
三、教学方法
讲授法:通过清晰的讲解,向学生传授一元一次不等式(组)的基本概念、解法步骤和相关理论知识,使学生对新知识有初步的系统认识。
讨论法:组织学生进行小组讨论,针对一元一次不等式(组)与一元一次方程的异同点、不等式组解集的确定方法等问题展开讨论,激发学生的思维,促进学生之间的思想交流与碰撞,培养学生的合作能力和自主探究能力。
练习法:安排适量的练习题,让学生在练习过程中巩固所学的一元一次不等式(组)的解法,及时发现并解决学生在解题过程中出现的问题,提高学生的解题能力和应用知识的能力。
直观演示法:借助数轴,直观地展示不等式(组)的解集,帮助学生更好地理解和掌握解集的概念,突破教学难点。
现实生活中,数量之间存在着相等与不相等的关系.
例如,小华的身高为155cm,小楠的身高为160cm,
160 > 155或155 < 160.
155cm
160cm
对于不相等的关系问题,我们如何用式子来表示它们呢?
则我们可以用不等号“>”或“<”来表示它们的高度之间的关系;
导入新课
探究新知
思 考
(1)如图所示,处于平衡状态的托盘天平的左盘放上一个网球、右盘放上一质量为20 g的砝码后,天平向左倾斜,问网球的质量m g与砝码的质量20 g之间具有怎样的关系?
mg
20g
网球的质量>砝码的质量
m>20
(2)一辆轿车在一条规定车速不低于60 km/h,且不高于100km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km) 与行驶时间t (h) 之间的关系呢?
s ≥ 60t,且 s ≤ 100t
总结归纳
不等式:
用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.
156>155,155<156,m>20, s≥60t, s≤100t,它们有什么共同的特点?
特别提醒:不等号具有方向性,不等号两边的数(或式子)不能随意交换。
探究新知
例题讲解
例1
用不等式表示下列数量关系:
(1)a的5倍大于-7;
(2)a与b的和的一半小于-1;
(3)长、宽分别为b cm,c cm的长方形的面积小于边长为acm的正方形的面积.
5a>-7
bc<a2
解题关键:
1.抓关键词;
2.选准不等号
列不等式,表示出不等关系的步骤有哪些呢?
列不等式
总结归纳
①认真审题,找出问题中要对比的量;
②将要对比的量用代数式表示出来;
③找出问题中表示不等关系的关键词,并用不等号表示出来;
④用不等号将所列的代数式连接起来,列出不等式.
探究新知
例题讲解
例2
已知一支圆珠笔1.5元,签字笔与圆珠笔相比每支贵2元.小华带了50元,买了x支圆珠笔和10支签字笔,请用含x的不等式来表示小华支付的金额与50元之间的关系?
分析
1.x支圆珠笔需要支付_____元, 10支签字笔需要支付___________元,共需要支付__________________元.
1.5x
(2+1.5) ×10
1.5x+(1.5+2) ×10
2.“付50元仍找回若干元”代表支付金额少于50元.
解:1.5x+(1.5+2)×10<50.
即 1.5x+35≤ 50 ①
x取值 不等式的值
根据生活常识可知,①式中x只能取正整数,于是
1.5×1+35=36.5
1
1.5x+35≤ 50 ①
< 50
···
···
9
10
11
1.5×9+35=48.5
1.5×10+35=50
1.5×11+35=51.5
< 50
> 50
因此小华至多能买10支圆珠笔。
探究新知
例2中,如果小华带了60元,他至多能买多少只圆珠笔?
1.5x+(1.5+2)×10 ≤ 60
解:由于小华带了60元,因此他买x支圆珠笔和10支签字笔支付的金额不超过60元,则有以下不等量关系:
即 1.5x+35≤ 60 ②
探究新知
做一做
x取值 不等式的值
12
···
···
16
17
1.5x+35≤ 60 ②
1.5×12+35=53
1.5×16+35=59
1.5×17+35=60.5
因此小华至多能买16支圆珠笔。
< 60
< 60
> 60
同样,②式中x只能取正整数,于是
探究新知
1. [2024·沈阳和平区月考] 下列式子: ;
;;; .其
中是不等式的有( )
C
A. 5个 B. 4个 C. 3个 D. 2个
2. 某发酵乳的包装瓶上标注“每100克含钙量 毫克”,它
的含义是( )
A
A. 每100克含钙量高于87毫克
B. 每100克含钙量低于87毫克
C. 每100克含钙量不低于87毫克
D. 每100克含钙量不超过87毫克
3. 教材P56例1 用不等式表示:
(1) 的5倍不大于2:_______;
(2) 的一半与5的差是负数:_ __________;
(3)的7倍与 的和不小于15:____________;
(4)三件单价为元的上衣与四条单价为 元的长裤的总价
钱不高于268元:______________.
4. 教材P57例2 小明准备用自己的零花钱买一台价值
1 000元的英语学习机,现在已存100元,如果从现在起每月
存30元,设个月后,他存够了所需钱数,则 应满足的关系
式是( )
B
A. B.
C. D.
5. 小红帮妈妈整理家中药箱,发现其中某瓶药
品的说明书上贴有如图所示的标签,设一次服用药品的剂量
为,则 的取值范围是____________.
6.北斗高精导航能够实时显示当前路口的信号灯颜色及时长,
一辆小车行驶在限速 的路段上,当距离下一路口
时,发现导航显示下一路口的信号灯为绿灯,且剩余
时间为 ,此时导航提示:按照当前时速行驶能通过下一
路口,则小车当前行驶速度 的取值范围是_________
___.
【点拨】 ,
当距离下一路口时,以 的速度通过需要的时间
为 ,
因为要在 内通过,
所以小车的速度至少为 ,
因为导航提示:按照当前时速行驶能通过下一路口,
所以小车当前行驶速度的取值范围是 .
7. 用甲、乙两种原料配制成某种饮料,已知
这两种原料的维生素C的含量及购买这两种原料的价格如下表:
原料 甲种原料 乙种原料
维生素C含量(单位/ ) 500 80
原料价格(元/ ) 16 4
(1)现配制这种饮料 ,要求至少含有4 000单位的维生
素C,试写出所需甲种原料的质量 应满足的不等式;
【解】由题意得 .
(2)如果还要求购买甲、乙两种原料的费用不超过70元,
试写出 应满足的另一个不等式.
由题意得 .
本题运用了建模思想,根据实际问题中的不等关系
建立不等式模型是解题的关键.
课堂小结
2.如何从实际问题中列出不等关系?
1.什么叫不等式?
不等式和等式的联系和区别是什么?
答:把用不等号(>, <, ≥, ≤, ≠)连接而成的式子叫作不等式;
不等式和等式的联系是都是用符号连接的式子;
区别是连接符号不同.
答:读懂题意,并找出表示不等关系的关键词.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
谢谢观看!
同课章节目录
