3.4 一元一次不等式的应用 课件(共28张PPT)
文档属性
| 名称 | 3.4 一元一次不等式的应用 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 21:40:05 | ||
图片预览








文档简介
(共28张PPT)
3.4 一元一次不等式的应用
第3章 一元一次不等式(组)
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.掌握解一元一次不等式的步骤,会用一元一次不等式解简单的实际问题; (重点)
2.寻找实际问题中的不等关系,建立数学模型
(难点)
学生能够理解一元一次不等式(组)的概念,明确其与一元一次方程的区别与联系。
熟练掌握一元一次不等式(组)的解法,能准确求出其解集,并在数轴上正确表示出来。
过程与方法目标
通过类比一元一次方程的解法探究一元一次不等式(组)的解法,培养学生的类比推理能力和知识迁移能力。
在解决实际问题的过程中,学会将实际问题转化为数学模型,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
通过小组合作学习,培养学生的团队协作精神和交流表达能力。
让学生在探索知识的过程中,体验成功的喜悦,增强学习数学的自信心。
二、教学重难点
教学重点
一元一次不等式(组)的概念和解法。
用数轴表示不等式(组)的解集。
教学难点
不等式基本性质 3 的理解和应用,在不等式两边同时乘以(或除以)同一个负数时,不等号方向要改变。
确定不等式组的解集,尤其是在解复杂的不等式组时,如何准确找到各个不等式解集的公共部分。
三、教学方法
讲授法:通过清晰的讲解,向学生传授一元一次不等式(组)的基本概念、解法步骤和相关理论知识,使学生对新知识有初步的系统认识。
讨论法:组织学生进行小组讨论,针对一元一次不等式(组)与一元一次方程的异同点、不等式组解集的确定方法等问题展开讨论,激发学生的思维,促进学生之间的思想交流与碰撞,培养学生的合作能力和自主探究能力。
练习法:安排适量的练习题,让学生在练习过程中巩固所学的一元一次不等式(组)的解法,及时发现并解决学生在解题过程中出现的问题,提高学生的解题能力和应用知识的能力。
直观演示法:借助数轴,直观地展示不等式(组)的解集,帮助学生更好地理解和掌握解集的概念,突破教学难点。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
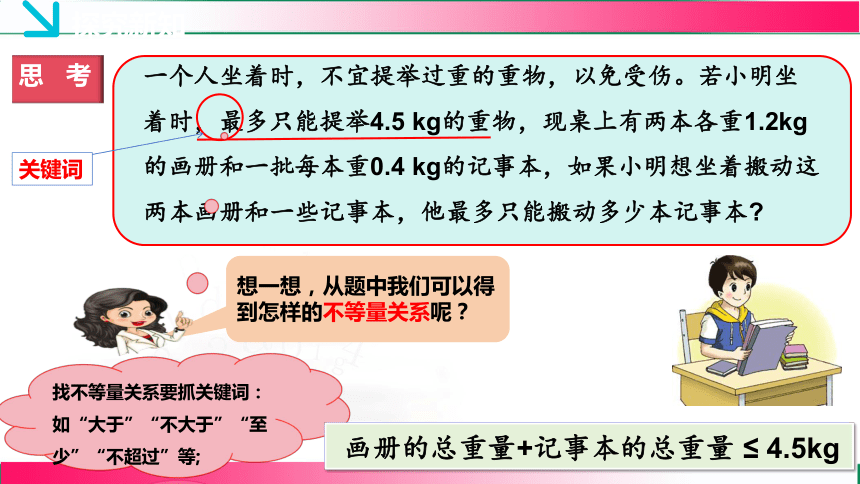
思 考
一个人坐着时,不宜提举过重的重物,以免受伤。若小明坐着时,最多只能提举4.5 kg的重物,现桌上有两本各重1.2kg的画册和一批每本重0.4 kg的记事本,如果小明想坐着搬动这两本画册和一些记事本,他最多只能搬动多少本记事本
想一想,从题中我们可以得到怎样的不等量关系呢?
关键词
找不等量关系要抓关键词:如“大于”“不大于”“至少”“不超过”等;
画册的总重量+记事本的总重量 ≤ 4.5kg
1.2×2
+ ≤4.5
画册的总重+记事本的总重≤4.5kg
解:设小明应搬动x本记事本,则
解这个不等式,得x≤5.25
答:小明最多只应搬动5本记事本.
0.4x
探究新知
思 考
一个人坐着时,不宜提举过重的重物,以免受伤。若小明坐着时,最多只能提举4.5 kg的重物,现桌上有两本各重1.2kg的画册和一批每本重0.4 kg的记事本,如果小明想坐着搬动这两本画册和一些记事本,他最多只能搬动多少本记事本
由于记事本的数目必须是整数,所以x的最大值为5
例题讲解
例1
一种电子琴的进价为每台1800元,如果商店按标价的八折出售,所得利润不低于售价的10%,那么每台电子琴的标价至少是多少元
关键词
想一想,从题中我们可以得到怎样的不等量关系呢?
售价-进价≥售价的10%.
答:每台电子琴的标价至少是2500元。
解 设每台电子琴的标价为x元,那么售出一台电子琴所得的利润不低于(80%x×10%)元。根据题意得
80%x-1800≥80%x×10%
解这个不等式,得x≥2500.
售价-进价≥售价的10%.
审(题)
设(元)
列(不等式)
解(不等式)
检验,作答
例题讲解
例2
为增强自身体魄小华等几名同学只要条件允许,几乎每个星期天都去登山,一般是上午7点出发,到达山顶后休息2 h,下午不超过4点回到出发点。如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶 (图中的7 km,8km,13 km,11 km表示出发点到山顶的路程)
Ⅰ(7km)
Ⅱ(8km)
Ⅲ(13km)
Ⅳ(11km)
图3.4-1
出发点
关键词
想一想,从题中我们可以得到怎样的不等量关系呢?
去时所花时间+休息时间+回来所花时间≤限定的总时间
答:要满足下午不超过4点回到出发点,小华他们最远能登上山顶Ⅳ。
去时所花时间+休息时间+回来所花时间≤限定的总时间
解这个不等式,得x≤12.
解 设从出发点到山顶的距离为x km,则他们去时所花时间为 h,回来所花时间为 h.
又他们在山顶休息了2h,上午7点到下午4点之间相隔9h
例题讲解
用流程图表示运用一元一次不等式解决实际问题的步骤,并与同学交流结果。
实际问题
列不等式
解不等式
结合实际确定答案
找出数量关系
设未知数
探究新知
做一做
总结归纳
列一元一次不等式解应用题的方法步骤
审:认真审题,找出题目中的不等关系,抓住关键词,如“超过”“不大于” “最多”等;
列:列出不等式;
设:设出适当的未知数;
答:检验答案是否符合实际意义,并作答.
解:求出一元一次不等式的解集;
检:检查所求解集是否符合实际情况,并根据实际情况取值;
1. 某学校组织七年级学生到劳动实践教育
基地参加实践活动,某小组的任务是平整土地 ,学校
要求完成全部任务的时间不超过 .开始的半小时,由于操
作不熟练,只平整了 .若设他们在剩余时间内每小时平
整土地 ,则根据题意可列不等式为( )
A
A. B.
C. D.
2. 在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导
火线后,要在炸药爆炸前跑到 以外的安全区域.已知导
火线的燃烧速度是,操作人员跑步的速度是 .为
了保证操作人员的安全,导火线的长度要超过( )
C
A. B. C. D.
3. 沙洲红色旅游景区位于郴州市汝城县西部
文明瑶族乡,感动亿万中国人的“半条被子”故事就发生在这
里,走进“半条被子的温暖”专题陈列馆,这段军民鱼水情深
的故事展现在眼前.某校计划组织学生乘车到该景区进行研学
活动,现有甲、乙两种型号的客车可供租用,已知每辆甲型
客车的租金为280元,每辆乙型客车的租金为220元,若学校
计划租用6辆客车,租车的总租金不超过1 600元,那么最多
租用甲型客车___辆.
4
【点拨】设租用甲型客车辆,则租用乙型客车 辆,
依题意得,解得 .
又因为为整数,所以 的最大值为4.
所以最多租用甲型客车4辆.
故答案为4.
4.[2024·山西] 如图,为加强校园消防安全,
学校计划购买某种型号的水基灭火器和干
粉灭火器共50个.其中水基灭火器的单价为
540元/个,干粉灭火器的单价为380元/个.
若学校购买这两种灭火器的总价不超过21 000元,则最多可
购买这种型号的水基灭火器多少个?
【解】设购买这种型号的水基灭火器 个,
则购买干粉灭火器 个,
根据题意得 ,
解得 .
因为 为整数,
所以 的最大值为12.
答:最多可购买这种型号的水基灭火器12
个.
5. 一艘轮船从某江上游的地匀速驶到下游的地用了 ,
从地匀速返回地用了不到,这段江水流速为 ,轮
船在静水里的往返速度 不变,根据题意可以列出不等式为
( )
C
A. B.
C. D.
6. 如图是2024年5
月份的日历,像图中那样圈住3个数,
如果被圈住的3个数的和不大于66,
则被圈住的三个数中,最大的数
( )
C
A. 不大于21 B. 不大于22 C. 不大于23 D. 不大于20
【点拨】设最小的数为 ,则其他两个
数分别为, .
依题意得 ,
解得 .
所以最大的数不大于 .
故选C.
7. 如图,为了节省空间,李
老师家里的饭碗一般是摞起来
存放的,如果大小和形状都一
样的2只饭碗摞起来的高度为
B
A. 11 B. 12 C. 13 D. 14
,7只饭碗摞起来的高度为 .李老师家的碗柜每格的
高度为 ,则李老师一摞碗最多能放的只数是( )
8. 某市出租车收费标准是:起步价为6元(即行驶距离不超
过应付车费6元),超过后,每增加 加收1.4元
(不足按 收费).某人从甲地到乙地经过的路程是
,出租车费为17.2元,则( )
B
A. B.
C. D.
9.小明家距离学校 .一天中午,小明从家里出发时,离规
定到校时间只剩 ,为了准时到校,他必须加快速度.已
知他每分钟走,若跑步每分钟可跑 .为了不迟到,
小明至少要跑多少分钟?设要跑 ,则列出的不等式为
_________________________.
10. 澧县葡萄酸甜可口,衡山红脆桃甜脆爽口,
都广受顾客喜爱,某水果商店计划购进澧县葡萄和衡山红脆
桃共 ,已知两者的进价和售价如表所示:
进价(元/ ) 售价(元/ )
澧县葡萄 12 20
衡山红脆桃 6 10
若想要此次澧县葡萄和衡山红脆桃全部售完的利润不低于
1 000元,则最多可购进衡山红脆桃_____ .
150
11. 推进中国式现代化,必须坚持不懈夯实
农业基础,推进乡村全面振兴.某合作社着力发展乡村水果网
络销售,在水果收获的季节,该合作社用17 500元从农户处
购进,两种水果共进行销售,其中 种水果的收
购单价为10元/,种水果的收购单价为15元/ .
(1)求, 两种水果各购进多少千克;
【解】设种水果购进,种水果购进 ,
根据题意得解得
所以种水果购进,种水果购进 .
(2)已知种水果运输和仓储过程中质量损失 ,若合作
社计划种水果至少要获得的利润,不计其他费用,求
种水果的最低销售单价.
设种水果的销售单价为元/ ,
根据题意得 ,
解得 .
所以 的最小值为12.5.
所以种水果的最低销售单价为12.5元/ .
课堂小结
实际问题
建立数学模型
(一元一次不等式)
审题、设未知数
根据不等关系列出不等式
数学问题的解
实际问题的解
检验
解一元一次不等式
去括号
移项
合并
系数化为1
应用一元一次不等式解决实际问题的步骤有哪些?
谢谢观看!
3.4 一元一次不等式的应用
第3章 一元一次不等式(组)
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.掌握解一元一次不等式的步骤,会用一元一次不等式解简单的实际问题; (重点)
2.寻找实际问题中的不等关系,建立数学模型
(难点)
学生能够理解一元一次不等式(组)的概念,明确其与一元一次方程的区别与联系。
熟练掌握一元一次不等式(组)的解法,能准确求出其解集,并在数轴上正确表示出来。
过程与方法目标
通过类比一元一次方程的解法探究一元一次不等式(组)的解法,培养学生的类比推理能力和知识迁移能力。
在解决实际问题的过程中,学会将实际问题转化为数学模型,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
通过小组合作学习,培养学生的团队协作精神和交流表达能力。
让学生在探索知识的过程中,体验成功的喜悦,增强学习数学的自信心。
二、教学重难点
教学重点
一元一次不等式(组)的概念和解法。
用数轴表示不等式(组)的解集。
教学难点
不等式基本性质 3 的理解和应用,在不等式两边同时乘以(或除以)同一个负数时,不等号方向要改变。
确定不等式组的解集,尤其是在解复杂的不等式组时,如何准确找到各个不等式解集的公共部分。
三、教学方法
讲授法:通过清晰的讲解,向学生传授一元一次不等式(组)的基本概念、解法步骤和相关理论知识,使学生对新知识有初步的系统认识。
讨论法:组织学生进行小组讨论,针对一元一次不等式(组)与一元一次方程的异同点、不等式组解集的确定方法等问题展开讨论,激发学生的思维,促进学生之间的思想交流与碰撞,培养学生的合作能力和自主探究能力。
练习法:安排适量的练习题,让学生在练习过程中巩固所学的一元一次不等式(组)的解法,及时发现并解决学生在解题过程中出现的问题,提高学生的解题能力和应用知识的能力。
直观演示法:借助数轴,直观地展示不等式(组)的解集,帮助学生更好地理解和掌握解集的概念,突破教学难点。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探究新知
思 考
一个人坐着时,不宜提举过重的重物,以免受伤。若小明坐着时,最多只能提举4.5 kg的重物,现桌上有两本各重1.2kg的画册和一批每本重0.4 kg的记事本,如果小明想坐着搬动这两本画册和一些记事本,他最多只能搬动多少本记事本
想一想,从题中我们可以得到怎样的不等量关系呢?
关键词
找不等量关系要抓关键词:如“大于”“不大于”“至少”“不超过”等;
画册的总重量+记事本的总重量 ≤ 4.5kg
1.2×2
+ ≤4.5
画册的总重+记事本的总重≤4.5kg
解:设小明应搬动x本记事本,则
解这个不等式,得x≤5.25
答:小明最多只应搬动5本记事本.
0.4x
探究新知
思 考
一个人坐着时,不宜提举过重的重物,以免受伤。若小明坐着时,最多只能提举4.5 kg的重物,现桌上有两本各重1.2kg的画册和一批每本重0.4 kg的记事本,如果小明想坐着搬动这两本画册和一些记事本,他最多只能搬动多少本记事本
由于记事本的数目必须是整数,所以x的最大值为5
例题讲解
例1
一种电子琴的进价为每台1800元,如果商店按标价的八折出售,所得利润不低于售价的10%,那么每台电子琴的标价至少是多少元
关键词
想一想,从题中我们可以得到怎样的不等量关系呢?
售价-进价≥售价的10%.
答:每台电子琴的标价至少是2500元。
解 设每台电子琴的标价为x元,那么售出一台电子琴所得的利润不低于(80%x×10%)元。根据题意得
80%x-1800≥80%x×10%
解这个不等式,得x≥2500.
售价-进价≥售价的10%.
审(题)
设(元)
列(不等式)
解(不等式)
检验,作答
例题讲解
例2
为增强自身体魄小华等几名同学只要条件允许,几乎每个星期天都去登山,一般是上午7点出发,到达山顶后休息2 h,下午不超过4点回到出发点。如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶 (图中的7 km,8km,13 km,11 km表示出发点到山顶的路程)
Ⅰ(7km)
Ⅱ(8km)
Ⅲ(13km)
Ⅳ(11km)
图3.4-1
出发点
关键词
想一想,从题中我们可以得到怎样的不等量关系呢?
去时所花时间+休息时间+回来所花时间≤限定的总时间
答:要满足下午不超过4点回到出发点,小华他们最远能登上山顶Ⅳ。
去时所花时间+休息时间+回来所花时间≤限定的总时间
解这个不等式,得x≤12.
解 设从出发点到山顶的距离为x km,则他们去时所花时间为 h,回来所花时间为 h.
又他们在山顶休息了2h,上午7点到下午4点之间相隔9h
例题讲解
用流程图表示运用一元一次不等式解决实际问题的步骤,并与同学交流结果。
实际问题
列不等式
解不等式
结合实际确定答案
找出数量关系
设未知数
探究新知
做一做
总结归纳
列一元一次不等式解应用题的方法步骤
审:认真审题,找出题目中的不等关系,抓住关键词,如“超过”“不大于” “最多”等;
列:列出不等式;
设:设出适当的未知数;
答:检验答案是否符合实际意义,并作答.
解:求出一元一次不等式的解集;
检:检查所求解集是否符合实际情况,并根据实际情况取值;
1. 某学校组织七年级学生到劳动实践教育
基地参加实践活动,某小组的任务是平整土地 ,学校
要求完成全部任务的时间不超过 .开始的半小时,由于操
作不熟练,只平整了 .若设他们在剩余时间内每小时平
整土地 ,则根据题意可列不等式为( )
A
A. B.
C. D.
2. 在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导
火线后,要在炸药爆炸前跑到 以外的安全区域.已知导
火线的燃烧速度是,操作人员跑步的速度是 .为
了保证操作人员的安全,导火线的长度要超过( )
C
A. B. C. D.
3. 沙洲红色旅游景区位于郴州市汝城县西部
文明瑶族乡,感动亿万中国人的“半条被子”故事就发生在这
里,走进“半条被子的温暖”专题陈列馆,这段军民鱼水情深
的故事展现在眼前.某校计划组织学生乘车到该景区进行研学
活动,现有甲、乙两种型号的客车可供租用,已知每辆甲型
客车的租金为280元,每辆乙型客车的租金为220元,若学校
计划租用6辆客车,租车的总租金不超过1 600元,那么最多
租用甲型客车___辆.
4
【点拨】设租用甲型客车辆,则租用乙型客车 辆,
依题意得,解得 .
又因为为整数,所以 的最大值为4.
所以最多租用甲型客车4辆.
故答案为4.
4.[2024·山西] 如图,为加强校园消防安全,
学校计划购买某种型号的水基灭火器和干
粉灭火器共50个.其中水基灭火器的单价为
540元/个,干粉灭火器的单价为380元/个.
若学校购买这两种灭火器的总价不超过21 000元,则最多可
购买这种型号的水基灭火器多少个?
【解】设购买这种型号的水基灭火器 个,
则购买干粉灭火器 个,
根据题意得 ,
解得 .
因为 为整数,
所以 的最大值为12.
答:最多可购买这种型号的水基灭火器12
个.
5. 一艘轮船从某江上游的地匀速驶到下游的地用了 ,
从地匀速返回地用了不到,这段江水流速为 ,轮
船在静水里的往返速度 不变,根据题意可以列出不等式为
( )
C
A. B.
C. D.
6. 如图是2024年5
月份的日历,像图中那样圈住3个数,
如果被圈住的3个数的和不大于66,
则被圈住的三个数中,最大的数
( )
C
A. 不大于21 B. 不大于22 C. 不大于23 D. 不大于20
【点拨】设最小的数为 ,则其他两个
数分别为, .
依题意得 ,
解得 .
所以最大的数不大于 .
故选C.
7. 如图,为了节省空间,李
老师家里的饭碗一般是摞起来
存放的,如果大小和形状都一
样的2只饭碗摞起来的高度为
B
A. 11 B. 12 C. 13 D. 14
,7只饭碗摞起来的高度为 .李老师家的碗柜每格的
高度为 ,则李老师一摞碗最多能放的只数是( )
8. 某市出租车收费标准是:起步价为6元(即行驶距离不超
过应付车费6元),超过后,每增加 加收1.4元
(不足按 收费).某人从甲地到乙地经过的路程是
,出租车费为17.2元,则( )
B
A. B.
C. D.
9.小明家距离学校 .一天中午,小明从家里出发时,离规
定到校时间只剩 ,为了准时到校,他必须加快速度.已
知他每分钟走,若跑步每分钟可跑 .为了不迟到,
小明至少要跑多少分钟?设要跑 ,则列出的不等式为
_________________________.
10. 澧县葡萄酸甜可口,衡山红脆桃甜脆爽口,
都广受顾客喜爱,某水果商店计划购进澧县葡萄和衡山红脆
桃共 ,已知两者的进价和售价如表所示:
进价(元/ ) 售价(元/ )
澧县葡萄 12 20
衡山红脆桃 6 10
若想要此次澧县葡萄和衡山红脆桃全部售完的利润不低于
1 000元,则最多可购进衡山红脆桃_____ .
150
11. 推进中国式现代化,必须坚持不懈夯实
农业基础,推进乡村全面振兴.某合作社着力发展乡村水果网
络销售,在水果收获的季节,该合作社用17 500元从农户处
购进,两种水果共进行销售,其中 种水果的收
购单价为10元/,种水果的收购单价为15元/ .
(1)求, 两种水果各购进多少千克;
【解】设种水果购进,种水果购进 ,
根据题意得解得
所以种水果购进,种水果购进 .
(2)已知种水果运输和仓储过程中质量损失 ,若合作
社计划种水果至少要获得的利润,不计其他费用,求
种水果的最低销售单价.
设种水果的销售单价为元/ ,
根据题意得 ,
解得 .
所以 的最小值为12.5.
所以种水果的最低销售单价为12.5元/ .
课堂小结
实际问题
建立数学模型
(一元一次不等式)
审题、设未知数
根据不等关系列出不等式
数学问题的解
实际问题的解
检验
解一元一次不等式
去括号
移项
合并
系数化为1
应用一元一次不等式解决实际问题的步骤有哪些?
谢谢观看!
同课章节目录
