4.1.1平面内两条直线的位置关系 课件(共23张PPT)
文档属性
| 名称 | 4.1.1平面内两条直线的位置关系 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 07:41:48 | ||
图片预览







文档简介
(共23张PPT)
4.1 .1平面内两条直线
的位置关系
第4章 平面内的两条直线
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解平行线的概念,知道同一平面内两直线的位置关系.
2.掌握平行基本事实,了解平行线具有传递性.
3.会用三角尺和直尺过已知直线外一点画这条直线的平行线.(难点)
学生能够理解一元一次不等式(组)的概念,明确其与一元一次方程的区别与联系。
熟练掌握一元一次不等式(组)的解法,能准确求出其解集,并在数轴上正确表示出来。
过程与方法目标
通过类比一元一次方程的解法探究一元一次不等式(组)的解法,培养学生的类比推理能力和知识迁移能力。
在解决实际问题的过程中,学会将实际问题转化为数学模型,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
通过小组合作学习,培养学生的团队协作精神和交流表达能力。
让学生在探索知识的过程中,体验成功的喜悦,增强学习数学的自信心。
二、教学重难点
教学重点
一元一次不等式(组)的概念和解法。
用数轴表示不等式(组)的解集。
教学难点
不等式基本性质 3 的理解和应用,在不等式两边同时乘以(或除以)同一个负数时,不等号方向要改变。
确定不等式组的解集,尤其是在解复杂的不等式组时,如何准确找到各个不等式解集的公共部分。
三、教学方法
讲授法:通过清晰的讲解,向学生传授一元一次不等式(组)的基本概念、解法步骤和相关理论知识,使学生对新知识有初步的系统认识。
讨论法:组织学生进行小组讨论,针对一元一次不等式(组)与一元一次方程的异同点、不等式组解集的确定方法等问题展开讨论,激发学生的思维,促进学生之间的思想交流与碰撞,培养学生的合作能力和自主探究能力。
练习法:安排适量的练习题,让学生在练习过程中巩固所学的一元一次不等式(组)的解法,及时发现并解决学生在解题过程中出现的问题,提高学生的解题能力和应用知识的能力。
直观演示法:借助数轴,直观地展示不等式(组)的解集,帮助学生更好地理解和掌握解集的概念,突破教学难点。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
新课导入
探究新知
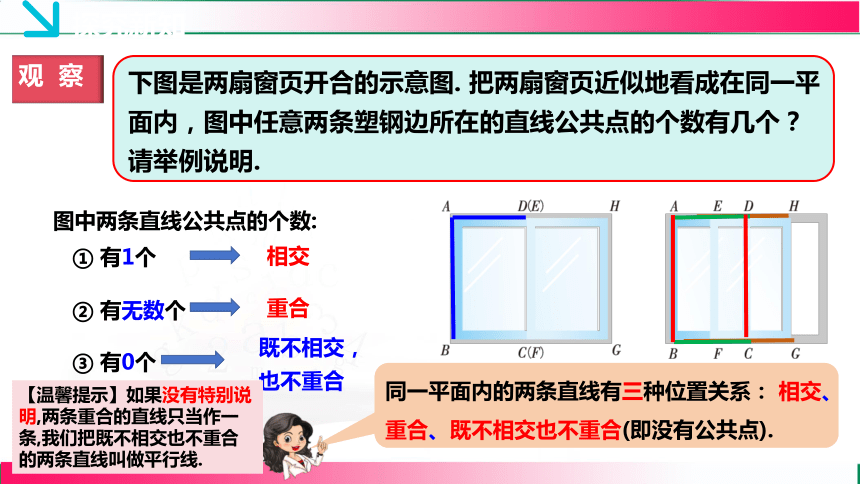
观 察
下图是两扇窗页开合的示意图. 把两扇窗页近似地看成在同一平面内,图中任意两条塑钢边所在的直线公共点的个数有几个?请举例说明.
同一平面内的两条直线有三种位置关系: 相交、重合、既不相交也不重合(即没有公共点).
图中两条直线公共点的个数:
① 有1个
② 有无数个
③ 有0个
相交
重合
既不相交,
也不重合
【温馨提示】如果没有特别说明,两条重合的直线只当作一条,我们把既不相交也不重合的两条直线叫做平行线.
总结归纳
平行线:
在同一平面内,没有公共点的两条直线叫作平行线.
探究新知
1.如图,直线 AB 与 CD 是平行线.记做“ ”,这里“ ”是平行符号. 读做“ ”.
2.若用 a、b 表示这两条直线,那么直线 a 与直线 b 平行,记做“ ”,读做“ ”.
AB∥ CD
∥
AB 平行于 CD
a∥ b
a 平行于 b
平行符号:∥
探究新知
议一议
观察教室黑板的上、下边缘所在的直线,它们可以看作平行线吗?你还能从教室里找到哪些平行线的实例?将结果与同学们交流.
平行
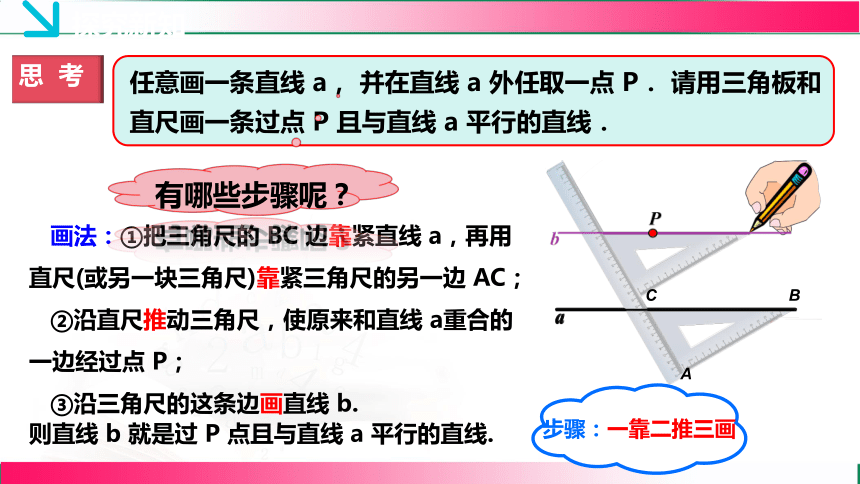
画法:①把三角尺的 BC 边靠紧直线 a,再用直尺(或另一块三角尺)靠紧三角尺的另一边 AC;
②沿直尺推动三角尺,使原来和直线 a重合的一边经过点 P;
③沿三角尺的这条边画直线 b.
则直线 b 就是过 P 点且与直线 a 平行的直线.
B
A
C
探究新知
思 考
任意画一条直线 a, 并在直线 a 外任取一点 P. 请用三角板和直尺画一条过点 P 且与直线 a 平行的直线.
有哪些步骤呢?
步骤:一靠二推三画
总结归纳
注意:1、过直线外一点,而不是直线上一点。
2、有且只有,是确定
平行的基本事实:
过直线外一点有且只有一条直线与这条直线平行.
探究新知
探究新知
说一说
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
若 a 与 c 不平行, 就会相交于某一点 P ,那么过点P 就有两条直线与 b 平行, 这是不可能的. 所以 a∥c.
平行于同一直线的两条直线平行.
你能得到什么结论?
几何语言:
因为 a∥b,c∥b,
所以 a∥c (平行于同一条直线的两条直线互相平行).
1. 在同一平面内,不重合的两条直线的位置关系是( )
C
A. 平行 B. 相交
C. 平行或相交 D. 平行或垂直
(第2题)
2. 教材P92说一说 如图, ,
过点画,则与 的位置关
系是_________,理由是______________
___________________.
平行于同一条直线的两条直线平行
3.如图,,,则点,, 在同一条直线
上,理由是__________________________________________
___.
过直线外一点有且只有一条直线与这条直线平行
(第3题)
4.分别写出下列语句表示的图形(填序号):
(1)过点的三条直线与另一条直线分别相交于,, 三点:
____.
③
(2)以直线上一点为顶点,在直线的同侧作 和
____.
②
(3)过点的一条直线和以 为端点的两条射线与另一条直
线分别相交于,, 三点:____.
①
5. 如图,在内有一点 .
(1)过点画 .
【解】如图所示.
(2)过点画 .
如图所示.
(3)用量角器量一量与的夹角与
的大小有怎样的关系?
如图,与 的夹角有两个,分别是
,, ,
所以和的夹角与 相等或互补.
与 是互补关系,容易漏掉.
6. 下列推理正确的是( )
C
A. 因为,,所以
B. 因为,,所以
C. 因为,,所以
D. 因为,,所以
7. 在同一平面内,如果直线与平行,直线与 垂直,则这
三条直线中所有交点的个数为( )
B
A. 1 B. 2 C. 3 D. 1或3
8. 已知直线和一点,过点画直线 的平行线,可画
( )
C
A. 1条 B. 0条 C. 1条或0条 D. 无数条
【点拨】如果点在直线上,过点画直线 的平行线可画
0条;如果点在直线外,过点画直线 的平行线可画1条.
9.在同一平面内,直线与 满足下列条件:
(1)与没有公共点,则与 ______;
(2)与有且只有一个公共点,则与 ______;
(3)与有两个公共点,则与 ______.
平行
相交
重合
课堂小结
平行基本事实
过直线外一点有且只有一条直线与这条直线平行.
平行的传递性
平行于同一条直线的两条直线平行.
在同一平面内,没有公共点的两条直线叫作行平线.
平行线概念
AB∥ CD
a∥ b
平面内两条直
线的位置关系
谢谢观看!
4.1 .1平面内两条直线
的位置关系
第4章 平面内的两条直线
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1.理解平行线的概念,知道同一平面内两直线的位置关系.
2.掌握平行基本事实,了解平行线具有传递性.
3.会用三角尺和直尺过已知直线外一点画这条直线的平行线.(难点)
学生能够理解一元一次不等式(组)的概念,明确其与一元一次方程的区别与联系。
熟练掌握一元一次不等式(组)的解法,能准确求出其解集,并在数轴上正确表示出来。
过程与方法目标
通过类比一元一次方程的解法探究一元一次不等式(组)的解法,培养学生的类比推理能力和知识迁移能力。
在解决实际问题的过程中,学会将实际问题转化为数学模型,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
通过小组合作学习,培养学生的团队协作精神和交流表达能力。
让学生在探索知识的过程中,体验成功的喜悦,增强学习数学的自信心。
二、教学重难点
教学重点
一元一次不等式(组)的概念和解法。
用数轴表示不等式(组)的解集。
教学难点
不等式基本性质 3 的理解和应用,在不等式两边同时乘以(或除以)同一个负数时,不等号方向要改变。
确定不等式组的解集,尤其是在解复杂的不等式组时,如何准确找到各个不等式解集的公共部分。
三、教学方法
讲授法:通过清晰的讲解,向学生传授一元一次不等式(组)的基本概念、解法步骤和相关理论知识,使学生对新知识有初步的系统认识。
讨论法:组织学生进行小组讨论,针对一元一次不等式(组)与一元一次方程的异同点、不等式组解集的确定方法等问题展开讨论,激发学生的思维,促进学生之间的思想交流与碰撞,培养学生的合作能力和自主探究能力。
练习法:安排适量的练习题,让学生在练习过程中巩固所学的一元一次不等式(组)的解法,及时发现并解决学生在解题过程中出现的问题,提高学生的解题能力和应用知识的能力。
直观演示法:借助数轴,直观地展示不等式(组)的解集,帮助学生更好地理解和掌握解集的概念,突破教学难点。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
新课导入
探究新知
观 察
下图是两扇窗页开合的示意图. 把两扇窗页近似地看成在同一平面内,图中任意两条塑钢边所在的直线公共点的个数有几个?请举例说明.
同一平面内的两条直线有三种位置关系: 相交、重合、既不相交也不重合(即没有公共点).
图中两条直线公共点的个数:
① 有1个
② 有无数个
③ 有0个
相交
重合
既不相交,
也不重合
【温馨提示】如果没有特别说明,两条重合的直线只当作一条,我们把既不相交也不重合的两条直线叫做平行线.
总结归纳
平行线:
在同一平面内,没有公共点的两条直线叫作平行线.
探究新知
1.如图,直线 AB 与 CD 是平行线.记做“ ”,这里“ ”是平行符号. 读做“ ”.
2.若用 a、b 表示这两条直线,那么直线 a 与直线 b 平行,记做“ ”,读做“ ”.
AB∥ CD
∥
AB 平行于 CD
a∥ b
a 平行于 b
平行符号:∥
探究新知
议一议
观察教室黑板的上、下边缘所在的直线,它们可以看作平行线吗?你还能从教室里找到哪些平行线的实例?将结果与同学们交流.
平行
画法:①把三角尺的 BC 边靠紧直线 a,再用直尺(或另一块三角尺)靠紧三角尺的另一边 AC;
②沿直尺推动三角尺,使原来和直线 a重合的一边经过点 P;
③沿三角尺的这条边画直线 b.
则直线 b 就是过 P 点且与直线 a 平行的直线.
B
A
C
探究新知
思 考
任意画一条直线 a, 并在直线 a 外任取一点 P. 请用三角板和直尺画一条过点 P 且与直线 a 平行的直线.
有哪些步骤呢?
步骤:一靠二推三画
总结归纳
注意:1、过直线外一点,而不是直线上一点。
2、有且只有,是确定
平行的基本事实:
过直线外一点有且只有一条直线与这条直线平行.
探究新知
探究新知
说一说
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
若 a 与 c 不平行, 就会相交于某一点 P ,那么过点P 就有两条直线与 b 平行, 这是不可能的. 所以 a∥c.
平行于同一直线的两条直线平行.
你能得到什么结论?
几何语言:
因为 a∥b,c∥b,
所以 a∥c (平行于同一条直线的两条直线互相平行).
1. 在同一平面内,不重合的两条直线的位置关系是( )
C
A. 平行 B. 相交
C. 平行或相交 D. 平行或垂直
(第2题)
2. 教材P92说一说 如图, ,
过点画,则与 的位置关
系是_________,理由是______________
___________________.
平行于同一条直线的两条直线平行
3.如图,,,则点,, 在同一条直线
上,理由是__________________________________________
___.
过直线外一点有且只有一条直线与这条直线平行
(第3题)
4.分别写出下列语句表示的图形(填序号):
(1)过点的三条直线与另一条直线分别相交于,, 三点:
____.
③
(2)以直线上一点为顶点,在直线的同侧作 和
____.
②
(3)过点的一条直线和以 为端点的两条射线与另一条直
线分别相交于,, 三点:____.
①
5. 如图,在内有一点 .
(1)过点画 .
【解】如图所示.
(2)过点画 .
如图所示.
(3)用量角器量一量与的夹角与
的大小有怎样的关系?
如图,与 的夹角有两个,分别是
,, ,
所以和的夹角与 相等或互补.
与 是互补关系,容易漏掉.
6. 下列推理正确的是( )
C
A. 因为,,所以
B. 因为,,所以
C. 因为,,所以
D. 因为,,所以
7. 在同一平面内,如果直线与平行,直线与 垂直,则这
三条直线中所有交点的个数为( )
B
A. 1 B. 2 C. 3 D. 1或3
8. 已知直线和一点,过点画直线 的平行线,可画
( )
C
A. 1条 B. 0条 C. 1条或0条 D. 无数条
【点拨】如果点在直线上,过点画直线 的平行线可画
0条;如果点在直线外,过点画直线 的平行线可画1条.
9.在同一平面内,直线与 满足下列条件:
(1)与没有公共点,则与 ______;
(2)与有且只有一个公共点,则与 ______;
(3)与有两个公共点,则与 ______.
平行
相交
重合
课堂小结
平行基本事实
过直线外一点有且只有一条直线与这条直线平行.
平行的传递性
平行于同一条直线的两条直线平行.
在同一平面内,没有公共点的两条直线叫作行平线.
平行线概念
AB∥ CD
a∥ b
平面内两条直
线的位置关系
谢谢观看!
同课章节目录
