5.3 图形变换的简单应用 课件(共26张PPT)
文档属性
| 名称 | 5.3 图形变换的简单应用 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 18:42:41 | ||
图片预览





文档简介
(共26张PPT)
5.3 图形变换的简单应用
5.1.1 轴对称图形
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
图案欣赏
情境引入
在平面内,将一个图形沿某个方向移动一定的距离,
这样的图形运动称为平移。
平移的概念:
平移的性质:
1、平移不改变图形的大小和形状。
2、对应点所连的线平行且相等。
3、对应线段平行且相等。
4、对应角相等。
知识回顾
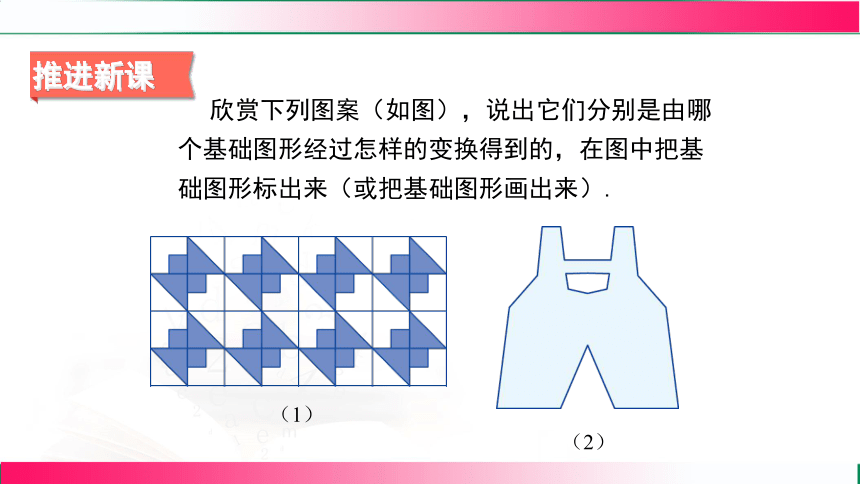
欣赏下列图案(如图),说出它们分别是由哪个基础图形经过怎样的变换得到的,在图中把基础图形标出来(或把基础图形画出来).
推进新课
(1)
(2)
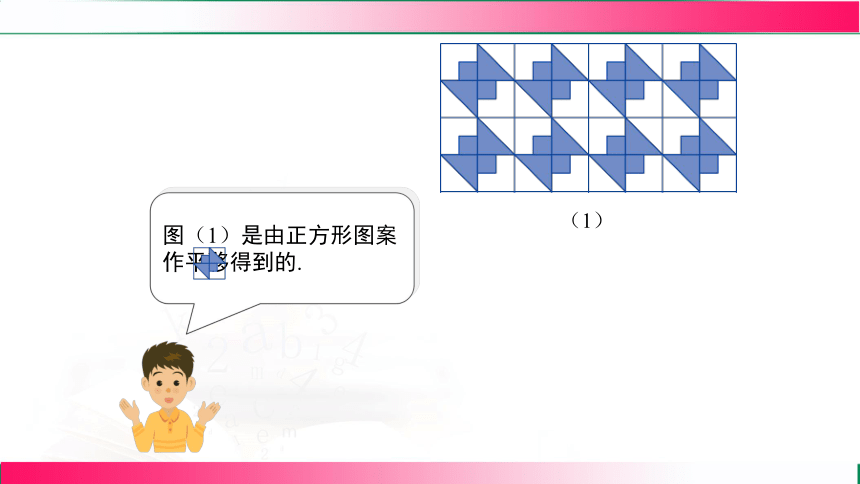
图(1)是由正方形图案 作平移得到的.
(1)
图(2)是由图 作轴对称变换得到的.
(2)
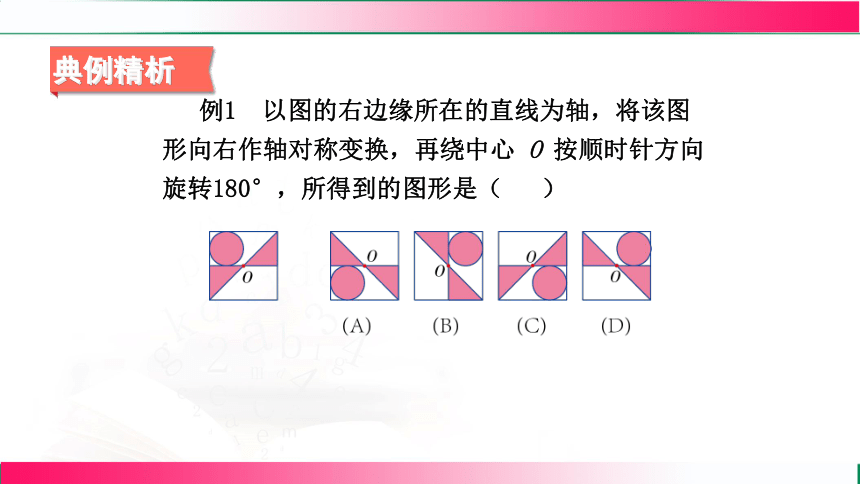
例1 以图的右边缘所在的直线为轴,将该图形向右作轴对称变换,再绕中心 O 按顺时针方向旋转180°,所得到的图形是( )
典例精析
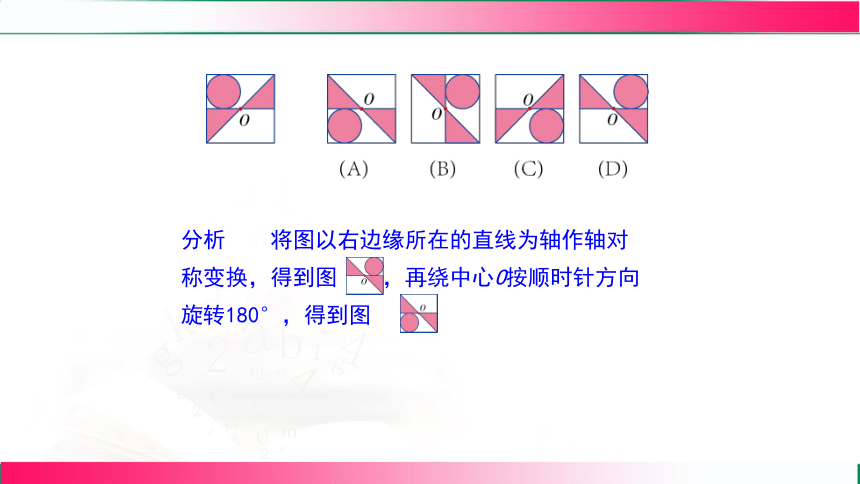
分析 将图以右边缘所在的直线为轴作轴对称变换,得到图 ,再绕中心O按顺时针方向旋转180°,得到图 .
下图是一种正方形的瓷砖.
(1)请用4块所给瓷砖拼一个正方形图案(至少
设计3种不同的图案);
(2)如果给你16块这样的正方形瓷砖,要求设计
的图案为轴对称图形,你可以设计出来吗?
例2
下图中只能用其中一部分平移可以得到的是( ).
轴对称、平移不改变图形的形状和大小.平移前后图形对应点连线平行且相等,故选B.
解
B
D
A
B
C
例3
圆弧与扇形的对称轴是过弧中点和圆心的直线.角的对称轴是角平分线所在的直线.菱形和等腰梯形是轴对称图形.
解
如图,下列几何图形中,一定是轴对称图形的有( ).
A.2个 B.3个 C.4个 D.5个
D
1、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,以三个正三角形的公
共顶点为旋转中心,分别按顺时针、逆时针方向旋转600,即可
得到该图案。
1. [2024·廊坊广阳区二模] 如图所示,甲图案变为乙图案,
可以用( )
A
(第1题)
A. 旋转、平移 B. 平移、轴对称
C. 旋转、轴对称 D. 平移
2.在边长为1的正方形网格中,右边的“小鱼”图案是由左边的
图案经过一次平移得到的,则平移的距离是___.
6
(第2题)
3.在如图所示的网格中,每个小正方形的边长为1.
(1)以所在的直线为对称轴,画出四边形 的轴对
称图形 ;
【解】如图所示.
(2)将以点为旋转中心,顺时针旋转 后,再向
下平移8个单位,然后向左平移6个单位,得到 ,请
将(1)、(2)中得到的图形用铅笔涂黑,你将得到一幅美
丽的图案.
如图所示.
4. 如图,小明在的网格纸上将正方形 从当前位置
开始进行一次平移操作,平移后的正方形顶点在格点上,则
使平移前后的两个正方形组成轴对称图形平移方向有( )
C
A. 3个 B. 4个 C. 5个 D. 无数个
5.如图,小默同学在边长为1的小正方形组
成的网格中,以 为基本图形,利用
图形的旋转变换绘制风车风轮的平面图形.
请根据下列要求解答问题.
(1)绕点逆时针旋转____度得到 ;
90
(2)在图中画出将绕点顺时针旋转 后得到的
;
【解】如图所示, 即
为所求.
(3)完整的风车风轮平面图形的面积为____.
20
6.为创建绿色校园,学校决定对一块
正方形的空地进行种植花草,现向学
生征集设计图案.图案要求只能用圆
弧在正方形内加以设计,使正方形和
所画的圆弧构成图案,种植花草部分
用阴影表示.请你运用平移、旋转、轴对称等知识,在图③、
图④、图⑤中画出三种不同的设计图案(温馨提示:在两个
图案中,只有半径变化而圆心不变的图案属于同一种,例如:
图①、图②只能算一种).
【解】答案不唯一,如图
所示.
图形间的变换关系
1 旋转——旋转中心、方向、角度和次数
2 平移——平移的方向、距离和次数
3 轴对称——对称轴
4 旋转与平移的组合
5 旋转与轴对称的组合
6 轴对称与平移的组合
找准基本图形
学生能够准确理解旋转的定义,清晰识别生活中的旋转现象。
深入掌握旋转的性质,包括旋转前后图形的对应点、对应线段、对应角之间的关系。
熟练运用旋转的知识,根据给定的旋转中心、旋转方向和旋转角度,画出简单平面图形旋转后的图形。
学会利用旋转知识解决实际问题,如计算旋转后图形的位置、角度等。
过程与方法目标
通过观察、操作、实验、分析等活动,有效培养学生的空间观念、动手操作能力、逻辑思维能力以及数学抽象能力。
经历从具体实例中抽象出旋转概念和性质的过程,深刻体会从特殊到一般、从直观到抽象的数学思想方法。
情感态度与价值观目标
充分感受生活中旋转现象的广泛存在,深刻体会数学与生活的紧密联系,极大激发学生学习数学的兴趣。
通过小组合作探究,切实培养学生的合作意识和团队精神,让学生在探索活动中获得成功的体验,显著增强学习数学的自信心。
二、教学重难点
重点
透彻理解旋转的定义和性质。
能够精准画出简单平面图形旋转后的图形
谢谢观看!
5.3 图形变换的简单应用
5.1.1 轴对称图形
2024湘教版数学七年级下册
授课教师:********
班 级:********
时 间:********
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
图案欣赏
情境引入
在平面内,将一个图形沿某个方向移动一定的距离,
这样的图形运动称为平移。
平移的概念:
平移的性质:
1、平移不改变图形的大小和形状。
2、对应点所连的线平行且相等。
3、对应线段平行且相等。
4、对应角相等。
知识回顾
欣赏下列图案(如图),说出它们分别是由哪个基础图形经过怎样的变换得到的,在图中把基础图形标出来(或把基础图形画出来).
推进新课
(1)
(2)
图(1)是由正方形图案 作平移得到的.
(1)
图(2)是由图 作轴对称变换得到的.
(2)
例1 以图的右边缘所在的直线为轴,将该图形向右作轴对称变换,再绕中心 O 按顺时针方向旋转180°,所得到的图形是( )
典例精析
分析 将图以右边缘所在的直线为轴作轴对称变换,得到图 ,再绕中心O按顺时针方向旋转180°,得到图 .
下图是一种正方形的瓷砖.
(1)请用4块所给瓷砖拼一个正方形图案(至少
设计3种不同的图案);
(2)如果给你16块这样的正方形瓷砖,要求设计
的图案为轴对称图形,你可以设计出来吗?
例2
下图中只能用其中一部分平移可以得到的是( ).
轴对称、平移不改变图形的形状和大小.平移前后图形对应点连线平行且相等,故选B.
解
B
D
A
B
C
例3
圆弧与扇形的对称轴是过弧中点和圆心的直线.角的对称轴是角平分线所在的直线.菱形和等腰梯形是轴对称图形.
解
如图,下列几何图形中,一定是轴对称图形的有( ).
A.2个 B.3个 C.4个 D.5个
D
1、下图是由三个正三角形拼成的,它可以看作由其中一个三角形经过怎样的变化而得到的?
把中间的正三角形看做“基本图案”,以三个正三角形的公
共顶点为旋转中心,分别按顺时针、逆时针方向旋转600,即可
得到该图案。
1. [2024·廊坊广阳区二模] 如图所示,甲图案变为乙图案,
可以用( )
A
(第1题)
A. 旋转、平移 B. 平移、轴对称
C. 旋转、轴对称 D. 平移
2.在边长为1的正方形网格中,右边的“小鱼”图案是由左边的
图案经过一次平移得到的,则平移的距离是___.
6
(第2题)
3.在如图所示的网格中,每个小正方形的边长为1.
(1)以所在的直线为对称轴,画出四边形 的轴对
称图形 ;
【解】如图所示.
(2)将以点为旋转中心,顺时针旋转 后,再向
下平移8个单位,然后向左平移6个单位,得到 ,请
将(1)、(2)中得到的图形用铅笔涂黑,你将得到一幅美
丽的图案.
如图所示.
4. 如图,小明在的网格纸上将正方形 从当前位置
开始进行一次平移操作,平移后的正方形顶点在格点上,则
使平移前后的两个正方形组成轴对称图形平移方向有( )
C
A. 3个 B. 4个 C. 5个 D. 无数个
5.如图,小默同学在边长为1的小正方形组
成的网格中,以 为基本图形,利用
图形的旋转变换绘制风车风轮的平面图形.
请根据下列要求解答问题.
(1)绕点逆时针旋转____度得到 ;
90
(2)在图中画出将绕点顺时针旋转 后得到的
;
【解】如图所示, 即
为所求.
(3)完整的风车风轮平面图形的面积为____.
20
6.为创建绿色校园,学校决定对一块
正方形的空地进行种植花草,现向学
生征集设计图案.图案要求只能用圆
弧在正方形内加以设计,使正方形和
所画的圆弧构成图案,种植花草部分
用阴影表示.请你运用平移、旋转、轴对称等知识,在图③、
图④、图⑤中画出三种不同的设计图案(温馨提示:在两个
图案中,只有半径变化而圆心不变的图案属于同一种,例如:
图①、图②只能算一种).
【解】答案不唯一,如图
所示.
图形间的变换关系
1 旋转——旋转中心、方向、角度和次数
2 平移——平移的方向、距离和次数
3 轴对称——对称轴
4 旋转与平移的组合
5 旋转与轴对称的组合
6 轴对称与平移的组合
找准基本图形
学生能够准确理解旋转的定义,清晰识别生活中的旋转现象。
深入掌握旋转的性质,包括旋转前后图形的对应点、对应线段、对应角之间的关系。
熟练运用旋转的知识,根据给定的旋转中心、旋转方向和旋转角度,画出简单平面图形旋转后的图形。
学会利用旋转知识解决实际问题,如计算旋转后图形的位置、角度等。
过程与方法目标
通过观察、操作、实验、分析等活动,有效培养学生的空间观念、动手操作能力、逻辑思维能力以及数学抽象能力。
经历从具体实例中抽象出旋转概念和性质的过程,深刻体会从特殊到一般、从直观到抽象的数学思想方法。
情感态度与价值观目标
充分感受生活中旋转现象的广泛存在,深刻体会数学与生活的紧密联系,极大激发学生学习数学的兴趣。
通过小组合作探究,切实培养学生的合作意识和团队精神,让学生在探索活动中获得成功的体验,显著增强学习数学的自信心。
二、教学重难点
重点
透彻理解旋转的定义和性质。
能够精准画出简单平面图形旋转后的图形
谢谢观看!
同课章节目录
