第20章章末复习 课件(共32张PPT)
文档属性
| 名称 | 第20章章末复习 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 08:00:59 | ||
图片预览









文档简介
(共32张PPT)
章末复习
第二十章 数据的分析
人教版(2024)数学八年级下册
授课教师:********
班 级:********
时 间:********
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
算术平均数
概念
拓展
=(x1+x2+ +xn).
① nx1,nx2,…,nxn的平均数为n;
② x1+b,x2+b,…,xn+b的平均数为+b;
③ nx1+b,nx2+b,…,nxn+b的平均数为n+b.
知识梳理
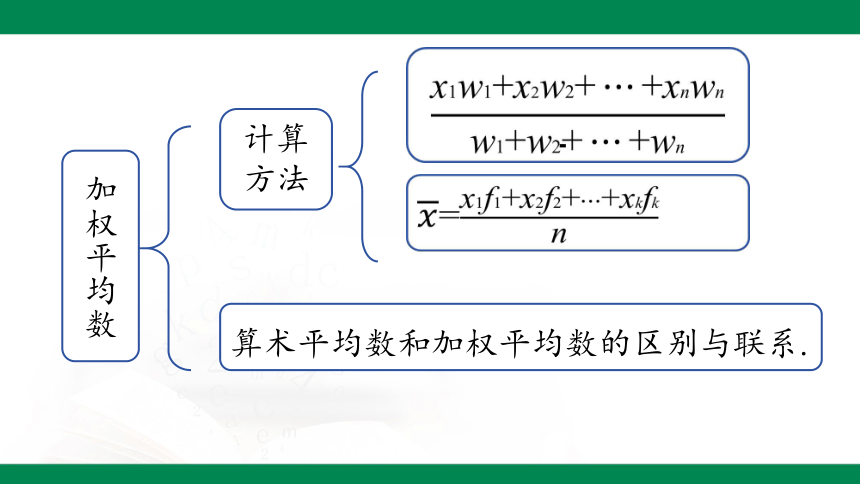
加权平均数
计算
方法
算术平均数和加权平均数的区别与联系.
=
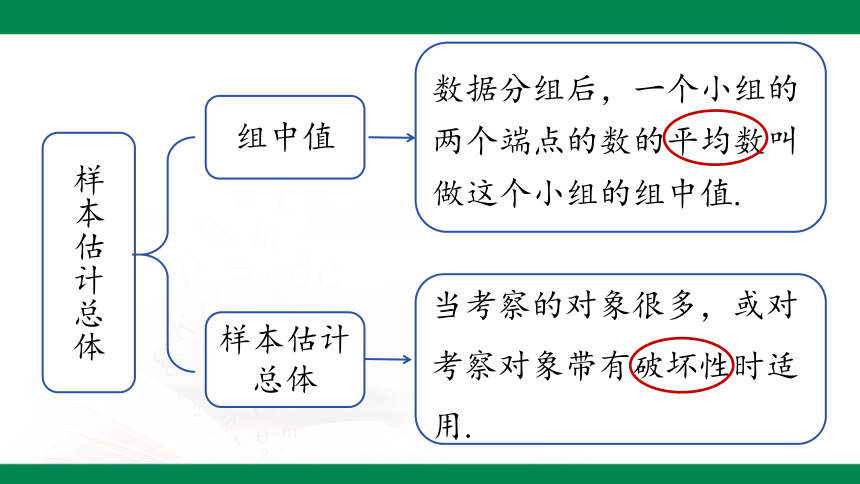
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当考察的对象很多,或对考察对象带有破坏性时适用.
中位数
概念
注意
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
①按照大小顺序排列;
②可能是这组数据中的某个数,也可能不是这组数据中的数.
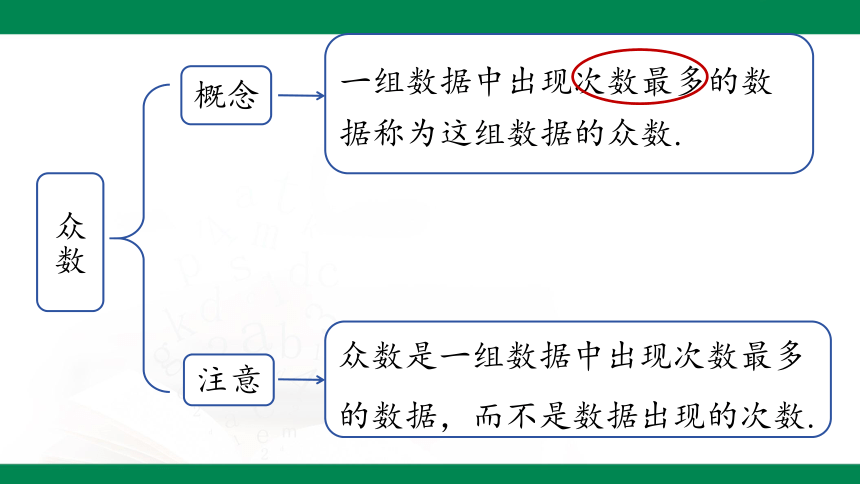
众数
概念
注意
一组数据中出现次数最多的数据称为这组数据的众数.
众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
1. 算术平均数
一般地,如果有 n 个数 x1,x2, ,xn,那么我们把(x1+x2+ +xn)叫做这 n 个数的算术平均数,简称平均数,记作 ,读作 x拔,则有 =(x1+x2+ +xn).
2. 加权平均数
一般地,如果有 n 个数 x1,x2, ,xn 的权分别为 w1,w2, ,wn,那么我们把叫做这n个数的加权平均数.
在求 n 个数的平均数时,如果 x1 出现 f1 次, x2 出现 f2 次, , xk 出现 fk 次(这里的 f1+ f2+ +fk =n),那么这 n 个数的平均数 = .也叫做 x1,x2, ,xk 这 k 个数的加权平均数,其中 f1, f2, , fk分别叫做 x1,x2, ,xk 的权.
3. 用样本平均数估计总体平均数
(1)组中值:数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
(2)用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
4. 中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
5. 众数
一组数据中出现次数最多的数据称为这组数据的众数.
注意:众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
方差
计算公式
意义
+….
方差越大,数据的波动越大;方差越小,数据的波动越小.
知识梳理
方差
估算
意义
用样本的方差估计总体的方差.
根据方差的大小来判断总体的稳定情况.
1. 方差
设有 n 个数据 x1,x2, ,xn,各数据与它们的平均数 的差的平方分别是,,
我们用这些值的平均数,即用+
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作 .
2. 方差的意义
方差可以反映数据的波动程度,即:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
3. 用样本方差估计总体方差
用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
1.求下列数据的方差.
2,3,5,7,7,6
解:
重点解析
求数据的方差,先求出数据的平均数.
重难点1:方差的计算
一、核心知识巩固
考点1 平均数、中位数、众数
1.[2024 湖南] 某班的5名同学1分钟跳绳的成绩(单位:次)分别为:
179,130,192,158,141.这组数据的中位数是( )
B
A.130 B.158 C.160 D.192
2.[2024 无锡] 一组数据:31,32,35,37,35,这组数据的平均数和
中位数分别是( )
C
A.34,34 B.35,35 C.34,35 D.35,34
3.[2024 扬州] 第8个全国近视防控宣传教育月的主题是“有效减少近视
发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学
视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 4 4 7 11 10 5 3
这45名同学视力检查数据的众数是( )
B
A.4.6 B.4.7 C.4.8 D.4.9
4.[2024 南京鼓楼区一模] 如图为某班35名学
生投篮成绩的条形统计图,其中上面部分数据
破损导致数据不完全.已知此班学生投篮成绩
的中位数是5,则根据下图,无法确定下列哪
一选项中的数值( )
C
A.4球以下的人数 B.5球以下的人数
C.6球以下的人数 D.7球以下的人数
(第5题)
5. 某校拟招聘一名优秀的数学教师,
设置了笔试、面试、试讲三项水平测试,综合成绩
按照笔试占,面试占,试讲占 进行计
算,小徐的三项测试成绩如图所示,则她的综合成
绩为_____分.
85.8
(第6题)
6.[2024 镇江] 小丽6次射击的成绩如图所示,则她的
射击成绩的中位数为____环.
7.5
7.样本数据3,,4, ,8的平均数是5,众数是3,则这组数据的中位
数是___.
4
8.某企业加强了管理,准备采取每天的任务定额和超产有奖的措施,以
提高工作效率.下面是该企业10名员工过去一天中各自装配机器的数量
(单位:台):6,8,16,14,11,10,6,13,10,6.
(1)求这组数据的平均数、众数和中位数.
解:平均数是
;
将这组数据从小到大排列为6,6,6,8,10,10,11,13,14,16,
则中位数是 ;
数据6出现次数最多, 众数是6.
(2)管理者为了提高员工的工作效率,又不能挫伤其积极性,应确定
每名员工的标准日产量为多少台比较恰当?
解:管理者应确定每名员工的标准日产量为10台比较恰当.
考点2 方差
9.[2024 雅安] 某校开展了红色经典故事演讲比赛,其中8名同学的成绩
(单位:分)分别为85,81,82,86,82,83,92,89.关于这组数据,
下列说法中正确的是( )
D
A.众数是92 B.中位数是84.5 C.平均数是84 D.方差是13
10.[2024 云南] 甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人
10次射击成绩的平均数(单位:环)和方差 如下表所示:
甲 乙 丙 丁
9.9 9.5 8.2 8.5
0.09 0.65 0.16 2.85
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应
该选择( )
A
A.甲 B.乙 C.丙 D.丁
11.如图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名
同学的成绩,下列说法正确的是( )
D
A.甲同学成绩的平均分高,波动较小
B.甲同学成绩的平均分高,波动较大
C.乙同学成绩的平均分高,波动较小
D.乙同学成绩的平均分高,波动较大
谢谢观看!
章末复习
第二十章 数据的分析
人教版(2024)数学八年级下册
授课教师:********
班 级:********
时 间:********
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
算术平均数
概念
拓展
=(x1+x2+ +xn).
① nx1,nx2,…,nxn的平均数为n;
② x1+b,x2+b,…,xn+b的平均数为+b;
③ nx1+b,nx2+b,…,nxn+b的平均数为n+b.
知识梳理
加权平均数
计算
方法
算术平均数和加权平均数的区别与联系.
=
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当考察的对象很多,或对考察对象带有破坏性时适用.
中位数
概念
注意
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
①按照大小顺序排列;
②可能是这组数据中的某个数,也可能不是这组数据中的数.
众数
概念
注意
一组数据中出现次数最多的数据称为这组数据的众数.
众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
1. 算术平均数
一般地,如果有 n 个数 x1,x2, ,xn,那么我们把(x1+x2+ +xn)叫做这 n 个数的算术平均数,简称平均数,记作 ,读作 x拔,则有 =(x1+x2+ +xn).
2. 加权平均数
一般地,如果有 n 个数 x1,x2, ,xn 的权分别为 w1,w2, ,wn,那么我们把叫做这n个数的加权平均数.
在求 n 个数的平均数时,如果 x1 出现 f1 次, x2 出现 f2 次, , xk 出现 fk 次(这里的 f1+ f2+ +fk =n),那么这 n 个数的平均数 = .也叫做 x1,x2, ,xk 这 k 个数的加权平均数,其中 f1, f2, , fk分别叫做 x1,x2, ,xk 的权.
3. 用样本平均数估计总体平均数
(1)组中值:数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
(2)用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
4. 中位数
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
5. 众数
一组数据中出现次数最多的数据称为这组数据的众数.
注意:众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
方差
计算公式
意义
+….
方差越大,数据的波动越大;方差越小,数据的波动越小.
知识梳理
方差
估算
意义
用样本的方差估计总体的方差.
根据方差的大小来判断总体的稳定情况.
1. 方差
设有 n 个数据 x1,x2, ,xn,各数据与它们的平均数 的差的平方分别是,,
我们用这些值的平均数,即用+
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作 .
2. 方差的意义
方差可以反映数据的波动程度,即:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
3. 用样本方差估计总体方差
用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
1.求下列数据的方差.
2,3,5,7,7,6
解:
重点解析
求数据的方差,先求出数据的平均数.
重难点1:方差的计算
一、核心知识巩固
考点1 平均数、中位数、众数
1.[2024 湖南] 某班的5名同学1分钟跳绳的成绩(单位:次)分别为:
179,130,192,158,141.这组数据的中位数是( )
B
A.130 B.158 C.160 D.192
2.[2024 无锡] 一组数据:31,32,35,37,35,这组数据的平均数和
中位数分别是( )
C
A.34,34 B.35,35 C.34,35 D.35,34
3.[2024 扬州] 第8个全国近视防控宣传教育月的主题是“有效减少近视
发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学
视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 4 4 7 11 10 5 3
这45名同学视力检查数据的众数是( )
B
A.4.6 B.4.7 C.4.8 D.4.9
4.[2024 南京鼓楼区一模] 如图为某班35名学
生投篮成绩的条形统计图,其中上面部分数据
破损导致数据不完全.已知此班学生投篮成绩
的中位数是5,则根据下图,无法确定下列哪
一选项中的数值( )
C
A.4球以下的人数 B.5球以下的人数
C.6球以下的人数 D.7球以下的人数
(第5题)
5. 某校拟招聘一名优秀的数学教师,
设置了笔试、面试、试讲三项水平测试,综合成绩
按照笔试占,面试占,试讲占 进行计
算,小徐的三项测试成绩如图所示,则她的综合成
绩为_____分.
85.8
(第6题)
6.[2024 镇江] 小丽6次射击的成绩如图所示,则她的
射击成绩的中位数为____环.
7.5
7.样本数据3,,4, ,8的平均数是5,众数是3,则这组数据的中位
数是___.
4
8.某企业加强了管理,准备采取每天的任务定额和超产有奖的措施,以
提高工作效率.下面是该企业10名员工过去一天中各自装配机器的数量
(单位:台):6,8,16,14,11,10,6,13,10,6.
(1)求这组数据的平均数、众数和中位数.
解:平均数是
;
将这组数据从小到大排列为6,6,6,8,10,10,11,13,14,16,
则中位数是 ;
数据6出现次数最多, 众数是6.
(2)管理者为了提高员工的工作效率,又不能挫伤其积极性,应确定
每名员工的标准日产量为多少台比较恰当?
解:管理者应确定每名员工的标准日产量为10台比较恰当.
考点2 方差
9.[2024 雅安] 某校开展了红色经典故事演讲比赛,其中8名同学的成绩
(单位:分)分别为85,81,82,86,82,83,92,89.关于这组数据,
下列说法中正确的是( )
D
A.众数是92 B.中位数是84.5 C.平均数是84 D.方差是13
10.[2024 云南] 甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人
10次射击成绩的平均数(单位:环)和方差 如下表所示:
甲 乙 丙 丁
9.9 9.5 8.2 8.5
0.09 0.65 0.16 2.85
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应
该选择( )
A
A.甲 B.乙 C.丙 D.丁
11.如图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名
同学的成绩,下列说法正确的是( )
D
A.甲同学成绩的平均分高,波动较小
B.甲同学成绩的平均分高,波动较大
C.乙同学成绩的平均分高,波动较小
D.乙同学成绩的平均分高,波动较大
谢谢观看!
