2025年九年级数学中考三轮冲刺训练二次函数定值定点问题(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练二次函数定值定点问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 21:08:09 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练二次函数定值定点问题
1.综合与探究:
如图1,在平面直角坐标系中,抛物线y=ax2﹣2x+c与x轴交于点A(﹣3,0)和点C,与y轴交于点B(0,3),点P是抛物线上点A与点C之间的动点(不包括点A,点C).
(1)求抛物线的解析式;
(2)如图1,动点P在抛物线上,且在直线AB上方,求△ABP面积的最大值及此时点P的坐标;
(3)如图2,过原点O作直线l交抛物线于M、N两点,点M的横坐标为m,点N的横坐标为n.求证:mn是一个定值.
2.已知二次函数y=ax2+6的图象经过点P(4,2),直线AB与抛物线相交于A、B两点.
(1)求抛物线的解析式;
(2)如图1,若直线AB的解析式为y=kx﹣4k﹣3,且△PAB的面积为35,求k的值;
(3)如图2,若∠APB=90°,则直线AB必经过一个定点C,求点C的坐标.
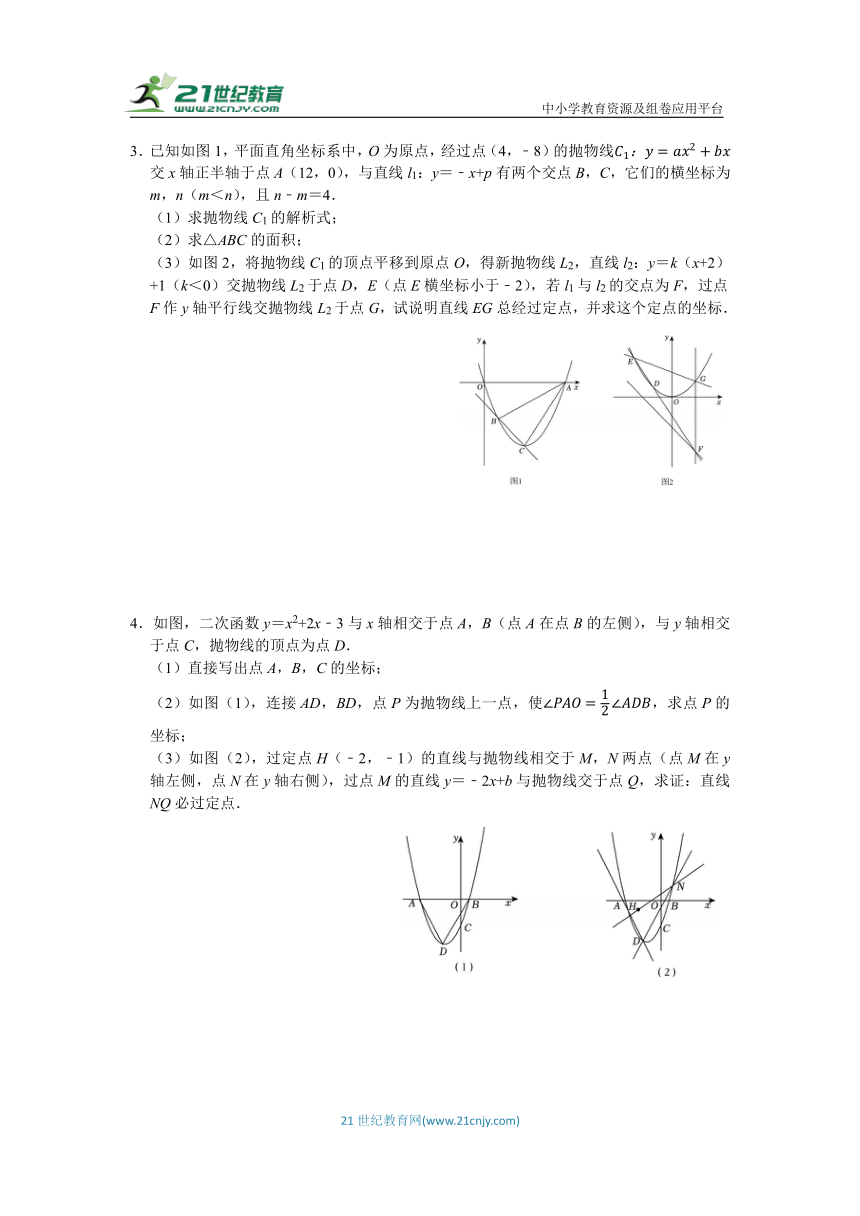
3.已知如图1,平面直角坐标系中,O为原点,经过点(4,﹣8)的抛物线交x轴正半轴于点A(12,0),与直线l1:y=﹣x+p有两个交点B,C,它们的横坐标为m,n(m<n),且n﹣m=4.
(1)求抛物线C1的解析式;
(2)求△ABC的面积;
(3)如图2,将抛物线C1的顶点平移到原点O,得新抛物线L2,直线l2:y=k(x+2)+1(k<0)交抛物线L2于点D,E(点E横坐标小于﹣2),若l1与l2的交点为F,过点F作y轴平行线交抛物线L2于点G,试说明直线EG总经过定点,并求这个定点的坐标.
4.如图,二次函数y=x2+2x﹣3与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,抛物线的顶点为点D.
(1)直接写出点A,B,C的坐标;
(2)如图(1),连接AD,BD,点P为抛物线上一点,使,求点P的坐标;
(3)如图(2),过定点H(﹣2,﹣1)的直线与抛物线相交于M,N两点(点M在y轴左侧,点N在y轴右侧),过点M的直线y=﹣2x+b与抛物线交于点Q,求证:直线NQ必过定点.
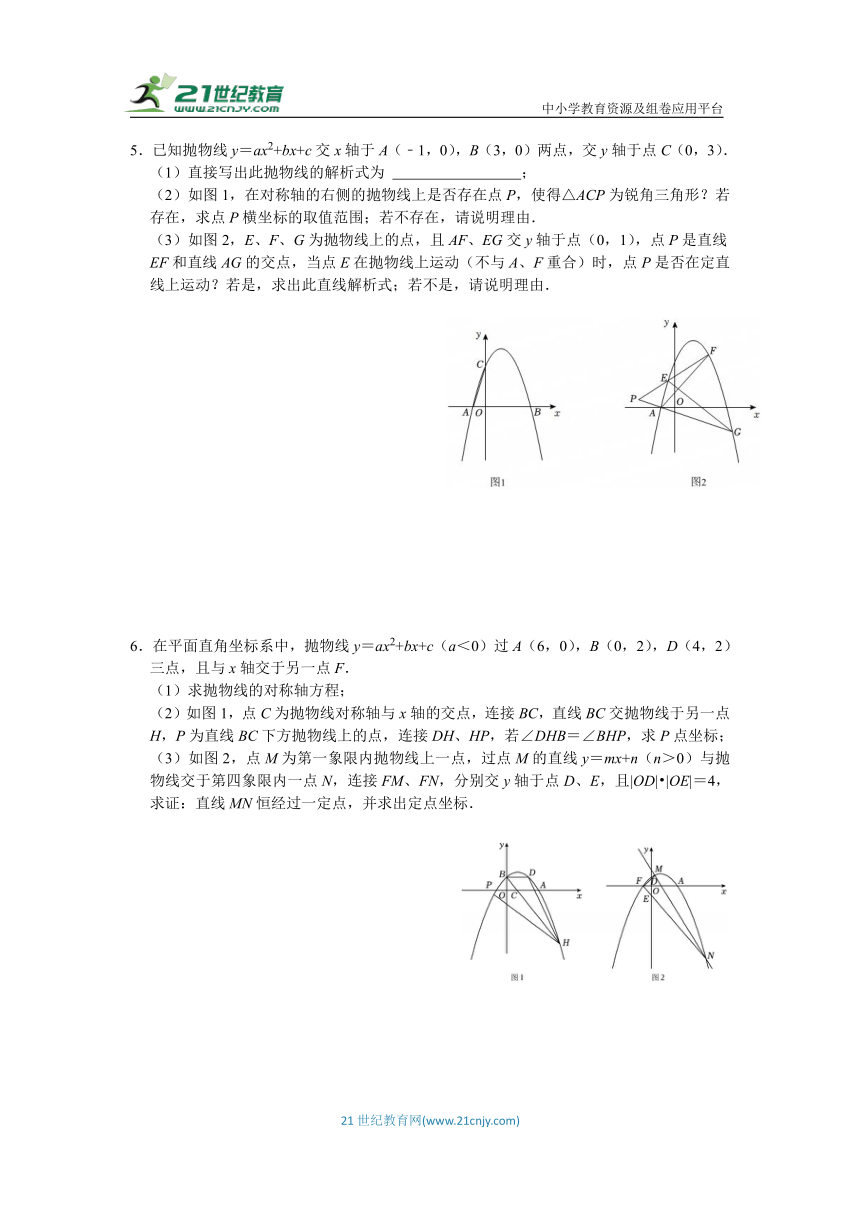
5.已知抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C(0,3).
(1)直接写出此抛物线的解析式为 ;
(2)如图1,在对称轴的右侧的抛物线上是否存在点P,使得△ACP为锐角三角形?若存在,求点P横坐标的取值范围;若不存在,请说明理由.
(3)如图2,E、F、G为抛物线上的点,且AF、EG交y轴于点(0,1),点P是直线EF和直线AG的交点,当点E在抛物线上运动(不与A、F重合)时,点P是否在定直线上运动?若是,求出此直线解析式;若不是,请说明理由.
6.在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)过A(6,0),B(0,2),D(4,2)三点,且与x轴交于另一点F.
(1)求抛物线的对称轴方程;
(2)如图1,点C为抛物线对称轴与x轴的交点,连接BC,直线BC交抛物线于另一点H,P为直线BC下方抛物线上的点,连接DH、HP,若∠DHB=∠BHP,求P点坐标;
(3)如图2,点M为第一象限内抛物线上一点,过点M的直线y=mx+n(n>0)与抛物线交于第四象限内一点N,连接FM、FN,分别交y轴于点D、E,且|OD| |OE|=4,求证:直线MN恒经过一定点,并求出定点坐标.
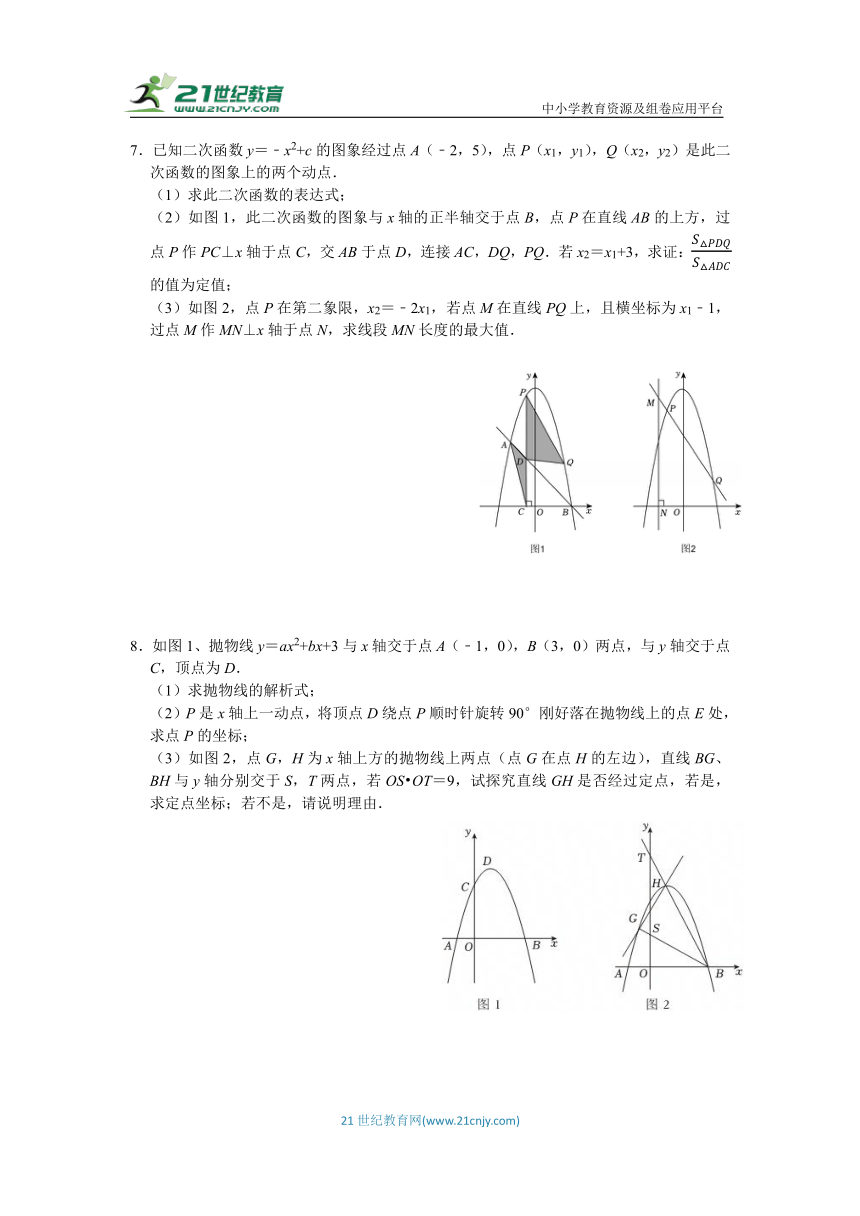
7.已知二次函数y=﹣x2+c的图象经过点A(﹣2,5),点P(x1,y1),Q(x2,y2)是此二次函数的图象上的两个动点.
(1)求此二次函数的表达式;
(2)如图1,此二次函数的图象与x轴的正半轴交于点B,点P在直线AB的上方,过点P作PC⊥x轴于点C,交AB于点D,连接AC,DQ,PQ.若x2=x1+3,求证:的值为定值;
(3)如图2,点P在第二象限,x2=﹣2x1,若点M在直线PQ上,且横坐标为x1﹣1,过点M作MN⊥x轴于点N,求线段MN长度的最大值.
8.如图1、抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求抛物线的解析式;
(2)P是x轴上一动点,将顶点D绕点P顺时针旋转90°刚好落在抛物线上的点E处,求点P的坐标;
(3)如图2,点G,H为x轴上方的抛物线上两点(点G在点H的左边),直线BG、BH与y轴分别交于S,T两点,若OS OT=9,试探究直线GH是否经过定点,若是,求定点坐标;若不是,请说明理由.
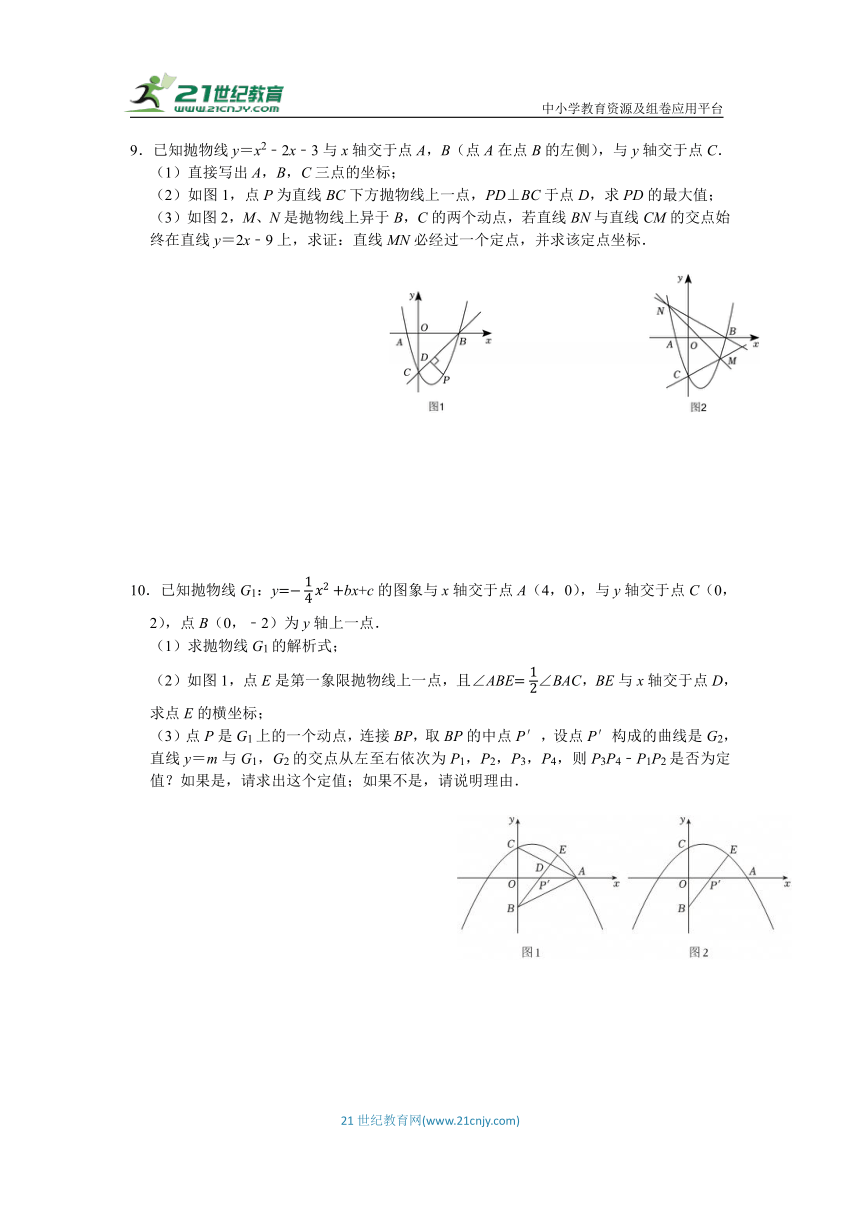
9.已知抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)直接写出A,B,C三点的坐标;
(2)如图1,点P为直线BC下方抛物线上一点,PD⊥BC于点D,求PD的最大值;
(3)如图2,M、N是抛物线上异于B,C的两个动点,若直线BN与直线CM的交点始终在直线y=2x﹣9上,求证:直线MN必经过一个定点,并求该定点坐标.
10.已知抛物线G1:ybx+c的图象与x轴交于点A(4,0),与y轴交于点C(0,2),点B(0,﹣2)为y轴上一点.
(1)求抛物线G1的解析式;
(2)如图1,点E是第一象限抛物线上一点,且∠ABE∠BAC,BE与x轴交于点D,求点E的横坐标;
(3)点P是G1上的一个动点,连接BP,取BP的中点P′,设点P′构成的曲线是G2,直线y=m与G1,G2的交点从左至右依次为P1,P2,P3,P4,则P3P4﹣P1P2是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
11.抛物线y=ax2+2ax+3(a<0)交x轴于A,B两点(A在B左边),交y轴于点C.
(1)直接写出抛物线的对称轴;
(2)已知AB=4.
①如图1,点D在第二象限抛物线上,BD交AC于点E.若BE=2DE,求点D的坐标;
②如图2,过点T(﹣1,t)(t>0)分别作直线l1:y=k1x+b1(k1>0)和直线l2:y=k2x+b2(k2<0),直线l1交抛物线于F,G两点,直线l2交抛物线于M,N两点.设线段FG,MN的中点分别为P,Q,若k1 k2=﹣2t,且k1+k2≠0,求证:直线PQ必经过一定点.
12.如图1,已知二次函数y=x2+bx+c的图象与x轴交于点A(﹣4,0)和点B,与y轴的负半轴交于点C(0,﹣4).
(1)求这个函数的解析式;
(2)点P是抛物线上的一点,当∠BCP=45°时,求点P的坐标;
(3)如图2,将直线AC向下平移与抛物线交于M、N两点,直线AM、CN交于Q点,请问点Q的横坐标是否为定值,并说明理由.
13.如图1,已知y=ax2﹣bx﹣3a过点A(﹣3,0)和点C(0,3).
(1)求此抛物线的解析式;
(2)在第一象限抛物线上是否存在一点P,使得∠PAB+∠BCO=45°,请求出P点的坐标;
(3)如图2所示,对称轴交x轴于点M,顶点为点D,在第二象限抛物线上有一动点Q,直线AQ,BQ与对称轴分别相交于点E、F,当点Q运动时,试探究的值是否为一个定值,若是,求出该定值;若不是,说明理由.
14.抛物线y=x2﹣6x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
(1)直接写出点B和点D的坐标;
(2)如图1,连接OD,P为x轴上的动点,当时,求点P的坐标;
(3)如图2,将抛物线y=x2﹣6x沿x轴水平向左平移a个单位(a>0),新的抛物线与x轴交于E,F两点.点M为第一象限抛物线上的一个动点,连接EM,作EM关于x轴对称的直线EN交抛物线于点N,连接MN,过F点作y轴的平行线HF交MN于点H,当M点运动时,的值是否变化?若不变,求出它的值;若变化,说明理由.
15.已知抛物线L:y=x2﹣2mx+m2﹣m+1(m为常数),顶点为M.
(1)求M的坐标(用含m的式子表示);
(2)若抛物线L与直线y=x有唯一公共点P,求PM的长.
(3)如图,若抛物线L的对称轴为y轴,顶点为C,过y轴正半轴上一定点F(点F在点C上方)的任意直线交抛物线L于点A,B,分别过点A,B作x轴的垂线,垂足分别为点D,E,连OA,OB.
①直接写出抛物线L的解析式;
②若记△AOB,△AOD,△BOE的面积分别为S1,S2,S3,当为定值时,求定点F坐标.
参考答案
1.【解答】(1)解:在平面直角坐标系中,抛物线y=ax2﹣2x+c与x轴交于点A(﹣3,0)和点C,与y轴交于点B(0,3),把点A(﹣3,0)和点B(0,3)的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)解:如下图所示,过点P作PH∥y轴,交AB于点H,
设直线AB的解析式为y=kx+b,把点A和点B的坐标代入得:
,
解得:,
∴直线AB的解析式为y=x+3,
点P是抛物线上点A与点C之间的动点(不包括点A,点C).设点P的横坐标为x,则点P的纵坐标为﹣x2﹣2x+3,
∴点H的横坐标为x,点H的纵坐标为x+3,
∴PH=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x,
∵S△APB=S△APH+S△BPH,
整理得:S△APBx,
∴可知当时,△APB的面积有最大值,最大值是,
当时,,
此时点P的坐标为;
(3)证明:设直线MN的解析式为y=hx,
解方程组,
可得:﹣x2﹣2x+3=hx,
整理得:x2+(2+h)x﹣3=0,
一元二次方程x2+(2+h)x﹣3=0中,
Δ=b2﹣4ac=(2+h)2+12>0,
∴一元二次方程x2+(2+h)x﹣3=0有两个不相等的实数根,
这两个不相等的实数根分别为m、n,
则有,
∴mn是一个定值.
2.【解答】解:(1)∵二次函数y=ax2+6的图象经过点P(4,2),
∴16a+6=2,
解得a,
∴抛物线的解析式为:yx2+6;
(2)已知直线AB的解析式为y=kx﹣4k﹣3,
令x=4,则y=﹣3,
∴直线AB过定点D(4,﹣3),
∵P(4,2),
∴PD∥y轴,PD=5,
∴S△ABP PD |xB﹣xA|=35,
∴|xB﹣xA|=14,
令x2+6=kx﹣4k﹣3,整理得x2+4kx﹣16k﹣36=0,
∴xB+xA=﹣4k,xB xA=﹣16k﹣36,
∴|xB﹣xA|2=(xB+xA)2﹣4xB xA=142,
整理得16k2+64k﹣52=0,
解得k=﹣2或k=﹣2;
(3)设A(m,m2+6),B(n,n2+6),如图2,过点P作直线PN∥x轴,分别过A、B两点作PN的垂线,垂足分别为N、M,
∵∠APB=90°,△PAN∽△BPM,
∴AN:PM=PN:BM,
∴,即,
∴(m+4)(n+4)=﹣16,
∴mn+4(m+n)+32=0①,
联立方程组,
∴x2+tx+b﹣6=0,
∴m+n=﹣4t,mn=4b﹣24②,
将②代入①,得化简,得
b=4t﹣2,
∴直线AB的解析式为y=tx+4t﹣2,即y=t(x+4)﹣2,
∴直线AB经过定点C(﹣4,﹣2).
3.【解答】解:(1)∵抛物线经过点(4,﹣8)和点(12,0),
∴,
解得:,
∴抛物线C1的解析式为yx2﹣3x;
(2)∵抛物线与直线l1:y=﹣x+p有两个交点B,C,它们的横坐标为m,n(m<n),
联立得:x2﹣3x=﹣x+p,
整理得:x2﹣8x﹣4p=0,
∴m+n=8,
又∵n﹣m=4,
∴m=2,n=6,
∴B(2,﹣5),C(6,﹣9),
把B(2,﹣5)代入y=﹣x+p,得:﹣5=﹣2+p,
解得:p=﹣3,
∴直线l1:y=﹣x﹣3,
当y=0时,﹣x﹣3=0,
解得:x=﹣3,
∴直线l1:y=﹣x﹣3与x轴交于点M(﹣3,0),如图,
∵A(12,0),B(2,﹣5),C(6,﹣9),
∴AM=12﹣(﹣3)=15,
∴S△ABC=S△ACM﹣S△ABMAM |yC|AM |yB|15×915×5=30;
(3)∵抛物线C1:yx2﹣3x(x﹣6)2﹣9,顶点坐标为(6,﹣9),将抛物线C1的顶点平移到原点O,得新抛物线L2,
∴新抛物线L2:yx2,
联立直线l2与新抛物线的解析式,得x2=k(x+2)+1,
解得:xD=﹣2,xE=4k+2,
联立直线l1与l2的解析式,得:k(x+2)+1=﹣x﹣3,
解得:x,
∵FG∥y轴,交抛物线L2于点G,
∴G(,),
设直线EG的解析式为:y=k′x+b′,则x2=k′x+b′,
整理得:x2﹣4k′x﹣4b′=0,
∴xE+xG=4k′,xE xG=﹣4b′,
∴k′(xE+xG)(4k+2),
b′xE xG(4k+2)(),
∴直线EG的解析式为yx,
当x=﹣2时,y(﹣2)3,
∴直线EG经过定点(﹣2,3).
4.【解答】(1)对于y=x2+2x﹣3,当x=0时,y=﹣3,令y=0,则x=1或﹣3,
则点A、B、C的坐标分别为:(﹣3,0)、(1,0)、(0,﹣3);
(2)由抛物线的表达式知,点D(﹣1,﹣4),
过点D作DE∥y轴交x轴于点E,
由函数的对称性值,∠ADE∠ADB,
由点A、D的坐标得,tan∠ADEtan∠PAO,
则直线PA的表达式为:y=±(x+3),
联立上式和抛物线的表达式得:x2+2x﹣3±(x+3),
解得:x=﹣3(舍去)或或,
即点P(,)或(,);
(3)证明:设M(p,p2+2p﹣3),N(q,q2+2q﹣3),
由点M、N的坐标得,直线MN解析式为y=(p+q+2)x﹣pq+3,
∵直线MN过定点(﹣2,﹣1),
∴﹣2(p+q+2)﹣pq﹣3=﹣1,
∴pq=﹣2p﹣2q+6,
∵直线y=﹣2x+b过M(p,p2+2p﹣3),
∴P2+2P﹣3=﹣2P+b,
∴b=P2+4q﹣3,
∴y=﹣2x﹣P2+4P﹣3,
由﹣2x﹣P2+4P﹣3=﹣x2+2x+3得:x=P或x=﹣P﹣4,
∴G(﹣P﹣4,P2+6P+5),
由N、Q的坐标得,直线NQ解析式为y=(﹣p﹣4+q+2)x﹣(﹣p﹣4)q﹣3,
∵pq=﹣2p﹣2q+6,
则y=(﹣p+q﹣2)x﹣2p+2q﹣9,
当x=﹣2时,y=﹣2(﹣p+q﹣2)﹣2p+2q﹣9=﹣5,
∴直线MG必过定点(﹣2,﹣5).
5.【解答】解:(1)由题意可设交点式y=a(x+1)(x﹣3),代入(0,3),得3=a×1×(﹣3),解得a=﹣1,
∴此抛物线的解析式为y=﹣x2+2x+3,
故答案为:y=﹣x2+2x+3;
(2)存在点P,使得△ACP为锐角三角形,理由如下:
作P'C⊥AC于点C交抛物线于点P',过点C作DE∥x轴,P'E⊥DE于点E,AD⊥DE于点D,如图1所示,
设P'(m,﹣m2+2m+3),
∵∠DCA+∠ECP'=90°,∠DCA+∠DAC=90°,
∴∠ECP'=∠DAC,
从而tan∠ECP'=tan∠DAC,即,
∴,解得m或0(舍去);
作P''A⊥CA于点A交抛物线于点P'',作P''F⊥DA的延长线于点F,
设P''(m,﹣m2+2m+3),
同理可证tan∠AP''F=tan∠DAC,即,
∴,解得m,
故点P横坐标的取值范围为.
(3)解法一(点参法):
∵A(﹣1,0),H(0,1),
∴由待定系数法可得直线AG的解析式为y=x+1,
与抛物线y=﹣x2+2x+3联立可得x+1=﹣x2+2x+3,解得xF=2,
故F(2,3).
设E(m,﹣m2+2m+3),G(n,﹣n2+2n+3),A(﹣1,0),
则由待定系数法可得直线EG的解析式为y=(2﹣m﹣n)x+3+mn,
∵直线EG过点H(0,1),
∴1=3+mn,mn=﹣2,
同理得直线AG的解析式为y=(3﹣n)x+3﹣n,
直线EF的解析式为y=﹣mx+2m+3,
联立直线AG与直线EF得﹣mx+2m+3=(3﹣n)x+3﹣n,
得x,即xP,
∴yP=(3﹣n)(x+1)
=(3﹣n)
=5+2xP.
故点P在直线y=2x+5上.
解法二(线参法):
∵直线EF过点F(2,3),直线AG过点A(﹣1,0),
故设直线EF解析式为y=k(x﹣2)+3,直线AG解析式为y=m(x+1),
联立直线EF和抛物线y=﹣x2+2x+3,可得x2+(k﹣2)x﹣2k=0,由韦达定理知xE+2=2﹣k,
故xE=﹣k,则E(﹣k,﹣k2﹣2k+3),
联立直线AG与抛物线y=﹣x2+2x+3,可得x2+(m﹣2)x+m﹣3=0,由韦达定理知xG+(﹣1)=2﹣m,
故xG=3﹣m,则G(3﹣m,﹣m2+4m),
由待定系数法可得直线EG的解析式为y=(k+m﹣1)x+k(m﹣3)+3,
又∵直线EG过点H(0,1),
则k(m﹣3)+3=1,即km=3k﹣2,
联立直线EF与直线AG,可得(k﹣m)x=m+2k﹣3,解得x,
即xP,
故yP=m(x+1)
=m
=5+2xP,
故点P在直线y=2x+5上.
6.【解答】解:(1)∵抛物线y=ax2+bx+c过B(0,2),D(4,2),
∴抛物线的对称轴方程为直线x.
(2)∵对称轴为直线x,
∴b=﹣4a,
∴抛物线y=ax2﹣4ax+2,代入点A(6,0),得6a=﹣1,
解得a,
∴抛物线解析式为yx2x+2.
∵点C为抛物线对称轴与x轴的交点,
∴C(2,0),
又∵B(0,2),
由待定系数法可知直线BC的解析式为y=﹣x+2,
联立y=﹣x+2与yx2x+2,得x2﹣10x=0,
解得x=10或0(舍去),
即H(10,﹣8).
如图1所示,设PH交y轴于点F,
∵OB=OC=2,
∴∠OBC=∠OCB=45°,
∵BD∥OC,
∴∠DBC=∠OCB=45°,
当∠DHB=∠BHP时,
在△BFH和△BDH中,
∵,
∴△BFH≌△BDH(ASA),
∴BF=BD=4,
故F(0,﹣2),
则由待定系数法可得直线HF的解析式为y,
联立直线HF解析式与抛物线解析式可得5x2﹣38x﹣120=0,
解得x=10或,
故P点坐标为(,).
(3)证明:如图2所示,设M(m,),N(n,),
故由待定系数法可得直线MN的解析式为y=[(m+n)]x2.
∵A(6,0),再由抛物线对称性可知F(﹣2,0),
同理可得直线FM的解析式为y=[(m﹣2)]x+2,
则OD2,
同理可得直线FN的解析式为y=[(n﹣2)]x+2,
则OE,
∵|OD| |OE|=4,即(2)()=4,化简整理可得(6﹣m)(n﹣6)=36,
进而可得mn=6(m+n)﹣72①,
把①式代入直线MN的解析式中,得:
y=[(m+n)]x2
=[(m+n)]x
,
令,解得x=6,此时y=﹣6,
故直线MN恒过定点(6,﹣6).
7.【解答】(1)解:将点A的坐标代入抛物线表达式得:5=﹣4+c,
则c=9,
即抛物线的表达式为:y=﹣x2+9;
(2)证明:令y=﹣x2+9,则x=±3,则点B(3,0),
由点A、B的坐标得,直线AB的表达式为:y=﹣x+3,
设点P、Q、D的表达式分别为:(x1,9)、(x2,9)、(x1,﹣x1+3),
则S△PDQPD×(xQ﹣xP)(9+x1﹣3)(x2﹣x1)(x1+6),
同理可得:S△ADCCD×(xD﹣xA)(x1+6),
则3为定值;
(3)解:点P、Q的坐标分别为:(x1,9)、(﹣2x1,﹣49),
由点P、Q的坐标得,直线PQ的表达式为:y=x1(x﹣x1)9=xx1﹣29,
则MN=yM=(x1﹣1)x1﹣29=﹣(x1)2,
故MN的最大值为:.
8.【解答】解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0)两点,
∴,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)设P(t,0),过点E作EF⊥x轴于点F,设抛物线的对称轴交x轴于点K,如图1,
则∠DKP=∠PFE=90°,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4),K(1,0),
∴PK=1﹣t,DK=4,
设E(e,﹣e2+2e+3),则F(e,0),
∴EF=﹣(﹣e2+2e+3)=e2﹣2e﹣3,PF=e﹣t,
由旋转得:PE=PD,∠DPE=90°,
∴∠DPK+∠EPF=90°,
∵∠DPK+∠PDK=90°,
∴∠EPF=∠PDK,
∴△PEF≌△DPK(AAS),
∴EF=PK,PF=DK,
∴,
解得:,,
∴点P的坐标为(,0)或(,0);
(3)直线GH经过定点(﹣1,1).理由如下:
设G(m,﹣m2+2m+3),H(n,﹣n2+2n+3),
设直线GH的解析式为y=kx+d,则,
解得:,
∴直线GH的解析式为y=(﹣m﹣n+2)x+mn+3,
同理可得:直线BG的解析式为y=﹣(m+1)(x﹣3),
直线BH的解析式为y=﹣(n+1)(x﹣3),
令x=0,则yS=3(m+1),yT=3(n+1),
∴OS=3(m+1),OT=3(n+1),
∵OS OT=9,
∴3(m+1)×3(n+1)=9,
∴m+n=﹣mn,
代入直线GH的解析式得y=(mn+2)x+mn+3,
∵当x=﹣1时,y=1,
∴直线GH经过定点(﹣1,1).
9.【解答】(1)解:对于y=x2﹣2x﹣3,令y=0,则0=x2﹣2x﹣3,
∴x1=﹣1,x2=3,
∴点A(﹣1,0),点B(3,0),
令x=0,则y=﹣3,
∴点C(0,﹣3);
(2)解:过点P作PE⊥x轴于E,交BC于点F,如图1:
设直线BC的解析式为y=kx+b,
将点B(3,0),C(0,﹣3)代入y=kx+b得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
设P(x,x2﹣2x﹣3),则F(x,x﹣3),
∴PF=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∵PE⊥x轴,
∴PE∥y轴,
∴∠PFD=∠BCO,
∵∠PDF=∠BOC=90°,
∴△PDF∽△BCO,
∴,
∵B(3,0),C(0,﹣3),
∴OB=3,OC=3,
∴BC=3,
∴,
∴PDx2x,
∴当x时,PD最大为;
(3)证明:如图2,设点M(xM,yM),N(xN,yN),
直线MN:y=k′x+b′,直线CM:y=k1x+b1,直线BN:y=k2x+b2,
将点C(0,﹣3)代入直线CM的解析式得:b1=﹣3,
将点B(3,0)代入直线BN的解析式得:b2=﹣3k2,
联立直线MN与抛物线的解析式得:,
整理得:x2﹣(k′+2)x﹣b′﹣3=0,
则xM+xN=k′+2,xM xN=﹣b′﹣3,
同理:xM+xC=k1+2,xN+xB=k2+2,
∵xC=0,xB=3,
∴xM=k1+2,xN=k2﹣1,
∴k′=xM+xN﹣2=k1+2+k2﹣1﹣2=k1+k2﹣1,
b′=﹣xM xN﹣3=﹣(k1+2)(k2﹣1)﹣3=﹣k1k2﹣2k2+k1+2﹣3=﹣k1k2﹣2k2+k1﹣1,
联立直线CM与直线BN的解析式得:,
解得:,
∵直线BN与直线CM的交点始终在直线y=2x﹣9上,
∴29,
化简得:k1k2=3k1﹣2,
∴b′=﹣k1k2﹣2k2+k1﹣1=﹣3k1+2﹣2k2+k1﹣1=﹣2k1﹣2k2+1=﹣2(k1+k2)+1=﹣2(k′+1)+1=﹣2k′﹣1,
∴直线MN:y=k′x﹣2k′﹣1=k′(x﹣2)﹣1,
∴不论k′为何值,均有x=2时,y=﹣1,
即:直线MN恒过定点P(2,﹣1).
10.【解答】解:(1)将点A(4,0),C(0,2)代入抛物线G1,
得到,
解得,
∴抛物线G1的解析式为,
(2)∵A(4,0),B(0,﹣2),C(0,2),
∴OA=4,OB=OC=2,
又∵OA⊥BC,
∴AC=AB,
∴OA平分∠BAC,
∵,
∴∠ABE=∠OAB,
∴BD=AD,
设OD=m,则AD=BD=4﹣m,
在Rt△OBD中,OD2+OB2=BD2,
∴m2+22=(4﹣m)2,
解得,,
∴,
设直线BD解析式为y=kx﹣2,代入点D,则,
解得,
∴直线BD解析式为,
联立抛物线G1与直线BD,
∴,
得,x2=﹣6(舍去),
∴点E的横坐标为;
(3)P3P4﹣P1P2为定值,理由如下:
设点P′(x,y),作P′M⊥y轴于M,作PN⊥y轴于N,则P′M∥PN,M(0,y),如图2,
又∵P′为PB中点,
∴P′M为△PBM中位线,
∴PN=2P′M,M为BN中点,
∴xP=2x,yP﹣y=y﹣(﹣2),
∴yP=2y+2,
∴P(2x,2y+2),
将点P代入抛物线G1,
∴,
化简得,
设P1,P2,P3,P4的横坐标分别为x1,x2,x3,x4,
则P3P4﹣P1P2=(x4﹣x3)﹣(x2﹣x1)=(x4+x1)﹣(x2+x3),
由得x4+x1=2,
由得x2+x3=1,
∴P3P4﹣P1P2=2﹣1=1定值.
11.【解答】解:(1)∵y=ax2+2ax+3
∴抛物线的对称轴为:直线 x1;
(2)①过点D作DP∥y轴交AC于点P,过点B作BQ∥y轴交AC的延长线于点Q.
∴DP∥BQ,
∴△DPE∽△BQE,
∴,
∵BE=2DE,
∴BQ=2DP,
∵AB=4,抛物线的对称轴为直线 x=﹣1,
∴A(﹣3,0),B(1,0),C(0,3),
∴a=﹣1,AC:y=x+3,
∴Q(1,4),
∴BQ=4,DP=2,
设D(t,﹣t2﹣2t+3),则P(t,﹣t2﹣2t+1),
∵直线y=x+3经过点P,
∴t+3=﹣t2﹣2t+1,
解得:t1=﹣1,t2=﹣2,
∴D点的坐标为(﹣1,4)或 (﹣2,3);
②联立得x2+(k1+2)x+b1﹣3=0,
∴xF+xG=﹣k1﹣2,
∴,
联立得x2+(k2+2)x+b2﹣3=0,
同理可得:,
∵l1,l2经过点T(﹣1,t),
∴﹣k1+b1=t,﹣k2+b2=t,
即:b1=k1+t,b2=k2+t,
∴l1:y=k1x+k1+t+t,l2:y=k2x+k2+t,
∴,Q(),
∵k1 k2=﹣2t,
设直线PQ的解析式为y=kx+b,则,
解得:,
∴直线PQ的解析式为y=(k1+k2)x+(k1+k2),
∴直线PQ恒过定点(﹣1,0).
12.【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=x2+3x﹣4①;
(2)由抛物线的表达式知,点B(1,0),
则tan∠OBC=4,
设直线CP交x轴于点H,过点H作HN⊥BC于点N,
在△BCH中,BC,
设HN=4x=CN,则HN=x,
则BHx,BC=BN+CN=5x,
则x,则BHx,
则点H(,0),
由点C、H得,直线CH的表达式为:yx﹣4②,
联立①②得:x2+3x﹣4x﹣4,
解得:x=0(舍去)或,
则点P(,);
(3)由点A、C的坐标得,直线AC的表达式为:y=﹣x﹣3,
则设直线MN的表达式为:y=﹣x+t③,
联立①③并整理得:x2+4x﹣(t+4)=0,
则m+n=﹣4,
设点M、N的坐标分别为:(m,m2+3m﹣4)、(n,n2+3n﹣4),
由点A、M得,直线AM的表达式为:y=(m﹣1)(x+4),
同理可得,直线CN的表达式为:y=(n+3)x﹣4,
联立上述两式得:(m﹣1)(x+4)=(n+3)x﹣4,
解得:x2.
即Q的横坐标是否为定值,为﹣2.
13.【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2﹣2x+3;
(2)设直线AP交y轴于点H,过点H作HN⊥AC于点N,
在Rt△OCB中,tan∠OCB,
由OC=OA=3知,∠ACH=45°=∠CAO,
∵∠HAO+∠CAO=45°,∠PAB+∠BCO=45°,
∴∠CAH=∠OCB,则tan∠CAH=tan∠OCB,
在△ACH中,∠ACH=45°,tan∠CAH=tan∠OCB,AC=3,
故设NH=x=CN,则AH=3x,CHx,
则AC=4x=3,则x,
则CHx,则点H(0,),
由点A、H的坐标得,直线AH的表达式为:yx,
联立上式和抛物线的表达式得:﹣x2﹣2x+3x,
解得:x=﹣3(舍去)或,
即点P(,);
(3)是定值,理由:
由抛物线的表达式知,点D(﹣1,4),即MD=4,
设点Q(m,﹣m2﹣2m+3),
由点A、Q的坐标得,直线AQ的表达式为:y=(1﹣m)(x+3),
则点E(﹣1,2﹣2m),
同理可得:点F(﹣1,2m+6),
则ME+MF=2m+6+2﹣2m=8,
则2为定值.
14.【解答】解:(1)联立两个函数表达式得:x2﹣6x=x,
解得:x=7,即B(7,7);
由抛物线的表达式知,其对称轴为直线x=3,
当x=3时,y=x2﹣6x=9,即D(3,﹣9);
(2)如图,过点D作 DE⊥y轴于点E,
∴DE=3,OE=9,
∴,
∵,
∴∠DOE=∠PDO,
①当点P在线段OD的右侧时,DP∥y轴,如图,
∴P(3,0),
②当点P在线段OD左侧时,设直线DP与y轴交于点G,则△ODG 是等腰三角形,
∴OG=DG,设OG=t,则 DG=t,GE=9﹣t,
在Rt△DGE 中,t2=32+(9﹣t)2,
解得t=5,
∴G(0,﹣5),
∴直线DG的解析式为:
令y=0,则
解得 ,
综上,点P的坐标为(3,0)或 ;
(3)的值不变,理由如下:
由E(﹣a,0),F(6﹣a,0)知平移后的新的抛物线解析式为:y=(x+a)(x+a﹣6),
设直线EM的解析式为:y=k(x+a)
令(x+a)(x+a﹣6)=k(x+a),
解得:xE=﹣a,xM=k﹣a+6,
同理可得:xN=﹣k﹣a+6,
延长HF,过M,N分别作 MQ⊥FQ,NP⊥FP,垂足分别为Q,P,
∴QM=k﹣a+6﹣(6﹣a)=k,
PN=6﹣a﹣(﹣k﹣a+6)=k,
∴QM=PN,
由△MQH∽△NPH 得:.
15.【解答】解:(1)∵y=x2﹣2mx+m2﹣m+1=(x﹣m)2+(1﹣m),
∴M的坐标是(m,1﹣m);
(2)抛物线L与直线y=x有唯一公共点P,依题意得:
,
∴x2﹣2mx+m2﹣m+1=x,
∴x2﹣(2m+1)x+m2﹣m+1=0,
∴Δ=0,
∴(2m+1)2﹣4(m2﹣m+1)=0,
解得:,
∴M的坐标是,
当时,,
∴点P的坐标是,
∴;
(3)①∵抛物线的对称轴是y轴,
∴m=0,
∴抛物线的解析式为y=x2+1;
②设过点F的直线解析式为:y=kx+b,
由得:x2﹣kx+1﹣b=0,
∴xA+xB=k,xA xB=1﹣b,
记△AOB,△AOD,△BOE的面积分别为S1,S2,S3,
∵,
,
设,
整理得:(4﹣S) (1﹣b)b2=[S(1﹣b)+b2] k2,
∵S是定值,b是定值,
∴4﹣S=0,[S(1﹣b)+b2] k2=0,
∴S=4,4(1﹣b)+b2=0,
∴b=2,
∴F(0,2).
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练二次函数定值定点问题
1.综合与探究:
如图1,在平面直角坐标系中,抛物线y=ax2﹣2x+c与x轴交于点A(﹣3,0)和点C,与y轴交于点B(0,3),点P是抛物线上点A与点C之间的动点(不包括点A,点C).
(1)求抛物线的解析式;
(2)如图1,动点P在抛物线上,且在直线AB上方,求△ABP面积的最大值及此时点P的坐标;
(3)如图2,过原点O作直线l交抛物线于M、N两点,点M的横坐标为m,点N的横坐标为n.求证:mn是一个定值.
2.已知二次函数y=ax2+6的图象经过点P(4,2),直线AB与抛物线相交于A、B两点.
(1)求抛物线的解析式;
(2)如图1,若直线AB的解析式为y=kx﹣4k﹣3,且△PAB的面积为35,求k的值;
(3)如图2,若∠APB=90°,则直线AB必经过一个定点C,求点C的坐标.
3.已知如图1,平面直角坐标系中,O为原点,经过点(4,﹣8)的抛物线交x轴正半轴于点A(12,0),与直线l1:y=﹣x+p有两个交点B,C,它们的横坐标为m,n(m<n),且n﹣m=4.
(1)求抛物线C1的解析式;
(2)求△ABC的面积;
(3)如图2,将抛物线C1的顶点平移到原点O,得新抛物线L2,直线l2:y=k(x+2)+1(k<0)交抛物线L2于点D,E(点E横坐标小于﹣2),若l1与l2的交点为F,过点F作y轴平行线交抛物线L2于点G,试说明直线EG总经过定点,并求这个定点的坐标.
4.如图,二次函数y=x2+2x﹣3与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,抛物线的顶点为点D.
(1)直接写出点A,B,C的坐标;
(2)如图(1),连接AD,BD,点P为抛物线上一点,使,求点P的坐标;
(3)如图(2),过定点H(﹣2,﹣1)的直线与抛物线相交于M,N两点(点M在y轴左侧,点N在y轴右侧),过点M的直线y=﹣2x+b与抛物线交于点Q,求证:直线NQ必过定点.
5.已知抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0)两点,交y轴于点C(0,3).
(1)直接写出此抛物线的解析式为 ;
(2)如图1,在对称轴的右侧的抛物线上是否存在点P,使得△ACP为锐角三角形?若存在,求点P横坐标的取值范围;若不存在,请说明理由.
(3)如图2,E、F、G为抛物线上的点,且AF、EG交y轴于点(0,1),点P是直线EF和直线AG的交点,当点E在抛物线上运动(不与A、F重合)时,点P是否在定直线上运动?若是,求出此直线解析式;若不是,请说明理由.
6.在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)过A(6,0),B(0,2),D(4,2)三点,且与x轴交于另一点F.
(1)求抛物线的对称轴方程;
(2)如图1,点C为抛物线对称轴与x轴的交点,连接BC,直线BC交抛物线于另一点H,P为直线BC下方抛物线上的点,连接DH、HP,若∠DHB=∠BHP,求P点坐标;
(3)如图2,点M为第一象限内抛物线上一点,过点M的直线y=mx+n(n>0)与抛物线交于第四象限内一点N,连接FM、FN,分别交y轴于点D、E,且|OD| |OE|=4,求证:直线MN恒经过一定点,并求出定点坐标.
7.已知二次函数y=﹣x2+c的图象经过点A(﹣2,5),点P(x1,y1),Q(x2,y2)是此二次函数的图象上的两个动点.
(1)求此二次函数的表达式;
(2)如图1,此二次函数的图象与x轴的正半轴交于点B,点P在直线AB的上方,过点P作PC⊥x轴于点C,交AB于点D,连接AC,DQ,PQ.若x2=x1+3,求证:的值为定值;
(3)如图2,点P在第二象限,x2=﹣2x1,若点M在直线PQ上,且横坐标为x1﹣1,过点M作MN⊥x轴于点N,求线段MN长度的最大值.
8.如图1、抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C,顶点为D.
(1)求抛物线的解析式;
(2)P是x轴上一动点,将顶点D绕点P顺时针旋转90°刚好落在抛物线上的点E处,求点P的坐标;
(3)如图2,点G,H为x轴上方的抛物线上两点(点G在点H的左边),直线BG、BH与y轴分别交于S,T两点,若OS OT=9,试探究直线GH是否经过定点,若是,求定点坐标;若不是,请说明理由.
9.已知抛物线y=x2﹣2x﹣3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)直接写出A,B,C三点的坐标;
(2)如图1,点P为直线BC下方抛物线上一点,PD⊥BC于点D,求PD的最大值;
(3)如图2,M、N是抛物线上异于B,C的两个动点,若直线BN与直线CM的交点始终在直线y=2x﹣9上,求证:直线MN必经过一个定点,并求该定点坐标.
10.已知抛物线G1:ybx+c的图象与x轴交于点A(4,0),与y轴交于点C(0,2),点B(0,﹣2)为y轴上一点.
(1)求抛物线G1的解析式;
(2)如图1,点E是第一象限抛物线上一点,且∠ABE∠BAC,BE与x轴交于点D,求点E的横坐标;
(3)点P是G1上的一个动点,连接BP,取BP的中点P′,设点P′构成的曲线是G2,直线y=m与G1,G2的交点从左至右依次为P1,P2,P3,P4,则P3P4﹣P1P2是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
11.抛物线y=ax2+2ax+3(a<0)交x轴于A,B两点(A在B左边),交y轴于点C.
(1)直接写出抛物线的对称轴;
(2)已知AB=4.
①如图1,点D在第二象限抛物线上,BD交AC于点E.若BE=2DE,求点D的坐标;
②如图2,过点T(﹣1,t)(t>0)分别作直线l1:y=k1x+b1(k1>0)和直线l2:y=k2x+b2(k2<0),直线l1交抛物线于F,G两点,直线l2交抛物线于M,N两点.设线段FG,MN的中点分别为P,Q,若k1 k2=﹣2t,且k1+k2≠0,求证:直线PQ必经过一定点.
12.如图1,已知二次函数y=x2+bx+c的图象与x轴交于点A(﹣4,0)和点B,与y轴的负半轴交于点C(0,﹣4).
(1)求这个函数的解析式;
(2)点P是抛物线上的一点,当∠BCP=45°时,求点P的坐标;
(3)如图2,将直线AC向下平移与抛物线交于M、N两点,直线AM、CN交于Q点,请问点Q的横坐标是否为定值,并说明理由.
13.如图1,已知y=ax2﹣bx﹣3a过点A(﹣3,0)和点C(0,3).
(1)求此抛物线的解析式;
(2)在第一象限抛物线上是否存在一点P,使得∠PAB+∠BCO=45°,请求出P点的坐标;
(3)如图2所示,对称轴交x轴于点M,顶点为点D,在第二象限抛物线上有一动点Q,直线AQ,BQ与对称轴分别相交于点E、F,当点Q运动时,试探究的值是否为一个定值,若是,求出该定值;若不是,说明理由.
14.抛物线y=x2﹣6x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
(1)直接写出点B和点D的坐标;
(2)如图1,连接OD,P为x轴上的动点,当时,求点P的坐标;
(3)如图2,将抛物线y=x2﹣6x沿x轴水平向左平移a个单位(a>0),新的抛物线与x轴交于E,F两点.点M为第一象限抛物线上的一个动点,连接EM,作EM关于x轴对称的直线EN交抛物线于点N,连接MN,过F点作y轴的平行线HF交MN于点H,当M点运动时,的值是否变化?若不变,求出它的值;若变化,说明理由.
15.已知抛物线L:y=x2﹣2mx+m2﹣m+1(m为常数),顶点为M.
(1)求M的坐标(用含m的式子表示);
(2)若抛物线L与直线y=x有唯一公共点P,求PM的长.
(3)如图,若抛物线L的对称轴为y轴,顶点为C,过y轴正半轴上一定点F(点F在点C上方)的任意直线交抛物线L于点A,B,分别过点A,B作x轴的垂线,垂足分别为点D,E,连OA,OB.
①直接写出抛物线L的解析式;
②若记△AOB,△AOD,△BOE的面积分别为S1,S2,S3,当为定值时,求定点F坐标.
参考答案
1.【解答】(1)解:在平面直角坐标系中,抛物线y=ax2﹣2x+c与x轴交于点A(﹣3,0)和点C,与y轴交于点B(0,3),把点A(﹣3,0)和点B(0,3)的坐标代入得:
,
解得:,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)解:如下图所示,过点P作PH∥y轴,交AB于点H,
设直线AB的解析式为y=kx+b,把点A和点B的坐标代入得:
,
解得:,
∴直线AB的解析式为y=x+3,
点P是抛物线上点A与点C之间的动点(不包括点A,点C).设点P的横坐标为x,则点P的纵坐标为﹣x2﹣2x+3,
∴点H的横坐标为x,点H的纵坐标为x+3,
∴PH=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x,
∵S△APB=S△APH+S△BPH,
整理得:S△APBx,
∴可知当时,△APB的面积有最大值,最大值是,
当时,,
此时点P的坐标为;
(3)证明:设直线MN的解析式为y=hx,
解方程组,
可得:﹣x2﹣2x+3=hx,
整理得:x2+(2+h)x﹣3=0,
一元二次方程x2+(2+h)x﹣3=0中,
Δ=b2﹣4ac=(2+h)2+12>0,
∴一元二次方程x2+(2+h)x﹣3=0有两个不相等的实数根,
这两个不相等的实数根分别为m、n,
则有,
∴mn是一个定值.
2.【解答】解:(1)∵二次函数y=ax2+6的图象经过点P(4,2),
∴16a+6=2,
解得a,
∴抛物线的解析式为:yx2+6;
(2)已知直线AB的解析式为y=kx﹣4k﹣3,
令x=4,则y=﹣3,
∴直线AB过定点D(4,﹣3),
∵P(4,2),
∴PD∥y轴,PD=5,
∴S△ABP PD |xB﹣xA|=35,
∴|xB﹣xA|=14,
令x2+6=kx﹣4k﹣3,整理得x2+4kx﹣16k﹣36=0,
∴xB+xA=﹣4k,xB xA=﹣16k﹣36,
∴|xB﹣xA|2=(xB+xA)2﹣4xB xA=142,
整理得16k2+64k﹣52=0,
解得k=﹣2或k=﹣2;
(3)设A(m,m2+6),B(n,n2+6),如图2,过点P作直线PN∥x轴,分别过A、B两点作PN的垂线,垂足分别为N、M,
∵∠APB=90°,△PAN∽△BPM,
∴AN:PM=PN:BM,
∴,即,
∴(m+4)(n+4)=﹣16,
∴mn+4(m+n)+32=0①,
联立方程组,
∴x2+tx+b﹣6=0,
∴m+n=﹣4t,mn=4b﹣24②,
将②代入①,得化简,得
b=4t﹣2,
∴直线AB的解析式为y=tx+4t﹣2,即y=t(x+4)﹣2,
∴直线AB经过定点C(﹣4,﹣2).
3.【解答】解:(1)∵抛物线经过点(4,﹣8)和点(12,0),
∴,
解得:,
∴抛物线C1的解析式为yx2﹣3x;
(2)∵抛物线与直线l1:y=﹣x+p有两个交点B,C,它们的横坐标为m,n(m<n),
联立得:x2﹣3x=﹣x+p,
整理得:x2﹣8x﹣4p=0,
∴m+n=8,
又∵n﹣m=4,
∴m=2,n=6,
∴B(2,﹣5),C(6,﹣9),
把B(2,﹣5)代入y=﹣x+p,得:﹣5=﹣2+p,
解得:p=﹣3,
∴直线l1:y=﹣x﹣3,
当y=0时,﹣x﹣3=0,
解得:x=﹣3,
∴直线l1:y=﹣x﹣3与x轴交于点M(﹣3,0),如图,
∵A(12,0),B(2,﹣5),C(6,﹣9),
∴AM=12﹣(﹣3)=15,
∴S△ABC=S△ACM﹣S△ABMAM |yC|AM |yB|15×915×5=30;
(3)∵抛物线C1:yx2﹣3x(x﹣6)2﹣9,顶点坐标为(6,﹣9),将抛物线C1的顶点平移到原点O,得新抛物线L2,
∴新抛物线L2:yx2,
联立直线l2与新抛物线的解析式,得x2=k(x+2)+1,
解得:xD=﹣2,xE=4k+2,
联立直线l1与l2的解析式,得:k(x+2)+1=﹣x﹣3,
解得:x,
∵FG∥y轴,交抛物线L2于点G,
∴G(,),
设直线EG的解析式为:y=k′x+b′,则x2=k′x+b′,
整理得:x2﹣4k′x﹣4b′=0,
∴xE+xG=4k′,xE xG=﹣4b′,
∴k′(xE+xG)(4k+2),
b′xE xG(4k+2)(),
∴直线EG的解析式为yx,
当x=﹣2时,y(﹣2)3,
∴直线EG经过定点(﹣2,3).
4.【解答】(1)对于y=x2+2x﹣3,当x=0时,y=﹣3,令y=0,则x=1或﹣3,
则点A、B、C的坐标分别为:(﹣3,0)、(1,0)、(0,﹣3);
(2)由抛物线的表达式知,点D(﹣1,﹣4),
过点D作DE∥y轴交x轴于点E,
由函数的对称性值,∠ADE∠ADB,
由点A、D的坐标得,tan∠ADEtan∠PAO,
则直线PA的表达式为:y=±(x+3),
联立上式和抛物线的表达式得:x2+2x﹣3±(x+3),
解得:x=﹣3(舍去)或或,
即点P(,)或(,);
(3)证明:设M(p,p2+2p﹣3),N(q,q2+2q﹣3),
由点M、N的坐标得,直线MN解析式为y=(p+q+2)x﹣pq+3,
∵直线MN过定点(﹣2,﹣1),
∴﹣2(p+q+2)﹣pq﹣3=﹣1,
∴pq=﹣2p﹣2q+6,
∵直线y=﹣2x+b过M(p,p2+2p﹣3),
∴P2+2P﹣3=﹣2P+b,
∴b=P2+4q﹣3,
∴y=﹣2x﹣P2+4P﹣3,
由﹣2x﹣P2+4P﹣3=﹣x2+2x+3得:x=P或x=﹣P﹣4,
∴G(﹣P﹣4,P2+6P+5),
由N、Q的坐标得,直线NQ解析式为y=(﹣p﹣4+q+2)x﹣(﹣p﹣4)q﹣3,
∵pq=﹣2p﹣2q+6,
则y=(﹣p+q﹣2)x﹣2p+2q﹣9,
当x=﹣2时,y=﹣2(﹣p+q﹣2)﹣2p+2q﹣9=﹣5,
∴直线MG必过定点(﹣2,﹣5).
5.【解答】解:(1)由题意可设交点式y=a(x+1)(x﹣3),代入(0,3),得3=a×1×(﹣3),解得a=﹣1,
∴此抛物线的解析式为y=﹣x2+2x+3,
故答案为:y=﹣x2+2x+3;
(2)存在点P,使得△ACP为锐角三角形,理由如下:
作P'C⊥AC于点C交抛物线于点P',过点C作DE∥x轴,P'E⊥DE于点E,AD⊥DE于点D,如图1所示,
设P'(m,﹣m2+2m+3),
∵∠DCA+∠ECP'=90°,∠DCA+∠DAC=90°,
∴∠ECP'=∠DAC,
从而tan∠ECP'=tan∠DAC,即,
∴,解得m或0(舍去);
作P''A⊥CA于点A交抛物线于点P'',作P''F⊥DA的延长线于点F,
设P''(m,﹣m2+2m+3),
同理可证tan∠AP''F=tan∠DAC,即,
∴,解得m,
故点P横坐标的取值范围为.
(3)解法一(点参法):
∵A(﹣1,0),H(0,1),
∴由待定系数法可得直线AG的解析式为y=x+1,
与抛物线y=﹣x2+2x+3联立可得x+1=﹣x2+2x+3,解得xF=2,
故F(2,3).
设E(m,﹣m2+2m+3),G(n,﹣n2+2n+3),A(﹣1,0),
则由待定系数法可得直线EG的解析式为y=(2﹣m﹣n)x+3+mn,
∵直线EG过点H(0,1),
∴1=3+mn,mn=﹣2,
同理得直线AG的解析式为y=(3﹣n)x+3﹣n,
直线EF的解析式为y=﹣mx+2m+3,
联立直线AG与直线EF得﹣mx+2m+3=(3﹣n)x+3﹣n,
得x,即xP,
∴yP=(3﹣n)(x+1)
=(3﹣n)
=5+2xP.
故点P在直线y=2x+5上.
解法二(线参法):
∵直线EF过点F(2,3),直线AG过点A(﹣1,0),
故设直线EF解析式为y=k(x﹣2)+3,直线AG解析式为y=m(x+1),
联立直线EF和抛物线y=﹣x2+2x+3,可得x2+(k﹣2)x﹣2k=0,由韦达定理知xE+2=2﹣k,
故xE=﹣k,则E(﹣k,﹣k2﹣2k+3),
联立直线AG与抛物线y=﹣x2+2x+3,可得x2+(m﹣2)x+m﹣3=0,由韦达定理知xG+(﹣1)=2﹣m,
故xG=3﹣m,则G(3﹣m,﹣m2+4m),
由待定系数法可得直线EG的解析式为y=(k+m﹣1)x+k(m﹣3)+3,
又∵直线EG过点H(0,1),
则k(m﹣3)+3=1,即km=3k﹣2,
联立直线EF与直线AG,可得(k﹣m)x=m+2k﹣3,解得x,
即xP,
故yP=m(x+1)
=m
=5+2xP,
故点P在直线y=2x+5上.
6.【解答】解:(1)∵抛物线y=ax2+bx+c过B(0,2),D(4,2),
∴抛物线的对称轴方程为直线x.
(2)∵对称轴为直线x,
∴b=﹣4a,
∴抛物线y=ax2﹣4ax+2,代入点A(6,0),得6a=﹣1,
解得a,
∴抛物线解析式为yx2x+2.
∵点C为抛物线对称轴与x轴的交点,
∴C(2,0),
又∵B(0,2),
由待定系数法可知直线BC的解析式为y=﹣x+2,
联立y=﹣x+2与yx2x+2,得x2﹣10x=0,
解得x=10或0(舍去),
即H(10,﹣8).
如图1所示,设PH交y轴于点F,
∵OB=OC=2,
∴∠OBC=∠OCB=45°,
∵BD∥OC,
∴∠DBC=∠OCB=45°,
当∠DHB=∠BHP时,
在△BFH和△BDH中,
∵,
∴△BFH≌△BDH(ASA),
∴BF=BD=4,
故F(0,﹣2),
则由待定系数法可得直线HF的解析式为y,
联立直线HF解析式与抛物线解析式可得5x2﹣38x﹣120=0,
解得x=10或,
故P点坐标为(,).
(3)证明:如图2所示,设M(m,),N(n,),
故由待定系数法可得直线MN的解析式为y=[(m+n)]x2.
∵A(6,0),再由抛物线对称性可知F(﹣2,0),
同理可得直线FM的解析式为y=[(m﹣2)]x+2,
则OD2,
同理可得直线FN的解析式为y=[(n﹣2)]x+2,
则OE,
∵|OD| |OE|=4,即(2)()=4,化简整理可得(6﹣m)(n﹣6)=36,
进而可得mn=6(m+n)﹣72①,
把①式代入直线MN的解析式中,得:
y=[(m+n)]x2
=[(m+n)]x
,
令,解得x=6,此时y=﹣6,
故直线MN恒过定点(6,﹣6).
7.【解答】(1)解:将点A的坐标代入抛物线表达式得:5=﹣4+c,
则c=9,
即抛物线的表达式为:y=﹣x2+9;
(2)证明:令y=﹣x2+9,则x=±3,则点B(3,0),
由点A、B的坐标得,直线AB的表达式为:y=﹣x+3,
设点P、Q、D的表达式分别为:(x1,9)、(x2,9)、(x1,﹣x1+3),
则S△PDQPD×(xQ﹣xP)(9+x1﹣3)(x2﹣x1)(x1+6),
同理可得:S△ADCCD×(xD﹣xA)(x1+6),
则3为定值;
(3)解:点P、Q的坐标分别为:(x1,9)、(﹣2x1,﹣49),
由点P、Q的坐标得,直线PQ的表达式为:y=x1(x﹣x1)9=xx1﹣29,
则MN=yM=(x1﹣1)x1﹣29=﹣(x1)2,
故MN的最大值为:.
8.【解答】解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0)两点,
∴,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)设P(t,0),过点E作EF⊥x轴于点F,设抛物线的对称轴交x轴于点K,如图1,
则∠DKP=∠PFE=90°,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4),K(1,0),
∴PK=1﹣t,DK=4,
设E(e,﹣e2+2e+3),则F(e,0),
∴EF=﹣(﹣e2+2e+3)=e2﹣2e﹣3,PF=e﹣t,
由旋转得:PE=PD,∠DPE=90°,
∴∠DPK+∠EPF=90°,
∵∠DPK+∠PDK=90°,
∴∠EPF=∠PDK,
∴△PEF≌△DPK(AAS),
∴EF=PK,PF=DK,
∴,
解得:,,
∴点P的坐标为(,0)或(,0);
(3)直线GH经过定点(﹣1,1).理由如下:
设G(m,﹣m2+2m+3),H(n,﹣n2+2n+3),
设直线GH的解析式为y=kx+d,则,
解得:,
∴直线GH的解析式为y=(﹣m﹣n+2)x+mn+3,
同理可得:直线BG的解析式为y=﹣(m+1)(x﹣3),
直线BH的解析式为y=﹣(n+1)(x﹣3),
令x=0,则yS=3(m+1),yT=3(n+1),
∴OS=3(m+1),OT=3(n+1),
∵OS OT=9,
∴3(m+1)×3(n+1)=9,
∴m+n=﹣mn,
代入直线GH的解析式得y=(mn+2)x+mn+3,
∵当x=﹣1时,y=1,
∴直线GH经过定点(﹣1,1).
9.【解答】(1)解:对于y=x2﹣2x﹣3,令y=0,则0=x2﹣2x﹣3,
∴x1=﹣1,x2=3,
∴点A(﹣1,0),点B(3,0),
令x=0,则y=﹣3,
∴点C(0,﹣3);
(2)解:过点P作PE⊥x轴于E,交BC于点F,如图1:
设直线BC的解析式为y=kx+b,
将点B(3,0),C(0,﹣3)代入y=kx+b得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
设P(x,x2﹣2x﹣3),则F(x,x﹣3),
∴PF=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∵PE⊥x轴,
∴PE∥y轴,
∴∠PFD=∠BCO,
∵∠PDF=∠BOC=90°,
∴△PDF∽△BCO,
∴,
∵B(3,0),C(0,﹣3),
∴OB=3,OC=3,
∴BC=3,
∴,
∴PDx2x,
∴当x时,PD最大为;
(3)证明:如图2,设点M(xM,yM),N(xN,yN),
直线MN:y=k′x+b′,直线CM:y=k1x+b1,直线BN:y=k2x+b2,
将点C(0,﹣3)代入直线CM的解析式得:b1=﹣3,
将点B(3,0)代入直线BN的解析式得:b2=﹣3k2,
联立直线MN与抛物线的解析式得:,
整理得:x2﹣(k′+2)x﹣b′﹣3=0,
则xM+xN=k′+2,xM xN=﹣b′﹣3,
同理:xM+xC=k1+2,xN+xB=k2+2,
∵xC=0,xB=3,
∴xM=k1+2,xN=k2﹣1,
∴k′=xM+xN﹣2=k1+2+k2﹣1﹣2=k1+k2﹣1,
b′=﹣xM xN﹣3=﹣(k1+2)(k2﹣1)﹣3=﹣k1k2﹣2k2+k1+2﹣3=﹣k1k2﹣2k2+k1﹣1,
联立直线CM与直线BN的解析式得:,
解得:,
∵直线BN与直线CM的交点始终在直线y=2x﹣9上,
∴29,
化简得:k1k2=3k1﹣2,
∴b′=﹣k1k2﹣2k2+k1﹣1=﹣3k1+2﹣2k2+k1﹣1=﹣2k1﹣2k2+1=﹣2(k1+k2)+1=﹣2(k′+1)+1=﹣2k′﹣1,
∴直线MN:y=k′x﹣2k′﹣1=k′(x﹣2)﹣1,
∴不论k′为何值,均有x=2时,y=﹣1,
即:直线MN恒过定点P(2,﹣1).
10.【解答】解:(1)将点A(4,0),C(0,2)代入抛物线G1,
得到,
解得,
∴抛物线G1的解析式为,
(2)∵A(4,0),B(0,﹣2),C(0,2),
∴OA=4,OB=OC=2,
又∵OA⊥BC,
∴AC=AB,
∴OA平分∠BAC,
∵,
∴∠ABE=∠OAB,
∴BD=AD,
设OD=m,则AD=BD=4﹣m,
在Rt△OBD中,OD2+OB2=BD2,
∴m2+22=(4﹣m)2,
解得,,
∴,
设直线BD解析式为y=kx﹣2,代入点D,则,
解得,
∴直线BD解析式为,
联立抛物线G1与直线BD,
∴,
得,x2=﹣6(舍去),
∴点E的横坐标为;
(3)P3P4﹣P1P2为定值,理由如下:
设点P′(x,y),作P′M⊥y轴于M,作PN⊥y轴于N,则P′M∥PN,M(0,y),如图2,
又∵P′为PB中点,
∴P′M为△PBM中位线,
∴PN=2P′M,M为BN中点,
∴xP=2x,yP﹣y=y﹣(﹣2),
∴yP=2y+2,
∴P(2x,2y+2),
将点P代入抛物线G1,
∴,
化简得,
设P1,P2,P3,P4的横坐标分别为x1,x2,x3,x4,
则P3P4﹣P1P2=(x4﹣x3)﹣(x2﹣x1)=(x4+x1)﹣(x2+x3),
由得x4+x1=2,
由得x2+x3=1,
∴P3P4﹣P1P2=2﹣1=1定值.
11.【解答】解:(1)∵y=ax2+2ax+3
∴抛物线的对称轴为:直线 x1;
(2)①过点D作DP∥y轴交AC于点P,过点B作BQ∥y轴交AC的延长线于点Q.
∴DP∥BQ,
∴△DPE∽△BQE,
∴,
∵BE=2DE,
∴BQ=2DP,
∵AB=4,抛物线的对称轴为直线 x=﹣1,
∴A(﹣3,0),B(1,0),C(0,3),
∴a=﹣1,AC:y=x+3,
∴Q(1,4),
∴BQ=4,DP=2,
设D(t,﹣t2﹣2t+3),则P(t,﹣t2﹣2t+1),
∵直线y=x+3经过点P,
∴t+3=﹣t2﹣2t+1,
解得:t1=﹣1,t2=﹣2,
∴D点的坐标为(﹣1,4)或 (﹣2,3);
②联立得x2+(k1+2)x+b1﹣3=0,
∴xF+xG=﹣k1﹣2,
∴,
联立得x2+(k2+2)x+b2﹣3=0,
同理可得:,
∵l1,l2经过点T(﹣1,t),
∴﹣k1+b1=t,﹣k2+b2=t,
即:b1=k1+t,b2=k2+t,
∴l1:y=k1x+k1+t+t,l2:y=k2x+k2+t,
∴,Q(),
∵k1 k2=﹣2t,
设直线PQ的解析式为y=kx+b,则,
解得:,
∴直线PQ的解析式为y=(k1+k2)x+(k1+k2),
∴直线PQ恒过定点(﹣1,0).
12.【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=x2+3x﹣4①;
(2)由抛物线的表达式知,点B(1,0),
则tan∠OBC=4,
设直线CP交x轴于点H,过点H作HN⊥BC于点N,
在△BCH中,BC,
设HN=4x=CN,则HN=x,
则BHx,BC=BN+CN=5x,
则x,则BHx,
则点H(,0),
由点C、H得,直线CH的表达式为:yx﹣4②,
联立①②得:x2+3x﹣4x﹣4,
解得:x=0(舍去)或,
则点P(,);
(3)由点A、C的坐标得,直线AC的表达式为:y=﹣x﹣3,
则设直线MN的表达式为:y=﹣x+t③,
联立①③并整理得:x2+4x﹣(t+4)=0,
则m+n=﹣4,
设点M、N的坐标分别为:(m,m2+3m﹣4)、(n,n2+3n﹣4),
由点A、M得,直线AM的表达式为:y=(m﹣1)(x+4),
同理可得,直线CN的表达式为:y=(n+3)x﹣4,
联立上述两式得:(m﹣1)(x+4)=(n+3)x﹣4,
解得:x2.
即Q的横坐标是否为定值,为﹣2.
13.【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2﹣2x+3;
(2)设直线AP交y轴于点H,过点H作HN⊥AC于点N,
在Rt△OCB中,tan∠OCB,
由OC=OA=3知,∠ACH=45°=∠CAO,
∵∠HAO+∠CAO=45°,∠PAB+∠BCO=45°,
∴∠CAH=∠OCB,则tan∠CAH=tan∠OCB,
在△ACH中,∠ACH=45°,tan∠CAH=tan∠OCB,AC=3,
故设NH=x=CN,则AH=3x,CHx,
则AC=4x=3,则x,
则CHx,则点H(0,),
由点A、H的坐标得,直线AH的表达式为:yx,
联立上式和抛物线的表达式得:﹣x2﹣2x+3x,
解得:x=﹣3(舍去)或,
即点P(,);
(3)是定值,理由:
由抛物线的表达式知,点D(﹣1,4),即MD=4,
设点Q(m,﹣m2﹣2m+3),
由点A、Q的坐标得,直线AQ的表达式为:y=(1﹣m)(x+3),
则点E(﹣1,2﹣2m),
同理可得:点F(﹣1,2m+6),
则ME+MF=2m+6+2﹣2m=8,
则2为定值.
14.【解答】解:(1)联立两个函数表达式得:x2﹣6x=x,
解得:x=7,即B(7,7);
由抛物线的表达式知,其对称轴为直线x=3,
当x=3时,y=x2﹣6x=9,即D(3,﹣9);
(2)如图,过点D作 DE⊥y轴于点E,
∴DE=3,OE=9,
∴,
∵,
∴∠DOE=∠PDO,
①当点P在线段OD的右侧时,DP∥y轴,如图,
∴P(3,0),
②当点P在线段OD左侧时,设直线DP与y轴交于点G,则△ODG 是等腰三角形,
∴OG=DG,设OG=t,则 DG=t,GE=9﹣t,
在Rt△DGE 中,t2=32+(9﹣t)2,
解得t=5,
∴G(0,﹣5),
∴直线DG的解析式为:
令y=0,则
解得 ,
综上,点P的坐标为(3,0)或 ;
(3)的值不变,理由如下:
由E(﹣a,0),F(6﹣a,0)知平移后的新的抛物线解析式为:y=(x+a)(x+a﹣6),
设直线EM的解析式为:y=k(x+a)
令(x+a)(x+a﹣6)=k(x+a),
解得:xE=﹣a,xM=k﹣a+6,
同理可得:xN=﹣k﹣a+6,
延长HF,过M,N分别作 MQ⊥FQ,NP⊥FP,垂足分别为Q,P,
∴QM=k﹣a+6﹣(6﹣a)=k,
PN=6﹣a﹣(﹣k﹣a+6)=k,
∴QM=PN,
由△MQH∽△NPH 得:.
15.【解答】解:(1)∵y=x2﹣2mx+m2﹣m+1=(x﹣m)2+(1﹣m),
∴M的坐标是(m,1﹣m);
(2)抛物线L与直线y=x有唯一公共点P,依题意得:
,
∴x2﹣2mx+m2﹣m+1=x,
∴x2﹣(2m+1)x+m2﹣m+1=0,
∴Δ=0,
∴(2m+1)2﹣4(m2﹣m+1)=0,
解得:,
∴M的坐标是,
当时,,
∴点P的坐标是,
∴;
(3)①∵抛物线的对称轴是y轴,
∴m=0,
∴抛物线的解析式为y=x2+1;
②设过点F的直线解析式为:y=kx+b,
由得:x2﹣kx+1﹣b=0,
∴xA+xB=k,xA xB=1﹣b,
记△AOB,△AOD,△BOE的面积分别为S1,S2,S3,
∵,
,
设,
整理得:(4﹣S) (1﹣b)b2=[S(1﹣b)+b2] k2,
∵S是定值,b是定值,
∴4﹣S=0,[S(1﹣b)+b2] k2=0,
∴S=4,4(1﹣b)+b2=0,
∴b=2,
∴F(0,2).
21世纪教育网(www.21cnjy.com)
同课章节目录
