第二十四章 圆 学情评估卷(含答案)人教版数学九年级上册
文档属性
| 名称 | 第二十四章 圆 学情评估卷(含答案)人教版数学九年级上册 | 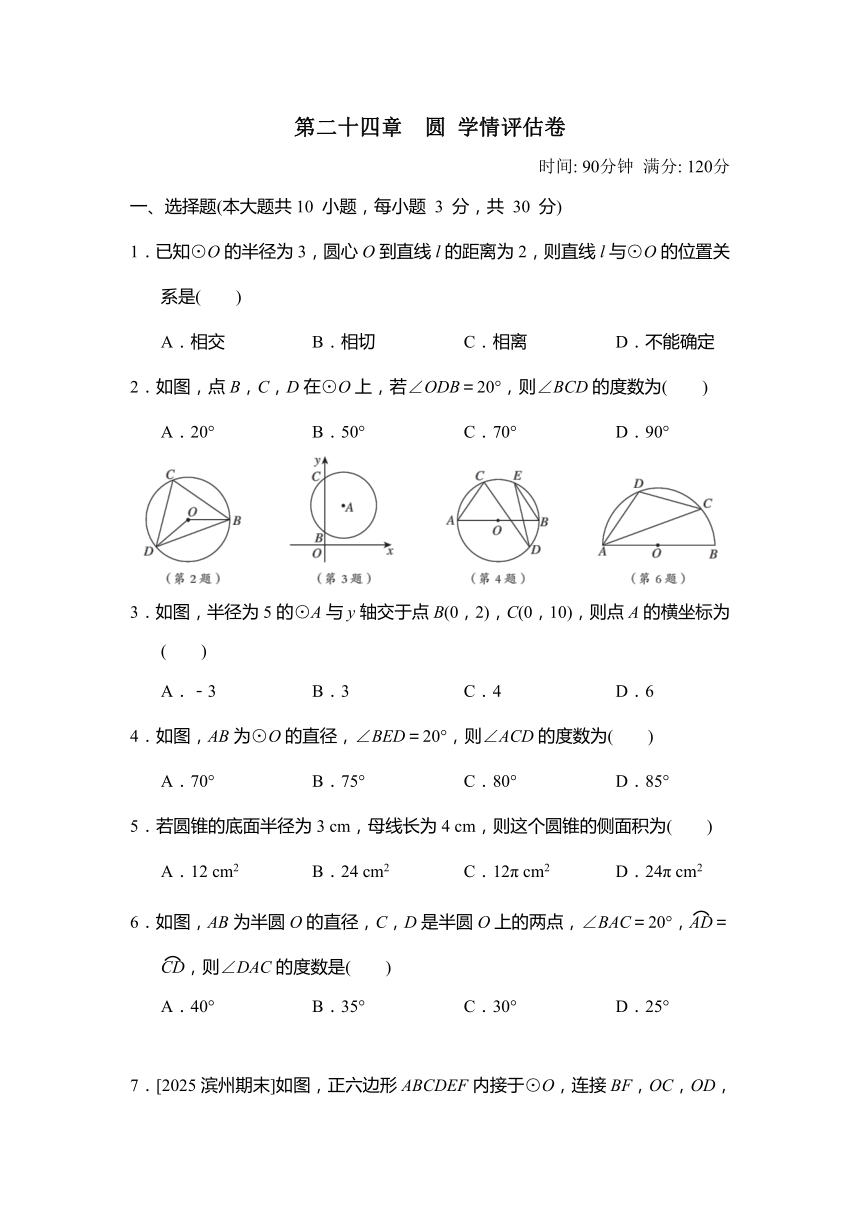 | |
| 格式 | doc | ||
| 文件大小 | 668.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 07:51:49 | ||
图片预览





文档简介
第二十四章 圆 学情评估卷
时间: 90分钟 满分: 120分
一、选择题(本大题共10 小题,每小题 3 分,共 30 分)
1.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.如图,点B,C,D在⊙O上,若∠ODB=20°,则∠BCD的度数为( )
A.20° B.50° C.70° D.90°
3.如图,半径为5的⊙A与y轴交于点B(0,2),C(0,10),则点A的横坐标为( )
A.-3 B.3 C.4 D.6
4.如图,AB为⊙O的直径,∠BED=20°,则∠ACD的度数为( )
A.70° B.75° C.80° D.85°
5.若圆锥的底面半径为3 cm,母线长为4 cm,则这个圆锥的侧面积为( )
A.12 cm2 B.24 cm2 C.12π cm2 D.24π cm2
6.如图,AB为半圆O的直径,C,D是半圆O上的两点,∠BAC=20°,=,则∠DAC的度数是( )
A.40° B.35° C.30° D.25°
7.[2025滨州期末]如图,正六边形ABCDEF内接于⊙O,连接BF,OC,OD,则∠BFE-∠COD=( )
A.90° B.60° C.45° D.30°
8.如图,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,连接OE,OF,若∠C=90°,AC=3,BC=4,则阴影部分的面积为( )
A.2-π B.4-π C.4-π D.1-π
9.如图,在平面直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙A与直线l:y=x只有一个公共点时,点A的坐标为( )
A.(-12,0) B.(-13,0) C.(±12,0) D.(±13,0)
10.[2025金华月考]如图,直线y=-x+6与坐标轴交于A,B两点,点C为坐标平面内一点,BC=2,点M为线段AC的中点,连接OM,则线段OM长度的最小值是( )
A.3+1 B.3-1 C.2 D.3
二、填空题(本大题共6 小题,每小题 4 分,共 24 分)
11.如图,AB为⊙O的直径,AB=1 cm,BC= cm,当AC=________cm时,直线AC与⊙O相切.
12.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=8,则⊙O的半径OA等于______.
13.如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应的刻度值为64°,则∠BCD的度数为________.
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图,点M表示筒车的一个盛水桶,当筒车工作时,盛水桶的运行路径是以轴心O(O在水面上方)为圆心的圆,且⊙O的半径(OA)为5米.若筒车工作时,盛水桶在水面以下的最大深度为2米,则这个圆被水面截得的弦AB的长为________米.
15.如图,四边形ABCD是⊙O的内接四边形,点O在四边形ABCD内部,过点C作⊙O的切线交AB的延长线于点P,连接OA,OB.若∠AOB=140°,∠BCP=35°,则∠ADC的度数为________.
16.如图,三条笔直的小路a,b,c相交围成一个三角形公园ABC,在△ABC的内心I处修建了一个凉亭,过凉亭的小路d∥c,并分别与△ABC的两边AB,AC相交于点D,E,DE=150 m,小路c与d之间相距60 m,如果从凉亭分别向小路a,b,c修建一条石板路,那么这三条石板路的长度之和最小为________m,若游客从B处出发,沿B→D→I→E→C的路线,到达C处,那么所走的这段路程长为________m.
三、解答题(本大题共7小题,共66分,各小题都必须写出解答过程)
17.(8分)如图,已知⊙O的两条弦AB,CD相交于点M,且AB=CD,连接AD.求证:AM=DM.
18.(8分)如图,在△ABC中,AC=AB,以AB为直径的⊙O分别交AC,BC于点D,E,连接OD.
(1)求证:CE=BE;
(2)若∠C=70°,求∠BOD的度数.
19.(8分)如图,在平面直角坐标系中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
(1)若△ABC的外接圆的圆心为M,则点M的坐标为________,⊙M的半径为________;
(2)△ABC的外接圆与x轴的另一个交点的坐标是________;
(3)求⊙M中的长.
20.(10分)如图①,已知圆锥的母线长l=16 cm,若以圆锥的顶点为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角为270°.
(1)求圆锥的底面半径r;
(2)求圆锥的全面积.
21.(10分)[2024南通中考]如图,在△ABC中,AB=3,AC=4,BC=5,⊙A与BC相切于点D.
(1)求图中阴影部分的面积;
(2)设⊙A上有一动点P,连接CP,BP.当CP的长最大时,求BP的长.
22.(10分)[2024自贡中考]在Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F.
(1)图①中三组相等的线段分别是CE=CF,AF=________,BD=________;若AC=3,BC=4,则⊙O半径长为________.
(2)如图②,延长AC到点M,使AM=AB,过点M作MN⊥AB于点N.求证:MN是⊙O的切线.
23.(12分)如图①,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E,F都在直线l上,且AB=7,EF=10,BC>5.点B以每秒1个单位长度的速度从点E处出发,沿射线EF的方向运动,矩形ABCD随之运动,运动时间为t秒.
(1)如图②,当t=2.5时,求半圆O在矩形ABCD内的弧的长度;
(2)在点B运动的过程中,当AD,BC都与半圆O相交时,设AD与半圆O交于点G,BC与半圆O交于点H.连接OG,OH,若∠GOH为直角,求此时t 的值.
答案
一、1.A 2.C 3.B 4.A 5.C 6.B 7.D 8.D 9.D 10.B
二、11.1 12.4 13.58° 14.8
15.105° 16.180;300
三、17.证明:∵AB=CD,∴=,
即+=+.
∴=.∴∠D=∠A.
∴AM=DM.
18.(1)证明:连接AE,
∵AB是⊙O的直径,∴∠AEB=90°.
∴AE⊥BC.又∵AB=AC,
∴E是BC的中点,∴CE=BE.
(2)解:∵AB=AC,
∴∠B=∠C=70°,
∴∠BAC=180°-∠B-∠C=40°.
∵∠BAC=∠BOD,∴∠BOD=80°.
19.解:(1)(5,5); (2)(7,0)
(3)连接MC,MA.
∵A(0,7),C(3,0),M(5,5),
∴AC==,MC=MA=.∴MC2+MA2=AC2.
∴△MAC是直角三角形,
且∠AMC=90°.
∴的长为=.
20.解:(1)由题意得3×2πr=,∴r=4 cm.
(2)圆锥的全面积为π×42+×2×4π×16=80π(cm2).
21.解:(1)如图,连接AD,
∵AB=3,AC=4,BC=5,
∴AB2+AC2=32+42=25=52=BC2,∴∠BAC=90°.
∵BC与⊙A相切于点D,∴AD⊥BC.
∴S△ABC=AD·BC=AC·AB,
∴AD===,
∴S阴影=S△ABC-S扇形=×3×4-=6-π.
(2)如图,当点P在CA的延长线上时,CP的长最大,由(1)知∠BAC=∠PAB=90°,AP=AD=,
∴PB==.
22.(1)AD;BE;1
(2)证明:如图,连接OD,OE,OF,OA,OM,ON,OC,OB,作OG⊥MN于点G,
设⊙O半径为r,
∵MN⊥AB,
∴∠ACB=∠ANM=90°.又∵∠CAB=∠NAM,AB=AM,
∴△CAB≌△NAM,
∴S△CAB=S△NAM,AN=AC,MN=BC.
∵⊙O是△ABC的内切圆,切点分别为D,E,F,∴OD=OE=OF=r,
∴S△ABC=(AC+BC+AB)·r,同理S△AMN=(AN+AM)·r+MN·OG,
∴(AC+BC+AB)·r=(AN+AM)·r+MN·OG,
∴OG=r,即OG为⊙O的半径.
又∵OG⊥MN,∴MN是⊙O的切线.
23.解:(1)设BC与半圆O交于点M,连接ME,MO.当t=2.5时,BE=2.5.
∵EF=10,∴OE=EF=5.
∴OB=2.5.∴EB=OB.
在矩形ABCD中,∠ABC=90°,
∴ME=MO.
又∵MO=EO,∴ME=EO=MO=5.
∴△MOE是等边三角形.∴∠EOM=60°.∴的长度为=,即半圆O在矩形ABCD内的弧的长度为.
(2)∵∠GOH=90°,
∴∠AOG+∠BOH=90°.
∵∠AGO+∠AOG=90°,
∴∠AGO=∠BOH.
在△AGO和△BOH中,
∴△AGO≌△BOH.∴OB=AG=t-5.∵AB=7,∴AE=t-7,
∴AO=5-(t-7)=12-t.
在Rt△AGO中,AG2+AO2=OG2,
∴(t-5)2+(12-t)2=52,
解得t1=8,t2=9,即t的值为8或9.
时间: 90分钟 满分: 120分
一、选择题(本大题共10 小题,每小题 3 分,共 30 分)
1.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.如图,点B,C,D在⊙O上,若∠ODB=20°,则∠BCD的度数为( )
A.20° B.50° C.70° D.90°
3.如图,半径为5的⊙A与y轴交于点B(0,2),C(0,10),则点A的横坐标为( )
A.-3 B.3 C.4 D.6
4.如图,AB为⊙O的直径,∠BED=20°,则∠ACD的度数为( )
A.70° B.75° C.80° D.85°
5.若圆锥的底面半径为3 cm,母线长为4 cm,则这个圆锥的侧面积为( )
A.12 cm2 B.24 cm2 C.12π cm2 D.24π cm2
6.如图,AB为半圆O的直径,C,D是半圆O上的两点,∠BAC=20°,=,则∠DAC的度数是( )
A.40° B.35° C.30° D.25°
7.[2025滨州期末]如图,正六边形ABCDEF内接于⊙O,连接BF,OC,OD,则∠BFE-∠COD=( )
A.90° B.60° C.45° D.30°
8.如图,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,连接OE,OF,若∠C=90°,AC=3,BC=4,则阴影部分的面积为( )
A.2-π B.4-π C.4-π D.1-π
9.如图,在平面直角坐标系中,以5为半径的动圆的圆心A沿x轴移动,当⊙A与直线l:y=x只有一个公共点时,点A的坐标为( )
A.(-12,0) B.(-13,0) C.(±12,0) D.(±13,0)
10.[2025金华月考]如图,直线y=-x+6与坐标轴交于A,B两点,点C为坐标平面内一点,BC=2,点M为线段AC的中点,连接OM,则线段OM长度的最小值是( )
A.3+1 B.3-1 C.2 D.3
二、填空题(本大题共6 小题,每小题 4 分,共 24 分)
11.如图,AB为⊙O的直径,AB=1 cm,BC= cm,当AC=________cm时,直线AC与⊙O相切.
12.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,PO=8,则⊙O的半径OA等于______.
13.如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应的刻度值为64°,则∠BCD的度数为________.
14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.如图,点M表示筒车的一个盛水桶,当筒车工作时,盛水桶的运行路径是以轴心O(O在水面上方)为圆心的圆,且⊙O的半径(OA)为5米.若筒车工作时,盛水桶在水面以下的最大深度为2米,则这个圆被水面截得的弦AB的长为________米.
15.如图,四边形ABCD是⊙O的内接四边形,点O在四边形ABCD内部,过点C作⊙O的切线交AB的延长线于点P,连接OA,OB.若∠AOB=140°,∠BCP=35°,则∠ADC的度数为________.
16.如图,三条笔直的小路a,b,c相交围成一个三角形公园ABC,在△ABC的内心I处修建了一个凉亭,过凉亭的小路d∥c,并分别与△ABC的两边AB,AC相交于点D,E,DE=150 m,小路c与d之间相距60 m,如果从凉亭分别向小路a,b,c修建一条石板路,那么这三条石板路的长度之和最小为________m,若游客从B处出发,沿B→D→I→E→C的路线,到达C处,那么所走的这段路程长为________m.
三、解答题(本大题共7小题,共66分,各小题都必须写出解答过程)
17.(8分)如图,已知⊙O的两条弦AB,CD相交于点M,且AB=CD,连接AD.求证:AM=DM.
18.(8分)如图,在△ABC中,AC=AB,以AB为直径的⊙O分别交AC,BC于点D,E,连接OD.
(1)求证:CE=BE;
(2)若∠C=70°,求∠BOD的度数.
19.(8分)如图,在平面直角坐标系中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
(1)若△ABC的外接圆的圆心为M,则点M的坐标为________,⊙M的半径为________;
(2)△ABC的外接圆与x轴的另一个交点的坐标是________;
(3)求⊙M中的长.
20.(10分)如图①,已知圆锥的母线长l=16 cm,若以圆锥的顶点为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角为270°.
(1)求圆锥的底面半径r;
(2)求圆锥的全面积.
21.(10分)[2024南通中考]如图,在△ABC中,AB=3,AC=4,BC=5,⊙A与BC相切于点D.
(1)求图中阴影部分的面积;
(2)设⊙A上有一动点P,连接CP,BP.当CP的长最大时,求BP的长.
22.(10分)[2024自贡中考]在Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F.
(1)图①中三组相等的线段分别是CE=CF,AF=________,BD=________;若AC=3,BC=4,则⊙O半径长为________.
(2)如图②,延长AC到点M,使AM=AB,过点M作MN⊥AB于点N.求证:MN是⊙O的切线.
23.(12分)如图①,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E,F都在直线l上,且AB=7,EF=10,BC>5.点B以每秒1个单位长度的速度从点E处出发,沿射线EF的方向运动,矩形ABCD随之运动,运动时间为t秒.
(1)如图②,当t=2.5时,求半圆O在矩形ABCD内的弧的长度;
(2)在点B运动的过程中,当AD,BC都与半圆O相交时,设AD与半圆O交于点G,BC与半圆O交于点H.连接OG,OH,若∠GOH为直角,求此时t 的值.
答案
一、1.A 2.C 3.B 4.A 5.C 6.B 7.D 8.D 9.D 10.B
二、11.1 12.4 13.58° 14.8
15.105° 16.180;300
三、17.证明:∵AB=CD,∴=,
即+=+.
∴=.∴∠D=∠A.
∴AM=DM.
18.(1)证明:连接AE,
∵AB是⊙O的直径,∴∠AEB=90°.
∴AE⊥BC.又∵AB=AC,
∴E是BC的中点,∴CE=BE.
(2)解:∵AB=AC,
∴∠B=∠C=70°,
∴∠BAC=180°-∠B-∠C=40°.
∵∠BAC=∠BOD,∴∠BOD=80°.
19.解:(1)(5,5); (2)(7,0)
(3)连接MC,MA.
∵A(0,7),C(3,0),M(5,5),
∴AC==,MC=MA=.∴MC2+MA2=AC2.
∴△MAC是直角三角形,
且∠AMC=90°.
∴的长为=.
20.解:(1)由题意得3×2πr=,∴r=4 cm.
(2)圆锥的全面积为π×42+×2×4π×16=80π(cm2).
21.解:(1)如图,连接AD,
∵AB=3,AC=4,BC=5,
∴AB2+AC2=32+42=25=52=BC2,∴∠BAC=90°.
∵BC与⊙A相切于点D,∴AD⊥BC.
∴S△ABC=AD·BC=AC·AB,
∴AD===,
∴S阴影=S△ABC-S扇形=×3×4-=6-π.
(2)如图,当点P在CA的延长线上时,CP的长最大,由(1)知∠BAC=∠PAB=90°,AP=AD=,
∴PB==.
22.(1)AD;BE;1
(2)证明:如图,连接OD,OE,OF,OA,OM,ON,OC,OB,作OG⊥MN于点G,
设⊙O半径为r,
∵MN⊥AB,
∴∠ACB=∠ANM=90°.又∵∠CAB=∠NAM,AB=AM,
∴△CAB≌△NAM,
∴S△CAB=S△NAM,AN=AC,MN=BC.
∵⊙O是△ABC的内切圆,切点分别为D,E,F,∴OD=OE=OF=r,
∴S△ABC=(AC+BC+AB)·r,同理S△AMN=(AN+AM)·r+MN·OG,
∴(AC+BC+AB)·r=(AN+AM)·r+MN·OG,
∴OG=r,即OG为⊙O的半径.
又∵OG⊥MN,∴MN是⊙O的切线.
23.解:(1)设BC与半圆O交于点M,连接ME,MO.当t=2.5时,BE=2.5.
∵EF=10,∴OE=EF=5.
∴OB=2.5.∴EB=OB.
在矩形ABCD中,∠ABC=90°,
∴ME=MO.
又∵MO=EO,∴ME=EO=MO=5.
∴△MOE是等边三角形.∴∠EOM=60°.∴的长度为=,即半圆O在矩形ABCD内的弧的长度为.
(2)∵∠GOH=90°,
∴∠AOG+∠BOH=90°.
∵∠AGO+∠AOG=90°,
∴∠AGO=∠BOH.
在△AGO和△BOH中,
∴△AGO≌△BOH.∴OB=AG=t-5.∵AB=7,∴AE=t-7,
∴AO=5-(t-7)=12-t.
在Rt△AGO中,AG2+AO2=OG2,
∴(t-5)2+(12-t)2=52,
解得t1=8,t2=9,即t的值为8或9.
同课章节目录
