第二十二章 二次函数 学情评估卷(含答案)人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数 学情评估卷(含答案)人教版数学九年级上册 |  | |
| 格式 | doc | ||
| 文件大小 | 359.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 07:53:14 | ||
图片预览




文档简介
第二十二章 二次函数 学情评估卷
时间: 90分钟 满分: 120分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列y关于x的函数中,一定是二次函数的是( )
A.y=(a+2)x2+1 B.y=+1
C.y=(x+2)(x+1)-x2 D.y=2x2+3x
2.抛物线y=3x2-2x-1与y轴的交点坐标为( )
A.(0,1) B.(1,0) C.(0,-1) D.(-1,0)
3.已知二次函数y=(x-2)2+1,下列结论错误的是( )
A.其图象的开口向上 B.其图象与x轴没有交点
C.其图象的顶点坐标为(2,1) D.当x>1时,y随x的增大而增大
4.已知二次函数y=x2-2x-3,当-1≤x≤2时,函数的最大值为( )
A.-3 B.-1 C.0 D.2
5.将抛物线y=(x-2)2-4向右平移a个单位长度,再向上平移b个单位长度得到的图象对应的函数解析式为y=(x-3)2-7,则a,b的值分别是( )
A.1,-3 B.1,2 C.1,3 D.-2,-3
6.如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2-mx+c>n的解集为( )
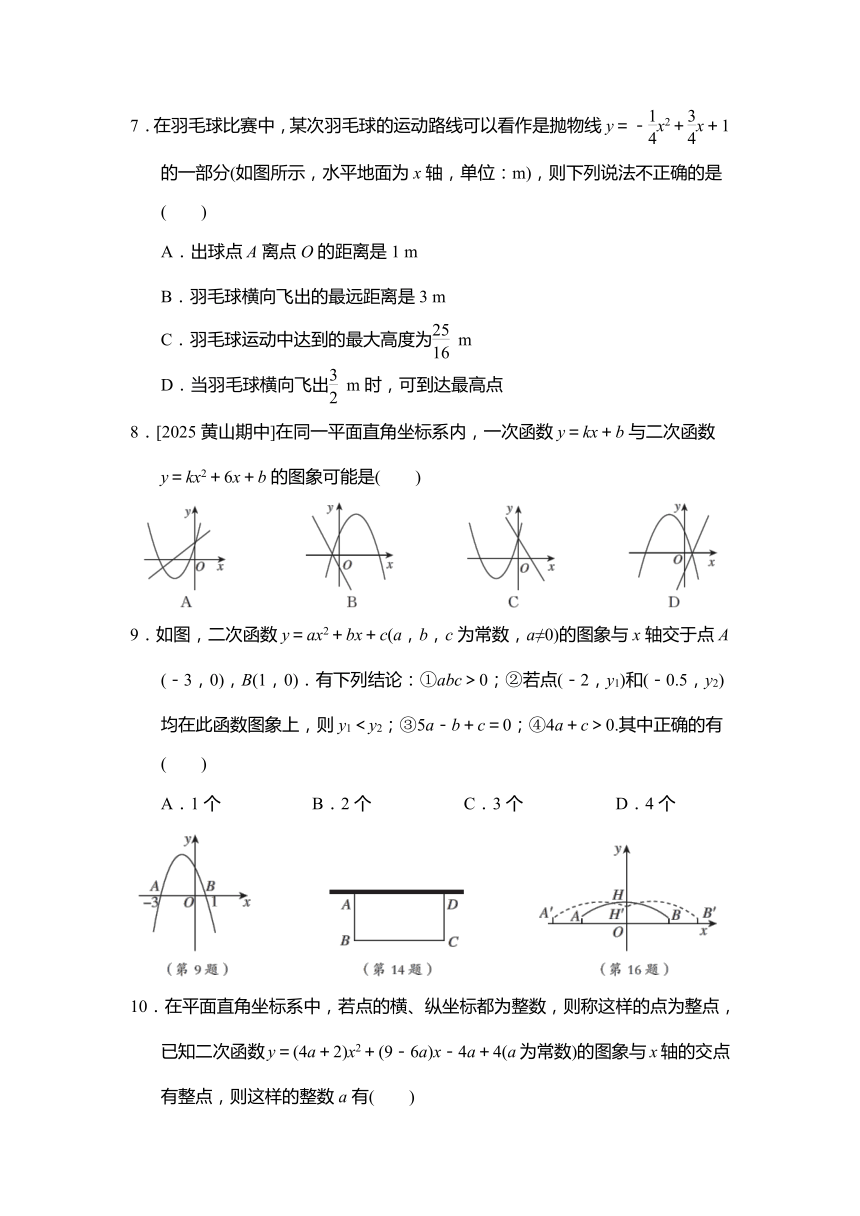
A.x>-1 B.x<3 C.x<-1或x>3 D.-17.在羽毛球比赛中,某次羽毛球的运动路线可以看作是抛物线y=-x2+x+1的一部分(如图所示,水平地面为x轴,单位:m),则下列说法不正确的是( )
A.出球点A离点O的距离是1 m
B.羽毛球横向飞出的最远距离是3 m
C.羽毛球运动中达到的最大高度为 m
D.当羽毛球横向飞出 m时,可到达最高点
8.[2025黄山期中]在同一平面直角坐标系内,一次函数y=kx+b与二次函数 y=kx2+6x+b的图象可能是( )
9.如图,二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与x轴交于点A (-3,0),B(1,0).有下列结论:①abc>0;②若点(-2,y1)和(-0.5,y2)均在此函数图象上,则y1<y2;③5a-b+c=0;④4a+c>0.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.在平面直角坐标系中,若点的横、纵坐标都为整数,则称这样的点为整点,已知二次函数y=(4a+2)x2+(9-6a)x-4a+4(a为常数)的图象与x轴的交点有整点,则这样的整数a有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,每小题4分,共24分)
11.请你写出一个二次函数:________,其图象满足条件:①开口向下;②图象过原点.
12.[2025北京西城区期中]已知点A(-1,y1),B(4,y2)在二次函数y=(x-2)2的图象上,y1与y2的大小关系为y1________y2(填“>”“<”或“=”).
13.一个二次函数的图象与y轴的交点到原点的距离为8,它的顶点坐标为(-1,2),那么它的解析式为________________.
14.如图,王叔叔想用长为60 m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知房屋外墙足够长,当矩形ABCD的边AB=________m时,羊圈的面积最大.
15.已知抛物线y=x2+kx-1经过(-2,n)和(4,n)两点,P为x轴上方抛物线上一点.若点P到对称轴的距离与点P到x轴的距离相等,则点P的纵坐标为________.
16.“过水门”仪式因两辆或两辆以上的消防车在飞机两侧喷射水雾时,会出现一个“水门”状的效果而得名.这一项仪式极具象征意义,寓意“接风洗尘”,是国际民航中高级别的礼仪.在一次“过水门”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图,当两辆消防车喷水口A,B的水平距离为80 m时,两条水柱在抛物线的顶点H处相遇.此时相遇点H距地面20 m,喷水口A,B距地面均为4 m.若两辆消防车同时后退10 m,两条水柱的形状及喷水口A′,B′到地面的距离均保持不变,则此时两条水柱相遇点H′距地面________m.
三、解答题(本大题共7小题,共66分,各小题都必须写出解答过程)
17.(8分)已知二次函数y=(2x+3)(1-x)-3.
(1)将该二次函数化为一般式,并分别写出其二次项、一次项和常数项;
(2)写出该二次函数图象的顶点坐标.
18. (8分)如图,二次函数y=(x-1)(x-a)(a为常数)的图象的对称轴为直线x=2.
(1)求a的值;
(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的解析式.
19.(8分)[2024扬州月考]如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(4,0),与y轴交于点C.
(1)求抛物线对应的函数解析式,并直接写出抛物线的顶点P的坐标;
(2)求△BCP的面积.
20.(10分)如图,直线y1=x-1和抛物线y2=x2+bx+c都经过点A(1,0),B (3,2).
(1)求抛物线的解析式;
(2)当1(3)当x为何值时不等式x2+bx+c>x-1成立?请你直接写出x的取值范围.
21.(10分)一次足球训练中,小明从球门正前方8 m的A处射门,球射向球门的路线呈抛物线状.当球飞行的水平距离为6 m时,球到达最高点,此时球离地面3 m.已知球门高OB为2.44 m,现以O为原点建立如图所示的直角坐标系.
(1)求抛物线的函数解析式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25 m处?
22.(10分)果园有果树60棵,现准备多种一些果树来提高产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内每棵果树的平均产量为75 kg.在确保每棵果树平均产量不低于40 kg的前提下,设增种果树x(x>0且x为整数)棵,该果园每棵果树的平均产量为y kg,它们之间的函数关系为一次函数关系,且满足如图所示的图象.
(1)图中点P所表示的实际意义是_______________________________________,每增种1棵果树时,每棵果树的平均产量减少________kg.
(2)求y关于x的函数解析式,并写出自变量的取值范围.
(3)当增种果树多少棵时,果园的总产量w(kg)最大?最大总产量是多少?
23.(12分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于B(4,0),C(-2,0)两点,与y轴交于点A(0,-2).
(1)求该抛物线的函数解析式;
(2)若点P是直线AB下方抛物线上的一动点,过点P作x轴的平行线交AB于点K,过点P作y轴的平行线交x轴于点D,求PK+PD的最大值及此时点P的坐标;
(3)在该抛物线的对称轴上是否存在一点M,使得△MAB是以AB为一条直角边的直角三角形?若存在,请求出点M的坐标,若不存在,请说明理由.
答案
一、1.D 2.C 3.D 4.C 5.A 6.C 7.B 8.A 9.C 10.C
二、11.y=-x2(答案不唯一) 12.>
13.y=6(x+1)2+2或y=-10(x+1)2+2
14.15 15.2 16.19
三、17.解:(1)y=(2x+3)(1-x)-3=-2x2-x.二次项为-2x2,一次项是-x,常数项是0.
(2)y=-2x2-x=-2+,则该二次函数图象的顶点坐标为.
18.解:(1)由二次函数y=(x-1)(x-a)(a为常数)知,其图象与x轴的交点坐标是(1,0)和(a,0).
∵对称轴为直线x=2,
∴=2,解得a=3.
(2)由(1)知a=3,则该二次函数的解析式是y=(x-1)(x-3),
即y=x2-4x+3.
∵平移后的图象经过原点,
∴平移后图象所对应的二次函数的解析式是y=x2-4x.
19.解:(1)∵抛物线y=x2+bx+c与x轴交于点A(-1,0),B(4,0),
∴解得
∴抛物线的解析式为y=x2-3x-4.顶点P的坐标为.
(2)连接OP,由y=x2-3x-4可知点C的坐标为(0,-4).
又∵B(4,0),P,
∴S△OPC=×4×=3,S△BOP=×4×=,S△BOC=×4×4=8,
∴S△BPC=S△OPC+S△BOP-S△BOC=3+-8=.
20.解:(1)∵抛物线 y2=x2+bx+c经过点A(1,0),B(3,2),
∴解得
∴抛物线的解析式为y2=x2-3x+2.
(2)-≤y2<2
(3)x的取值范围为x<1或x>3.
21.解:(1)易知抛物线的顶点坐标为(2,3).
∴设抛物线的函数解析式为 y=a(x-2)2+3,
把点A(8,0)的坐标代入,得36a+3=0,解得a=-,
∴抛物线的函数解析式为y=-(x-2)2+3.
当x=0时,y=-×4+3=>2.44,∴球不能射进球门.
(2)设小明应带球向正后方移动m m,则移动后的抛物线的解析式为y= -(x-2-m)2+3,把点(0,2.25)的坐标代入,得2.25=-×(0-2- m)2+3,解得 m=-5(舍去)或m=1,∴当时他应该带球向正后方移动1 m射门,才能让足球经过点O正上方2.25 m处.
22.解:(1)增种果树28棵时,每棵果树的平均产量为66 kg;
(2)设y关于x的函数解析式为y=kx+b.
把分别代入上式,得解得
∴y关于x的函数解析式为y=-x+80,自变量x的取值范围是0(3)w=(60+x)=-x2+50x+4 800.
∵-<0,∴当x=-=50 时,w最大值=6 050.
答:当增种果树50棵时,果园的总产量w(kg)最大,最大总产量是6 050 kg.
23.解:(1)根据题意得解得∴该抛物线的函数解析式为y=x2-x-2.
(2)∵A(0,-2),B(4,0),
∴直线AB的解析式为y=x-2,
设P(0<m<4),
则K,
∴PK+PD=(m-m2+m)+=-m2+m+2=-(m-)2+,
∵-<0,∴当m=时,PK+PD有最大值,此时P.
(3)存在.如图,过B作BM1⊥AB交抛物线的对称轴于点M1,过A作AM2⊥AB交抛物线的对称轴于点M2,连接AM1,BM2,由(1)易知抛物线的对称轴为直线x=1.
设M1(1,n),则AM12=n2+4n+5,BM12=n2+9,
由AB2+BM12=AM12,可得22+42+n2+9=n2+4n+5,解得n=6,
∴M1(1,6),∴直线 BM1的解析式为y=-2x+8.
∵AM2⊥AB,BM1⊥AB,
∴AM2∥BM1,
又∵直线AM2经过A(0,-2),
∴易得直线AM2的解析式为y=-2x-2,
∴当x=1时,y=-2×1-2=-4,
∴M2(1,-4).
综上所述,点M的坐标为(1,6)或(1,-4).
时间: 90分钟 满分: 120分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列y关于x的函数中,一定是二次函数的是( )
A.y=(a+2)x2+1 B.y=+1
C.y=(x+2)(x+1)-x2 D.y=2x2+3x
2.抛物线y=3x2-2x-1与y轴的交点坐标为( )
A.(0,1) B.(1,0) C.(0,-1) D.(-1,0)
3.已知二次函数y=(x-2)2+1,下列结论错误的是( )
A.其图象的开口向上 B.其图象与x轴没有交点
C.其图象的顶点坐标为(2,1) D.当x>1时,y随x的增大而增大
4.已知二次函数y=x2-2x-3,当-1≤x≤2时,函数的最大值为( )
A.-3 B.-1 C.0 D.2
5.将抛物线y=(x-2)2-4向右平移a个单位长度,再向上平移b个单位长度得到的图象对应的函数解析式为y=(x-3)2-7,则a,b的值分别是( )
A.1,-3 B.1,2 C.1,3 D.-2,-3
6.如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2-mx+c>n的解集为( )
A.x>-1 B.x<3 C.x<-1或x>3 D.-1
A.出球点A离点O的距离是1 m
B.羽毛球横向飞出的最远距离是3 m
C.羽毛球运动中达到的最大高度为 m
D.当羽毛球横向飞出 m时,可到达最高点
8.[2025黄山期中]在同一平面直角坐标系内,一次函数y=kx+b与二次函数 y=kx2+6x+b的图象可能是( )
9.如图,二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与x轴交于点A (-3,0),B(1,0).有下列结论:①abc>0;②若点(-2,y1)和(-0.5,y2)均在此函数图象上,则y1<y2;③5a-b+c=0;④4a+c>0.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.在平面直角坐标系中,若点的横、纵坐标都为整数,则称这样的点为整点,已知二次函数y=(4a+2)x2+(9-6a)x-4a+4(a为常数)的图象与x轴的交点有整点,则这样的整数a有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共6小题,每小题4分,共24分)
11.请你写出一个二次函数:________,其图象满足条件:①开口向下;②图象过原点.
12.[2025北京西城区期中]已知点A(-1,y1),B(4,y2)在二次函数y=(x-2)2的图象上,y1与y2的大小关系为y1________y2(填“>”“<”或“=”).
13.一个二次函数的图象与y轴的交点到原点的距离为8,它的顶点坐标为(-1,2),那么它的解析式为________________.
14.如图,王叔叔想用长为60 m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知房屋外墙足够长,当矩形ABCD的边AB=________m时,羊圈的面积最大.
15.已知抛物线y=x2+kx-1经过(-2,n)和(4,n)两点,P为x轴上方抛物线上一点.若点P到对称轴的距离与点P到x轴的距离相等,则点P的纵坐标为________.
16.“过水门”仪式因两辆或两辆以上的消防车在飞机两侧喷射水雾时,会出现一个“水门”状的效果而得名.这一项仪式极具象征意义,寓意“接风洗尘”,是国际民航中高级别的礼仪.在一次“过水门”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分.如图,当两辆消防车喷水口A,B的水平距离为80 m时,两条水柱在抛物线的顶点H处相遇.此时相遇点H距地面20 m,喷水口A,B距地面均为4 m.若两辆消防车同时后退10 m,两条水柱的形状及喷水口A′,B′到地面的距离均保持不变,则此时两条水柱相遇点H′距地面________m.
三、解答题(本大题共7小题,共66分,各小题都必须写出解答过程)
17.(8分)已知二次函数y=(2x+3)(1-x)-3.
(1)将该二次函数化为一般式,并分别写出其二次项、一次项和常数项;
(2)写出该二次函数图象的顶点坐标.
18. (8分)如图,二次函数y=(x-1)(x-a)(a为常数)的图象的对称轴为直线x=2.
(1)求a的值;
(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的解析式.
19.(8分)[2024扬州月考]如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(4,0),与y轴交于点C.
(1)求抛物线对应的函数解析式,并直接写出抛物线的顶点P的坐标;
(2)求△BCP的面积.
20.(10分)如图,直线y1=x-1和抛物线y2=x2+bx+c都经过点A(1,0),B (3,2).
(1)求抛物线的解析式;
(2)当1
21.(10分)一次足球训练中,小明从球门正前方8 m的A处射门,球射向球门的路线呈抛物线状.当球飞行的水平距离为6 m时,球到达最高点,此时球离地面3 m.已知球门高OB为2.44 m,现以O为原点建立如图所示的直角坐标系.
(1)求抛物线的函数解析式,并通过计算判断球能否射进球门(忽略其他因素);
(2)对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点O正上方2.25 m处?
22.(10分)果园有果树60棵,现准备多种一些果树来提高产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内每棵果树的平均产量为75 kg.在确保每棵果树平均产量不低于40 kg的前提下,设增种果树x(x>0且x为整数)棵,该果园每棵果树的平均产量为y kg,它们之间的函数关系为一次函数关系,且满足如图所示的图象.
(1)图中点P所表示的实际意义是_______________________________________,每增种1棵果树时,每棵果树的平均产量减少________kg.
(2)求y关于x的函数解析式,并写出自变量的取值范围.
(3)当增种果树多少棵时,果园的总产量w(kg)最大?最大总产量是多少?
23.(12分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于B(4,0),C(-2,0)两点,与y轴交于点A(0,-2).
(1)求该抛物线的函数解析式;
(2)若点P是直线AB下方抛物线上的一动点,过点P作x轴的平行线交AB于点K,过点P作y轴的平行线交x轴于点D,求PK+PD的最大值及此时点P的坐标;
(3)在该抛物线的对称轴上是否存在一点M,使得△MAB是以AB为一条直角边的直角三角形?若存在,请求出点M的坐标,若不存在,请说明理由.
答案
一、1.D 2.C 3.D 4.C 5.A 6.C 7.B 8.A 9.C 10.C
二、11.y=-x2(答案不唯一) 12.>
13.y=6(x+1)2+2或y=-10(x+1)2+2
14.15 15.2 16.19
三、17.解:(1)y=(2x+3)(1-x)-3=-2x2-x.二次项为-2x2,一次项是-x,常数项是0.
(2)y=-2x2-x=-2+,则该二次函数图象的顶点坐标为.
18.解:(1)由二次函数y=(x-1)(x-a)(a为常数)知,其图象与x轴的交点坐标是(1,0)和(a,0).
∵对称轴为直线x=2,
∴=2,解得a=3.
(2)由(1)知a=3,则该二次函数的解析式是y=(x-1)(x-3),
即y=x2-4x+3.
∵平移后的图象经过原点,
∴平移后图象所对应的二次函数的解析式是y=x2-4x.
19.解:(1)∵抛物线y=x2+bx+c与x轴交于点A(-1,0),B(4,0),
∴解得
∴抛物线的解析式为y=x2-3x-4.顶点P的坐标为.
(2)连接OP,由y=x2-3x-4可知点C的坐标为(0,-4).
又∵B(4,0),P,
∴S△OPC=×4×=3,S△BOP=×4×=,S△BOC=×4×4=8,
∴S△BPC=S△OPC+S△BOP-S△BOC=3+-8=.
20.解:(1)∵抛物线 y2=x2+bx+c经过点A(1,0),B(3,2),
∴解得
∴抛物线的解析式为y2=x2-3x+2.
(2)-≤y2<2
(3)x的取值范围为x<1或x>3.
21.解:(1)易知抛物线的顶点坐标为(2,3).
∴设抛物线的函数解析式为 y=a(x-2)2+3,
把点A(8,0)的坐标代入,得36a+3=0,解得a=-,
∴抛物线的函数解析式为y=-(x-2)2+3.
当x=0时,y=-×4+3=>2.44,∴球不能射进球门.
(2)设小明应带球向正后方移动m m,则移动后的抛物线的解析式为y= -(x-2-m)2+3,把点(0,2.25)的坐标代入,得2.25=-×(0-2- m)2+3,解得 m=-5(舍去)或m=1,∴当时他应该带球向正后方移动1 m射门,才能让足球经过点O正上方2.25 m处.
22.解:(1)增种果树28棵时,每棵果树的平均产量为66 kg;
(2)设y关于x的函数解析式为y=kx+b.
把分别代入上式,得解得
∴y关于x的函数解析式为y=-x+80,自变量x的取值范围是0
∵-<0,∴当x=-=50 时,w最大值=6 050.
答:当增种果树50棵时,果园的总产量w(kg)最大,最大总产量是6 050 kg.
23.解:(1)根据题意得解得∴该抛物线的函数解析式为y=x2-x-2.
(2)∵A(0,-2),B(4,0),
∴直线AB的解析式为y=x-2,
设P(0<m<4),
则K,
∴PK+PD=(m-m2+m)+=-m2+m+2=-(m-)2+,
∵-<0,∴当m=时,PK+PD有最大值,此时P.
(3)存在.如图,过B作BM1⊥AB交抛物线的对称轴于点M1,过A作AM2⊥AB交抛物线的对称轴于点M2,连接AM1,BM2,由(1)易知抛物线的对称轴为直线x=1.
设M1(1,n),则AM12=n2+4n+5,BM12=n2+9,
由AB2+BM12=AM12,可得22+42+n2+9=n2+4n+5,解得n=6,
∴M1(1,6),∴直线 BM1的解析式为y=-2x+8.
∵AM2⊥AB,BM1⊥AB,
∴AM2∥BM1,
又∵直线AM2经过A(0,-2),
∴易得直线AM2的解析式为y=-2x-2,
∴当x=1时,y=-2×1-2=-4,
∴M2(1,-4).
综上所述,点M的坐标为(1,6)或(1,-4).
同课章节目录
