4.1 因式分解 课件(共25张PPT)
文档属性
| 名称 | 4.1 因式分解 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 09:09:15 | ||
图片预览








文档简介
(共25张PPT)
4.1 因式分解
第四章 因式分解
北师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1. 理解掌握因式分解的意义,会判断一个变形是否为因式分解.
2. 理解因式分解与整式乘法之间的联系与区别.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 630可以被哪些整数整除?
导入新知
思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
解决这个问题,需要对630进行分解质因数
(1)单项式×单项式: .
(2)单项式×多项式: .
(3)多项式×多项式: .
2.整式乘法类型
导入新知
(1)平方差公式: (() = .
(2)完全平方公式: (a±b)2= .
3.特殊的整式乘法公式
a2±2ab+b2
a2-b2
1.能被100整除吗?
探究新知
知识点 1
因式分解的定义
小明是这样做的:
.
所以,能被100整除.
你知道每一步的依据吗?
.
所以,能被100整除.
还能被哪些正整数整除?
还能被98,99整除
探究新知
在这里,解决问题的关键是把一个数式
化成了几个数的积的形式.
2.将99换成其他任意一个大于1的整数,上述结论仍然成立吗
探究新知
用a表示任意一个大于1的整数,则:
上面的式子化成了几个整式乘积的形式.
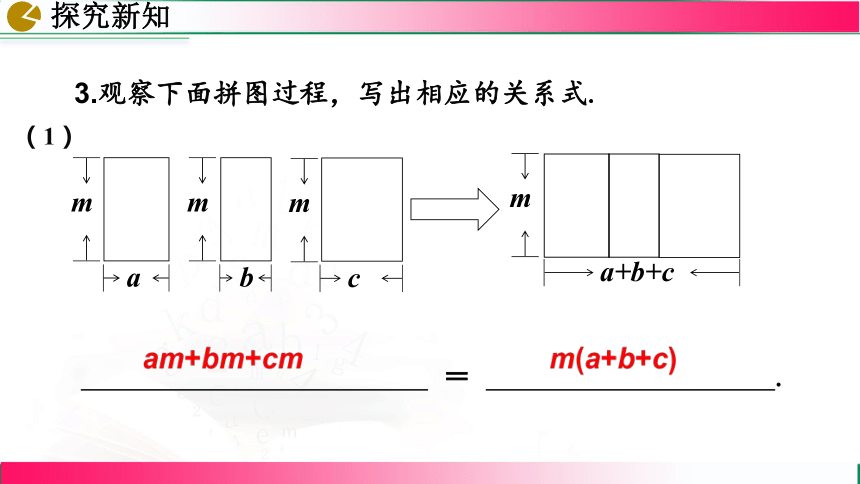
3.观察下面拼图过程,写出相应的关系式.
(1)
探究新知
m
m
m
m
a
b
c
a+b+c
= .
3.观察下面拼图过程,写出相应的关系式.
(2)
探究新知
x
x
x+1
1
x+1
= .
x
x
1
1
1
4.大家观察,这几个式子的变形有什么特点?
,
,
.
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.也可称为分解因式.
①分解的对象必须是多项式;
②分解的结果一定是几个整式的乘积的形式,且每个因式的次数不能高于原来多项式的次数;
③必须分解到每个多项式都不能再分解为止.
结论
探究新知
注意:
例1
探究新知
解:
∴ 能被45整除.
利用因式分解判断能否整除
素养考点 1
A.
B.
C.
D.
B
探究新知
下列各式从左到右的变形中,是分解因式的是( )
例2
考查因式分解的概念
素养考点 2
判断下列等式从左到右的变形是否为因式分解?
(1)
(2)
(3)
(4)
(5)
不是
不是
不是
不是
巩固练习
变式训练
不是
完成下列题目:
.
.
.
探究新知
知识点 2
因式分解与整式乘法的关系
根据左面算式,解决下列问题:
.
.
.
观察同一行中,左右两边的等式有什么区别和联系?
探究新知
联系:左右两式是同一多项式的不同表现形式.
区别:左边一栏是整式乘法,右边一栏是因式分解,
他们的运算是相反的.
想一想:整式乘法与因式分解有什么关系?
整式乘法
因式分解
是互逆的恒等变形,即
例 (1)若多项式分解因式的结果为
,则的值为 .
(2)若,则 ,
.
探究新知
-3
因式分解与整式乘法的关系的应用
素养考点 3
1.母题教材P93随堂练习 下列各式从左到右的变形中,属
于因式分解的是( )
A
A.
B.
C.
D.
2.[2024保定竞秀区期中] 若多项式 因式分解后有
一个因式是,则 ____.
返回
3. 一个图形通过
两种不同的方法计算它的面积或
体积,可以得到一个数学等式.如
图,将一个边长为 的正方形纸
片剪去一个边长为 的小正方形,根据剩下部分的面积和重
新拼成的长方形的面积,可得一个关于, 的等式:______
_______________________.
返回
4.如果,求 的值.
【解】 ,则
, .
.
返回
5.已知多项式 能分解为两个整系数的一次式的乘
积,则 的值有( )
A
A.10个 B.8个 C.5个 D.4个
6.如果把多项式因式分解得 ,那
么 ____.
返回
7. 两名同学将一个二次三项式分解因式,一
名同学因看错了一次项系数而分解成 ,另一名
同学因看错了常数项而分解成 ,求出原多项式.
【解】设原多项式为.(其中,, 均为常数,且
)
,
由题意得, .
又 ,
由题意得 .
原多项式为 .
返回
因式分解
定 义
与整式乘法运算的关系
把一个多项式化成几个整式的乘积的形式,叫做因式分解,也可称为分解因式.
课堂小结
因式分解
整式乘法
多项式化为整式乘积
因式分解与整式乘法是互逆的恒等变形.
整式乘积化为多项式
谢谢观看!
4.1 因式分解
第四章 因式分解
北师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
1. 理解掌握因式分解的意义,会判断一个变形是否为因式分解.
2. 理解因式分解与整式乘法之间的联系与区别.
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 630可以被哪些整数整除?
导入新知
思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
解决这个问题,需要对630进行分解质因数
(1)单项式×单项式: .
(2)单项式×多项式: .
(3)多项式×多项式: .
2.整式乘法类型
导入新知
(1)平方差公式: (() = .
(2)完全平方公式: (a±b)2= .
3.特殊的整式乘法公式
a2±2ab+b2
a2-b2
1.能被100整除吗?
探究新知
知识点 1
因式分解的定义
小明是这样做的:
.
所以,能被100整除.
你知道每一步的依据吗?
.
所以,能被100整除.
还能被哪些正整数整除?
还能被98,99整除
探究新知
在这里,解决问题的关键是把一个数式
化成了几个数的积的形式.
2.将99换成其他任意一个大于1的整数,上述结论仍然成立吗
探究新知
用a表示任意一个大于1的整数,则:
上面的式子化成了几个整式乘积的形式.
3.观察下面拼图过程,写出相应的关系式.
(1)
探究新知
m
m
m
m
a
b
c
a+b+c
= .
3.观察下面拼图过程,写出相应的关系式.
(2)
探究新知
x
x
x+1
1
x+1
= .
x
x
1
1
1
4.大家观察,这几个式子的变形有什么特点?
,
,
.
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.也可称为分解因式.
①分解的对象必须是多项式;
②分解的结果一定是几个整式的乘积的形式,且每个因式的次数不能高于原来多项式的次数;
③必须分解到每个多项式都不能再分解为止.
结论
探究新知
注意:
例1
探究新知
解:
∴ 能被45整除.
利用因式分解判断能否整除
素养考点 1
A.
B.
C.
D.
B
探究新知
下列各式从左到右的变形中,是分解因式的是( )
例2
考查因式分解的概念
素养考点 2
判断下列等式从左到右的变形是否为因式分解?
(1)
(2)
(3)
(4)
(5)
不是
不是
不是
不是
巩固练习
变式训练
不是
完成下列题目:
.
.
.
探究新知
知识点 2
因式分解与整式乘法的关系
根据左面算式,解决下列问题:
.
.
.
观察同一行中,左右两边的等式有什么区别和联系?
探究新知
联系:左右两式是同一多项式的不同表现形式.
区别:左边一栏是整式乘法,右边一栏是因式分解,
他们的运算是相反的.
想一想:整式乘法与因式分解有什么关系?
整式乘法
因式分解
是互逆的恒等变形,即
例 (1)若多项式分解因式的结果为
,则的值为 .
(2)若,则 ,
.
探究新知
-3
因式分解与整式乘法的关系的应用
素养考点 3
1.母题教材P93随堂练习 下列各式从左到右的变形中,属
于因式分解的是( )
A
A.
B.
C.
D.
2.[2024保定竞秀区期中] 若多项式 因式分解后有
一个因式是,则 ____.
返回
3. 一个图形通过
两种不同的方法计算它的面积或
体积,可以得到一个数学等式.如
图,将一个边长为 的正方形纸
片剪去一个边长为 的小正方形,根据剩下部分的面积和重
新拼成的长方形的面积,可得一个关于, 的等式:______
_______________________.
返回
4.如果,求 的值.
【解】 ,则
, .
.
返回
5.已知多项式 能分解为两个整系数的一次式的乘
积,则 的值有( )
A
A.10个 B.8个 C.5个 D.4个
6.如果把多项式因式分解得 ,那
么 ____.
返回
7. 两名同学将一个二次三项式分解因式,一
名同学因看错了一次项系数而分解成 ,另一名
同学因看错了常数项而分解成 ,求出原多项式.
【解】设原多项式为.(其中,, 均为常数,且
)
,
由题意得, .
又 ,
由题意得 .
原多项式为 .
返回
因式分解
定 义
与整式乘法运算的关系
把一个多项式化成几个整式的乘积的形式,叫做因式分解,也可称为分解因式.
课堂小结
因式分解
整式乘法
多项式化为整式乘积
因式分解与整式乘法是互逆的恒等变形.
整式乘积化为多项式
谢谢观看!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
