2.7 正方形 课件（共49张PPT）

(共49张PPT)
2.7 正方形
第2章 四边形
湘教版数学8年级下册（公开课课件）
授课教师：********
班 级：********
时 间：********
学生能够理解多边形、多边形的边、顶点、内角、外角等基本概念。
掌握多边形内角和公式与外角和定理，并能熟练运用它们进行相关计算。
学会判断一个多边形是否为凸多边形，以及理解正多边形的概念。
过程与方法目标
通过观察、测量、剪拼、推理等活动，培养学生的自主探究能力与逻辑推理能力。
经历多边形内角和公式的推导过程，体会从特殊到一般以及转化的数学思想方法。
情感态度与价值观目标
让学生在探索多边形知识的过程中，体验成功的喜悦，激发学习数学的兴趣。
培养学生的合作交流意识，提高团队协作能力。
二、教学重难点
重点
多边形的相关概念，包括边、顶点、内角、外角等。
多边形内角和公式与外角和定理的推导及应用。
难点
多边形内角和公式的推导过程，如何引导学生将多边形问题转化为三角形问题。
灵活运用多边形内角和公式与外角和定理解决实际问题。
三、教学方法
讲授法：系统地讲解多边形的基本概念、内角和公式与外角和定理，确保学生掌握基础知识。
探究法：组织学生进行探究活动，如测量多边形内角和、剪拼多边形等，让学生在实践中发现规律，培养探究能力。
小组合作法：安排学生分组讨论多边形内角和公式的推导方法、解决复杂问题等，促进学生之间的交流与合作。
练习法：通过针对性的练习题，巩固学生所学知识，提高学生的解题能力和应用能力。
四、教学过程
（一）导入新课（5 分钟）
展示生活中常见的多边形图片，如六边形的螺母、五边形的花坛、四边形的窗户等。
提问：同学们，在这些图片中，你们能发现哪些熟悉的图形？引导学生观察图形的边和角的特征，从而引出多边形的概念。
（二）知识讲解（20 分钟）
多边形的基本概念
定义：在平面内，由一些线段首尾顺次相接组成的封闭图形叫做多边形。
介绍多边形的边、顶点、内角、外角等概念，并结合图形进行说明。例如，在一个四边形 ABCD 中，线段 AB、BC、CD、DA 是它的边，点 A、B、C、D 是它的顶点，∠A、∠B、∠C、∠D 是它的内角，与内角∠A 相邻的外角为∠BAE。
凸多边形与凹多边形：通过展示凸多边形和凹多边形的图片，让学生观察它们的区别，从而给出凸多边形的定义：如果整个多边形都在任何一条边所在直线的同一侧，那么这个多边形就是凸多边形。
正多边形：给出正多边形的定义，各个角都相等，各条边都相等的多边形叫做正多边形，如正三角形、正方形、正六边形等
学习目标
1.探索并证明正方形的性质，并了解平行四边形、
矩形、菱形之间的联系和区别；(重点、难点)
2．探索并证明正方形的判定，并了解平行四边形、
矩形、菱形之间的联系和区别；(重点、难点)
3．会运用正方形的性质及判定条件进行有关的论证
和计算 . (难点)
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
观察下面图形,正方形是我们熟悉的几何图形，在生活中无处不在.
情景引入
你还能举出其他的例子吗？
矩 形
〃
〃
问题1：矩形怎样变化后就成了正方形呢 你有什么
发现？
问题引入
正方形的性质
一
正方形
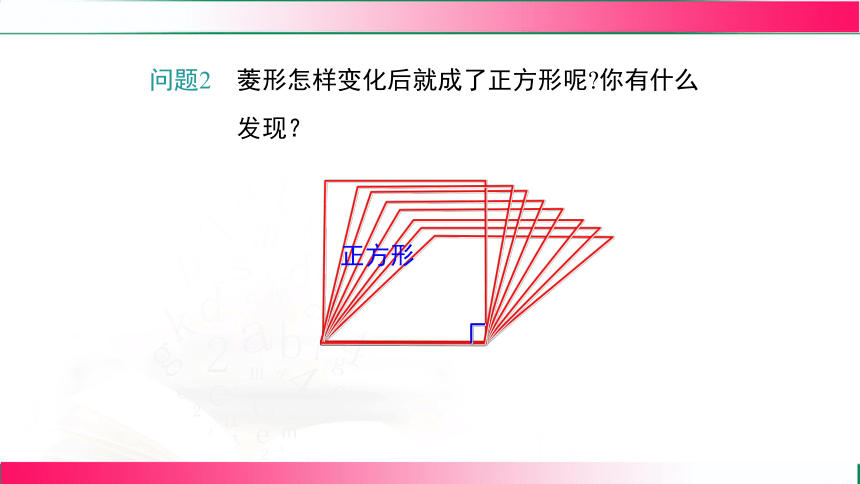
问题2 菱形怎样变化后就成了正方形呢 你有什么
发现？
正方形
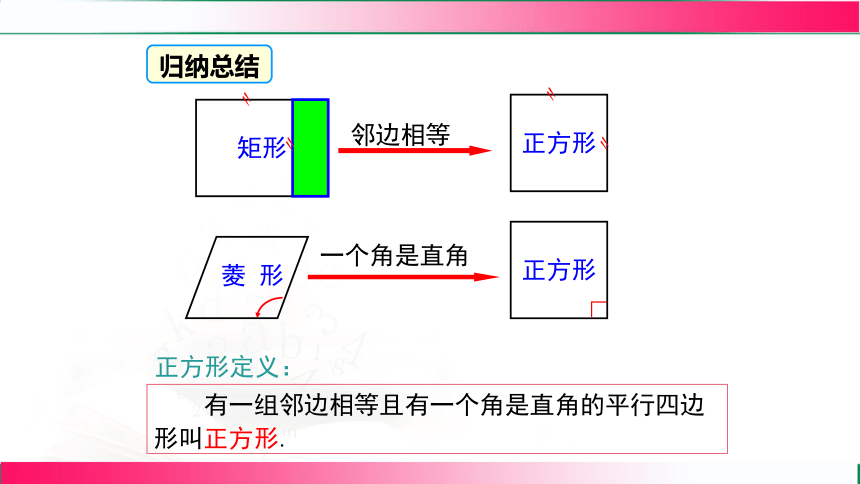
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形定义：
有一组邻边相等且有一个角是直角的平行四边形叫正方形.
归纳总结
已知：如图,四边形ABCD是正方形.
求证：正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明：∵四边形ABCD是正方形.
∴∠A=90°, AB=AD （正方形的定义）.
又∵正方形是平行四边形.
∴正方形是矩形（矩形的定义）,
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
证一证
已知：如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证：AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明：∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
矩形
菱形
正
方
形
平行四边形
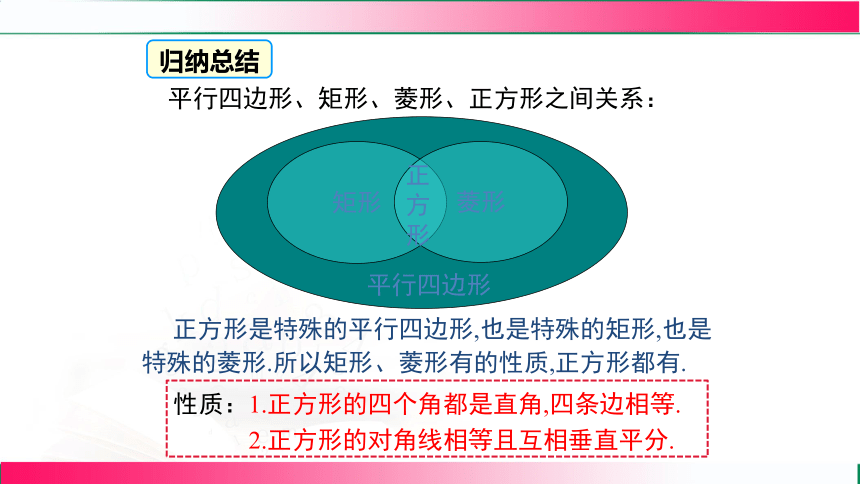
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系：
性质：1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
归纳总结
正方形是中心对称图形，对角线的交点是它的对称中心.
正方形是轴对称图形，两条对角线所在直线，以及过每一组对边中点的直线都是它的对称轴.
由于正方形既是菱形，又是矩形，因此：
知识要点
A
B
C
D
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知: 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的
等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
典例精析
例2 如图，在正方形ABCD中， ΔBEC是等边三角形，
求证： ∠EAD＝∠EDA＝15° .
证明：∵ ΔBEC是等边三角形，
∴BE=CE=BC,∠EBC=∠ECB=60°，
∵ 四边形ABCD是正方形，
∴AB=BC=CD,∠ABC=∠DCB=90°，
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°，
∴△ABE，△DCE是等腰三角形，
∴∠BAE =∠CDE =75°，
∴∠EAD= ∠EDA=90°-75°=15°.
例3 如图，在正方形ABCD中，P为BD上一点，PE⊥BC于E， PF⊥DC于F.试说明：AP=EF.
A
B
C
D
P
E
F
解:
连接PC，AC.
又∵PE⊥BC ， PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°, BD垂直平分AC,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
在正方形的条件下证明两条线段相等：通常连接对角线构造垂直平分的模型，利用垂直平分线性质，角平分线性质，等腰三角形等来说明.
归纳
正方形的判定
二
活动1 准备一张矩形的纸片，按照下图折叠,然后展开，折叠部分得到一个正方形，可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形？
矩形
正方形
一组邻边相等
对角线互相垂直
已知：如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证：四边形ABCD是正方形.
证明：∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ，∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线互相垂直的矩形是正方形.
活动2 把可以活动的菱形框架的一个角变为直角，观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形？
正方形
一个角是直角
对角线相等
已知：如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证：四边形ABCD是正方形.
证明：∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形，
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线相等的菱形是正方形.
正方形判定的几条途径：
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角，
一组邻边相等，
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等
一内角是直角
例4 在正方形ABCD中，点E、F、M、N分别在各边上，且AE=BF=CM=DN．四边形EFMN是正方形吗 为什么
证明：∵四边形ABCD是正方形，
∴AB=BC=CD=DA，∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN，
∴AN=BE=CF=DM.
分析：由已知可证△AEN≌△BFE≌
△CMF≌△DNM，得四边形EFMN是菱形，再证有一个角是直角即可.
在△AEN、△BFE、△CMF、△DNM中，
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM，∠ANE=∠BEF,
∴四边形EFMN是菱形，
∠NEF=180°－（∠AEN+∠BEF）
=180°－（∠AEN+∠ANE）
=180°－90°=90°.
∴四边形EFMN是正方形 .
证明：∵ DE⊥AC，DF⊥AB ，
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °，
∴四边形EDFC是矩形.
过点D作DG⊥AB，垂足为G.
∵AD是∠CAB的平分线
DE⊥AC，DG⊥AB，
∴ DE=DG.
同理得DG=DF，
∴ED=DF，
∴四边形EDFC是正方形.
例5 如图，在直角三角形中，∠C=90°，∠A、∠B的平分线交于点D.DE⊥AC，DF⊥BC.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
例6 如图，EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证：四边形EFGH是正方形.
证明：∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO =45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO ≌△BEO,∴OE=OH.
同理可证：OE=OF=OG,
B
A
C
D
O
E
H
G
F
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO ,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
D
O
E
H
G
F
例7 如图，正方形ABCD，动点E在AC上，AF⊥AC，垂足为A，AF=AE．
（1）求证：BF=DE；
（2）当点E运动到AC中点时(其他条件都保持不变)，
问四边形AFBE是什么特殊四边形？说明理由．
（1）证明：∵正方形ABCD，
∴AB=AD，∠BAD=90°，
∵AF⊥AC，∴∠EAF=90°，
∴∠BAF=∠EAD，
在△ADE和△ABF中，
AD＝AB ，∠DAE＝∠BAF ，AE＝AF ,
∴△ADE≌△ABF（SAS），∴BF=DE；
（2）解：当点E运动到AC的中点时四边形AFBE是正方形，
理由：∵点E运动到AC的中点，AB=BC，
∴BE⊥AC，BE=AE= AC，
∵AF=AE，
∴BE=AF=AE.
又∵BE⊥AC，∴∠FAE=∠BEC=90°，
∴BE∥AF，
∵BE=AF，
∴得平行四边形AFBE，
∵∠FAE=90°，AF=AE，
∴四边形AFBE是正方形．
思考 前面学菱形时我们探究了顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形各边中点能得到菱形，那么顺次连接正方形各边中点能得到怎样的特殊平行四边形？
A
B
C
D
A
B
C
D
A
B
C
D
矩形
正方形
任意四边形
平行四边形
菱形
正方形
E
F
G
H
E
F
G
H
E
F
G
H
装修房子铺地板的砖（如下图）大都是正方形的形状，它是什么样的四边形呢？它与平行四边形、矩形、菱形有什么关系？矩形呢？
图2-57
合作探究
我们把有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
平行四边形
菱形
正方形
矩形
图2-58
正方形的四条边都
相等，四个角都是直角.
正方形既是矩形又是菱形.
结论
正方形的四条边都相等，四个角都是直角.
正方形的对角线相等，且互相垂直平分.
可以知道：
正方形是中心对称图形，对角线的交点是它的对称中心.
正方形是轴对称图形，两条对角线所在直线，以及过每一组对边中点的直线都是它的对称轴.
由于正方形既是菱形，又是矩形，因此：
结论
如图2-59，点E是正方形ABCD的边AB上任意一点，过点D作DF⊥DE交BC的延长线于点F.
求证：DE = DF.
举
例
例1
∴ AD = CD， ∠A =∠DCF = 90°.
证明
∵ 四边形ABCD为正方形，
∵ DF⊥DE，
∴ ∠EDF = 90°， 即∠1 +∠3 = 90°，
图2-59
又 ∵ ∠2 +∠3 = 90°，
∴ ∠1 =∠2.
∴ △AED≌△CFD （ASA）.
∴ DE = DF.
图2-59
观察示意图2-58，说一说如何判断一个四边形是正方形？
可以先判定四边形是矩形，再判定这个矩形有一组邻边相等.
也可以先判定四边形是菱
形，再判定这个菱形有一
个角是直角.
举
例
例2
如图2-60， 已知点A′，B′， C′， D′分别是正方形ABCD 四条边上的点， 并且AA′= BB′= CC′= DD′.
求证：四边形 是正方形.
图2-60
证明
∵ 四边形ABCD为正方形，
∴ AB = BC = CD = DA.
又∵ AA′ = BB′ = CC′ = DD′，
∴ D′A = A′B = B′C = C′D.
又∵ ∠A =∠B =∠C =∠D = 90°，
∴ △AA′D′≌△BB′A′
≌△CC′B′≌△DD′C′.
图2-60
∴ A′D′= B′A′= C′B′= D′C′.
∴ 四边形 是菱形.
又∵ ∠1 =∠3， ∠1 +∠2 = 90°，
∴ ∠2 +∠3 = 90°.
∴ ∠D′A′B′= 90°.
∴ 四边形 是正方形.
图2-60
1. 正方形具备而菱形不具备的性质是( )
C
A. 对角线互相平分
B. 对角线互相垂直
C. 对角线相等
D. 每条对角线平分一组对角
返回
（第2题）
2. 如图,四边形是正方形,延长 到
点,使,则 的大小是( )
B
A. B.
C. D.
返回
（第3题）
3. [2024湖南师大附中月考] 如图， 是正方形
内位于对角线下方的一点， ，
则 的度数为( )
A
A. B. C. D.
4.[2024岳阳期中] 正方形的对角线长为8，则面积为____.
32
返回
5.在学校科技节活动中，聪聪用四根长度相同的木条制作了
能够活动的菱形学具.他先活动学具成为图①所示菱形，并测
得 ，接着活动学具成为图②所示正方形，并测得
对角线，则图①中对角线 的长为_____.
返回
6.[2024怀化二模] 如图，在中，点， 分别在边
，上，且四边形 是正方形.
（1）求证： ；
【证明】 四边形 是平行四边形，
，， .
四边形 是正方形，
.
在和中，
.
（2）已知的面积为20，，则 的长为___.
1
【点拨】 的面积为20，
， ，
， .
四边形 是正方形，
.
.
返回
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形.
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
谢谢观看！